高速铁路封闭式声屏障的风压荷载试验研究
敬海泉,彭天微,何旭辉,周继超,张世峰,张海瑜
(1. 中南大学 土木工程学院,湖南 长沙410075;2. 中南大学 高速铁路建造技术国家工程实验室,湖南 长沙410075;3. 中国铁路设计集团有限公司,天津300308)
声屏障是经济实效的降噪措施,在高速铁路领域得到了广泛应用[1]。我国部分规划及新建高铁,为降低特殊敏感点的噪声,已开始采用封闭式声屏障[2]。封闭式声屏障结构外形与隧道结构类似,列车经过时产生列车风效应。因此,封闭式声屏障在服役过程中受到列车风和横风共同作用,可能发生结构破坏并影响高铁行车安全。已有学者对声屏障的风压荷载进行了研究。郑史雄等[3]对直立式声屏障展开分析,获得了风荷载体型系数。XIONG 等[4−5]研究高速列车经过声屏障而产生的瞬态空气动力压力与压力变化,得出压力幅值沿声屏障表面的分布规律。DU 等[6]研究了列车速度与声屏障高度对声屏障所受到的压力幅值的影响。韩旭等[7]系统分析了风速、雷诺数效应、风攻角、侧视断面位置等因素对全封闭声屏障气动特性的影响。何旭辉等[8]对高速铁路全封闭声屏障气压荷载数值模拟研究,获得压力极值和气压荷载分布规律。朱正清等[9]通过对列车驶过声屏障时气动力模拟和试验测试,验证了声屏障压力波与速度、声屏障高度和屏轨距的关系。王宏朝等[10]通过数值模拟分析在不同的风向角及风速下,自然风荷载对声屏障所受列车风致脉动力的影响。目前高速铁路声屏障的风荷载研究已取得很大进展,但研究对象多为直立式声屏障。封闭式声屏障大多设置在路堤或桥梁段,与隧道环境差异较大,列车通过隧道的气动特性不完全适用于封闭式声屏障。本文以京雄城际铁路桥梁段封闭式声屏障作为研究对象,通过横风−移动列车风洞试验,研究了列车风与横风作用对声屏障结构的风压荷载影响规律,研究结果对高速铁路全封闭式声屏障结构设计具有指导意义。
1 风洞试验
中南大学风工程研究中心基于既有风洞实验室,研制了一套横风-移动列车风洞试验系统,可用于移动列车的气动特性、移动车-桥系统风荷载风洞试验。整套装置测试段位于中南大学高速铁路风洞大试验段内,来流区域宽12.0 m,高3.5 m,风速0~20 m/s 连续可调,紊流度低于1.0%;在风洞试验段的两端分别为上下行列车模型的弹射与减速设备,模型运行轨道贯通风洞测试段,来流风向与列车行驶方向垂直。
1.1 试验模型
列车、桥梁和封闭式声屏障均采用1:15 的缩尺比例制作几何缩尺模型,列车车型为CRH380A高速列车,桥梁为单箱梁,桥墩高度按照实际情况缩尺。如图1 所示,封闭式声屏障截面为圆弧形,桥梁模型贯穿整个风洞长12 m,为降低风洞试验阻塞率,声屏障模型长度取8 m。在声屏障两端,中间以及1/4 长度处共设置4 个测试截面,两端截面距离声屏障实际出入口0.5 m。

图1 试验模型Fig.1 Test model
测点布置如图2所示,每个截面的内外壁面均等距布设20个测点,试验不考虑近地面的风剖面,来流横风为均匀流。通过电子扫描阀测量声屏障内外壁的风压分布,试验中采用最长测管为1.2 m。

图2 封闭式声屏障测点布置图Fig.2 Test points of closed sound barrier
1.2 动模型弹射系统
中南大学高速铁路风洞列车模型弹射系统[11]如图3所示。弹射系统在风洞外的加速段利用电机同步带传动机构将列车模型加速至设定速度,接近风洞壁面时将列车模型弹出,列车模型沿轨道进入风洞试验段,当列车模型穿越风洞试验段,沿轨道继续前进,滑行进入阻尼滞速阶段,速度快速下降直到停止。测控系统位于风洞两侧列车模型进出入口位置,对列车模型的进出速度进行测量。

图3 列车模型弹射系统Fig.3 Moving train model system
1.3 风压荷载测试
试验采用DTC Initium 网络智能式风洞电子压力扫描阀,测量声屏障表面测点压力以及测试流场的总压与静压,通过下式得到测点的风压系数Cp[12]:
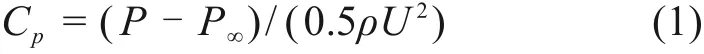
式中:P为封闭式声屏障外壁风压;P∞为来流静压;U为试验风速;ρ为空气密度。
平均风压系数Cpmean与脉动风压系数Cprms[13]定义如下:

式中:Cpmean为平均风压系数;Cprms为脉动风压系数;Cp(t)为t时刻的风压系数;N为测压试验采样点数,试验采样点数为20 000个。
进行横风作业下声屏障外壁风压系数研究时,取来流6,8 以及10 m/s 3 种风速,对应雷诺数为3.7×105,4.9×105和6.1×105。进行列车风作用下声屏障内壁风压系数研究时,取14,17以及23 m/s 3种列车车速,为保证试验结果的稳定性和准确性,每种工况均重复测量3次。
2 横风作用下声屏障外壁的风压分布
2.1 风压系数沿环向的变化规律
图4 为10 m/s横风作用下声屏障的风压系数沿环向的分布规律。由于4个截面的风压系数分布规律相似,仅以中间截面为例分析。 声屏障在迎风侧−23°~20°范围内平均风压系数为正,其值由1.0不断下降至0;由20°开始,风压系数均为负值,20°~63°范围内平均风压系数的数值不断增大,在63°附近出现最大负风压,其值为−3.04;63°~95°范围内圆柱表面的平均风压系数数值持续减小,在95°趋近稳定,其值为−1.0。整体来看,沿顺时针方向,迎风侧的风压迅速由正变负,并在顶部取得极值负风压后风压值先减小后趋于平稳,在背风侧区域风压为负并保持稳定。声屏障的脉动风压系数在−24°~52°范围内保持稳定(约为0.12),在52°~107°范围内脉动风压系数出现最大值0.38,在107°~203°范围内又趋近稳定。此全封闭式声屏障结构平均风压系数分布规律与单圆柱在临界雷诺数区域内的风压系数分布规律[12]相似。
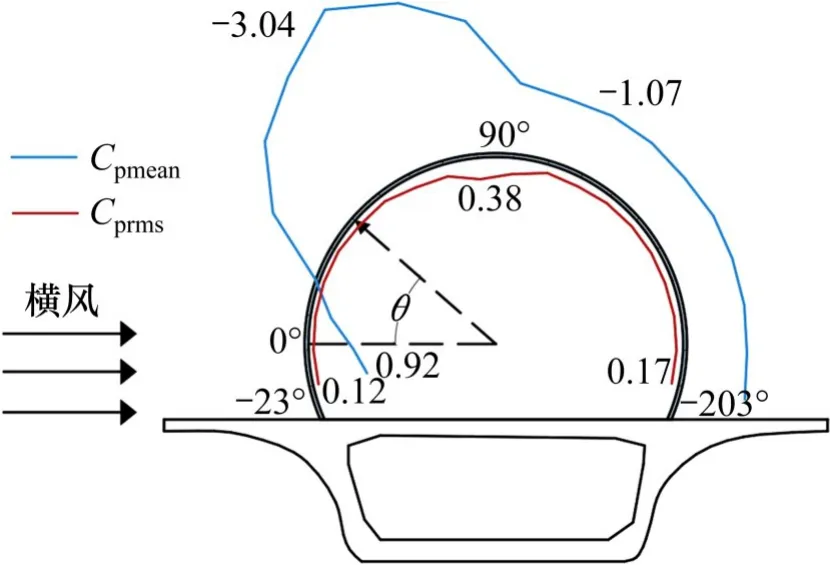
图4 风压系数沿声屏障表面分布图Fig.4 Distribution of wind pressure coefficient on the surface of sound barrier
2.2 雷诺数对声屏障平均风压系数的影响
图5展示了不同雷诺数下声屏障平均风压系数的变化规律。结果显示,在3.7×105~6.1×105的雷诺数范围内,雷诺数对声屏障结构顶部的平均风压系数有影响,对迎风侧和背风侧的平均风压系数影响很小。随着雷诺数的增大,顶部的平均极值风压系数值从−3.38变为−3.04,背风侧的风压稳定点在一定范围内逐步向来流方向推移。
图5 不同风速下的平均风压系数分布Fig.5 Distribution of mean pressure coefficient under different wind speeds
2.3 风荷载体型系数
封闭式声屏障的平均风压系数沿展向差异不大,而环向分布较大,可按等效风压系数考虑结构的风荷载体型系数。在实际工程中,按不同角度划分范围内的风压系数较为繁琐,不利于方便工程师应用,需对封闭式声屏障的风压系数进行简化。根据建筑结构荷载规范(GB50009—2012)[14]和相关文献[7],常用3 种方法简化:利用规范确定外形相似结构的体型系数,区域极值法与平均值法。如图6 所示,3 种方法得到的风荷载体型系数差异明显。规范建议值与声屏障迎风侧分布相近,而顶部与背风侧则相差较大,一方面试验受雷诺数影响,同时没能考虑桥梁对声屏障结构来流的干扰,另一方面声屏障结构形状与规范并不完全一致。平均值法和极值法则根据声屏障结构不同区域的风压分布特点来划分,即迎风侧风压为正,顶部负风压最大,背风侧负风压数值较稳定,其中平均值法采用各区域风压系数的平均值作为体型系数,极值法采用各区域内风压系数的极值作为体型系数。

图6 风荷载体型系数Fig.6 Wind load carrier type coefficients
为了对比以上3种简化方法计算的风荷载系数的准确性,采用MIDAS/civil 软件建立全封闭声屏障主拱肋有限元模型,将等效风荷载施加于模型之上,计算结构静力响应并与采用试验风荷载计算的结果进行对比。依据我国某高速铁路客运专线实际工程,全封闭声屏障拱肋采用H 型钢材,具体尺寸如图7 所示,材料采用Q345 钢材,柱脚边界条件设置为固定支撑。

图7 拱肋截面尺寸Fig.7 Arch rib section size
在10 m/s横风作用下,结构的横向位移分布如图8 所示。在4 种风荷载作用下,声屏障结构位移值均呈“拱顶较大,最大值在拱顶附近,且沿拱顶两侧逐渐减小,柱脚处最小”的分布规律。采用试验风荷和平均值简化风荷载计算的横向位移分布相似,采用规范给定的风荷载计算所得的横向位移的数值偏小,采用极值简化风荷载计算所得的横向位移偏大,远大于采用试验风荷载计算所得的横向位移。

图8 横向位移分布Fig.8 Lateral displacement distribution
表1总结了采用几种等效风荷载计算的全封闭声屏障拱肋拱顶的横向位移和拱脚的内力。结果表明:风荷载采取规范建议取值时,最大位移值、柱脚内力均偏小;采用平均值等效方法取值时,最大位移值和柱脚内力都与采用试验风荷载计算的结果接近;采用极值等效方法取值时,最大横向位移值与一侧柱脚弯矩值明显大于采用试验值计算的结果,其中最大位移和柱脚弯矩是采用试验值计算结果的2 倍,柱脚侧向力为1.3 倍。从经济、安全以及工程实际角度综合考虑,建议采用平均值乘以放大系数作为声屏障结构的风荷载体型系数。综合考虑最大位移值与柱脚内力与采用试验风荷载计算一致的要求,建议放大系数取值1.3,从而全封闭式圆截面声屏障的风荷载体形系数建议取值为:迎风侧0.8,顶部−2.5,背风侧−1.4。
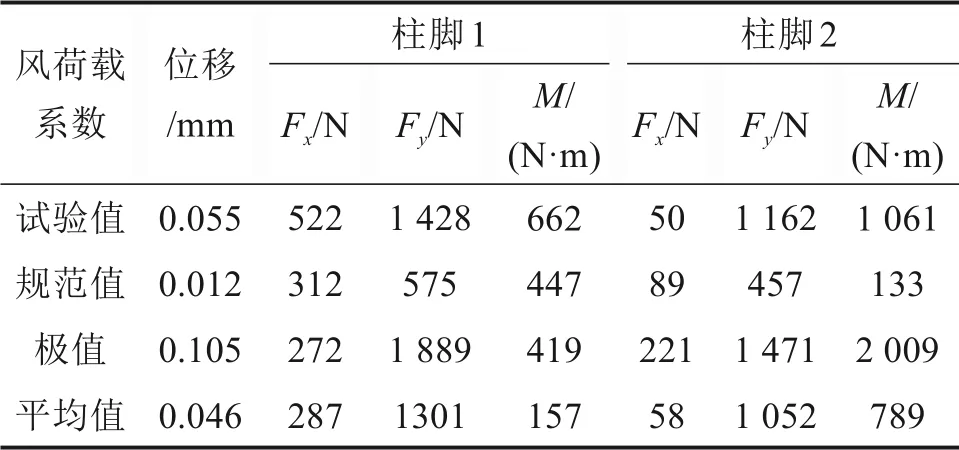
表1 拱顶横向位移和柱脚内力对照表Table 1 Comparison table of lateral displacement of vault and internal force of column foot
3 列车风作用下声屏障内壁风压分布
图9为列车风作用下封闭式声屏障内壁的脉动风压时程曲线。列车通过时的脉动风压波峰、波谷,即正压峰值、负压峰值,且列车模型与声屏障同比例缩尺,其列车试验速度与实际车速相等。

图9 脉动压力时程曲线(1/4处截面)Fig.9 Pulsating pressure time history of the inner wall of the sound barrier
3.1 单车通过声屏障的风压荷载
图10为不同车速下声屏障(中间截面)的压力峰值分布,正峰值和负峰值均随列车运行速度的增加而增大,近轨侧的压力峰值明显高于顶部和另一侧。车速较低时,列车运行引起的压力波较小,测点间的压力差不明显。在23 m/s车速时,近侧的压力峰值均明显高于远侧,最大相差达16%。可见同一截面上的压力峰值存在着明显差异,可能对结构受力不利。随着列车车速的提高,环向风压差异更加明显,这种现象与高速列车通过隧道横截面上压力分布结论一致[15]。
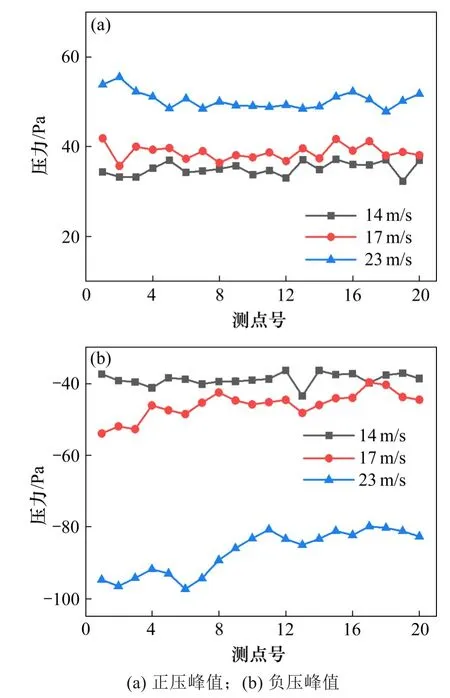
图10 不同车速下声屏障的压力峰值Fig.10 Extreme wind pressure of sound barrier under different train speeds
图11 为3 种运行速度下声屏障中间截面的压力最大幅值。结果显示,声屏障压力幅值与列车运行速度的平方近似成正比关系。这与文献[15−16]隧道空气动力学的研究结论相近,其中文献[16]拟合的列车穿过隧道时车速与隧道壁面压力幅值关系为y=0.013x2.15。

图11 声屏障压力幅值同车速关系Fig.11 Relationship between sound barrier pressure amplitude and train speed
图12 为单列车以17 m/s 车速通过声屏障的压力峰值图。沿声屏障长度方向,不同截面的压力变化情况不完全相同。出入口截面受洞口效应影响,列车经过引起的气流会变形迅速传递至声屏障外。从图中可知,列车驶入声屏障时,正压峰值有一个从小变大再减小的过程,1/4 处截面的压力峰值(58 Pa)较大,入口截面(52 Pa)次之,出口截面(约为22 Pa)最小,中间截面正压峰值约等于1/4处截面和出口截面的平均值(40 Pa),整体来看声屏障内壁的正压峰值沿环向变化不大。负压峰值在行车一侧(测点1~6)达到−54 Pa,顶部(测点7~14)达到−44 Pa,远侧(测点15~20)仅−37 Pa,可看出负压峰值沿环向差异明显,均服从近侧较大、远侧较小的规律。

图12 压力峰值分布Fig.12 Pressure peak distribution
3.2 会车时声屏障的风压荷载
图13 为列车以17 m/s 车速会车时声屏障的压力峰值分布,试验中下游列车的车速稍高于上游车速,导致该侧压力增幅稍大。会车时,各截面测点的压力峰值较单车时加强明显,交会处测点的极值负压(−89 Pa)大于1/4 处截面(−73 Pa),两者压力峰值分布相似,沿测点变化正压峰值变化较小,负压峰值变化稍大。出入口截面的压力峰值沿测点变化较大,两侧的压力峰值有明显的加强。可知,当列车在声屏障内交会时,交会区域的压力峰值明显较高,顶部位置的压力极值(79 Pa)近似为单车时(40 Pa)的2 倍;在非交会区域,列车近侧的测点压力峰值较大,远侧测点的压力峰值较小。

图13 会车工况压力峰值分布Fig.13 Peak pressure distribution under driving conditions
4 结论
1) 声屏障外壁的平均风压系数和脉动风压系数分布规律与单圆柱的风压分布相似;雷诺数对声屏障结构顶部的平均风压系数影响稍大,对迎风侧和背风侧的平均风压系数影响较小;根据横向最大位移和柱脚内力等效的原则,建议声屏障风荷载体型系数取值为:迎风侧0.8,顶部−2.5,背风侧−1.4。
2) 列车通过声屏障时,沿声屏障长度方向,不同截面的压力变化情况不完全相同;声屏障内壁的负压峰值沿环向差异明显,服从近侧较大,远侧较小的规律,且压力幅值与列车速度的平方近似成正比关系。
3)2 车交会时,交会区域的极值风压明显高于单车通过,最大极值风压出现在交会截面;交会区域极值风压高于非交会区域,最高极值风压约为单车通过时极值风压的2倍。

