400 km/h速度下编组长度对高速列车隧道交会压力波的影响

钟沙，钱博森，杨明智，尹小放，苏伟华

(中南大学 交通运输工程学院，轨道交通安全教育部重点实验室，湖南 长沙410075)

近年来，中国高铁不断发展，截至2019年底，不仅在运行速度上以350 km/h 领先于世界各国，并且在规模上也以3.5 万公里的营业里程与3 500标准列的动车组保有量稳居世界第一[1]。然而，随着社会的发展，人们对出行速度的需求越来越高。因此，400 km/h速度等级的高速铁路研发建设亟待开展。随着动车组行驶速度的增加，相关的空气动力学问题也愈加突出[2−3]。列车进入隧道时，隧道与列车对空气的挤压作用引发的压力波会导致隧道内交变压力的产生，一方面会严重影响乘客舒适性，另一方面也对隧道内衬砌与车体结构的强度提出了一定的挑战[4−5]。当列车隧道交会时，该问题会更加严重[6−7]。此外，随着列车编组长度的增加，隧道壁面与列车表面交变压力幅值也会受到严重的影响。因此有必要对400 km/h 速度等级下，编组长度对动车组隧道交会压力波的影响进行研究。国内外学者开展了针对时速400 km 高速列车的空气动力学研究。魏雨生等[8]通过数值模拟方法，发现单车由300 km/h 提速到400 km/h 过70 m2标准隧道时，列车表面和隧道壁面最大压力峰峰值分别提高了90.4%和65.3%。邱利伟等[9]基于数值仿真，对400 km/h 的7 种型号的8 车编组动车组列车设计方案进行了气动性能分析，提出了高速动车组气动性能评估模型。胡啸等10]采用重叠网格技术，研究了速度和线间距对隧道交会列车车体两侧压差波动特性的影响，研究结果表明，400 km/h 下压差最值平均比350 km/h 大26% 。对于不同编组长度列车的气动性能，国内外学者也积极开展了许多研究。黄志祥等[11]采用风洞试验，研究了编组长度对各节车气动阻力分布规律的影响，提出了长编组列车与3车编组列车气动阻力系数之间的估算关系式[11]。MARTIEZ 等[12]通过实车试验发现单车过隧道时，初始压缩波峰值随列车编组长度的增加而增大。周丹等[13]通过数值模拟方法，分析了时速350 km 不同编组长度列车的表面交变压力载荷，发现单车过隧道时，车体表面压力峰峰值由3 车编组到8 车编组增大14.0%，列车隧道交会时该值增大26.4%。上述对于时速400 km高速列车空气动力学的研究，较少涉及到编组长度和隧道交会对列车气动性能的影响。而在不同编组长度列车的气动性能研究中，主要分析对象是350 km/h 或以下速度等级的动车组。因此，本文从时速400 km 高速列车隧道交会出发，通过分析压缩波与膨胀波的叠加，研究编组长度对列车表面与隧道壁面瞬变压力的影响。

1 数值计算模型

1.1 列车及隧道模型

列车编组形式采用头车+中间车+尾车，3 车、8 车和16 车编组列车如图1 所示。列车模型包含风挡及转向架等精细模型，以确保结果的精确性。如图2 所示，特征长度H表示列车高度(3.85 m)，头尾车长度均为7.05H，中间车长度为7.19H。由于2 动车组在隧道中等速交会，并且同时进入隧道，因此2列车表面压力随时间变化规律一致。图2(c)展示了头车、中间车和尾车表面的测点布置图，分别布置有10 个、6 个、10 个测点，图中括号内编号相邻的测点位于非相交侧的表面上。因此3 车，8 车和16 车编组分别布置有26 个，56 个和104个测点。

图1 编组形式Fig.1 Train formation

图2 列车模型尺寸及测点布置示意图Fig.2 Size of train model and layout of measuring points

隧道模型采用100 m2双线标准隧道，断面示意图如图3(a)所示，线间距为5 m。由于列车隧道交会时存在一个最不利隧道长度使得列车表面压力波动幅值最大，因此本文选择最不利长度隧道进行隧道气动效应的研究，该长度可由公式(1)[14]计算得出。

图3 隧道断面及壁面测点布置示意图Fig.3 Tunnel section shape and layout of measuring point

其中，Ltr,Ma分别为动车组长度及运行马赫数。因此不同编组长度列车隧道交会的最不利隧道长度如表1所示。

表1 隧道交会最不利隧道长度Table 1 Most unfavorite tunnel length

为了记录隧道壁面的交变压力，如图3(b)所示，在不同长度的隧道壁面上均布置了16个测点，其中5 号和6 号测点位置处于距隧道洞口一倍车长处，7，8，9和10号测点位于隧道中间位置。

1.2 计算域及边界条件

在本研究中，采用滑移网格法模拟列车与列车、列车与隧道之间的相对运动。如图4 所示，2动车组均距离隧道洞口50 m，滑动区域A 和区域B 分别包含列车A和列车B以400 km/h的速度向相反方向移动。在固定区域C中，隧道表面和地面均设置为无滑移壁面，其余均设置为压力出口。滑动区域与固定区域的接触面设置为交界面。

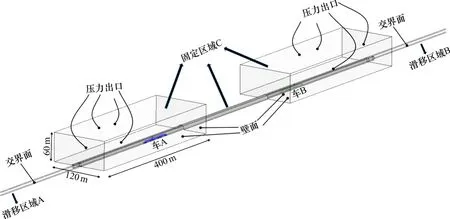
图4 计算域和边界条件Fig.4 Computational domain and boundary conditions

1.3 计算网格

由于动车组模型包含转向架等复杂结构，因此选择混合网格再对计算域进行离散。如图5 所示，列车周围的区域采用四面体网格进行离散，其余区域均被离散为六面体网格。3 车、8 车和16车编组隧道交会时网格数量分别为1 864万，3 574万和6 435万。

图5 网格分布Fig.5 Mesh distribution

1.4 数值计算方法

本文选用基于有限体积法的商用求解器AN‐SYS Fluent。采用非定常、黏性和可压缩的N-S 方程求解列车隧道交会时的流场。相对于广泛应用于列车隧道交会流动数值模拟的k-ε湍流模型，RNG 模型在函数模型中增加了一项，提高了流场分析的准确性和可信度[15]，因此，本文采用RNGk-ε湍流模型。此外，采用SIMPLE 算法求解速度和压力的耦合方程。选择二阶迎风格式求解对流项和扩散项。时间步长设置为0.000 1 s，内迭代步数为50步。

1.5 数值验证

通过中南大学轨道交通安全教育部重点实验室的动模型试验平台进行400 km/h 高速动车组隧道交会试验。如图6 所示，选择缩比为1:20 的3 车编组列车与隧道模型，压力测点的相对位置与2.2中所述的一致。

图6 动模型实验Fig.6 Moving model test

图7(a)和7(b)分别展示了3 车编组动车组以400 km/h于最不利长度隧道中心交会工况下，车体表面H3 号测点与隧道壁面8 号测点的压力时程曲线，曲线的起点和终点分别对应车头进入隧道和尾车离开隧道的时刻。由于数值模拟的隧道长度是动模型试验长度的20 倍，因此将试验的时间进行相应的转换。同时由于雷诺数大于3.6×105，模型尺寸对列车周围的流场影响很小，因此试验测点的压力值可以代表全尺寸模型的压力值[16]。如图7 所示，除了隧道壁面8 号测点2.8 s 附近的波峰值差距较大外，其余时间的数值计算曲线与动模型曲线吻合得都比较好。图中Pmax与Pmin分别代表正、负幅值，ΔP表示压力峰峰值，即正负压幅值之差。数值计算结果与动模型试验结果的最大压力峰峰值相差不超过3.6%，证明了数值计算结果的准确性。

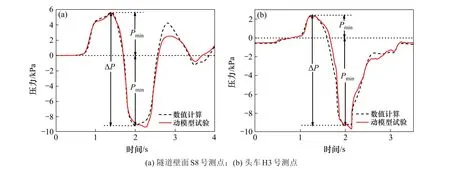
图7 数值模拟与动模型试验测点压力时程曲线对比结果Fig.7 Comparison results of pressure time history curve of measuring point between numerical simulation and moving model test

2 结果及分析

2.1 动车组表面压力分析

为了分析隧道压力波对动车组表面压力载荷的影响，图8 展示了交会侧车体表面压力峰峰值ΔP沿车长方向分布曲线。横坐标表示距离头车鼻尖点的水平距离，纵坐标表示压力变化幅度ΔP。从图8可知，车体表面压力峰峰值由头至尾呈逐渐减小的趋势。此外，随着编组长度由3车增加到16车，最大压力峰峰值由12.05 kPa增加到15.18 kPa，涨幅为25.98%，而最小压力峰峰值只由9.52 kPa增加至9.81 kPa，涨幅为3.00%。

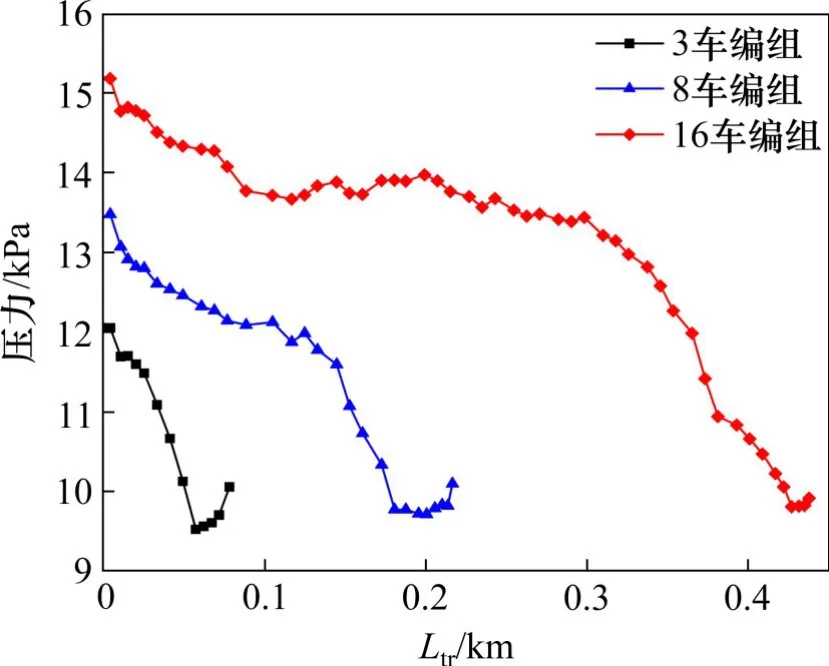
图8 沿车长方向车体表面压力峰峰值分布曲线Fig.8 Distribution of ΔP along the train

图9(a)和9(b)分别给出了头车H1 号测点和尾车的T1号测点。从图9可知，编组长度由3车增加到16 车，头车测点的正压幅值急剧增加，由4.19 kPa 增加至7.06 kPa，负压幅值小幅下降，由−7.86 kPa 减小至−8.12 kPa；尾车测点的正压幅值由2.09 kPa 下降至0.36 kPa，负压幅值由−7.95 kPa 下降至−9.55 kPa。由此可知，动车组隧道交会时，编组长度的增加导致头车表面的正压幅值上升，是车体表面最大压力幅值随之增大的主要原因。

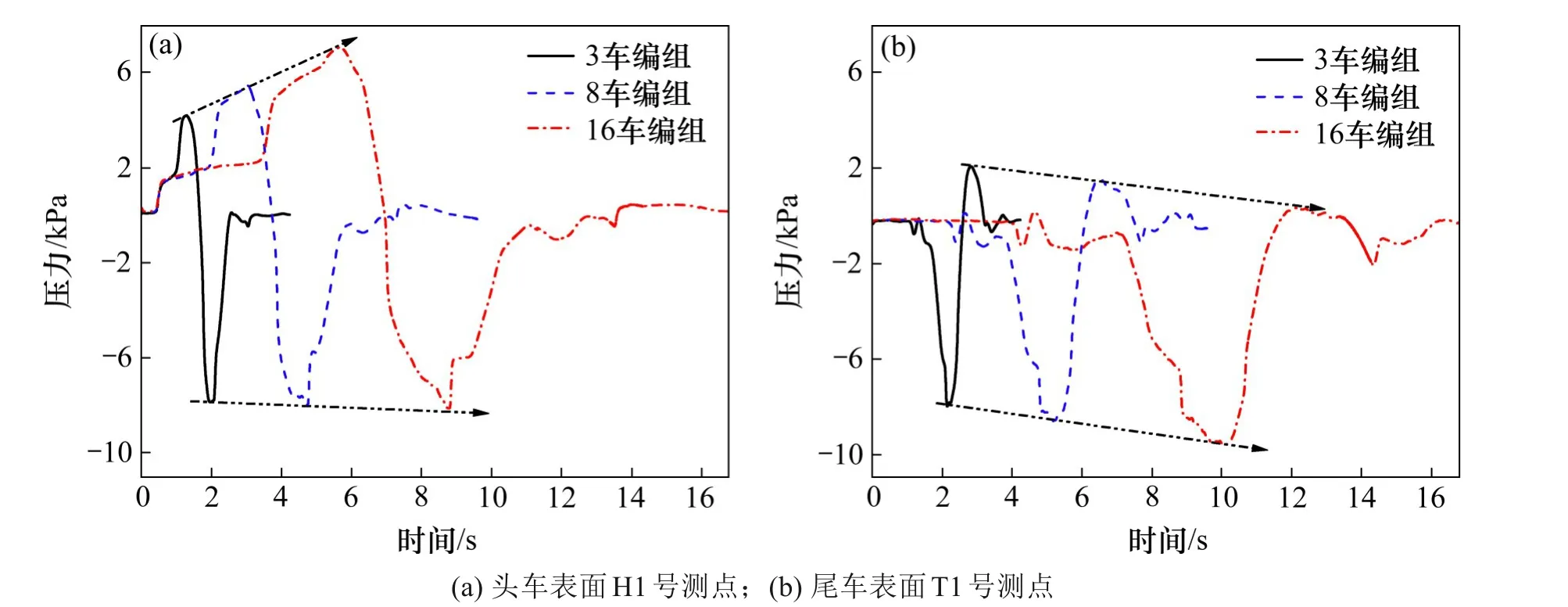
图9 动车组表面典型测点压力时程变化曲线Fig.9 Pressure time history curve of typical measuring points on train surface

2.2 隧道壁面压力分析

图10展示了3车，8车和16车编组动车组于最不利长度隧道交会时，隧道壁面各测点压力峰峰值，横坐标表示测点编号(测点布置如图6 所示)，纵坐标表示压力峰峰值。从图6可知，位于同一隧道截面的测点压力峰峰值相差均不超过6.7%，因此400 km/h 速度下动车组隧道交会时，隧道三维效应并不明显。此外，隧道壁面最大压力峰峰值出现在隧道中部截面上，即7，8，9 和10 号测点，编组长度由3 车增加到16 车，最大压力峰峰值由14.73 kPa增加至19.19 kPa。

图10 隧道壁面各测点压力峰峰值分布曲线(测点位置如图3所示)Fig.10 Distribution of ΔP on tunnel wall

2.3 交变压力时程分析

为了分析动车组隧道交会时，编组长度对列车表面与隧道壁面压力变化影响的原因。图11(a)和11(c)分别给出了8 车编组与16 车编组通过最不利长度隧道时，压力波的传播情况，图中HA和TA分别代表动车组A 的头车与尾车鼻尖点，HB和TB分别代表动车组B 的头车与尾车鼻尖点，CAi和CBi分别代表动车组A 和B 通过隧道产生的压缩波，EAi和EBi分别代表动车组A 和B 通过隧道产生的膨胀波。同时图11(b)给出了隧道壁面8 号测点压力时程曲线。

图11 100平标准隧道壁面8号测点压力时程变化分析Fig.11 Time histories of pressure variation in a 100 m2 standard tunnel

从图11 中可知，压缩波与膨胀波会导致测点压力上升与下降，头车与尾车经过测点时分别会导致测点压力下降与上升。此外，2 相向行驶的动车组头车进入隧道时，引起的初始压缩波叠加导致该测点压力急剧上升，形成正压幅值Pmax。初始压缩波在隧道洞口反射回的膨胀波、尾车进入隧道时引起的初始膨胀波以及头车的经过导致该测点压力急剧下降，形成负压幅值Pmin。值得注意的是，16车编组通过最不利隧道长度时，相对于8车编组工况，由于初始压缩波与初始膨胀波的强度更大，并且压缩波与膨胀波之间的时间间隔更长，由此导致正压幅值增大，负压幅值减小，从而使得压力峰峰值急剧增大。

3 结论

1) 车体表面压力峰峰值由头至尾呈逐渐减小的趋势。随着编组长度由3 车增加到16 车，最大压力峰峰值由12.05 kPa 增加到15.18 kPa，涨幅为25.98%，而最小压力峰峰值只由9.52 kPa 增加至9.81 kPa，涨幅为3.00%。

2) 位于同一隧道截面的测点压力峰峰值相差均不超过6.7%，因此400 km/h 速度下动车组隧道交会时，隧道三维效应并不明显。

3) 编组长度由3 车增加到16 车，隧道壁面最大压力峰峰值由14.73 kPa增加至19.19 kPa。