模拟研究和设计高强度低生热聚合物复合材料

王小勇，赵婷钰,左玉鑫，陈 鹏，钱家盛

(安徽大学 化学化工学院,安徽 合肥 230601)

聚合物复合材料具有优良的加工性能和机械性能，广泛应用于众多领域.例如，橡胶是一种典型的聚合物复合材料，在轮胎、减震、密封、绝缘等领域具有不可替代的地位.橡胶材料的配方和制备工艺较复杂，但其主要成分是柔性的高分子链和炭黑等.研究表明，炭黑或二氧化硅等无机填料的引入，能够显著提高橡胶的拉伸强度、抗疲劳性等.但在实际应用中，填料在聚合物基体中难以均匀分散，容易形成三维填料网络.在交变应力作用下，橡胶部件发生高频往复形变，填料颗粒之间相互摩擦、网络结构的解体和恢复以及聚合物链端的剧烈运动都会导致体系发生严重的动态滞后生热现象.随着热量的聚集和持续作用，加快聚合物老化、橡胶部件的功能失效、使用寿命减少.

为了减少橡胶材料的动态生热，人们探索了多种体系配方和加工工艺.其中，Qin等将聚苯乙烯-丁二烯共聚物与高度对称的异氰酸酯和多元醇交联，通过大分子自组装形成均匀的网络，结果表明这种新型弹性体巧妙地平衡了滚动阻力、耐磨性和抗湿滑性，解决了困扰轮胎行业多年的“魔三角”问题.Mayura等从生物废料中提取具有高度分散性的二氧化硅，代替炭黑加入橡胶轮胎中，结果发现轮胎的滚动阻力显著降低.

上述研究结果说明，通过材料设计和复合体系微观结构的调控，可以实现橡胶材料兼顾高强度和低滞后生热性能.然而，橡胶体系的配方组成和实验加工工艺都非常复杂，难以从宏观角度阐述机理，计算机模拟研究方法可以从微观角度出发，对橡胶体系进行结构设计和性能调整.例如，北京化工大学刘军课题组通过粗粒度分子动力学模拟方法，将双端功能化的聚合物链通过化学吸附连接到纳米颗粒表面，从而构建一种新型聚合物填料网络，这种新型聚合物填料网络在表现出优异力学强度的同时保持低滞后生热性能，其模拟结果与实验一致.由此可以看出，计算机模拟能够对材料的性能进行预测、对实验过程进行优化、对实验的结果进行理论解释，进而为实验提供理论指导.

为了研究和设计具有优异力学强度和生热性能的橡胶复合体系，采用分子动力学方法研究聚合物基复合材料中填料分布、聚合物链性质以及体系微观结构对力学强度和动态滞后生热性能的影响，并结合研究结果，设计出一款同时具备高力学强度和低滞后生热的高性能橡胶复合材料.

1 模拟方法与模型

笔者采用粗粒度分子动力学方法模拟高分子复合体系，模拟过程采用无量纲单位.模型中每条聚合物链含有200个粗粒化模拟单元，共75条聚合物链，每个粗粒化单元的质量为

m

，直径为

D

，填料的直径为4

D

.对于聚合物与聚合物、聚合物与填料以及填料与填料之间的非键相互作用势,采用Lennard-Jones(LJ)势能来描述，如式(1)所示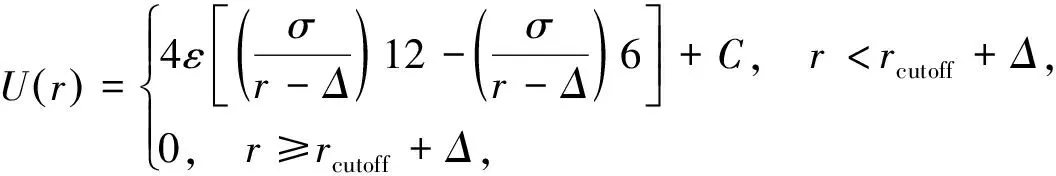

(1)

其中：

ε

是相互作用能参数，

r

为两原子间距离，

σ

为平衡距离.在粗粒化模型中，使用珠子表示粗粒化结构单元，然而不同结构单元具有不同的直径，因此引入

Δ

来消除两粒子直径不同而引起的体积效应.对于聚合物与聚合物之间相互作用能，

Δ

为0，对于聚合物与填料以及填料与填料之间的相互作用能，

Δ

分别为

R

-

σ/

2和2

R

-

σ

，

R

为填料半径，NP为填料.各组分粒子间相互作用势能参数见表1.对于聚合物链上成键原子间的键势能，采用可扩展非线性弹性(FENE)势能函数，如式(2)所示

表1 复合体系中各组分间相互作用能变量与参数

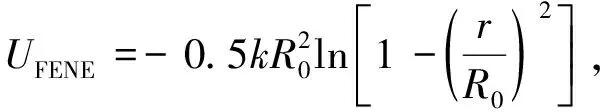
(2)

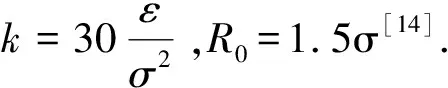
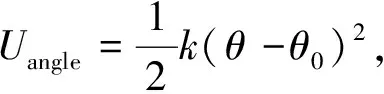
(3)

其中:

θ

为平衡角度，

k

代表弯曲角势能系数，用来调控体系的刚柔性.在整个研究过程中，对研究体系

X

，

Y

，

Z

3个维度设置周期性边界条件.首先，采用等温等压系综对初始模型进行松弛，体系压力

P

=1.0，温度

T

=1.0，高于其玻璃化转变温度(

T

≈0.48).接着使用正则系综对体系进一步弛豫.当体系达到充分弛豫(体系的温度、能量等趋于稳定)之后，计算体系的应力-应变曲线以及动态滞后生热.应变根据式(4)计算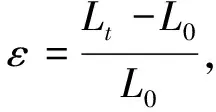

(4)

其中：

L

表示体系

t

时刻拉伸后长度，

L

表示体系原长.

X

方向的应力采用式(5)计算

(5)

其中：泊松比

μ

=0.5，

P

=∑

P

/

3为静水压力.对

X

，

Y

，

Z

3个方向进行独立拉伸，对结果取平均，以此得到更精准的应力-应变曲线.

橡胶在拉伸和压缩过程中的应力-应变曲线会产生滞后圈，对滞后圈进行面积积分所求得的值，即为滞后损耗，具体计算方法见文献[21].整个模拟过程采用桑迪亚(Sandia)国家实验室开发的大规模原子/分子并行模拟器(large-scale atomic molecular massively parallel simulator, 简称LAMMPS)进行.

2 结果与讨论

2.1 填料分布对力学强度和滞后生热性能的影响

为研究填料分布对力学强度和滞后生热性能的影响，在聚合物中构建了4种不同分散状态的填料模型，如图1(a)所示，其中f-disperse表示填料均匀分散在聚合物中；h-disperse表示少量填料形成聚集，大部分填料均匀分散在聚合物中；h-aggregate表示大部分填料形成聚集，少量填料均匀分散在聚合物中；f-aggregate表示填料在聚合物中完全聚集.图中红色球表示填料，蓝色球表示聚合物，填料直径为4

D

，填充含量为11.71%.填充含量的计算方法为填料体积与模拟盒子体积的比值.当体系达到充分弛豫之后，观察填料分布情况，结果如图1(b)表示.为了进一步表征填料分布状态的差异，测定不同分布状态的径向分布函数(radial distribution function,简称RDF)，其结果如图1(c)所示.结合图1(b)和图1(c)可以看出，f-disperse，h-disperse，h-aggregate以及f-aggregate模型中填料粒子的团聚程度逐渐增大.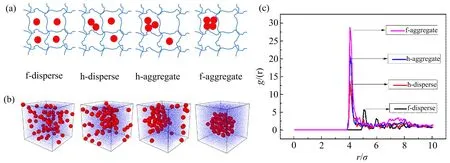

图1 模式示意图(a)、填料分布(b)与填料径向分布函数(c)

为探究填料分布对体系性能的影响，计算填料不同分布状态下的应力-应变曲线和滞后圈面积，结果如图2所示.其中，图2(a)表示应力-应变曲线，图2(b)表示滞后圈面积.

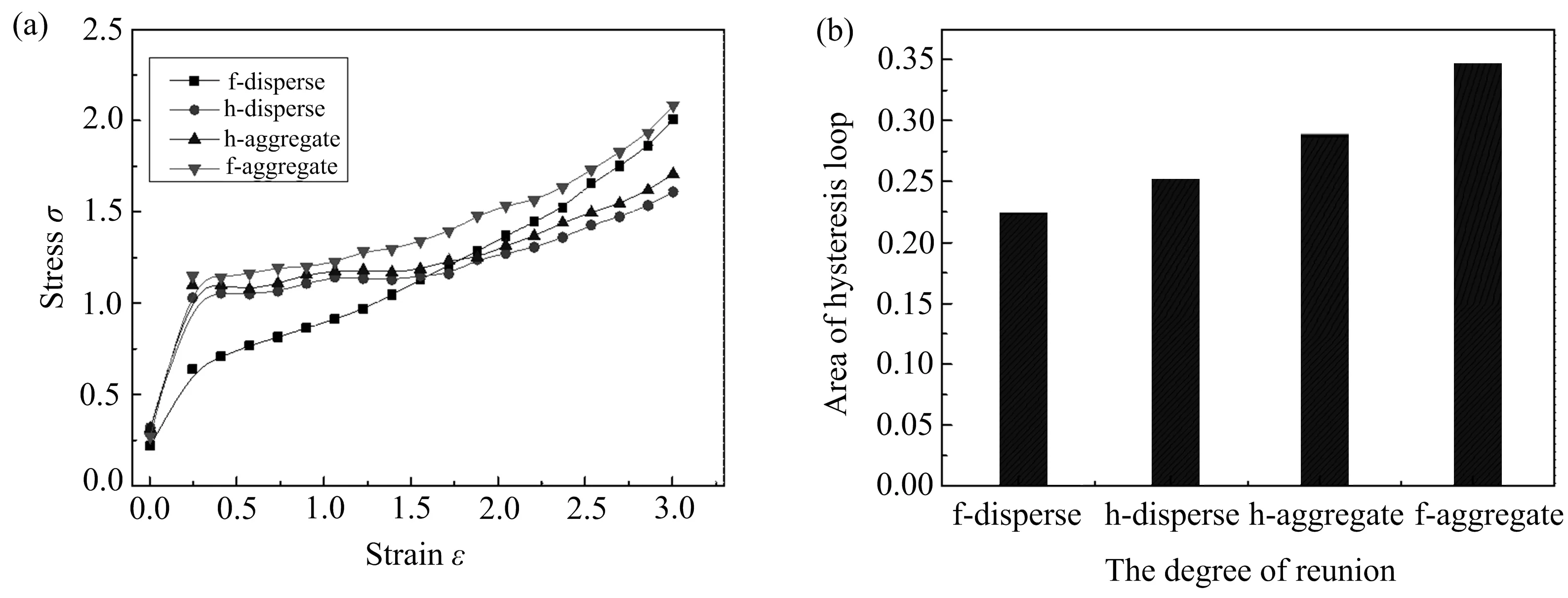
图2 应力-应变曲线(a)及滞后圈面积(b)

由图2(a)可以发现，在较小应变下(

ε

<1.5)，由于填料网络的作用，应力随着填料团聚程度的增加而逐渐增大；当体系拉伸到一定程度后，填料网络解体，完全分散体系力学强度迅速增大，最终与完全团聚体系力学强度相同.由图2(b)可以发现，体系动态滞后生热性能随着填料团聚程度的增大而增大，这是由于随着团聚程度的增大，填料间相互接触更加频繁，导致体系的生热性能随之增大.

2.2 聚合物链末端数目对力学强度和滞后生热性能的影响

聚合物复合材料的能量损失主要来自填料-填料、填料-聚合物链以及聚合物链-聚合物链间的动态接触.其中，聚合物链末端比其他链节具有更大的自由度，可能会引起热量的累积.因此，设计5种链节数目相同，链端数目不同的体系，如图3(a)所示.图中模型依次为：环型(loop)，每条链含有0个末端；线型(linear)，每条链含有2个末端；四臂星型(4-arm)，每条链含有4个末端；六臂星型(6-arm), 每条链含有6个末端；十二臂星型(12-arm)，每条链含有12个末端.当体系充分平衡之后，计算应力-应变曲线和滞后圈面积，结果如图3(b)～(c)所示.

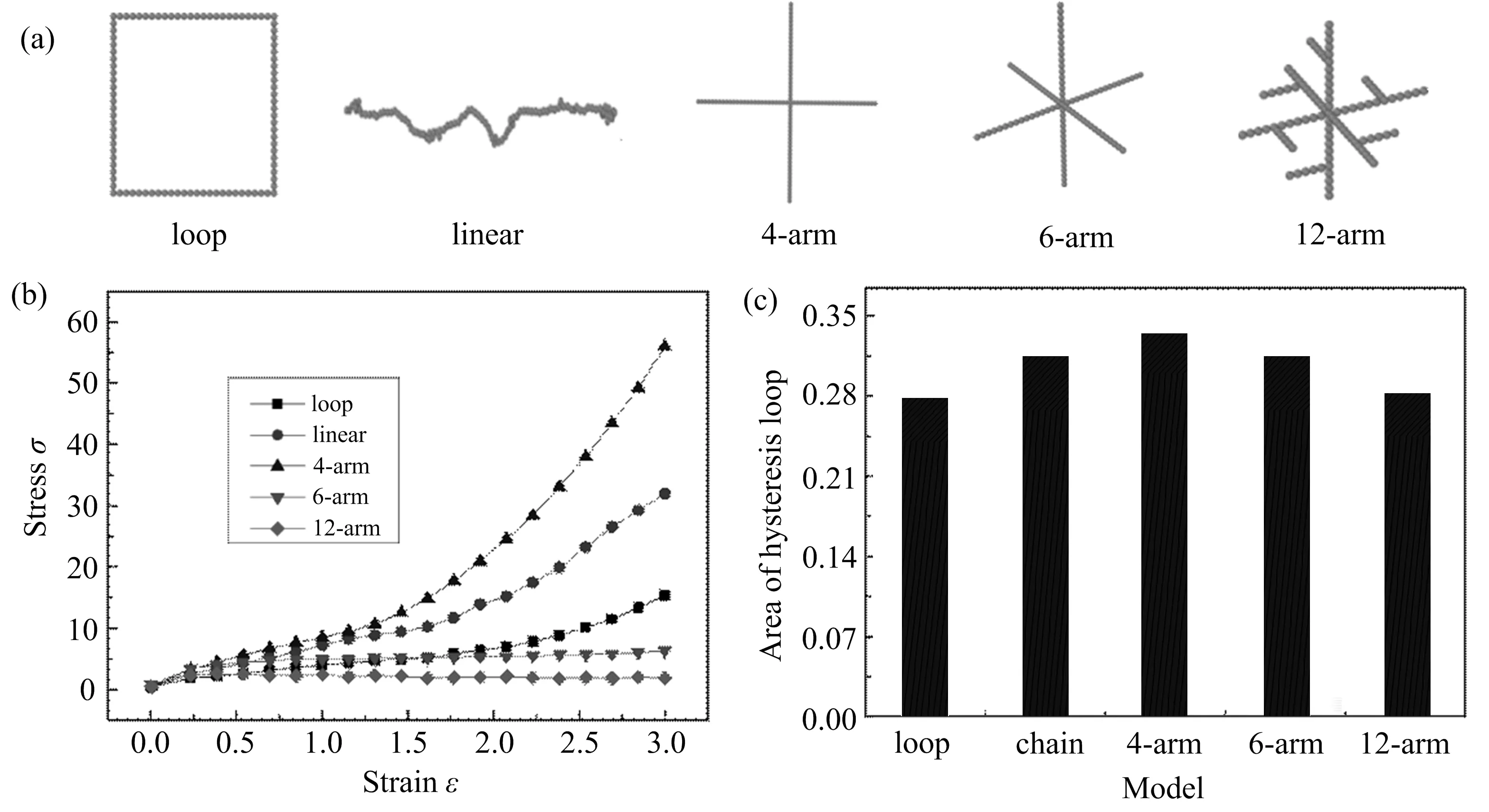
图3 不同链结构模型示意图(a)、应力-应变曲线(b)及滞后圈面积(c)

由图3发现，随着链端数目(臂数)的增加，体系力学强度和滞后生热性能逐渐增大，当链端数目增加到一定程度之后，力学强度和滞后生热性能开始降低.这是由于在链节数相同的情况下，对于高度支化体系，支化臂长减小，缠结程度和运动阻力变小，力学强度和滞后生热性能随之降低.

2.3 聚合物链段刚性对力学强度和滞后生热性能的影响

通过改变公式(3)中的弯曲角势能参数

k

来调控聚合物链的刚柔性，当

k

=0时，表示柔性聚合物链.依次设置

k

=0,10,30,50,70来逐渐增加聚合物链的刚性，研究聚合物链段刚性对力学强度及滞后生热性能的影响，如图4所示.其中图4(a)为体系的应力-应变曲线，图4(b)为滞后圈面积.研究结果表明，随着聚合物链刚性的增强，力学强度和滞后生热性能都随之升高.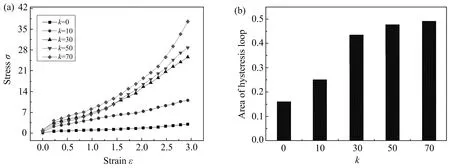

图4 应力-应变曲线(a)及滞后圈面积(b)

为研究交联聚合物体系的力学强度和滞后生热性能，设计了3种交联体系，如图5(a)所示，图5(a)上方为模型示意图，下方为平衡后模型图，其中蓝色表示柔性链，红色表示刚性链.soft表示柔性(

k

=0)聚合物之间交联；soft-rigid表示柔性(

k

=0)聚合物与刚性(

k

=70)聚合物交联，形成刚-柔嵌段共聚物；rigid表示刚性(

k

=70)聚合物间交联.测试其力学强度及滞后生热性能，结果如图5(b)～(c)所示.其中图5(b)为应力-应变曲线，图5(c)为滞后圈面积.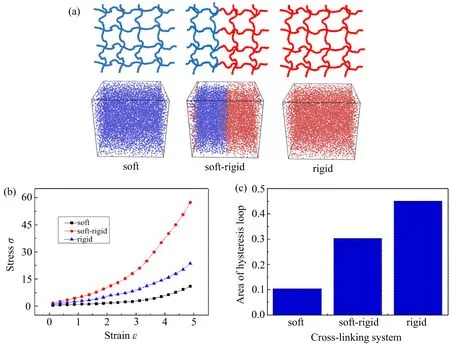

图5 刚-柔嵌段共聚物模型示意图和体系平衡后模型图(a)、应力-应变曲线(b)及滞后圈面积(c)

由图5所示的计算结果发现，刚-柔嵌段共聚物呈现出优异的力学强度，在拉伸3倍应变下，刚-柔嵌段共聚物的力学性能相较于柔性和刚性聚合物分别提升570%和230%，生热性能介于柔性交联和刚性交联之间.这是因为在刚-柔嵌段共聚物中刚性链与柔性链之间排列更加紧凑，导致刚-柔嵌段共聚物的链取向高于柔性聚合物和刚性聚合物，因此，刚-柔嵌段共聚物具有更加优异的力学强度，该结果与北京化工大学Wan等发现的刚柔共混体系具备更优异力学强度的结论是一致的.另外，笔者还测试了

k

=0的柔性链与

k

=30的刚性链形成刚-柔嵌段共聚物，发现同样具备优异的力学强度.

2.4 高力学强度低滞后生热模型的设计

结合以上研究结果可以发现，通过均匀分散填料和减少聚合物的末端数量可以降低聚合物体系在动态形变过程中的生热现象，且刚柔嵌段共聚物具有更优异的动态力学强度.因此，笔者设计了一款以纳米颗粒为交联点，将聚合物链两端通过化学键连接到纳米颗粒上形成环状，相邻的环互穿形成物理交联网络，如图6(a)所示，红色球表示填料颗粒，蓝色球表示柔性聚合物，绿色球表示刚性聚合物.其中nP为传统物理混合模型，clasp为设计的新型聚合物复合材料；依据2.3的研究结果，在clasp模型的基础上，将一半柔性聚合物改为刚性(

k

=70)，形成block模型.将3种模型充分平衡之后，观察填料分布图并测试3种模型的径向分布函数，结果如图6(b)～(c)所示.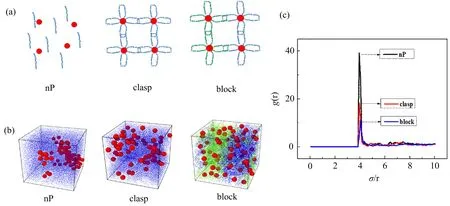

图6 模型示意图(a)、填料分布图(b)及填料径向分布函数(c)

由图6所示的研究结果可以发现：clasp模型与block模型都能够有效地提高填料的分散性，这是因为填料表面接枝聚合物，增加了填料与聚合物之间的相容性，同时限制填料的运动.计算3种模型的应力-应变曲线和滞后圈面积，计算结果如图7所示.其中图7(a)为应力-应变曲线，图7(b)为滞后圈面积；nP-rigid表示物理混合模型，聚合物链为刚性(

k

=70)；nP-soft表示物理混合模型，聚合物链为柔性(

k

=0)；clasp-rigid表示环扣模型，聚合物链为刚性(

k

=70)，clasp-soft表示环扣模型，聚合物链为柔性(

k

=0).研究结果表明：与传统物理混合模型nP相比，clasp模型在柔性(

k

=0)和刚性(

k

=70)状态下，力学性能分别提升230%和310%，生热性能分别降低20%和40%.block模型在clasp模型的基础上，进一步提高了力学强度，与柔性和刚性状态下clasp模型相比分别提升了640%和150%，并且生热性能介于柔性与刚性clasp模型之间.这是由于将聚合物链末端接枝到填料颗粒表面，增加了填料与聚合物的相容性，同时限制填料运动，使填料分散更均匀，减少填料间的相互接触，进而降低体系的生热性能.而聚合物环互穿，增加了聚合物的缠结程度，使得体系呈现出更加优异的力学强度.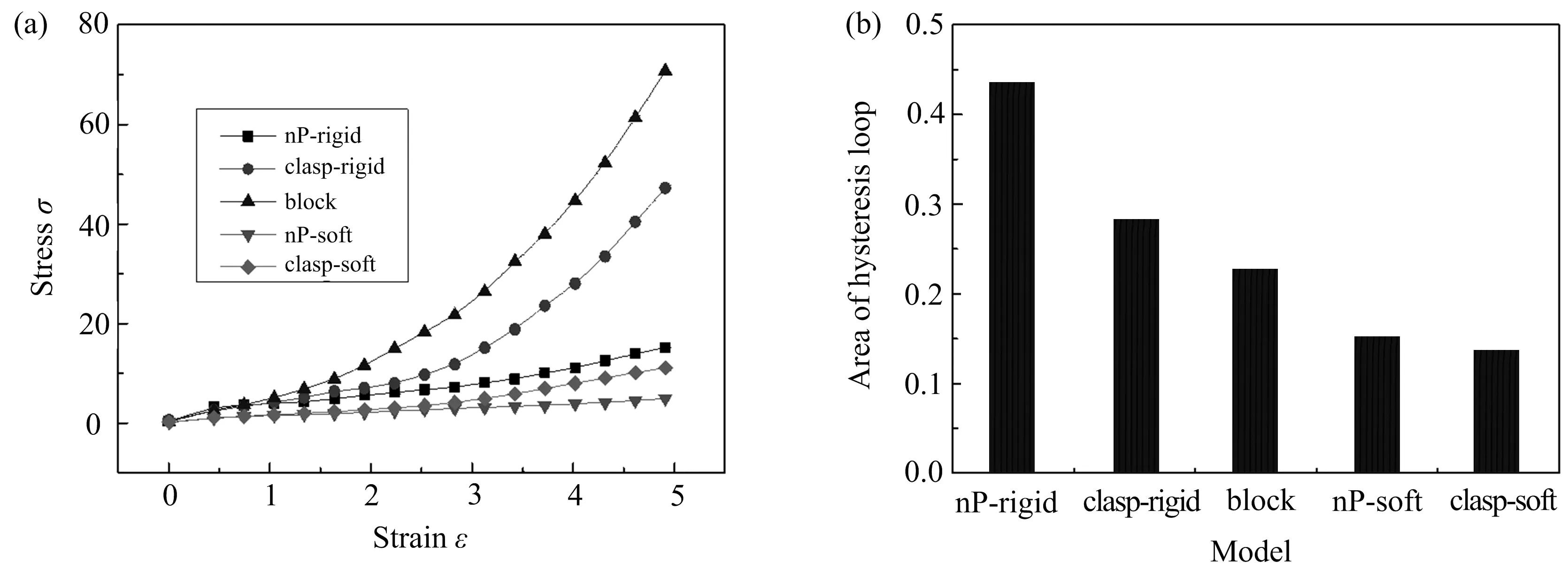

图7 应力-应变曲线(a)及滞后圈面积(b)

3 结束语

通过分子动力学方法构建橡胶的填充交联高分子模型，笔者系统研究了模型参数对体系力学强度以及动态滞后生热的影响.模拟发现填料分散程度和聚合物链末端数量对模拟橡胶体系的动态滞后生热有显著的影响.模拟设计的刚-柔嵌段聚合物体系具有独特的力学强度，在高拉伸状态下，甚至会优于全刚性聚合物体系.基于模拟研究结果，设计出一种以填料为交联点，接枝环状链段并形成物理交联的新型高分子复合体系.研究结果表明，这种新型聚合物复合材料与传统物理混合材料相比，力学性能最高提升640%，生热性能降低40%.该研究结果有望为设计和制备高力学强度、低滞后生热橡胶复合材料提供一种新的途径.