关于丢番图方程(na)x+(nb)y=(nc)z(c=65,89,101)

管训贵

(泰州学院 数理学院，江苏 泰州 225300)

设

a

,

b

,

c

为两两互素的正整数且满足

a

+

b

=

c

.

对于任意的正整数

n

,丢番图方程(

na

)+(

nb

)=(

nc

)

(1)

论文考虑方程(1)中(

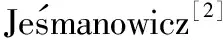
a

,

b

,

c

)=(56,33,65),(80,39,89)以及(20,99,101)的情形,得到了如下结论.

定理1

对任意的正整数

n

,丢番图方程(56

n

)+(33

n

)=(65

n

)

(2)

仅有正整数解(

x

,

y

,

z

)=(2,2,2)

.

定理2

对任意的正整数

n

,丢番图方程(80

n

)+(39

n

)=(89

n

)

(3)

仅有正整数解(

x

,

y

,

z

)=(2,2,2)

.

定理3

对任意的正整数

n

,丢番图方程(20

n

)+(99

n

)=(101

n

)

(4)

仅有正整数解(

x

,

y

,

z

)=(2,2,2)

.

1 若干引理

引理1

设正整数

a

,

b

,

c

满足

a

+

b

=

c

.

若

z

≥max{

x

,

y

},则丢番图方程

a

+

b

=

c

仅有正整数解(

x

,

y

,

z

)=(2,2,2)

.

引理2

如果方程(1)有解(

x

,

y

,

z

)≠(2,2,2),则

x

,

y

,

z

互不相同.

引理3

设

a

,

b

,

c

是两两互素的正整数且满足

a

+

b

=

c

.

若丢番图方程

a

+

b

=

c

仅有正整数解(

x

,

y

,

z

)=(2,2,2),则方程(1)没有满足

z

<

y

<

x

或

z

<

x

<

y

的正整数解.

引理4

在丢番图方程(2

uv

)+(

u

-

v

)=(

u

+

v

)

(5)

中，令

u

-

v

=

m

，

v

=

n

，gcd(

m

,

n

)=1，则(5)变成(2

n

(

n

+

m

))+(

m

(2

n

+

m

))=(2

n

(

n

+

m

)+

m

),

(6)

若

m

≡3,5(mod8)，则方程(6)仅有正整数解(

x

,

y

,

z

)=(2,2,2)

.

取

m

=3，

n

=4，可得引理5.

引理5

丢番图方程56+33=65仅有正整数解(

x

,

y

,

z

)=(2,2,2)

.

引理6

设

a

,

b

,

c

为两两互素的正整数满足

a

+

b

=

c

，且2|

b

，或者

d

(

b

)=

f

表示

b

中2的最高方幂，若

a

,

c

≡±1(mod

b/

2)，则丢番图方程

a

+

b

=

c

仅有正整数解(

x

,

y

,

z

)=(2,2,2)

.

由引理6立得引理7，8.

引理7

丢番图方程80+39=89仅有正整数解(

x

,

y

,

z

)=(2,2,2)

.

引理8

丢番图方程20+99=101仅有正整数解(

x

,

y

,

z

)=(2,2,2)

.

2 定理的证明

先证定理1.根据引理1～3和引理5，只需研究方程(2)在

n

≥2且min{

x

,

y

}<

z

x

,

y

}时的情形.

情形1

x

>

z

>

y.

此时方程(2)可化为33=

n

-(65-56

n

-)

.

(7)

由于

z

>

y

,故gcd(

n

,33)>1

.

设

n

=311

n

,

u

+

v

≥1,gcd(

n

,33)=1,此时(7)式成为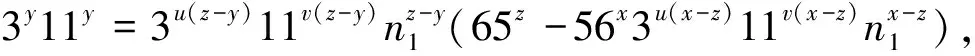

(8)

由此可见

n

=1

.

(i) 若

n

=3(

u

≥1),则

y

=

u

(

z

-

y

)

.

于是(8)式可化为563(-)=65-11

.

(9)

对(9)式取模4，有1≡(-1)(mod4),得

y

≡0(mod2)

.

对(9)式取模3，有(-1)≡(-1)≡1(mod3),得

z

≡0(mod2)

.

令

z

=2

z

,

y

=2

y

,则由(9)式得2373(-)=(65+11)(65-11)

.

注意到gcd(65+11,65-11)=2

.

① 当2|

y

时，由4|(65-11)知，23-1|(65-11)

.

若7|(65-11),则(23-1·7)|(65-11),但23-1·7>23·72=392>65-11,不可能.若7|(65+11),3|(65+11),则2⫮

z

,且有65-11=23-1

.

(10)

若7|(65+11),3⫮(65+11),则2|

z

,且有65+11=2·7

.

(11)

② 当2⫮

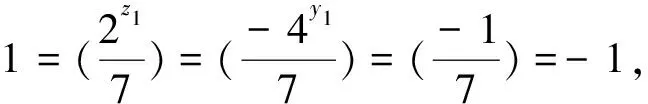
y

时，由4|(65+11)知，23-1|(65+11)

.

若7|(65+11),则(23-1·7)|(65+11),但23-1·7>23·72=392>65+11,不可能.若7|(65-11),3|(65-11),则2⫮

z

,且有65+11=23-1

.

(12)

65-11=2·7

.

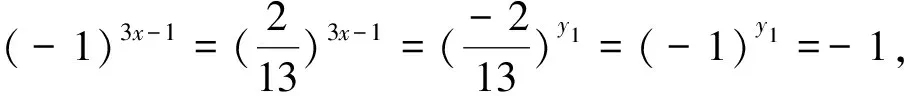
(13)

(ii) 若

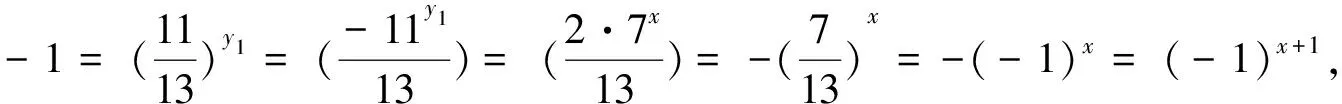
n

=11(

v

≥1),则

y

=

v

(

z

-

y

)

.

于是(8)式可化为5611(-)=65-3

.

(14)

23711(-)=(65+3)(65-3)

.

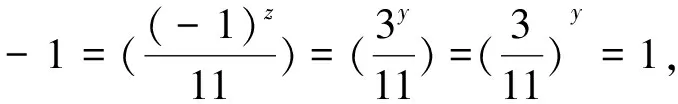
(15)

类似(i)的讨论知，(15) 式不成立，从而(14)式不成立.

(iii) 若

n

=311(

u

≥1,

v

≥1),则

y

=

u

(

z

-

y

)=

v

(

z

-

y

)

.

于是(8)式可化为563(-)11(-)=65-1

.

(16)

对(16)式取模7，有2≡1(mod7),得

z

≡0(mod3)

.

因613|(65-1),故613|(65-1),但613⫮563(-)11(-),因此(16)式不成立.

情形2

y

>

z

>

x.

此时方程(2)可化为56=

n

-(65-33

n

-)

.

(17)

设

n

=27

n

,这里gcd(

n

,14)=1,

r

+

s

≥0,则(17)式成为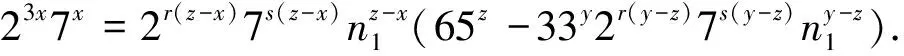

(18)

由(18)式可知

n

=1,且有65-332(-)7(-)=23-(-)7-(-)

.

(19)

(i) 若

r

=

s

=0,则由(19)式得56+33=65

.

(20)

根据引理5，方程(20)仅有正整数解(

x

,

y

,

z

)=(2,2,2),与

y

>

z

>

x

矛盾.故(20)式不成立.(ii) 若

r

=0,

s

>0,则由(19)式得

x

=

s

(

z

-

x

),且有3117(-)=65-8

.

(21)

对(21)式取模7，有2≡1(mod7),得

z

≡0(mod3)

.

令

z

=3

z

,则(21)式成为3117(-)=(65-2)(652+652+22)

.

(22)

(iii) 若

r

>0,

s

=0,则由(19)式得3

x

=

r

(

z

-

x

),且有3112(-)=65-7

.

(23)

11>11=112=121>(65+7)>65+7>65-7

不可能， 因此(23)式不成立.

(iv) 若

r

>0,

s

>0,则由(19)式得3

x

=

r

(

z

-

x

),

x

=

s

(

z

-

x

),且有332(-)7(-)=65-1

.

(24)

对(24)式取模7，有2≡1(mod7),得

z

≡0(mod3)

.

因613|(65-1),故613|(65-1),但613⫮332(-)7(-),因此(24)式不成立.定理1得证.再证定理2.根据引理1～3和引理7，只需研究方程(3)在

n

≥2且min{

x

,

y

}<

z

x

,

y

}时的情形.

情形1

x

>

z

>

y.

此时方程(3)可化为39=

n

-(89-80

n

-)

.

(25)

由于

z

>

y

,故gcd(

n

,39)>1

.

设

n

=313

n

,

u

+

v

≥1,gcd(

n

,39)=1,此时(25)式成为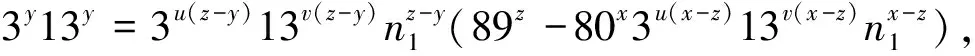

(26)

由此可见

n

=1

.

(i) 若

n

=3(

u

≥1),则

y

=

u

(

z

-

y

)

.

于是(26)式可化为803(-)=89-13

.

(27)

对(27)式取模3，有(-1)≡1(mod3),得

z

≡0(mod2)

.

对(27)式取模8，有1≡5(mod8),得

y

≡0(mod2)

.

令

z

=2

z

,

y

=2

y

,则由(27)式得2453(-)=(89+13)(89-13)

.

(28)

注意到gcd(89+13,89-13)=2,由4|(89-13)知，24-1|(89-13),但24-1>24=28=256>89-13不可能.因此(28)式不成立，从而(27)式不成立.

(ii) 若

n

=13(

v

≥1),则

y

=

v

(

z

-

y

)

.

于是(26)式可化为8013(-)=89-3

.

(29)

24513(-)=(89+3)(89-3)

.

(30)

注意到gcd(89+3,89-3)=2,有24-1|(89+3)或24-1|(89-3),但24-1>24=28=256>89+3>89-3不可能.因此(30)式不成立，从而(29)式不成立.

(iii) 若

n

=313(

u

≥1,

v

≥1),则

y

=

u

(

z

-

y

)=

v

(

z

-

y

)

.

于是(26)式可化为803(-)13(-)=89-1

.

(31)

因11|(89-1),而11⫮803(-)13(-),故(31)式不成立.

情形2

y

>

z

>

x.

此时方程(3)可化为80=

n

-(89-39

n

-),

(32)

设

n

=25

n

,这里gcd(

n

,10)=1,

r

+

s

≥0,则(32)式成为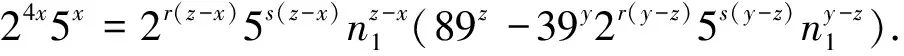

(33)

由(33)式可知

n

=1,且有89-392(-)5(-)=24-(-)5-(-)

.

(34)

(i) 若

r

=

s

=0,则由(34)式得80+39=89

.

(35)

根据引理7，方程(35)仅有正整数解(

x

,

y

,

z

)=(2,2,2),与

y

>

z

>

x

矛盾.故(35)式不成立.(ii) 若

r

=0,

s

>0,则由(34)式得

x

=

s

(

z

-

x

),且有3135(-)=89-16

.

(36)

对(36)式取模5，有(-1)≡1(mod5),得

z

≡0(mod2)

.

令

z

=2

z

,则(36)式成为3135(-)=(89+4)(89-4)

.

注意到gcd(89+4,89-4)=1,有13|(89+4)或13|(89-4),但13>13=132=169>89+4>89-4不可能.因此(36)式不成立.

(iii) 若

r

>0,

s

=0,则由(34)式得4

x

=

r

(

z

-

x

),且有

3132(-)=89-5,

(37)

若

r

=1,则

z

=5

x

,此时(37)式成为3132-5=895-5

.

易知，127|(89-5),故127|(895-5),而127⫮3132-5,故

r

≠1

.

若

r

=2,则

z

=3

x

,此时(37)式成为31322(-3)=893-5

.

易知，4519|(89-5),故4 519|(893-5),而4 519⫮31322(-3),故

r

≠2

.

于是

r

≥3

.

对(37)式取模8，有1≡(-3)(mod8),得

x

≡0(mod2)

.

再对(37)式取模3，有(-1)≡(-1)≡1(mod3),得

z

≡0(mod2)

.

令

z

=2

z

,

x

=2

x

,则(37)式成为3132(-)=(89+5)(89-5)

.

注意到gcd(89+5,89-5)=2,有13|(89+5)或13|(89-5),但13>13=132=169>(89+5)>89+5>89-5不可能， 因此(37)式不成立.

(iv) 若

r

>0,

s

>0,则由(34)式得4

x

=

r

(

z

-

x

),

x

=

s

(

z

-

x

),且有

392(-)5(-)=89-1,

(38)

因11|(89-1),而11⫮392(-)5(-),因此(38)式不成立.定理2得证.

最后证定理3.根据引理1～3和引理8，只需研究方程(4)在

n

≥2且min{

x

,

y

}<

z

x

,

y

}时的情形.

情形1

x

>

z

>

y.

此时方程(4)可化为99=

n

-(101-20

n

-)

.

(39)

由于

z

>

y

,故gcd(

n

,99)>1

.

设

n

=311

n

,

u

+

v

≥1,gcd(

n

,33)=1,此时(39)式成为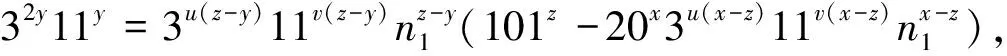

(40)

由此可见

n

=1

.

(i) 若

n

=3(

u

≥1),则2

y

=

u

(

z

-

y

)

.

于是(40)式可化为203(-)=101-11

.

(41)

对(41)式取模3,有(-1)≡(-1)(mod3),得

z

≡

y

(mod2)

.

对(41)式取模4，有1≡(-1)(mod4),得

y

≡0(mod2),故

z

≡

y

≡0(mod2)

.

令

z

=2

z

,

y

=2

y

,则由(41)式得2253(-)=(101+11)(101-11)

.

注意到gcd(101+11,101-11)=2,5|(101-11)

.

① 当2|

y

时，由4|(101-11),知22-1|(101-11)

.

此时(22-1·5)|(101-11),但22-1·5>22·5=20=202=400>101-11不可能.② 当2⫮

y

时，由4|(101+11),知22-1|(101+11)

.

若2|

z

,则3|(101+11)

.

此时101-11=2·5

.

(42)

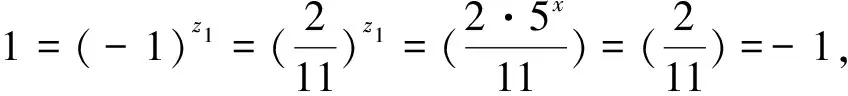
101+11=22-1,

(43)

101-11=2·5·3(-)

.

(44)

将(43),(44)两式相减得

11=22-2-5·3(-)

.

(45)

对(45)式取模3，有(-1)≡1(mod3),得2|

y

,与2⫮

y

矛盾.(ii) 若

n

=11(

v

≥1),则

y

=

v

(

z

-

y

)

.

于是(40)式可化为2011(-)=101-9

.

(46)

对(46)式取模8，有5≡1(mod8),得

z

≡0(mod2)

.

对(46)式取模5，有1≡(-1)(mod5),得

y

≡0(mod2)

.

令

z

=2

z

,

y

=2

y

,则由(46)式得22511(-)=(101+9)(101-9)

.

注意到gcd(101+9,101-9)=2,22-1|(101-9)

.

① 当2|

y

时，5|(101-9)

.

此时(22-1·5)|(101-9),但22-1·5>22·5=20=202=400>101-9不可能.② 当2⫮

y

时，5|(101+9)

.

若11|(101+9),则

101+9=2·5·11(-),

(47)

101-9=22-1

.

(48)

将(47),(48)两式相减得

9=5·11(-)-22-2

.

(49)

101+9=2·5,

(50)

101-9=22-1·11(-)

.

(51)

将(50),(51)两式相加得

101=5+22-2·11(-)

.

(52)

(iii) 若

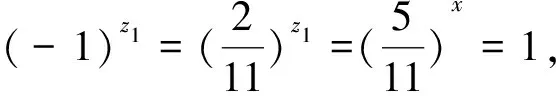
n

=311(

u

≥1,

v

≥1),则2

y

=

u

(

z

-

y

),

y

=

v

(

z

-

y

)

.

于是(40)式可化为203(-)11(-)=101-1

.

(53)

对(53)式取模3，有(-1)≡1(mod3),得

z

≡0(mod2)

.

因17|(101-1),故17|(101-1),但17⫮203(-)11(-),因此(53)式不成立.

情形2

y

>

z

>

x.

此时方程(4)可化为20=

n

-(101-99

n

-)

.

(54)

设

n

=25

n

,这里gcd(

n

,10)=1,

r

+

s

≥0,则(54)式成为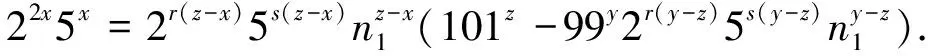

(55)

由(55)式可知

n

=1,且有101-992(-)5(-)=22-(-)5-(-)

.

(56)

(i) 若

r

=

s

=0,则由(56)式得20+99=101

.

(57)

根据引理8，方程(57)仅有正整数解(

x

,

y

,

z

)=(2,2,2),与

y

>

z

>

x

矛盾.故(57)式不成立.(ii) 若

r

=0,

s

>0,则由(56)式得

x

=

s

(

z

-

x

),且有32115(-)=101-4

.

(58)

对(58)式取模3，有(-1)≡1(mod3),得

z

≡0(mod2)

.

令

z

=2

z

,则(58)式成为32115(-)=(101+2)(101-2)

.

注意到gcd(101+2,101-2)=1,有11|(101+2)或11|(101-2),但11>11=112=121>101+2>101-2不可能. 因此(58)式不成立.(iii) 若

r

>0,

s

=0,则由(56)式得2

x

=

r

(

z

-

x

),且有32112(-)=101-5

.

(59)

(iv) 若

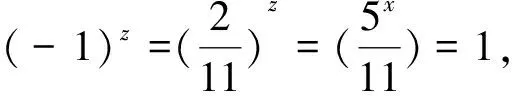
r

>0,

s

>0,则由(56)式得2

x

=

r

(

z

-

x

),

x

=

s

(

z

-

x

),且有992(-)5(-)=101-1

.

(60)

对(60)式取模3，有(-1)≡1(mod3),得

z

≡0(mod2)

.

因17|(101-1),故17|(101-1),但17⫮992(-)5(-),因此(60)式不成立.定理3得证.