基于组合预测模型对中国经济外贸依存度的预测

徐 凤，常裕琦,朱家明，胡成雨，胡金淼

(1.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233030；2.安徽财经大学 金融学院，安徽 蚌埠 233030；3.安徽财经大学 国际经济贸易学院，安徽 蚌埠 233030)

自中国2001年加入WTO以后，人民生活水平不断提高，出口企业迅猛发展，中国对外贸易额呈现连年攀升趋势.伴随美国贸易逆差再创新高,特别是对中国贸易逆差占比47%这一状况的出现，美国试图通过实施贸易保护主义措施来迫使中国对美国市场进一步开放.2018年起，美国持续发起单边贸易、保护贸易，与世界各国的多边贸易、自由贸易相抗衡.贸易摩擦的持续再次证实“中国制造2025”战略实施的必要性和紧迫性.通过分析中国对外贸易依存度指数可以看出，中国经济增长对外贸的依赖程度较高，一方面是由于国外市场的强大需求，另一方面是中国对外贸易的结构失衡、贸易目的集中以及依赖进口国外高科技产品等问题的存在.因此，贸易战的本质是改革战，实现贸易高质量发展需要国内制造业的同步配合.

针对国内经济增长对贸易的依赖度，国内许多学者已有相关研究成果.作者立足“中国制造2025”战略视角，选取1978—2018年进出口贸易数据，对2019—2025年的中国经济增长进行预测，进而对中国贸易依存度进行测度和研究.在预测方法的选择上，考虑到时间序列数据的波动性，选取存在反馈和记忆的NARX(nonlinear autoregressive with exogenous inputs)动态神经网络和拟合效果较好的ARIMA(autoregressive integrated moving average model)自回归移动平均模型进行单项预测分析.为了进一步提高预测精度，再以NARX动态神经网络和ARIMA自回归移动平均模型建立组合预测模型.

1 研究思路和数据来源

为精确获取中国经济发展对外贸易依赖度，作者选取1978—2018年的41组年度数据，分别运用NARX动态神经网络和ARIMA模型对2019—2025年中国的进口总量、出口总量和GDP进行预测，利用算式“对外贸易依存度=(进口总量+出口总量)/GDP×100%”，可得到未来7年对外贸易依存度.为了提高预测模型的精确度，以两种单项模型进一步建立组合预测模型.作者选择1978—2008年的数据为基础数据，对1991—2018年的指标进行预测.通过与真实数据进行对比及计算相对误差，来评价模型的性能和预测能力.作者选取的数据均来自中国国家统计局和Wind金融数据终端，构造时间序列，使用MATLAB和R软件对3个指标进行拟合预测，如图1所示.

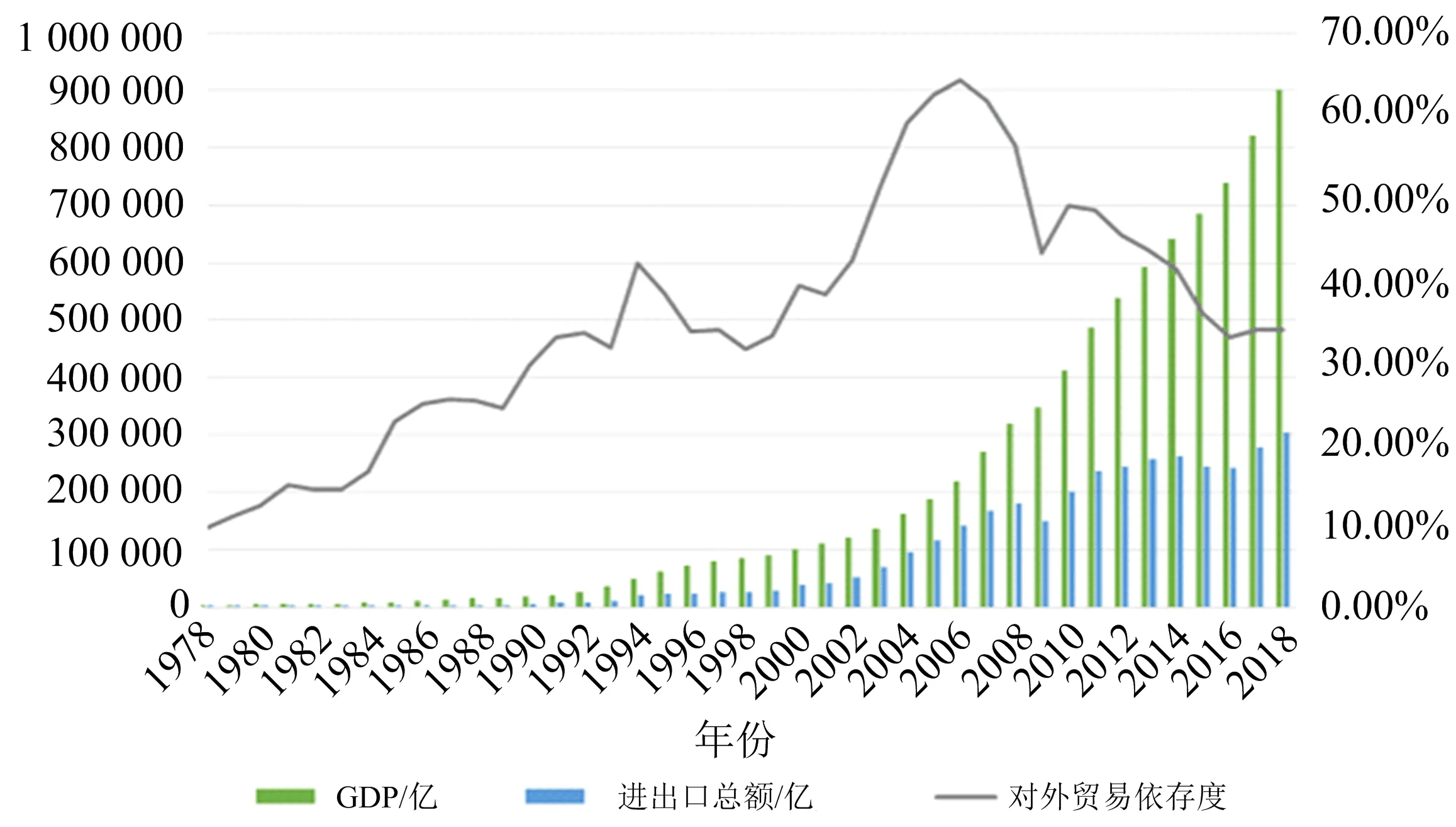
图1 中国1978—2018年GDP、进出口总量和对外贸易依存度组合图

2 基于NARX神经网络的对外贸易依存度测度和研究

2.1 NARX神经网络模型

为预测未来对外贸易依存度的变化趋势，采用NARX神经网络进行预测.NARX神经网络是基于带外源输入的非线性自回归神经网络，可表示为

y

(

t

)=

f

{

u

(

t

-

D

),…,

u

(

t

-1),

u

(

t

),

y

(

t

-

D

),…,

y

(

t

-1)}，其中:

u

(

t

),

y

(

t

)分别是该网络在

t

时刻的输入和输出；

D

为输入时延的最大阶数；

D

为输出时延的最大阶数；

u

(

t

-

D

),…,

u

(

t

-1)为相对于

t

时刻的历史输入；

y

(

t

-

D

),…,

y

(

t

-1)为相对于

t

时刻的历史输出；

f

为网络拟合得到的非线性函数.

NARX神经网络结构包含输入层、隐含层和输出层.输入层节点数根据输入值个数设定，输出层节点数根据预测值个数设定.通过合理设定隐含层层数和节点数，构建NARX神经网络.NARX神经网络与反向传播神经网络的训练方法类似，是一种动态神经网络.

2.2 NARX模型的建立

作者基于神经网络训练中已知期望的输出，可建立如图2所示的Series-Parallel神经网络模式，该模式能够将期望输出反馈到输入端，预测效果更准确.在应用模型对3个指标进行预测和分析前，先确定外部输入为2，输出为1，模型的延时阶数为12.模型基本结构如图3所示.

图2 Series-Parallel神经网络模式

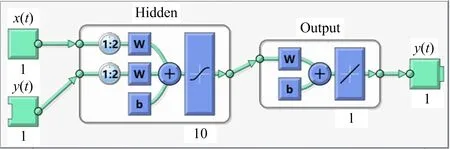
图3 NARX动态神经网络结构

通过定义相关函数，建立非线性自回归模型后，作者对NARX神经网络的训练效果进行分析，如图4,5所示.由图4可知，NARX神经网络在训练次数0～6期间迅速下降，在训练12次后验证集误差上升，证明训练可以结束，此时整个数据集的误差为5.136 4×10

.

由图5的拟合效果可以看出，作者设定的神经网络对数据的拟合效果良好，其中训练集的拟合优度为99.98%，测试集的拟合优度为98.36%，验证集的拟合优度为82.63%.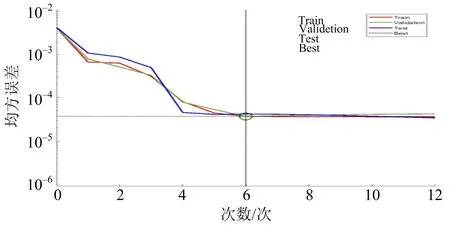

图4 NARX神经网络训练图

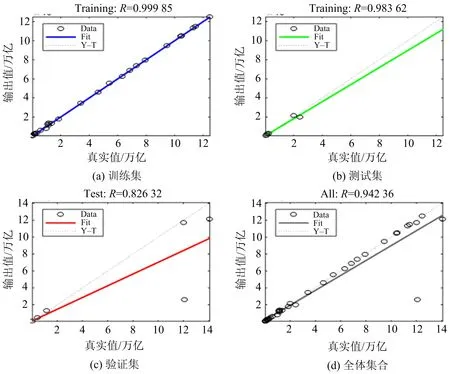
图5 NARX神经网络拟合优度

2.3 基于NARX模型的预测和系数分析

经过上文对神经网络训练和预测效果的检验分析，模型可以用来对3项指标进行预测.作者基于1978—2018年共41组年度基础数据，对2019—2025年中国贸易进口总量进行预测，预测值见表1.

表1 基于NARX神经网络预测中国2019—2025年贸易进口总量 亿元

同样，使用NARX动态神经网络模型对中国2019—2025年贸易出口总量以及生产总值GDP进行拟合及预测，拟合的模型及预测结果如表2所示.

表2 基于NARX神经网络预测中国2019—2025年出口总量和GDP 亿元

从预测结果可见，2019—2025年，中国的国民生产总值不断增加，贸易额仍然呈增长趋势，但增速放缓，并存在一定的波动.结合NARX动态神经网络模型的预测结果及公式，计算2019—2025年对应的外贸依存度指数预测值，结果见表3.

表3 基于NARX模型预测中国2019—2025年对外贸易系数值

通过上述分析，得到基于NARX动态神经网络的中国对外贸易系数值，可看出2019—2025年中国经济发展对贸易的依赖程度逐渐下降.

3 基于ARIMA模型的对外贸易依存度测度和研究

3.1 ARIMA模型

ARIMA模型的原理是将非平稳时间序列转化为平稳时间序列，然后对因变量的滞后值以及随机误差项的现值和滞后值进行回归建立模型.通过描述当前值与历史值之间的关系，用变量自身的历史时间数据对自身进行预测.采用ARIMA模型时，要先了解时间序列的平稳性，只有平稳的时间序列才可以进行ARIMA模型的拟合.有

其中：

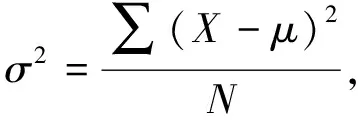
σ

为总体方差，X为变量，

μ

为总体均值，

N

为总体数量.ARIMA(

p

，

d

，

q

)中：

p

为自回归项数，

d

为使之成为平稳序列所做的差分次数(阶数)，

q

为滑动平均项数.ACF(autocorrelation function)自相关系数能决定

q

的取值，PACF (partial autocorrelation function)偏自相关系数能够决定

q

的取值.根据数据平稳性选择差分次数，当选择差分次数为1时，若数据仍为非平稳时间序列，则可以选2为差分次数，一般选择2即可得到平稳序列.

p

阶自回归过程的公式为

其中：

y

是当前值，

μ

是常数项，

p

是阶数，

γ

是自相关系数，

ε

是误差项，

y

-为前

i

天的观测值.

q

阶自回归过程的公式为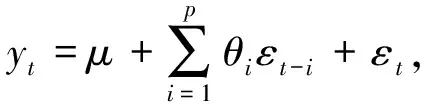

其中：

θ

为自相关系数，

ε

-是误差项滞后

i

期.根据R软件自动选择

q

阶，对

p

阶数增减一定阶数作为备选模型，对比模型的AIC值，根据最小信息准则，确定最优模型.

3.2 ARIMA模型的建立

应用ARIMA模型进行预测之前，采用时序图法以及单位根检验法对序列进行平稳性检验.将中国1978—2018年的进口贸易额数据导入R软件，得到序列趋势如图6所示.

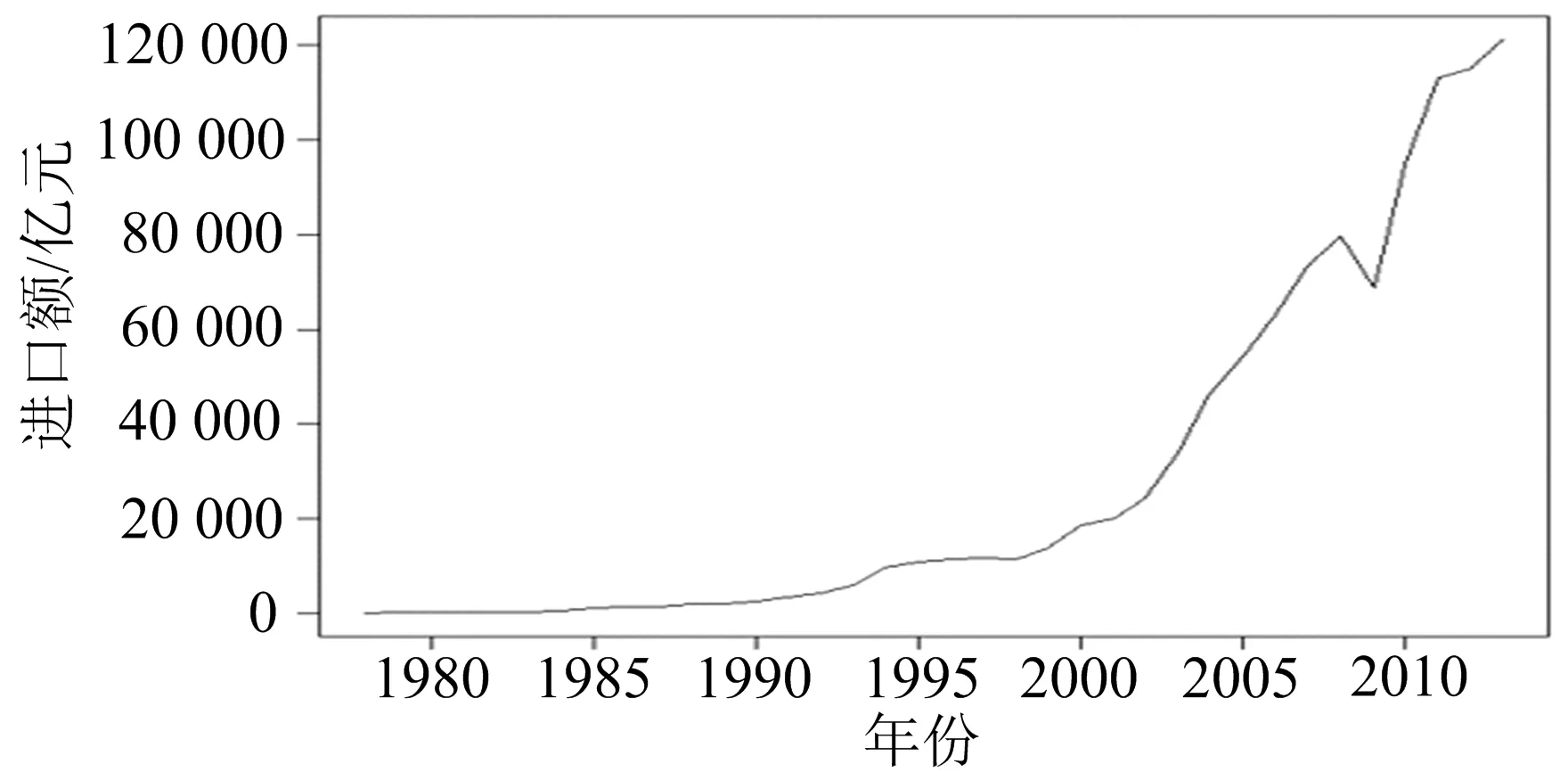
图6 进口贸易额时序图

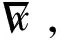
表4 3种类型单位根(ADF)的检验结果

图7 差分后序列的ACF，PACF图

从图7可见，序列自相关系数是1阶截尾而偏自相关系数是拖尾，由此初步选定ARIMA(0,2,1)模型，而R软件自带函数则自动确定ARIMA(0,2,2)为优选模型.为了更精确地拟合模型，将ACF，PACF均视为拖尾，那么可以选择的备选模型是ARIMA(1,2,1)和ARIMA(2,2,1)，结合残差平方和以及信息最小准则，可以确定出最优模型.备选模型分别为AR1(auto regression model 1)，AR2(auto regression model 2)，MA1(moving average model 1)，MA2(moving average model 2)，AIC(akaike information criterion)，如表5所示.

表5 备选模型及参数表

通过备选模型的参数表，发现ARIMA(0,2,2)的AIC值最小，为678.90，根据最小信息准则，确定该模型为最优模型.

3.3 基于ARIMA模型的预测和系数分析

利用ARIMA(0,2,2)及1978—2018年共41个年度数据，对2019—2025年中国贸易进口总量进行预测，预测值见表6.

表6 基于ARIMA模型预测中国2019—2025年进口总量 亿元

同样，使用ARIMA自回归移动平均模型对中国贸易出口总量以及生产总值GDP进行拟合及预测，拟合的模型及预测结果见表7.

表7 基于ARIMA模型预测中国2019—2025年出口总量和GDP 亿元

由表7可以看出，未来7年内中国贸易出口总量以及GDP将以一定速率稳定增长，预测数值可为中国政府制定相关经济政策及建设规划提供参考.结合ARIMA模型预测结果以及根据贸易依存度公式，可以计算出2019—2025年中国对外贸易依存度指标的预测值，结果见表8.

表8 基于ARIMA模型预测中国2019—2025年对外贸易系数值

通过表8可以清晰地看出，中国对外贸易依存度预测值逐年递减.一方面由于中国经济实力的迅速发展，GDP数值呈稳定增长；另一方面，随着中国科技实力的增强，对外进口的需求正在慢慢降低，反而转变为出口导向型国家.因此通过公式也可以看出中国对外贸易的依赖性正逐年降低.

4 基于组合预测模型的对外贸易依存度测度和研究

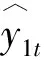
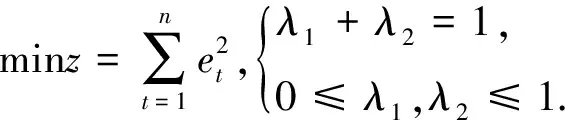
利用拉格朗日乘数法，求得组合预测模型的最优组合权重为

根据组合预测模型和求得的最优组合权重，代入1991—2018年对外贸易依存度的实际值和两种单项预测数值，计算得出预测模型的组合权重为

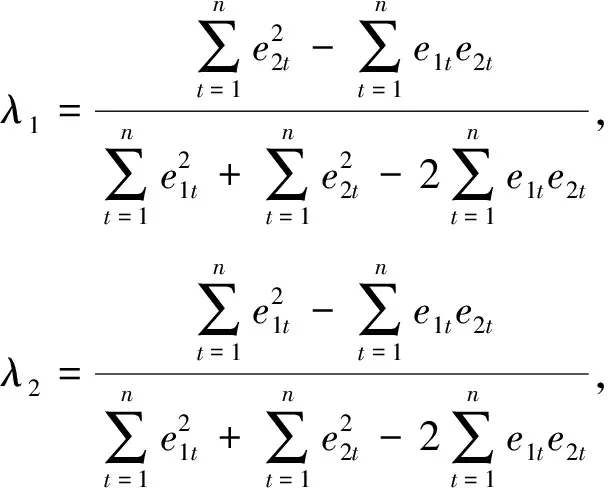
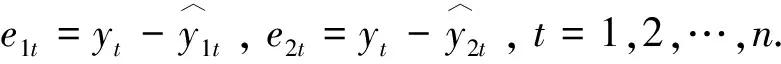
λ

=0

.

597,

λ

=0

.

403.为了检验组合预测模型是否有效，按照预测效果评价原则，选择文献[17]中常规的误差指标作为衡量预测精度的指标体系，则NARX，ARIMA模型和组合预测模型的各个精度评价指标结果见表9.由表9的预测效果评价指标体系可以看出，组合预测的各项误差指标值均低于两种单项预测模型的误差指标值，组合预测模型的预测精度更高，更适用于预测中国对外贸易依存度.用组合预测模型对中国2019—2025年对外贸易依存度进行预测，预测结果见表10.通过表10可以看出，未来7年中国经济发展对贸易的依赖程度逐渐下降.中国对外贸易依存度预测值逐年递减，一方面由于中国经济实力的迅速发展，国内消费需求大幅增加；另一方面，随着中国科技实力的增强，对外加工贸易比重大幅下降，劳动密集型产品的产量大幅下降.

表9 两种单项预测和组合预测模型预测效果评价指标体系

表10 基于组合模型预测中国2019—2025年对外贸易依存度数值

5 结束语

作者以NARX动态神经网络和ARIMA为单项预测模型，建立误差平方和最小的组合模型，预测中国经济对外贸的依存度.研究结果表明，2019—2025年中国进出口贸易额仍会较快增长，但对外贸易依存度指数值将呈下降趋势.