基于IBASIF算法的电压电流双环控制器的参数整定

于永进，胡向前，王云飞，魏 哲

(1.山东科技大学 电气与自动化工程学院，山东 青岛 266590；2.国网技术学院，山东 济南 250002；3.国网山东电力公司 检修公司，山东 济南 250118)

微电网具有高效利用可再生能源、整合分散资源的优势，发展大规模微电网为大势所趋.分布式电源通过逆变器将直流转换为交流，这对电压电流信号的质量和响应速度提出了更高要求.电压电流双环控制器是逆变器的重要构成之一，它决定了系统信号输出的稳定性，因此对电压电流双环控制器的研究具有重要意义.

电压电流双环控制器的电压控制环采用比例-积分(proportion integration，简称PI)控制器、电流控制环采用比例(proportion，简称P)控制器.不少研究人员对比例-积分-微分(proportion integration differentiation，简称PID)控制器的参数整定问题开展了研究.文献[1]提出利用极点配置法对PI控制器的参数进行整定，但该方法忽略了零点对系统的影响，导致静态性能下降.文献[2]根据传递函数的幅频特性给参数设定一个取值范围，然后在此范围寻找合适参数，但本质上还是人工寻优，且参数精度不够.文献[3]利用天牛须搜索(beetle antennae search，简称BAS)算法对典型PID控制器参数进行整定，但天牛种群的扩大增加了寻优的时间.文献[4]提出一种应用于双馈风机控制系统的PI参数优化方法，利用极点配置法寻找初值后，再用免疫遗传算法进行寻优，但局部搜索能力差，后期搜索效率低.文献[5]首先推导出电压电流双闭环模型的传递函数，然后利用算法对传递函数进行迭代寻优，但模型的寻优时间较长.文献[6]采用频域响应方法对控制器参数进行整定，但其本质上是在划定的范围寻找近似值.

针对传统参数整定方法过程复杂、准确度低等问题，笔者提出基于加入感性适应度的改进天牛须搜索(the improved beetle antennae search with inductive fitness，简称IBASIF)算法的电压电流双环控制器的参数整定方法.运用改进算法对闭环系统的PI和P控制器进行参数寻优；利用Halton序列使天牛种群在初始化阶段均匀分布，避免漏掉最优解，提高算法的寻优精度；改进超限回收机制，提高算法的收敛效率和寻优速度；采用稳定适应度和感性适应度双目标寻优，使IBASIF算法在提高寻优效率的同时使系统的输出阻抗更接近感性，提高系统的稳定性.

1 电压电流双环控制器

以低压微电网下垂控制中的典型电压电流双环控制器为例进行分析.电压电流双环控制器有两种类型：电压-电感电流型及电压-电容电流型.该文采用电压-电容电流型.

1.1 结构分析

1.1.1

LC

滤波器为了消除逆变器开合产生的谐波，需在线路中增加

LC

滤波器

.LC

滤波器结构如图1所示.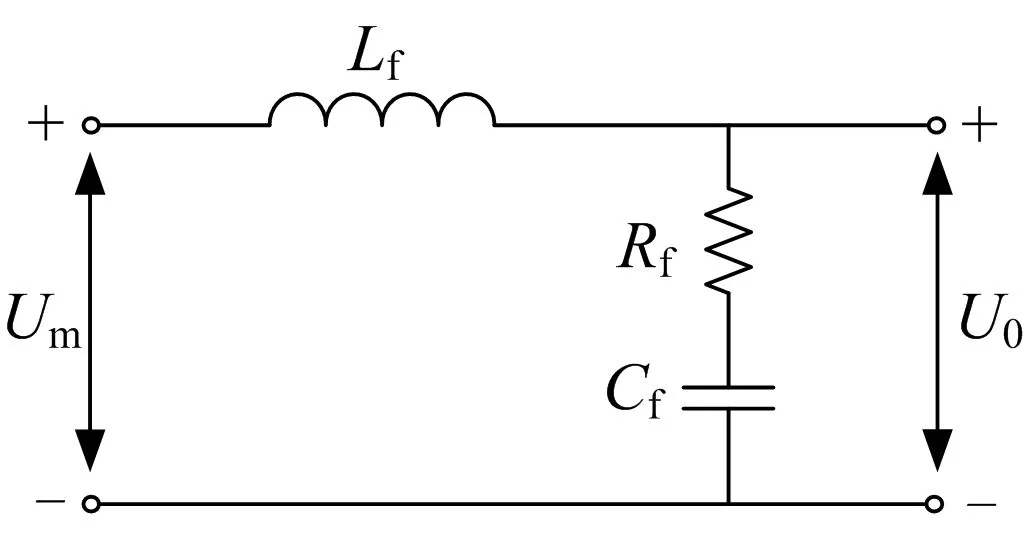

图1 LC滤波器结构

图1中，

U

为输入电压，

U

为输出电压，

LC

滤波器的传递函数为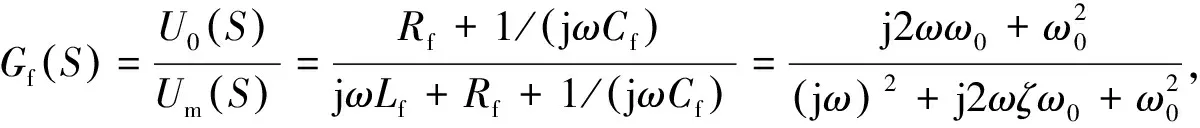

(1)

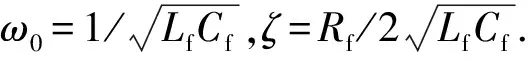
LC

滤波器的谐振频率为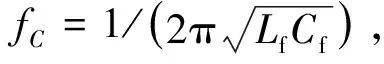

(2)

且满足

10

f

≤

f

≤

f

/

10,

(3)

其中：

f

为基波频率，

f

为正弦脉宽调制(sinusoidal pulse modulation,简称SPWM)载波频率.

1.1.2 双环控制器

电压电流双环控制器的电压控制环采用PI控制器，电流控制环采用P控制器，其结构如图2所示.

图2 电压电流双环控制器结构

图2中，

K

为电压控制环的比例系数，

K

为电压控制环的积分系数，

K

为电流控制环的比例系数，

K

为逆变器SPWM的增益.

电流控制环的传递函数为

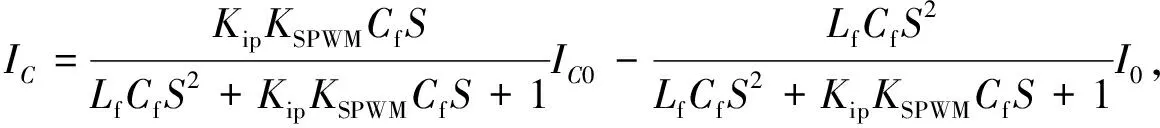
(4)

其中：

I

0，

I

分别为双环控制器的输入、输出电流.

电压控制环的传递函数为

U

=

G

(

S

)

U

-

Z

(

S

)

I

,

(5)

其中：

U

，

U

分别为双环控制器的输入、输出电压；

G

(

S

)，

Z

(

S

)分别为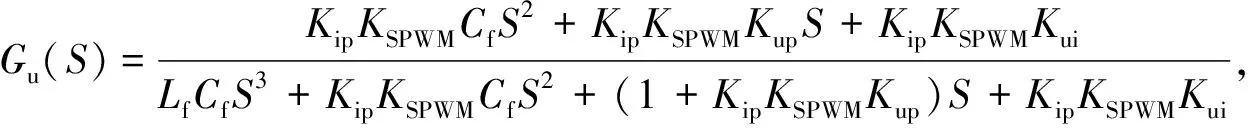

(6)

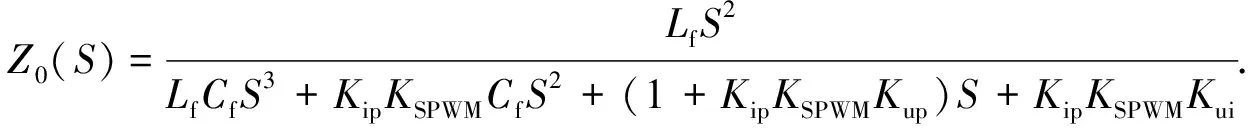
(7)

由式(6)和(7)可知，滤波电感

L

和滤波电容

C

的值不变时，

G

(

S

)和

Z

(

S

)仅由

K

，

K

，

K

决定.系统电流跟踪电压的效果由

G

(

S

)决定，系统的阻抗特性由

Z

(

S

)决定，因此能否对

K

，

K

，

K

进行合理整定直接影响逆变器输出信号的质量.

1.2 目标函数

该文将稳定适应度和感性适应度作为寻优的双目标、二者之和(总适应度)作为目标函数，其中稳定适应度在仿真模型中实现、感性适应度在算法中实现.

1.2.1 稳定适应度

该文的PI和P控制器结构如图3所示.

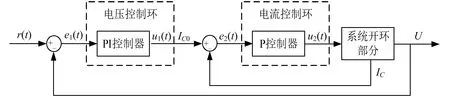
图3 该文的PI和P控制器结构

图3中，

r

(

t

)为控制器的输入信号；

e

(

t

)，

e

(

t

)分别为电压、电流环的输入信号；

u

(

t

)，

u

(

t

)的表达式分别为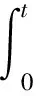

(8)

u

(

t

)=

K

e

(

t

)

.

(9)

如果控制器参数整定合理，则控制信号使误差减小，达到控制要求.控制性能用稳定适应度描述，其表达式为

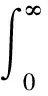
(10)

1.2.2 感性适应度

低压微电网下垂控制的前提是系统的等效输出阻抗呈感性.为使寻优参数符合要求，需加入计算感性适应度的环节.下面给出感性适应度的定义式.

利用命令

[mag,phase,

ω

]=bode[

Z

(

S

),

ω

]

(11)

得到角速度为

ω

时等效输出阻抗的幅值mag和相位phase.要使输出阻抗为感性，需

ω

=100 rad·s时相位phase=90°.

感性适应度定义式为

D

=phase-90°

.

(12)

2 IBASIF算法

2.1 天牛须搜索算法

相对于粒子群优化(particle swarm optimization，简称PSO)算法，BAS能够以较少的种群数目实现全局搜索，不知函数的具体形式也可实现高效寻优.天牛须搜索算法步骤为：

(1) 随机确定天牛头部方向单位向量的坐标,其表达式为

(13)

其中：

k

为空间维度，rand(,)为随机函数.(2) 确定天牛左右两须的位置，第

t

次迭代时天牛左右两须的位置坐标分别为

x

=

x

-

d

b

,

(14)

x

=

x

+

d

b

,

(15)

其中：

t

为迭代次数，

d

为天牛两须的距离.

(3) 计算适应度，然后沿适应度易解的方向将位置坐标更新为

x

=

x

-1+

δ

b

sign(

f

(

x

)-

f

(

x

)),

(16)

其中：

δ

为搜索步长，sign()为符号函数，

f

()为目标函数.

(4) 将天牛两须的距离和步长分别更新为

d

=

ηd

-1+0

.

01,

(17)

δ

=

ηδ

-1,

(18)

其中：

η

为缩小系数，通常取为0.95.

2.2 改进的天牛须搜索算法

为提高算法的寻优精度，改进的天牛须搜索(the improved beetle antennae search,简称IBAS)算法引入Halton序列使天牛种群初始时能全局均匀分布，降低漏掉最优解的概率.为提高算法的寻优效率，对超限种群的处理机制进行改进，以提高迭代收敛的概率.

2.2.1 改进种群分布

Sobol，Halton，Faure序列均是拟蒙特卡洛序列.文献[15]在量子粒子群算法中使用Sobol序列消除了粒子重叠现象，该文将Halton序列应用于天牛种群的初始化.图4为基数

a

=2时生成Halton序列的示意图.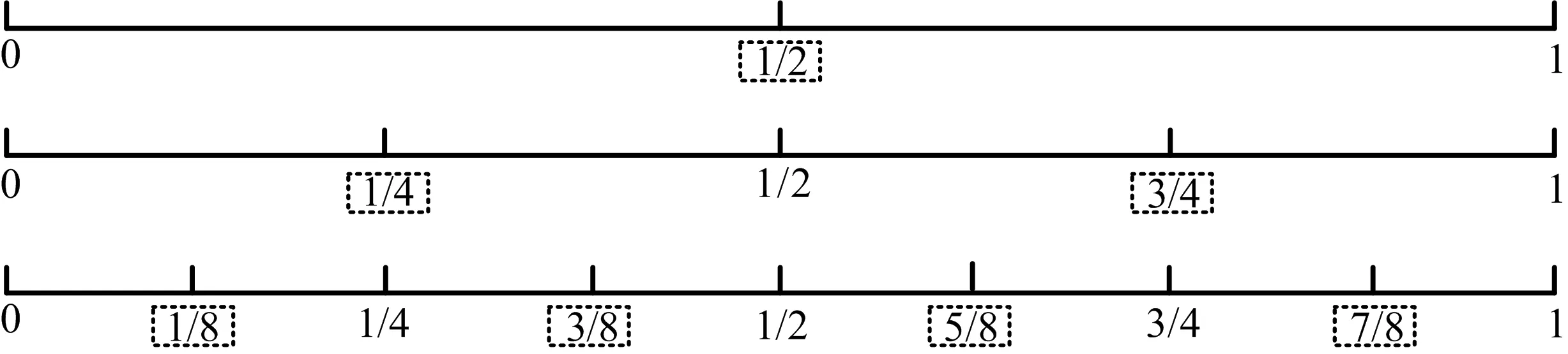

图4 a=2时生成Halton序列的示意图

图5为随机序列及Halton序列在2维空间生成粒子的情况.由图5可看出，相对于随机序列，Halton序列生成的粒子分布更均匀.

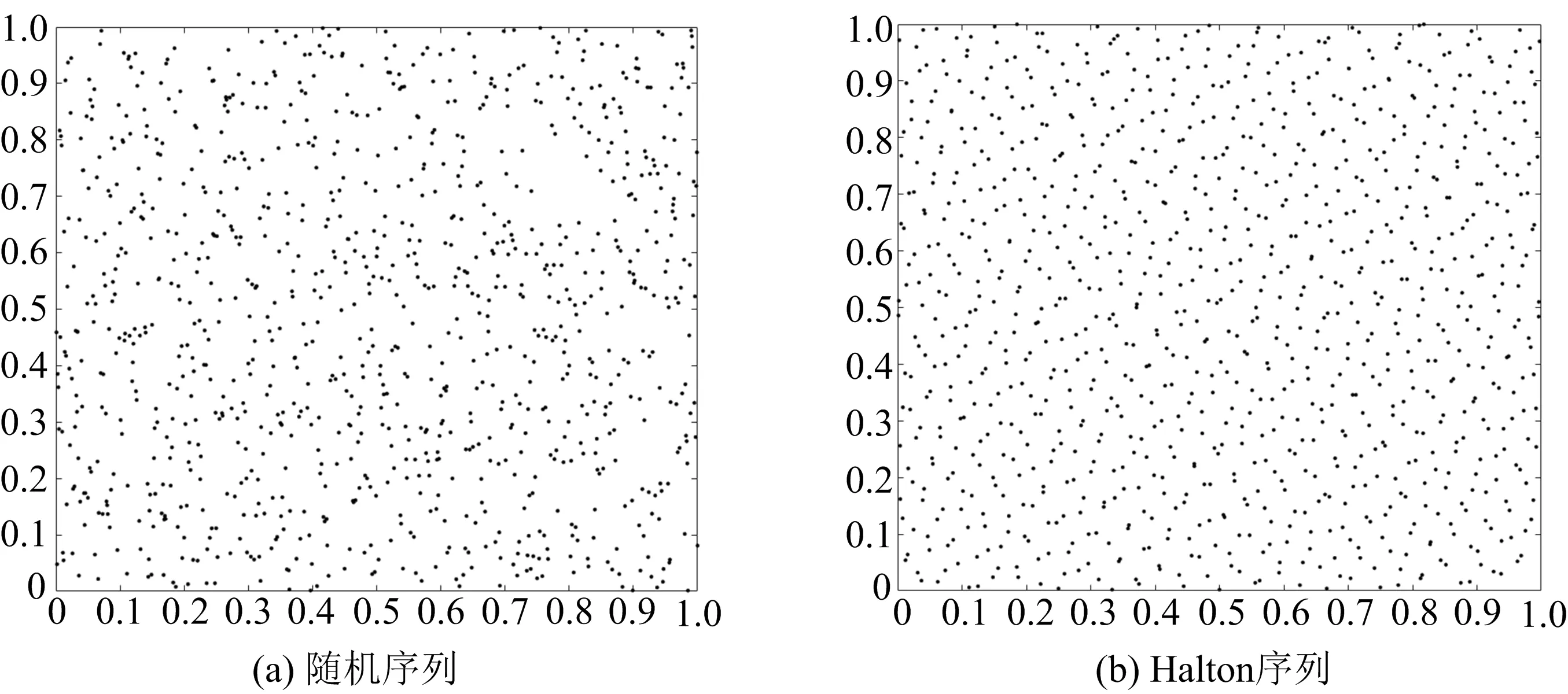
图5 随机序列及Halton序列在2维空间生成粒子的情况

Halton序列确定的天牛位置坐标为

x

=rand(,)×(

x

-

x

)+

x

,

(19)

其中：

x

，

x

分别为天牛位置坐标的最大、最小值.

2.2.2 改进超限回收机制

超限种群的处理机制有两种：第1种是对超过坐标限制的种群直接舍弃；第2种是将超过坐标上限的种群回收至上限边界处，超过坐标下限的种群回收至下限边界处.该文在第2种方法的基础上对回收机制进行改进：当天牛某维度坐标超限时，就将该维度坐标回收至当前最优总适应度坐标附近，其余维度坐标不变，这就增大了寻得最优适应度的概率，提高了收敛的效率.

当

k

维超限的天牛位置坐标

x

(1,

k

)>

x

(1,

k

)或

x

(1,

k

)<

x

(1,

k

)时，超限的天牛位置坐标回收至

x

(1,

k

)=

x

(1,

k

)+0

.

5,

(20)

其中：

x

(1,

k

)为当前最优总适应度对应的位置坐标.

2.3 IBASIF算法

在IBAS算法的基础上，笔者加入感性适应度得到IBASIF算法，该算法流程如图6所示.

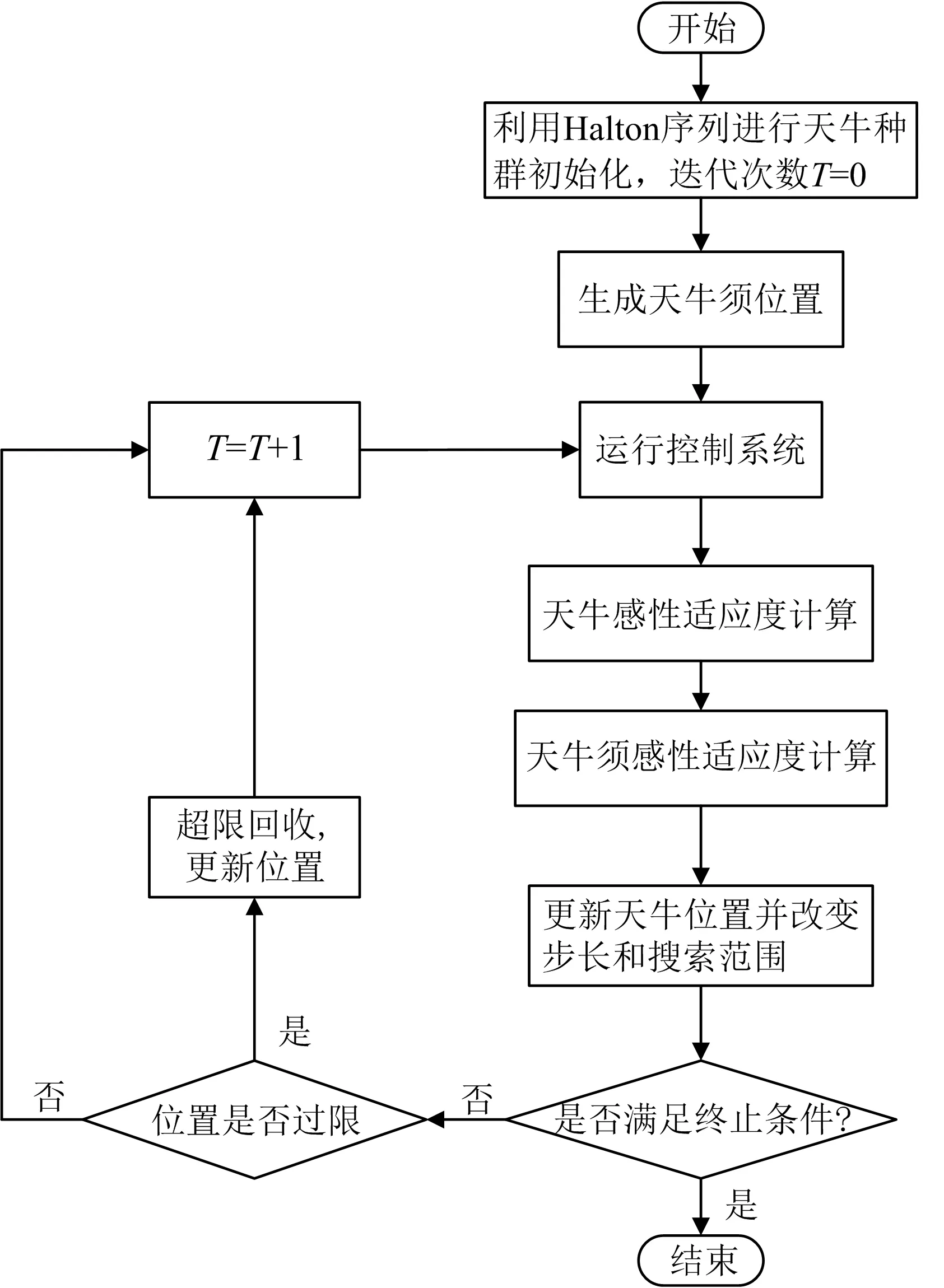
图6 IBASIF算法流程图

3 仿真分析

运用Matlab对基于IBASIF算法的电压电流双环控制器的参数整定方法进行仿真实验，验证该方法的有效性和可行性.

3.1 仿真模型

电压电流双环控制器仿真模型如图7所示.

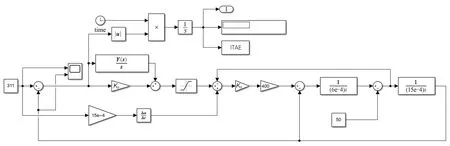
图7 电压电流双环控制器仿真模型

设置的仿真模型参数如表1所示.

表1 仿真模型参数

3.2 稳定适应度分析

算法的稳定适应度收敛特性越好，整定的参数就越能以较快的速度接近最优值.采用PSO，BAS，IBAS，IBASIF算法，对电压电流双环控制器的参数进行整定，4种算法的稳定适应度收敛特性曲线如图8所示.

图8 稳定适应度收敛特性曲线

由图8可知，第1次迭代时IBAS和IBASIF的稳定适应度分别为1.310 2和1.351 8，而PSO和BAS的分别为2.964 9和1.965 0.因此，相对PSO，BAS，在迭代初期两种改进天牛须搜索算法就能将参数限制于更靠近最优值的范围.

4种算法的最优稳定适应度如表2所示.

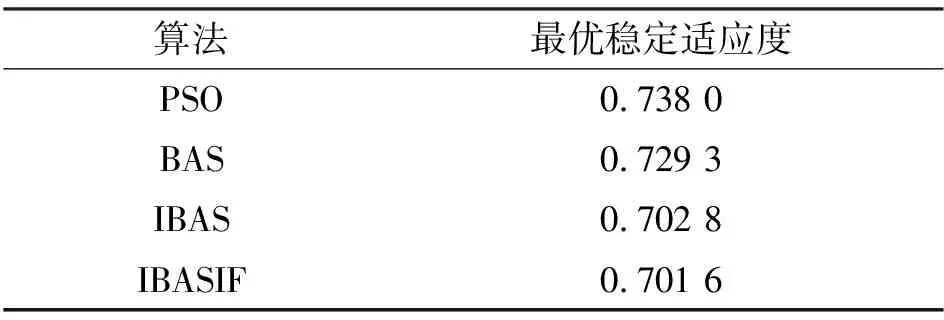
表2 4种算法的最优稳定适应度

从表2可知， IBAS和IBASIF的最优稳定适应度分别为0.702 8和0.701 6.因此，相对于其他3种算法，IBASIF算法的稳定适应度收敛特性更好、参数整定速度更快.

3.3 感性适应度分析

算法的感性适应度越小，系统等效输出阻抗越接近感性，系统稳定性越高.将表3中的

K

，

K

，

K

的整定结果代入

Z

(

S

)的传递函数，得到如图9所示的幅相特性曲线.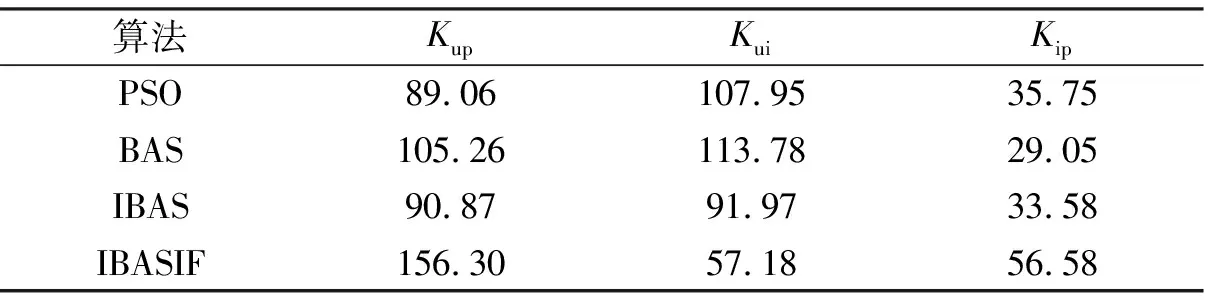

表3 4种算法的参数整定结果

图9 幅相特性曲线

由图9可知， IBASIF在角速度

ω

=100 rad·s(频率50 Hz)时的相位比其他3种算法更接近90°.根据式(12)可得到4种算法对应的感性适应度

D

，进而由式

A

=

J

+

D

(21)

得到总适应度.表4为4种算法的感性适应度和总适应度.

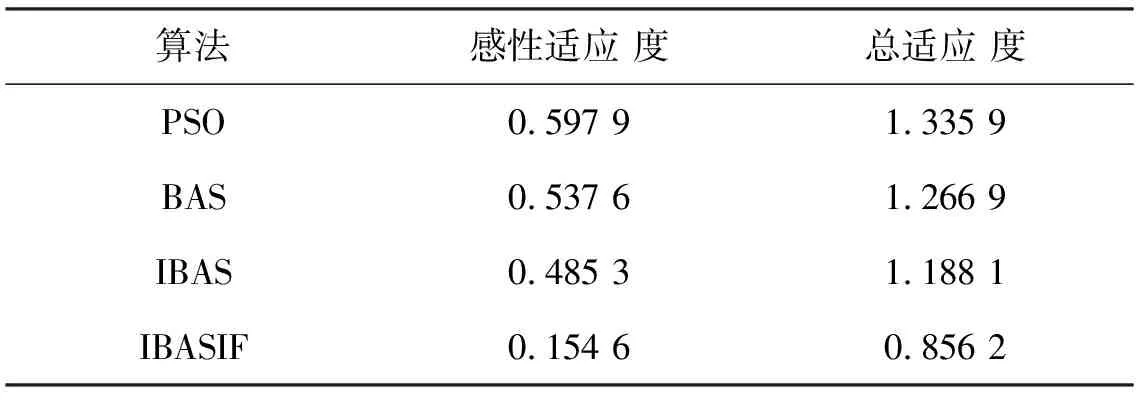
表4 4种算法的感性适应度和总适应度

由表4可知：IBASIF的感性适应度为0.154 6，而其他3种算法均在0.5左右； IBASIF的总适应度以0.856 2优于其他3种算法.因此，IBASIF在快速、准确整定参数的同时能使系统的等效输出阻抗更接近感性.

3.4 系统稳定性分析

为验证感性输出阻抗条件下系统的稳定性，将IBAS和IBASIF整定的控制器参数分别应用于微电网系统进行仿真分析.微电网系统参数设置如表5所示.

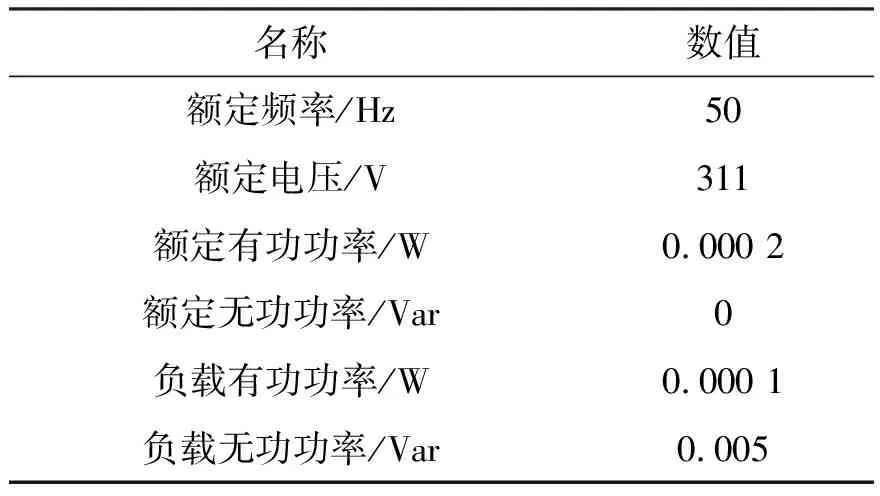
表5 微电网系统参数

仿真时间设置为1 s；负载1,2的容量相同；负载1始终与微电网相连，负载2于0.3 s投入、0.6 s切除.2种算法的系统频率如图10所示.

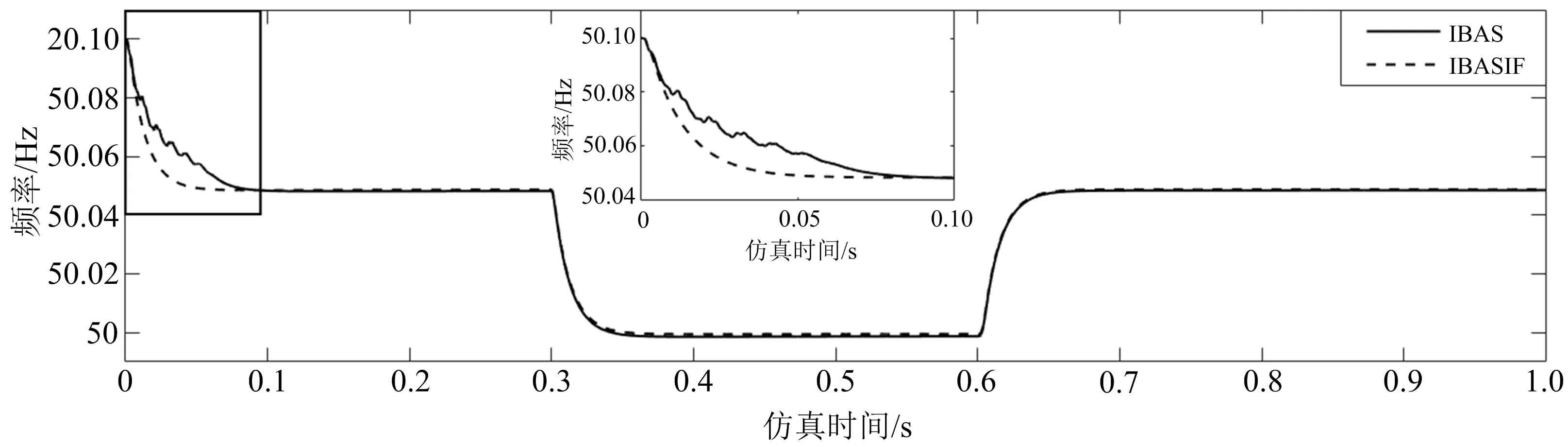
图10 2种算法的系统频率

从图10可看出：在0～0.1 s IBAS的系统频率有较大扰动，过渡不够平滑，而IBASIF的系统频率过渡比较平滑；在0.3～0.6 s由于负载2的投入导致二者频率均下降，但IBASIF的频率偏移量相对较小.

以

A

相为例，2种算法的系统输出电压如图11所示.

图11 2种算法的系统输出电压

从图11可看出，在0～0.1 s IBAS的电压波动较大，与额定电压的差最大达100 V，而IBASIF的电压波形较平滑.

以上分析表明，在微电网系统启动或负荷发生投切变化时，IBASIF能使系统的频率和电压保持在额定值附近，其所整定的参数能为下垂控制提供更好的感性条件，进而提升系统的稳定性.

4 结束语

为解决控制器参数整定耗时费力问题，笔者提出了基于加入感性适应度的改进天牛须搜索算法的电压电流双环控制器参数整定方法.运用Matlab仿真软件对PSO，BA，IBAS，IBASIF算法的稳定适应度、感性适应度及系统的稳定性进行了对比，结果表明：IBASIF能使系统的等效输出阻抗更接近感性，其所整定的参数能提升系统的稳定性.