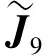由三组谱数据重构一类伪Jacobi矩阵

雷英杰，郭雪娟

(中北大学 理学院，山西 太原 030051)

Jacobi矩阵的逆特征值问题在数学及其他领域有着广泛应用，如振动方程、航空动力等领域.Jacobi 矩阵是对称三对角矩阵，形式为

论文研究以下一类伪Jacobi矩阵的逆特征值问题

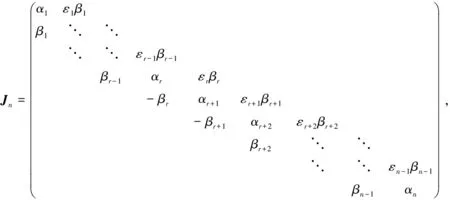
(1)

由于此类矩阵不能通过相似变换化为Jacobi矩阵，故称之为伪Jacobi矩阵.该伪Jacobi矩阵的研究主要应用于非Hermitian量子物理领域中.近年来，人们对伪Jacobi矩阵逆特征值问题的研究也取得了一些进展.

规定

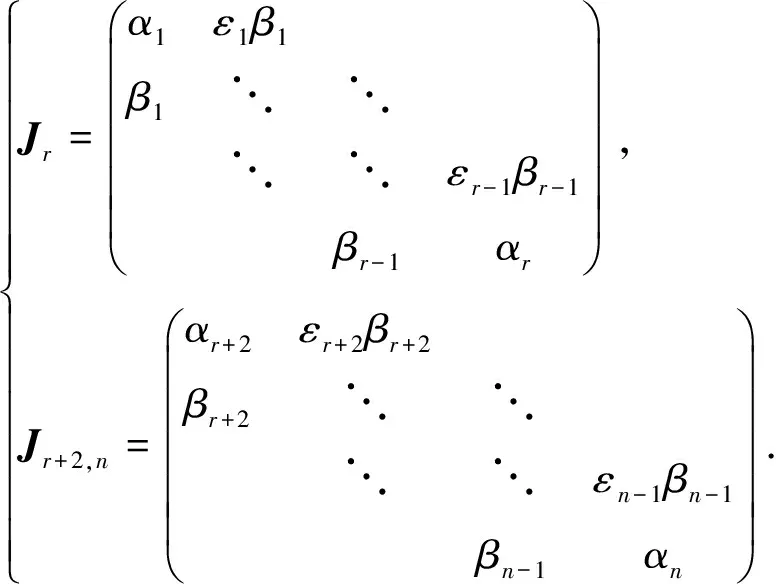
(2)

约定

σ

()记为矩阵的谱，考虑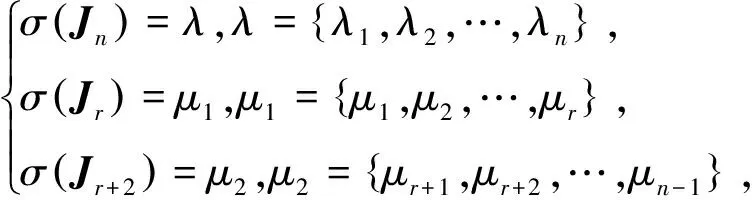

(3)

论文首先分析的谱性质；然后研究此类伪Jacobi矩阵的一些逆特征值问题，给出其有解的充分必要条件和数值算法；最后，给出数值实例予以验证.

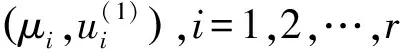
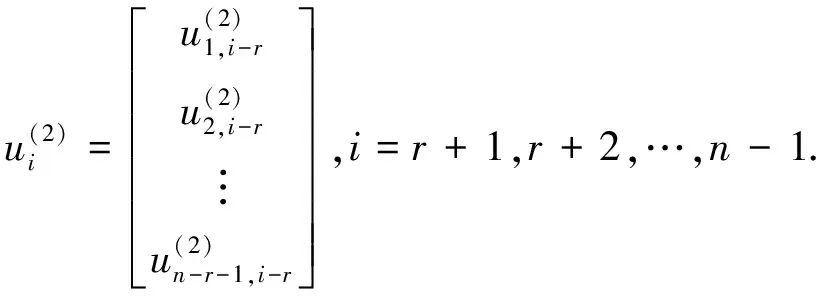
1 伪Jacobi矩阵谱的性质

引理1

已知是一个

m

阶Jacobi矩阵,其次对角元为

γ

,

γ

,…,

γ

-1

.

令特征值

ξ

对应的单位特征向量为

s

,

i

=1,2,…,

m

，则

χ

′(

ξ

)

s

1

s

,=

γ

γ

…

γ

-1,

i

=1,2,…,

m

，其中：

χ

′(

ξ

)是

χ

(

ξ

)的导数,

χ

(

ξ

)=det(

ξ

-),

s

1和

s

,分别是

s

的第一个和最后一个分量.

定理1

已知矩阵∈

J

(

n

,

ε

,

β

)且和+2,如(2)所示，

μ

和

μ

如(3)所示，则对于任意的

j

=1,2,…,

n

-1，当且仅当

μ

∈

σ

()∩

σ

(+2,)时,

μ

∈

σ

()

.

根据前面的介绍可知和正交且满足

从而矩阵=⊕

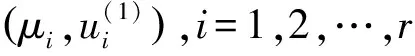
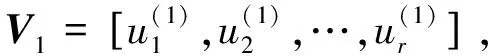
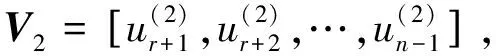
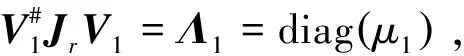
I

⊕也是正交矩阵,满足==，

其中

=，=⊕-⊕，=，=diag(1,

ε

+2,

ε

+2

ε

+3,…,

ε

+2…

ε

-1)，

则

det(

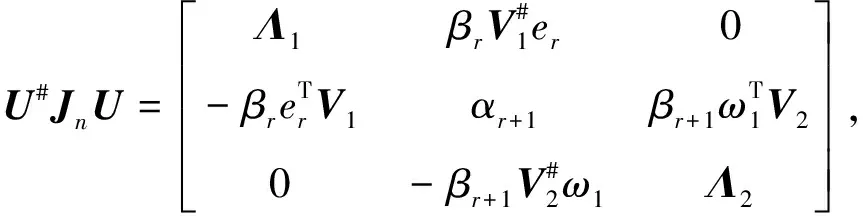
λ

-)=det(

λ

-)=

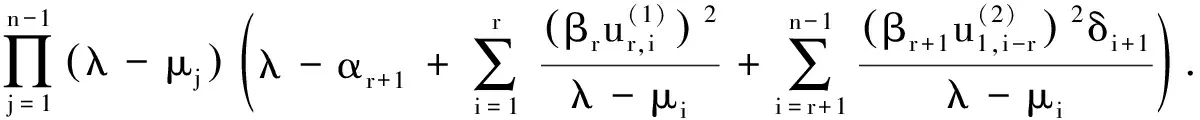
(4)

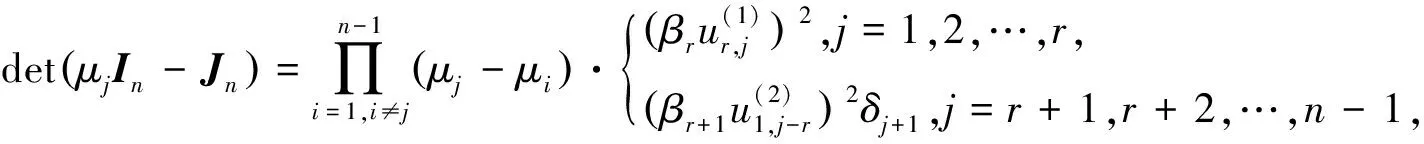
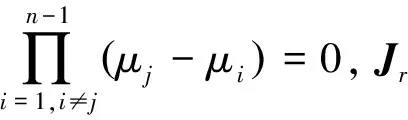
定理2

若

σ

()∩

σ

(+2,)=∅，则的特征值是函数

(5)

的

n

个零点.

证明

由于

σ

()∩

σ

(+2,)=∅，所以

μ

∉

σ

(),

j

=1,2,…,

n

-1

.

否则，如果

μ

∈

σ

()，则由定理1可知

μ

也为和+2,的公共特征值，这与条件矛盾.由(4)可知det(

λ

-)=0

等价于

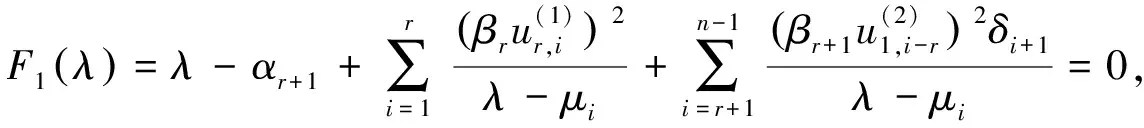
证毕.

的

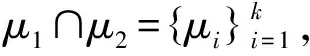
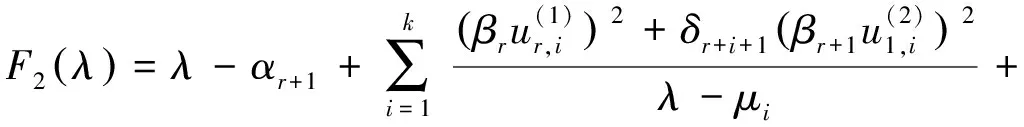
n

-

k

个零点.

证明

因为

μ

∈

σ

()∩

σ

(+2,),

i

=1,2,…,

k

，则

μ

,

μ

,…,

μ

是的特征值，因此由(4)可知，剩余的特征值是多项式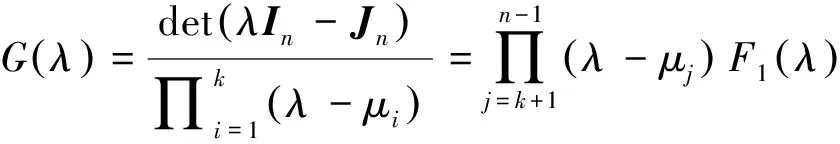

的零解.由于

μ

∉

σ

()∩

σ

(+2,),

i

∉{1,2,…,

k

}∪{

r

+1,

r

+2,…,

r

+

k

}，

时，

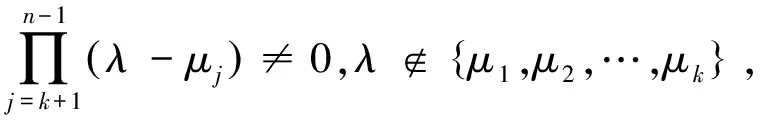
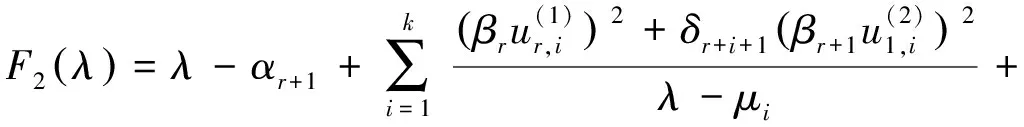
G

(

λ

)=0

.

此时

G

(

λ

)有

n

-

k

个零解，因此

F

(

λ

)也有

n

-

k

个零解.

引理2

已知{

ξ

,

ξ

,…,

ξ

,

η

,

η

,…,

η

-1}是由2

n

-1个成对且互不相同的复数构成的集合，则线性代数方程组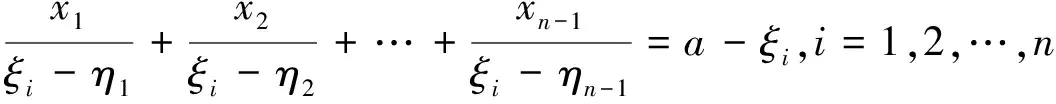

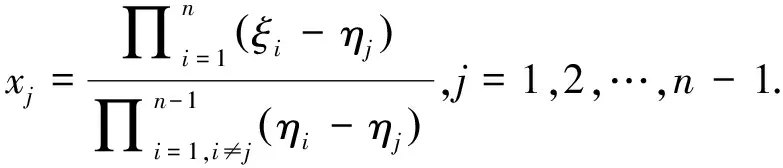
2 PJIEP有解的充要条件

对于如(3)所示的

λ

，

μ

和

μ

，按照

μ

∩

μ

=∅和

μ

∩

μ

≠∅两种情形讨论PJIEP的可解性.

定理4

对于如(3)所示的集合

λ

，

μ

和

μ

.

假设

μ

∩

μ

=∅，当且仅当满足下列条件时PJIEP有唯一解：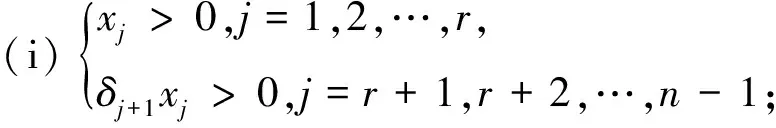

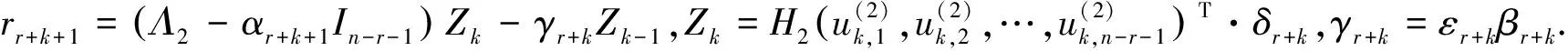
证明

必要性.假设存在一个形如(1)的伪Jacobi矩阵∈(

n

,

ε

,

β

)，

σ

()=

λ

，

σ

()=

μ

，

σ

(+2,)=

μ

，因为

μ

∩

μ

=∅，由定理2可知的特征值为(5)中

F

(

λ

)=0的解.由引理2可得

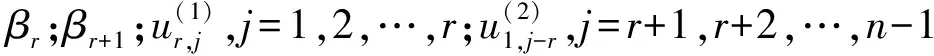
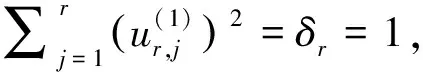
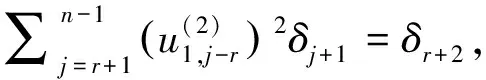
因此条件(ii)成立.又因为

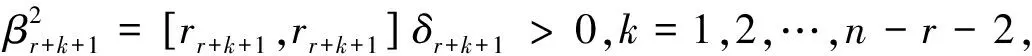
因此条件(iii)成立.

充分性.假设条件(i)～(iii)成立，此时考虑符号向量

ε

和非零实数

(6)

定义

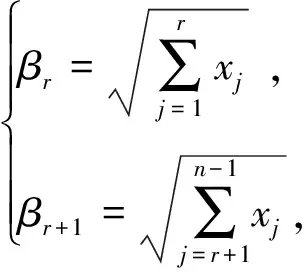
(7)

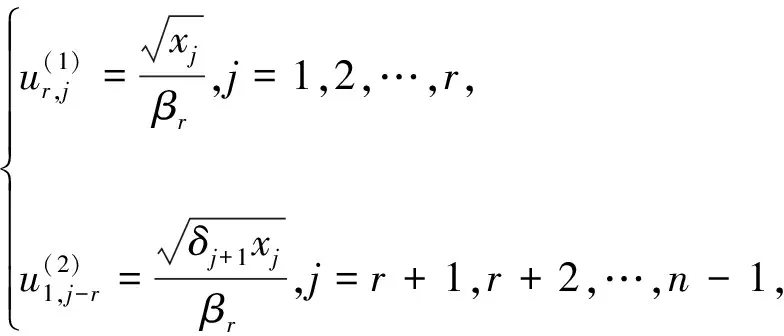
(8)

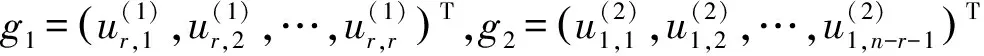
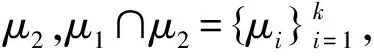
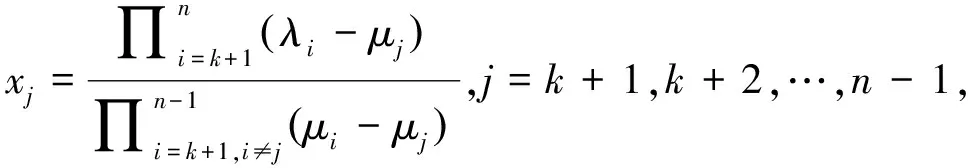
则当且仅当满足下列条件时PJIEP有解：

(i) 存在任意实数

θ

∉{0,1}，使得

θ

x

+>0,

δ

++1(1-

θ

)

x

+>0,

j

=1,2,…,

k

；

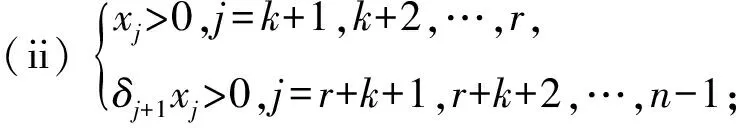
(iv) 定理4中的条件(iii)成立.

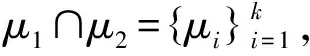
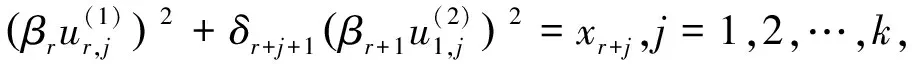
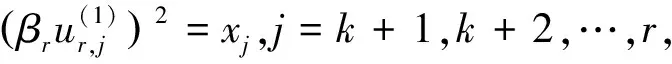
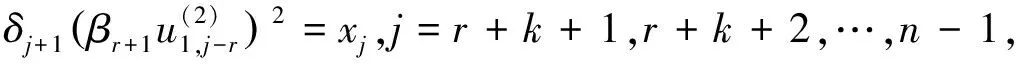
(9)

取任意实数

θ

∉{0,1}，使得

(10)

充分性.如果条件(i)～(iv)均成立，此时考虑符号向量

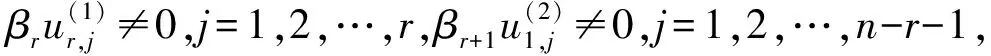
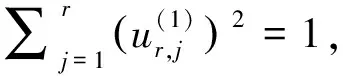
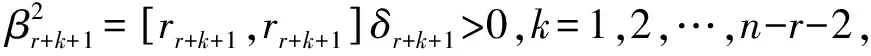
ε

和非零实数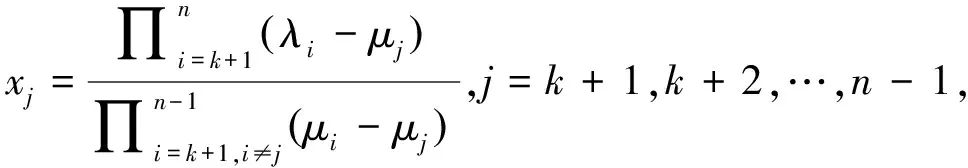

(11)

对于选定的

θ

∉{0,1},

j

=1,2,…,

k

，定义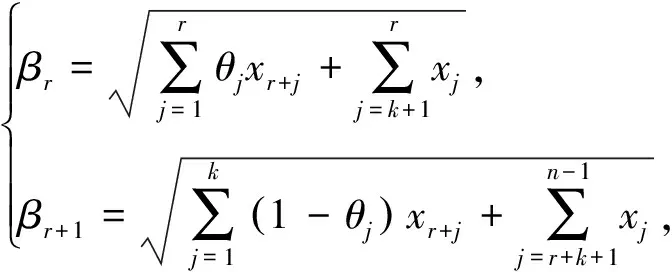

(12)

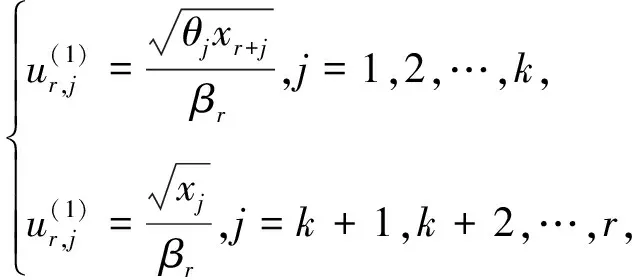
(13)

(14)

最后，验证已构造的伪Jacobi矩阵就是PJIEP的解.由公式(11)～(14)可知

对于任意的

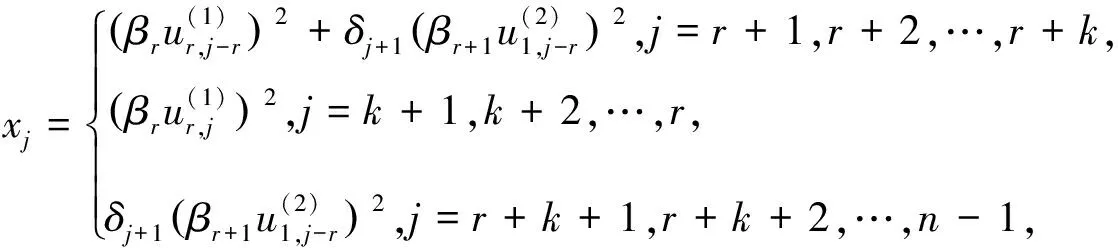
j

=1,2,…,

k

，取

由引理2可知

对所有的

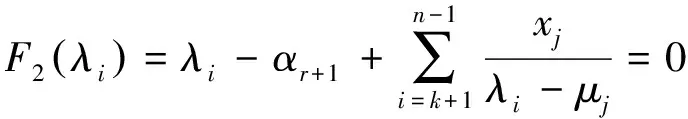
j

=

k

+1,

k

+2,…,

n

成立，于是由定理3可得det(

λ

-)=0,

i

=

k

+1,

k

+2,…,

n

，且

λ

+1,

λ

+2,…,

λ

是的特征值，又已知

λ

=

μ

∈

μ

∩

μ

,

i

=1,2,…,

k

是的其余特征值，因此

λ

=

σ

()，即是PJIEP的解.

3 数值算法

根据定理4,5，建立如下算法来构造集合(

n

,

ε

,

β

)中的伪Jacobi矩阵

.

算法 PJIEP的解

输入：如PJIEP中所示的

ε

,

λ

,

μ

,

μ

.输出:

J

(

n

，

ε

,

β

)

.

以下为各步骤：

1. 若

μ

∩

μ

=∅成立，接步骤2，否则接步骤6；

3. 如果满足定理4中的条件(1)～(2)，接步骤4，否则该问题无解；

4. 由(7)计算

β

和

β

+1；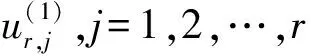

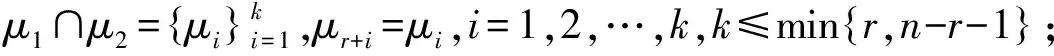
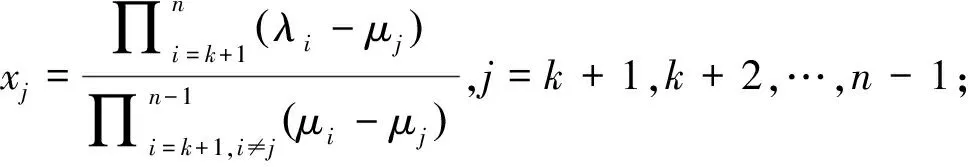
8. 如果满足定理5中的条件(1)～(3)，接步骤9，否则该问题无解；

10. 由(12)计算

β

和

β

+1；

15. 输出

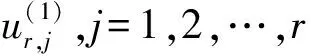
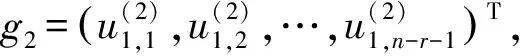
J

(

n

,

ε

,

β

)，结束.

4 数值实例

例子

令

n

=9,

r

=4，给定向量

ε

=(1,1,1,1,1,1,-1,1)和伪Jacobi矩阵∈

J

(9,

ε

,

β

)

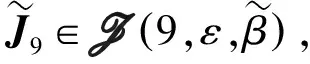
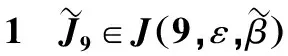
表的主对角元与下次对角元

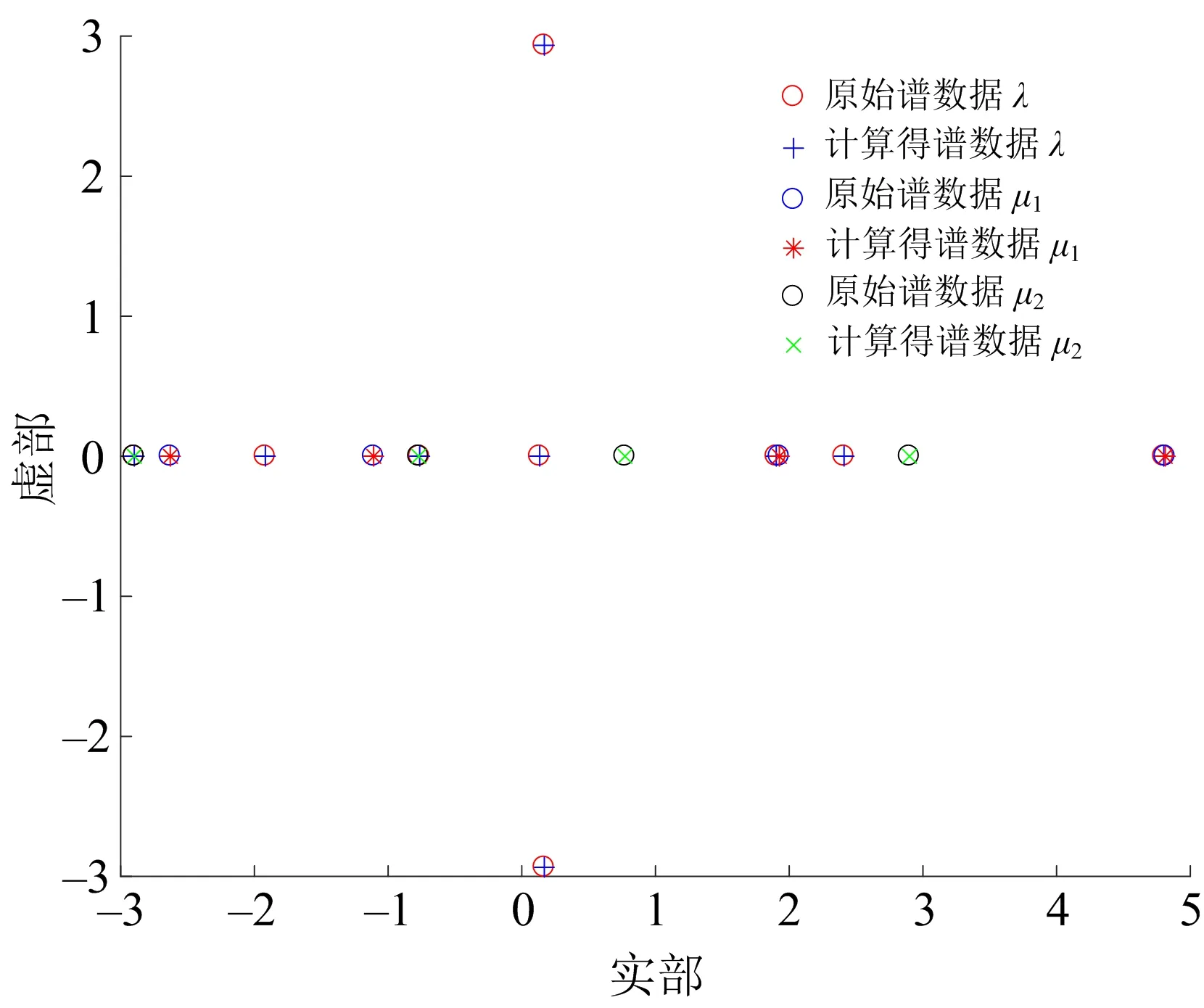
图1 原始谱数据λ,μ1,μ2和计算得到的谱数据的对比结果