基于混合算法的机器人路径规划

彭求志，田 丽，吴道华，李仕成

(安徽工程大学 高端装备先进感知与智能控制教育部重点实验室，安徽 芜湖 241000)

路径规划是在有障碍物的环境中按照评价标准(如最短路径、最低能耗、最低工时等)，在起点与目标点间寻找一条可行的无碰撞最优路径的策略.路径规划能保证机器人高效、安全、自主完成任务，在机械手臂、移动机器人等方面有广泛应用.根据机器人对工作区域信息的理解程度，路径规划可分为局部路径规划和全局路径规划.局部路径规划是机器人根据自身传感器实时采集的当前位置和局部障碍物信息，获取起点至目标点最优路径的策略，具有较高的实用性和实时性.局部路径规划的常见算法有：人工免疫算法、A算法、模糊算法及APF(artificial potential field method)等.全局路径规划是根据已知的全局环境和障碍物信息，利用寻优算法获取全局最优路径的策略.全局路径规划常见算法有：蜂群算法、遗传算法及RRT(rapidly-exploring random trees)算法等.RRT算法是一种增量式随机采样全局路径规划算法，占内存空间小，搜索能力强，在任何复杂环境下均能找到一条从起点到终点的路径，但此路径通常并不是最优路径.2011年，Karaman等对RRT算法进行了改进，提出了RRT(rapidly-exploring random trees star)算法.RRT算法能在搜索树扩展阶段为新节点选择代价最小的父节点，能找到渐进最优解且概率接近1，但由于迭代次数多、搜索时间长，使搜索效率及收敛速度均较低.2014年，Jonathan等提出了IRRT(informed rapidly-exploring random trees star)算法，在保证RRT算法的概率完备性及渐进最优性的基础上，引入椭圆偏置采样的方法，提高了搜索效率和收敛速度.笔者拟在IRRT算法的基础上，引入人工势场法的虚拟力场，提出APF-IRRT混合算法.

1 IRRT*算法

1.1 问题描述

轨迹函数表示与终点间的最佳轨迹，其表达式为

π

[,]=argmin{

π

|[0]=∧[

τ

]=}，

(1)

其中：为机器人某时刻的位置矢量.成本函数表示和终点间的搜索能耗，其表达式为

c

[,]=min{

π

|[0]=∧[

τ

]=}

c

[

π

]，

(2)

其中：

c

[

π

]为某段轨迹的成本.当0<

t

<

τ

时，有

π

[,]=

π

[,[

t

]]+

π

[[

t

],]，这表明最佳无碰撞轨迹可由

C

中一系列不连续状态(,,,…,)间的最佳轨迹连接而成.

1.2 椭球子集分析

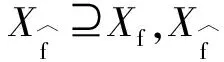
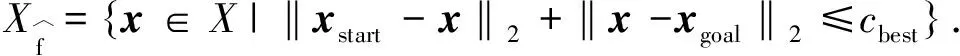
(3)

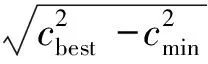
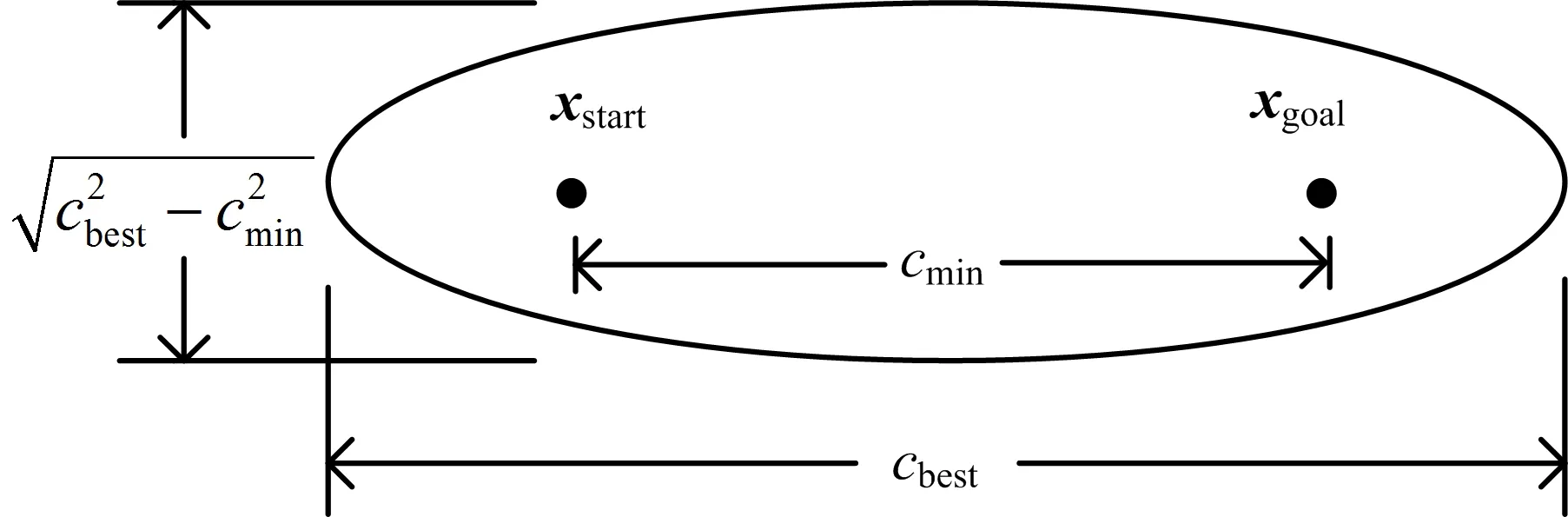
图1 椭圆偏置采样区域

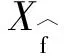
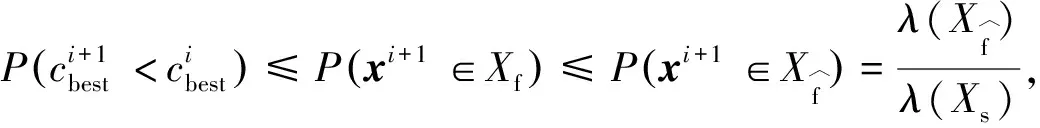
(4)

其中：

X

为包围已知子集的超长方体,

λ

(·)为度量比率.若采样区域是

n

维空间超球体，则解的最优性概率为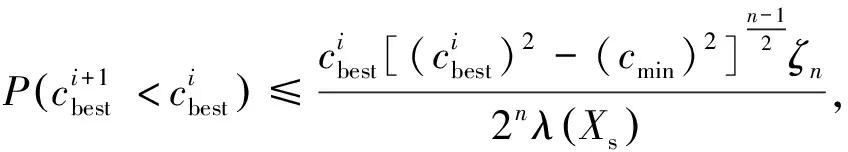

(5)

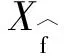
1.3 IRRT*算法描述

IRRT算法在保证算法的概率完备性以及渐进最优性的同时，能通过椭圆偏置采样提高算法收敛速度及效率.

IRRT算法的描述为：

1

V

←{}2

X

←

Φ

3

E

←

Φ

4

T

=(

V

,

E

)5 for iteration=1 to

n

do6

c

←min∈{Cost(

X

)}7←Sample(,,

c

)8←Nearnest(

T

,)9←Steer(,,StepSize)10 if CollisionFree(,) then11

X

←Nearest(

T

,,

r

RRT)12←Parent()13 if InEllipseRegion() then14

X

←

X

∪{}15 T.add Node()16 Return

T

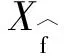
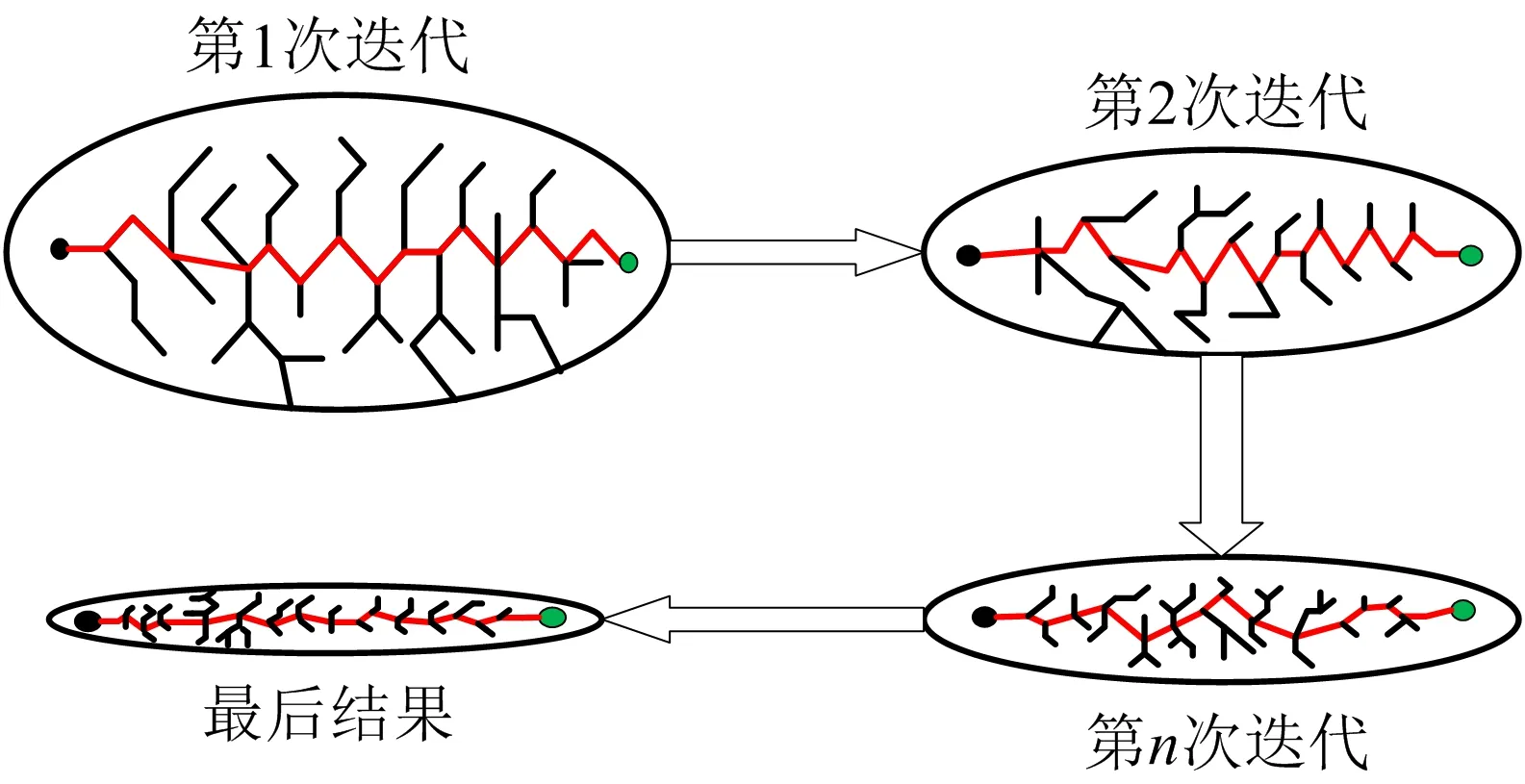
图2 IRRT*算法的迭代收敛过程

2 APF-IRRT*混合算法

IRRT算法虽提高了RRT的收敛速度，但扩展节点的获得是完全随机的，整个搜索过程无导向性、无启发性.针对IRRT算法的不足，笔者将APF和IRRT算法相结合，提出APF-IRRT混合算法.

2.1 混合算法的流程及步骤

APF-IRRT算法把人工势场法的虚拟力场加至I-RRT算法，通过父节点的改写保证IRRT算法的完备性及最优性，通过延迟椭圆偏置采样及后置碰撞检测，减少算法的计算量，加快算法收敛速度.混合算法流程如图3所示.

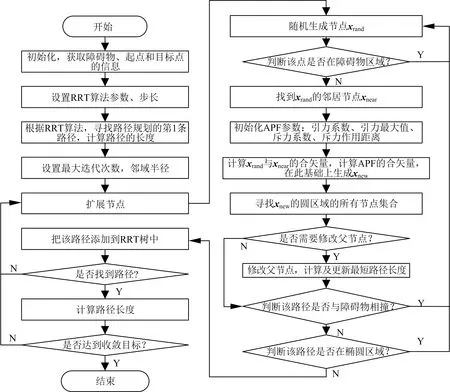
图3 混合算法流程图

混合算法的具体步骤如下：

步骤 1 获取障碍物的信息，确定规划路径起点的位置矢量和目标点的位置矢量.

步骤 2 设置循环迭代次数、邻域半径、算法步长.

步骤 3 采用RRT算法规划第1条路径，并计算路径长度

c

及起点到目标点的距离

c

.步骤 4 随机产生节点位置矢量，寻找邻居节点的位置矢量，计算与的合矢量.步骤 5 初始化APF参数，计算APF的合矢量.步骤 6 计算与的合矢量，根据及步长计算新的位置矢量，改写父节点.

步骤 7 对路径进行碰撞检测及椭圆区域检测.

步骤 8 是否找到起点到目标点的路径？如果是，就计算路径长度；如果否，就扩展随机树.

步骤9 是否达到收敛目标？如果否，就扩展RRT树的节点，直至收敛；如果是，算法结束.

2.2 混合算法描述

混合算法的描述为：

1

V

←{}2

X

←

Φ

3

E

←

Φ

4

T

=(

V

,

E

)5 for iteration=1 to

n

do6

c

←min∈{Cost(

X

)}7←Sample(,,

c

)8←Nearnest(

T

,)9←Steer(,,,map,stepsize)10 if CollisionFree(,)then11

X

←Nearest(

T

,,

r

RRT)12←Parent()13 if InEllipseRegion()then14

X

←

X

∪{}15 T.add Node()16 Return

T

混合算法将人工势场法的虚拟力场添加至IRRT算法,产生了新的节点(见混合算法描述的第9行)，提高了搜索效率.混合算法关键的Steer环节通过以下3步操作实现.第1步，计算与的合矢量(图4(a))；第2步，通过APF计算和，再计算合矢量(图4(b))；第3步，计算与的合矢量(图4(c)).

图4 Steer环节的3步操作示意图

Steer环节的算法描述如下：

1 if∈

C

then2←atan2(,)3 angle←angle(,,map,length(map))4 Calculation()5←APF_attact(,,angle,AFP_a,AFP_amax)6←APF_attact(,,angle,AFP_a,AFP_amax)7←atan2(,)8←Steer(,,stepsize)

9 else

10～

U

(

X

)11 Return

T

3 仿真实验

3.1 不同算法的仿真结果

仿真区域为250 m×150 m.APF的设置如下：APF_a=0.01,APF_amax=1,APF_r=0.5,APF_po=50.RRT算法的设置如下：最大迭代次数为3 000，与的步长均为7.4种算法的仿真结果如图5所示.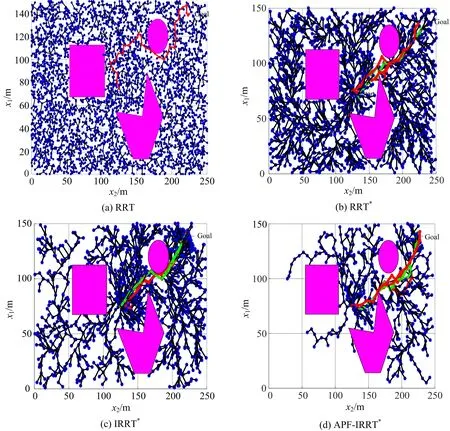

图5 4种算法的仿真结果

由图5(a)可知，RRT算法采用遍历式扩展，地图中扩展的节点很多，但是很多节点是无效节点.由图5(b)可知，RRT算法保证了算法的完整性和最优性，但扩展节点仍然较多.由图5(c)可知，IRRT算法在椭圆约束下，减少了扩展节点的数目，但很多扩展节点在无效区域.由图5(d)可知，APF-IRRT算法减少了无效区域扩展节点的数目.

使用4种算法对同一地图进行20次实验，表1为20次实验数据的平均值.由表1可知，相对于其他3种算法，APF-IRRT算法搜索时间、节点数目、路径长度的数值均最小.根据算法的搜索时间，可算得APF-IRRT算法的效率相对于IRRT提高了约35%.

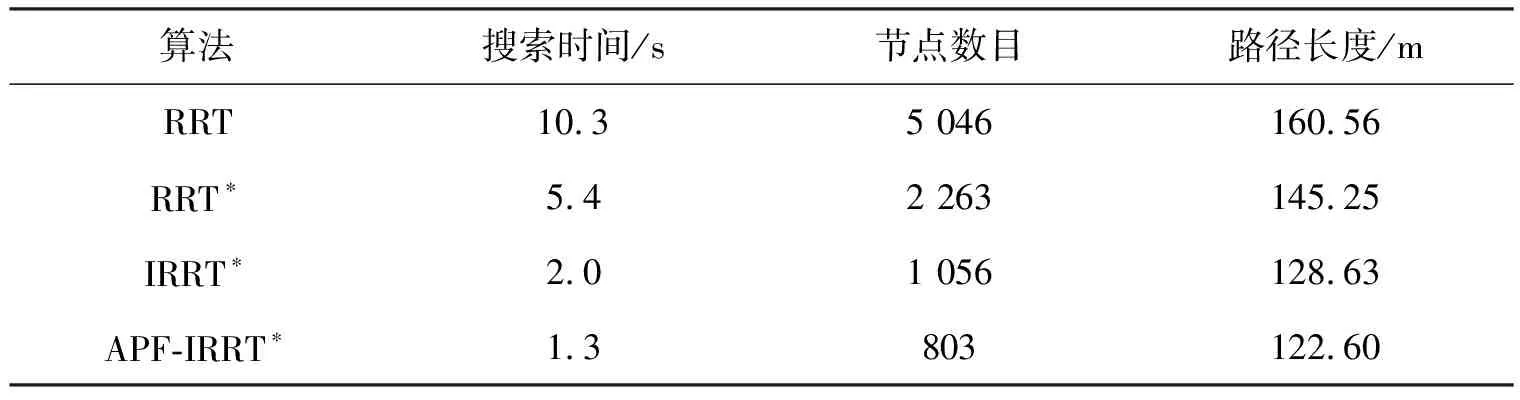
表1 4种算法20次实验数据的平均值

3.2 地图复杂度及面积对算法搜索时间的影响

使用4种算法对两种复杂度以及两种面积的地图进行实验，20次实验的搜索时间平均值如图6所示.由图6可看出，地图的复杂度及面积没有改变曲线的趋势，也没有改变APF-IRRT算法相对于其他3种算法的优越性.可见，APF-IRRT算法对地图的复杂性及面积的变化均有较强的适应能力.

图6 地图复杂度及面积对算法搜索时间平均值的影响

4 结束语

笔者将人工势场法的虚拟力场与IRRT算法相结合，提出了APF-IRRT混合算法.通过仿真实验验证该算法的可行性，4种算法的实验结果表明：相对于RRT，RRT，IRRT算法，APF-IRRT算法搜索时间、节点数目、路径长度的数值均最小,对地图的复杂性以及面积的变化均有较强的适应能力.