一类不确定分数阶舰船运动混沌系统的滑模同步控制
2021-09-11 03:28程春蕊毛北行
安徽大学学报（自然科学版） 2021年5期
程春蕊，毛北行
(郑州航空工业管理学院 数学学院，河南 郑州 450015)
混沌系统具有不可预测性,是一类非常复杂的非线性动力学系统，对初始条件和系统参数变化都异常敏感.混沌系统的同步问题引起了许多研究者的关注，并在很多领域得到了广泛应用.到目前为止，各种控制技术已经成功地应用于混沌系统的同步.随着分数阶微积分的发展，人们已经认识到，许多跨学科领域的系统可以用分数阶微分方程精确描述.分数阶混沌系统的同步控制方法也被相继提出.文献[12]研究两个不确定分数阶混沌系统的同步问题,设计了一种强鲁棒性的分数阶滑模面和自适应滑模控制器,实现两个混沌系统的同步.文献[13]运用分数阶微积分的稳定性理论,通过设计适当的控制器,实现不同节点复杂网络的混合投影同步.滑模控制因其实现简单、响应快、对外界干扰敏感性低等优点引起人们越来越多的关注.文献[14]基于自适应控制研究方法,研究含有随机扰动和未知参数的分数阶Rayleigh-Duffing-like系统的同步问题，通过设计合适的控制器和参数的辨识规则,实现系统的广义投影同步.文献[15]给出一种有效的船舶混沌运动自适应控制方法.文献[16]结合自适应控制和滑模控制方法，研究舰船混沌运动的单输入自适应变结构控制问题.而有关分数阶的舰船混沌运动的同步方面的结果还不多见.论文研究一类不确定分数阶舰船运动混沌系统的滑模同步控制问题，基于Lyapunov稳定性理论给出系统取得同步的充分性条件，结果表明选取适当的控制律以及自适应控制律下，舰船误差系统取得了滑模同步.
1 主要结果
研究如下一类舰船转首操纵运动混沌模型
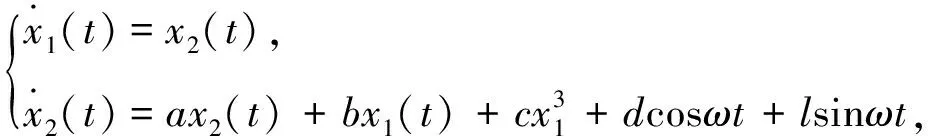
(1)
定义1
函数x
(t
)的α
阶Caputo分数阶导数定义为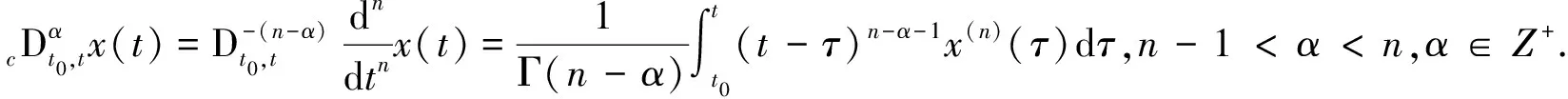
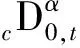
考虑分数阶舰船运动混沌系统
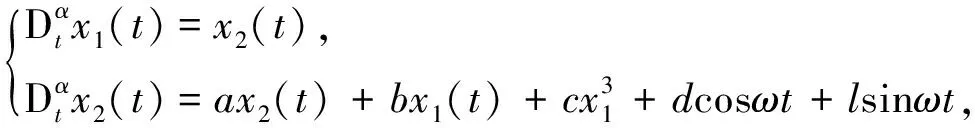
(2)
当系统参数a
=-0.
320 8,b
=0.
271 5,c
=-4.
394 5,d
=0.
103 68,l
=0.
077 8,ω
=0.
8,α
=0.
93时，系统呈现混沌态. 以上述系统作为驱动系统，设计响应系统为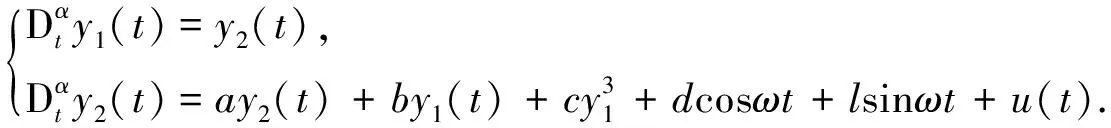
(3)
定义同步误差e
=y
-x
,e
=y
-x
,则误差系统为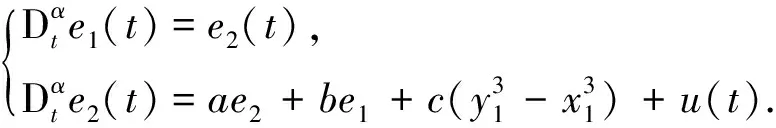
(4)
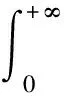
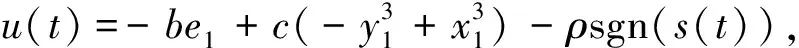
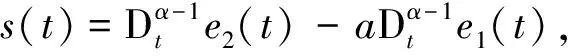
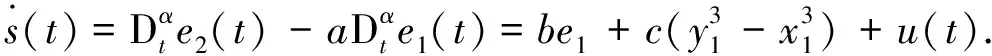
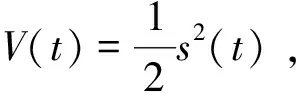
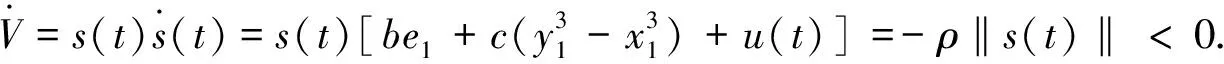
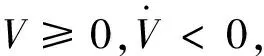
由于海上航行处于复杂的环境中，受到多种不确定因素的影响，又因为分数阶系统能更准确地描述实际系统，因此在上述系统的基础上，考虑如下不确定舰船混沌运动
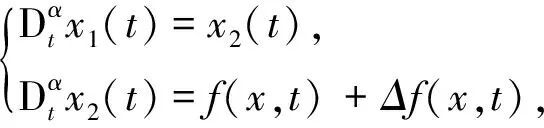
(5)
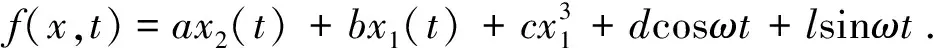
以上述系统作为驱动系统，设计响应系统为
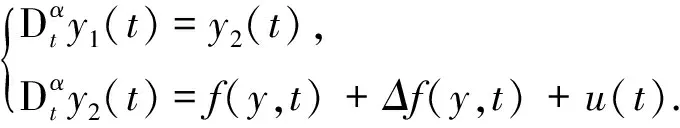
(6)
定义同步误差e
=y
-x
,e
=y
-x
,则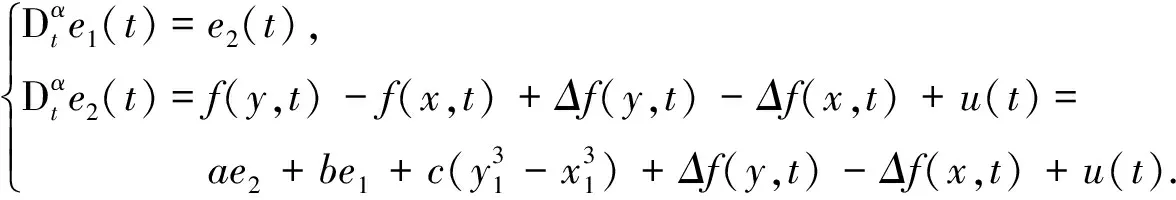
(7)
假设1
‖Δf
(y
,t
)-Δf
(x
,t
)‖≤ρ
<+∞.
定理2
设计控制器为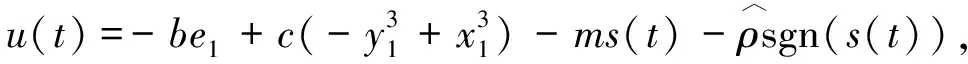
设计滑模面
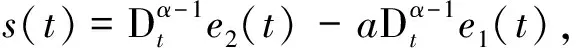
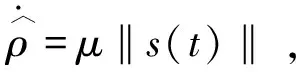
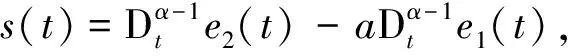
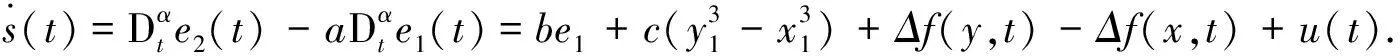
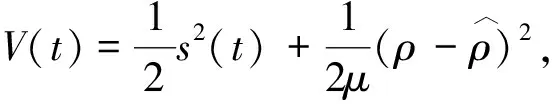
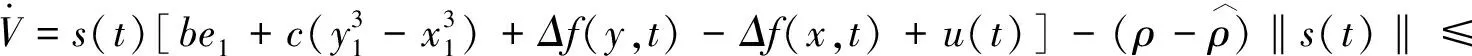
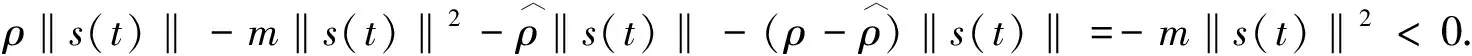
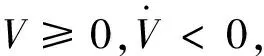
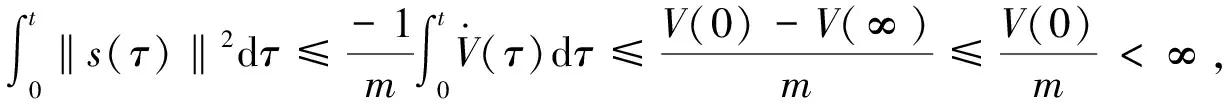
s
(t
)是平方可积的，根据引理1可知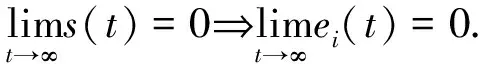
2 数值仿真
定理1中，当系统参数a
=-0.
320 8,b
=0.
271 5,c
=-4.
394 5,d
=0.
103 68,l
=0.
077 8,ω
=0.
8,α
=0.
93时，系统呈现混沌态. 用MATLAB进行数值仿真，采取4阶Rung-Kutta方法,仿真步长取为0.01 s,系统初始值设置为(x
(0),x
(0))=(0,0)，(y
(0),y
(0))=(-1.
75,-0.
75)，(e
(0),e
(0))=(-1.
75,-0.
75),设定舰船初始航向为(0,45°)，其系统误差曲线如图1所示.从图1可以看出，系统开始时刻，两变量的误差曲线距平衡点较远，随着时间的推移，系统误差曲线渐趋平衡点.定理2中用MATLAB进行数值仿真，采取4阶Rung-Kutta方法, 系统参数a
=-0.
320 8,b
=0.
271 5,c
=-4.
394 5,d
=0.
103 68,l
=0.
077 8,ω
=0.
8,α
=0.
93，初始值(x
(0),x
(0))=(0,0),(y
(0),y
(0))=(-2.
25,-1.
25),(e
(0),e
(0))=(-2.
25,-1.
25),不确定项Δf
(x
,t
)=
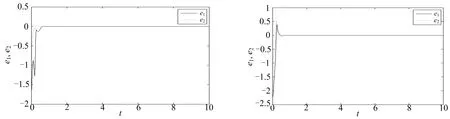
图1 定理1中的系统误差曲线 图2 定理2中的系统误差曲线
3 结束语
基于Lyapunov稳定性理论研究一类不确定分数阶舰船运动混沌系统的滑模同步控制问题，研究表明，一定条件下舰船误差系统能够取得滑模混沌同步.如何将系统的外部扰动也考虑在内是需要进一步研究的课题.
