Fisher矩阵与Fisher张量
徐常青,冯 岩,宋 珊
(苏州科技大学 数学科学学院, 江苏 苏州 215009)
Fisher信息矩阵 (Fisher information matrix,简称FIM), 即Fisher矩阵, 起源于20世纪30年代, 它在统计、建模等领域中扮演着关键角色. FIM还被广泛运用于心理学、相对论和宇宙学关于黑洞(Black hole)的预测等方面. FIM在统计学中主要用于实验设计或预测模型参数对实验数据的依赖程度. 只要知道模型和测量不确定度, 就可建立FIM. 在贝叶斯统计中, 根据Bernstein-von Mises定理, 后验模式渐近分布取决于Fisher信息而非取决于先验信息. Ronald Fisher强调了FIM在最大似然估计的渐近理论中的作用, Francis Y. Edgeworth在此方面的工作见文献[5].Fisher矩阵对应于最大似然估计渐近分布协方差矩阵的逆矩阵, 因此标准化假设下Fisher矩阵可用于估计一个概率分布的协方差矩阵.为解决不完整数据的最大似然估计, Louis提出一种应用EM(expectation-maximum) 算法时通过样本观测值计算Fisher矩阵的方法, 由此得到的Fisher矩阵可用于构造渐近置信区间.Fisher矩阵还可被用于统计数据检验, 如Wald检验等.
1 预备知识

τ
∈S
(0;m
,n
)⟺τ
=(1,1,…,1),且τ
∈S
(N
;m
,n
)⟺τ
=(n
,n
,…,n
),即τ
是集合S
(m
,n
)中最大的元.的元,,…,也用表示, 其中σ
=(i
,i
,…,i
).
对张量=()∈T
,, 若每个元,,…,在下标的任意置换下其值不变, 即=(),∀τ
∈Sym
,∀σ
∈S
(m
,n
)( 集合[m
]上所有置换的集合), 则称为对称张量.用ST
;表示所有m
阶n
维对称张量的集合.
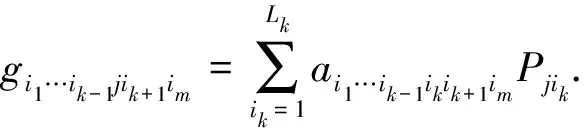
(1)
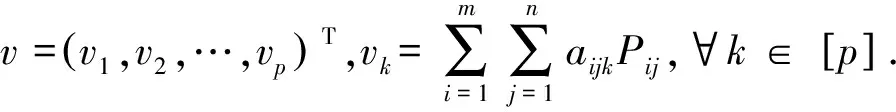


考虑对数似然比
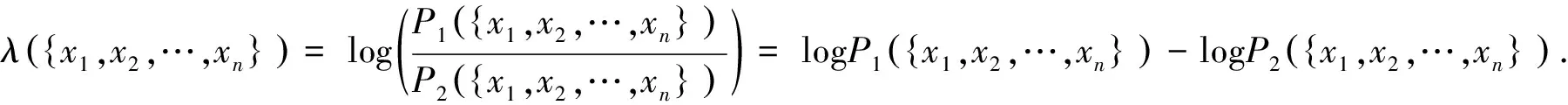

λ
({x
,x
,…,x
})|>δ
,(2)
则称(P
,P
)具δ
-区分度, 使(P
,P
)具δ
-区分度的样本集X
称为δ
-可区分样本集, 最小δ
-可区分样本集X
所含样本点个数N
称为(P
,P
)可δ
-区分最小统计量. 进一步, 若λ
>δ
,视样本集X
服从P
分布, 若λ
<-δ
<0, 则视X
服从P
分布.若λ
不满足式(2), 即|λ
({x
,x
,…,x
})|≤δ
,则认为P
,P
都有效, 称(P
,P
)不具δ
-区分度. 假设所有样本点均服从P
分布, 那么λ
(x
)的期望为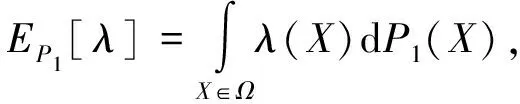
(3)
其中:Ω
为样本空间. 在样本空间为离散空间的前提下, (3)式定义的Kullback-Liebler散度D
为
D
不一定满足对称性, 即等式D
(P
‖P
)=D
(P
‖P
)(4)
不一定成立, 故D
并非真正意义下的距离度量.然而若P
,P
“充分接近”, 则D
可近似满足式(4).为此, 可以定义两个概率分布P
,P
的概率样本距离为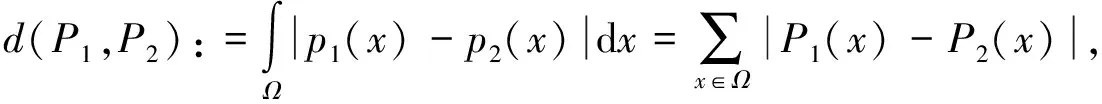
ε
>0,P
的ε
-邻域B
(P
,ε
)定义为B
(P
,ε
):={P
(x
):d
(P
,P
)<ε
}.
对一个给定的足够小的ε
>0, 有引理1.
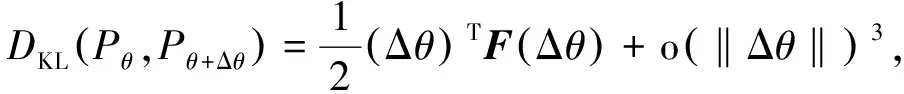
θ
‖为Δθ
的2-范数,是Fisher信息矩阵, 其元素用下式表示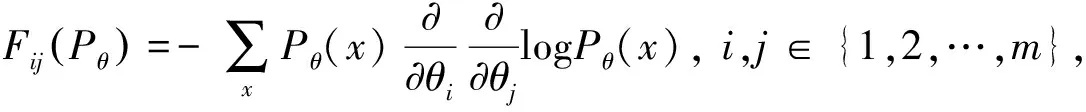
由此可见,Fisher信息矩阵可用于概率分布函数空间的度量.
2 Fisher信息量和Fisher矩阵的定义与性质
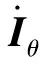

(5)
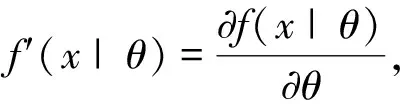
定义2
包含在随机变量X
中的Fisher信息量(对于θ
)定义为
(6)
引理2
设随机变量X
的密度函数f
=f
(x
|θ
)及其偏导∂f/
∂θ
为连续函数,其中θ
为参变量. 则X
的Fisher信息量(θ
)满足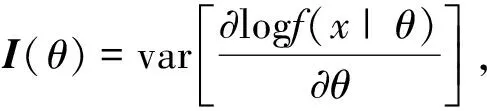
和
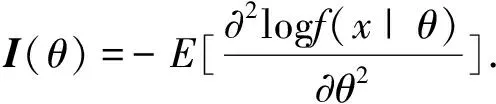


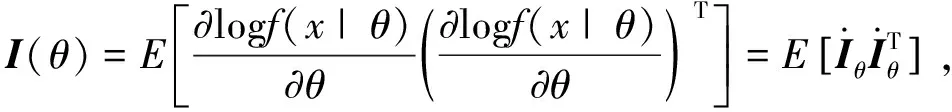
(7)
其中
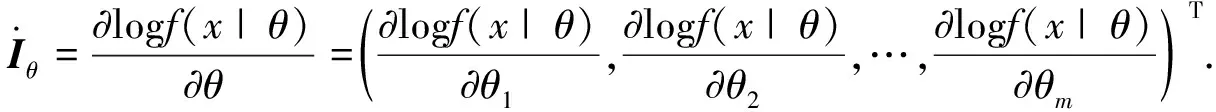

θ
)为对称正定矩阵;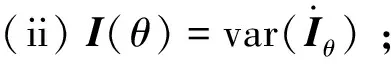
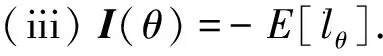
证明
(1) 记(θ
)=(), 则对任意下标[m
]×[m
], 由式(7)可得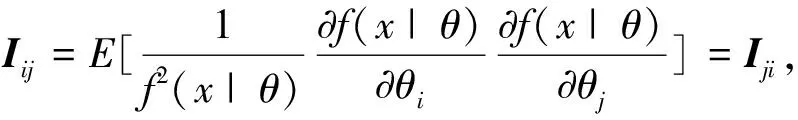
θ
)为对称矩阵. 接下来证明(θ
)为正定矩阵.对任意的不全为零随机向量x
, 有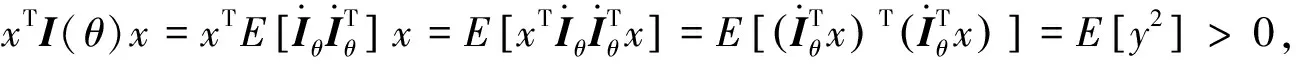
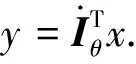
(ii) 注意到
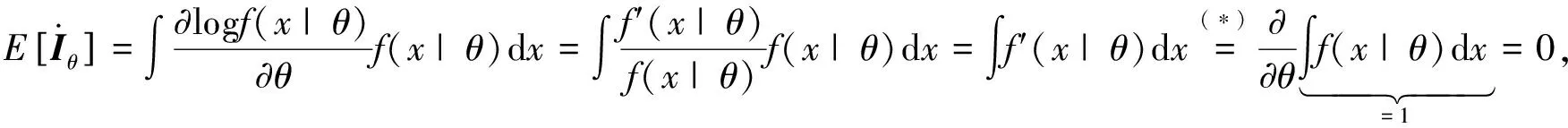
因此
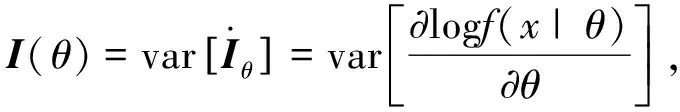
故(ii)成立.
(iii) 由引理1可得.
性质2
单调性.设T
=T
(x
)是X
的一个统计量,X
和T
对应的信息量分别为(θ
)和(θ
), 则(θ
)≤(θ
),当且仅当T
=T
(x
)是X
的一个充分统计量时等号成立.性质3
若随机变量X
,X
,…,X
为独立变量, 则随机向量X
=(X
,X
,…,X
)关于模型参数θ
的Fisher信息满足可加性, 即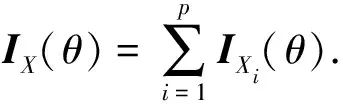
(8)
证明
设X
对应的密度函数为f
(x
|θ
), 则其联合密度函数为
因此
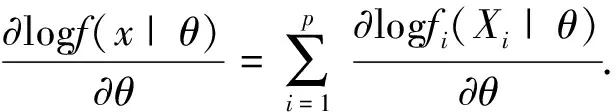
(9)
由性质1中的(ii), 结合式(9)和随机变量X
,X
,…,X
的独立性, 有
因此式(8)得证.
推论1
设X
=(X
,X
,…,X
)为随机向量, 其中X
,X
,…,X
独立同分布, 设X
的Fisher信息满足(θ
)=(θ
), 则随机向量X
的Fisher信息为(θ
)=p
(θ
).
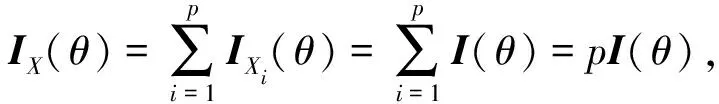
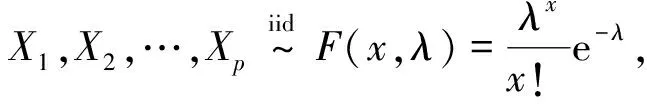
例2
若X
=(X
,X
,…,X
)独立同分布于指数分布e-, 即其密度函数为p
(x
|θ
)=θ
e-,x
>0,θ
>0.
由式(7)可得(θ
)=1/θ
, 从而由推论1得X
的Fisher信息(λ
)=p
(λ
)=p/θ
.
下面的性质反映了参数变换下Fisher信息的变化.
性质4
设随机变量X
的密度函数为f
(x
|θ
),θ
=φ
(μ
), 且φ
是可微函数,(θ
),(μ
)分别表示X
关于参数θ
和μ
的Fisher信息,有(μ
)=[φ
′(μ
)][φ
(μ
)].
证明
令g
(x
|μ
)为X
的以μ
为参数的概率密度函数, 则logg
(x
|μ
)=logf
[x
|φ
(μ
)]=l
(x
|φ
(μ
)),从而
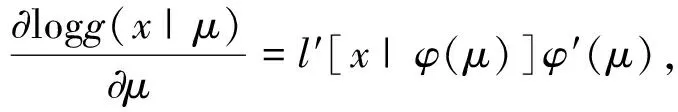
因此

性质5
设(θ
)是随机向量X
关于模型参数θ
的Fisher信息,f
是随机向量X
的可测函数, 且概率密度为φ
(f
|θ
), 则f
关于模型参数θ
的Fisher信息为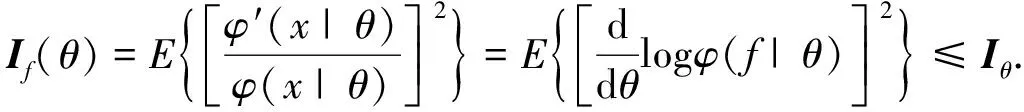

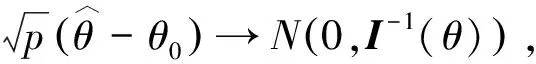
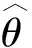
X
,…,X
的参向量θ
的最大似然估计(maximum likelihood estimation,简称MLE)渐近分布(正态分布)的协方差矩阵为其Fisher矩阵的逆, 这里要求随机变量X
,…,X
为独立同分布.

3 协方差张量和Fisher张量


a
…)∈T
,和=(b
…)∈T
,时, 它们的张量外积为∘=(a
…b
+1…+)∈T
+,,

X
,X
)=E
[(X
-E
[X
])∘(X
-E
[X
])],
x
)=E
[(X
-E
[X
])∘(X
-E
[X
])]=m
(x
).

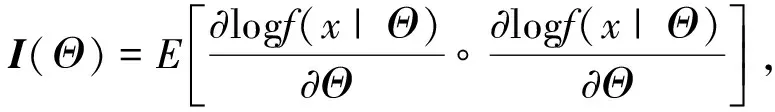
(10)

Fisher信息张量有很多好的性质, 如对称性和正定性, 它不仅与充分统计量有内在联系, 而且还可以进行参数转换, 得到不同参数化的Fisher张量.

Θ
)为对称正定张量;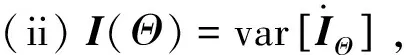
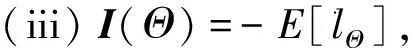
证明
(i) 记(Θ
)=(……), 则由式(7)可得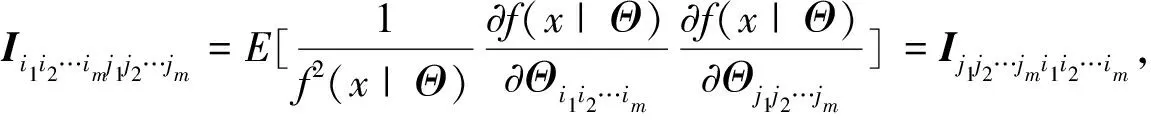
Θ
)为对称张量. 接下来证明(Θ
)为正定张量.对任意的不全为零随机张量x
, 有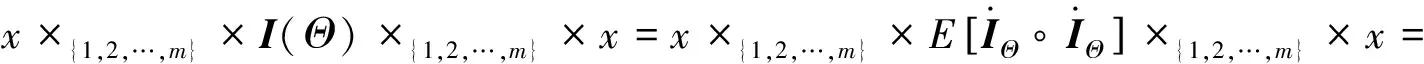

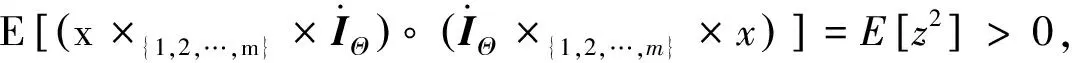
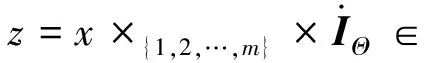
(ii) 注意到
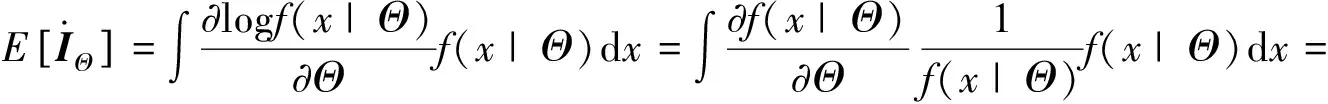
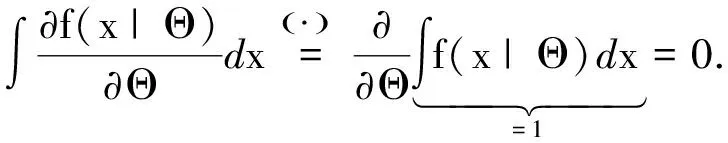
f
(x
|Θ
)的光滑性来保证. 因此, 由上式可以得到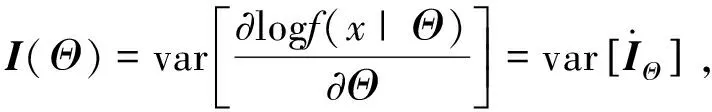
故(ii)成立.
(iii) 因为

(11)
所以由式(11)得到Fisher信息张量等于
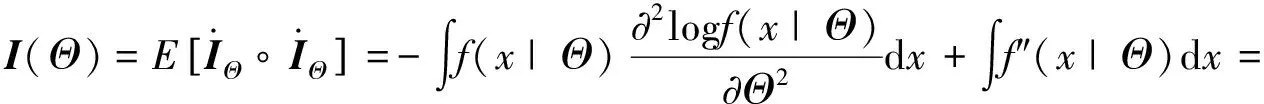
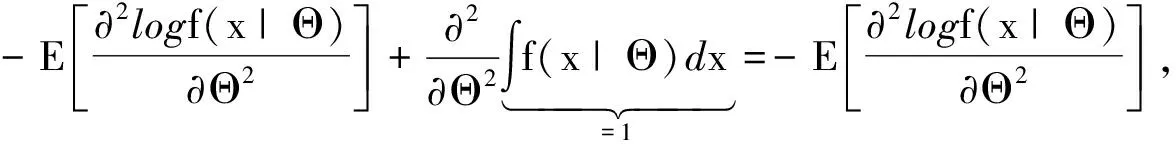
其中
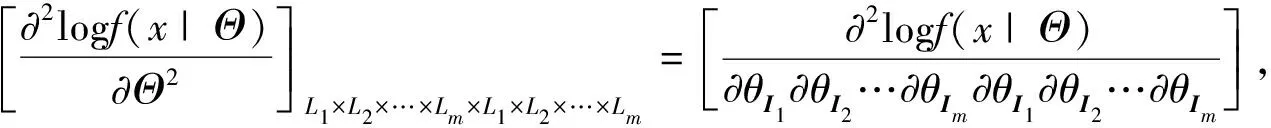
即
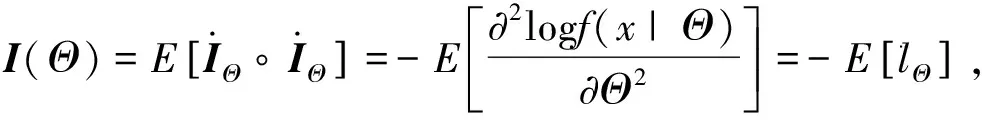
故(iii)成立.
由于一个随机张量可通过张量的纤维化等价地表示为一个随机向量, 结合性质2, 可得下面关于随机张量统计量函数的单调性结论.

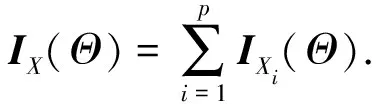
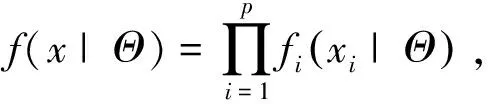

由于总和的随机张量是独立的,对上式左右两边同时求协方差张量
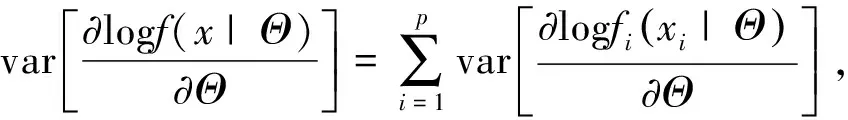
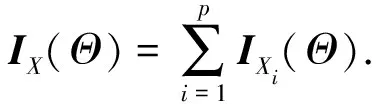
推论4
如果X
,X
,…,X
是独立同分布的,X
=(X
,X
,…,X
)为联合随机张量, 若对所有的X
,其Fisher张量满足(Θ
)=(Θ
), 有(Θ
)=p
(Θ
).
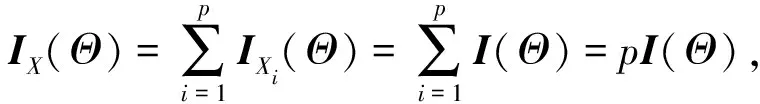
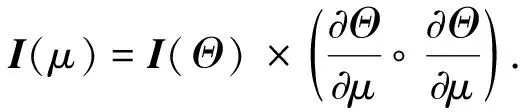
证明
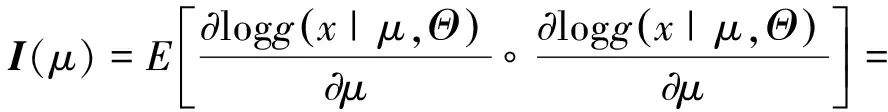
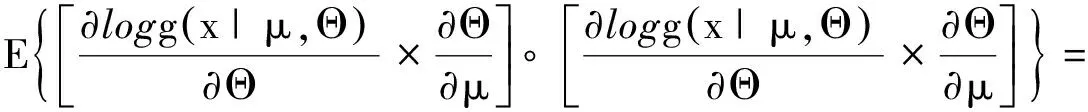
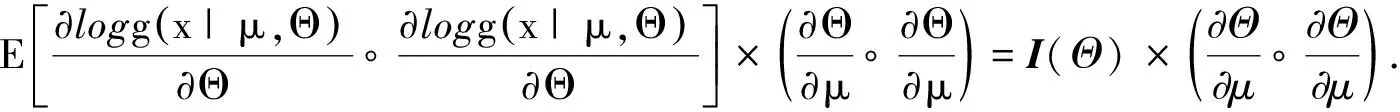
性质10
设(Θ
)是随机张量X
关于模型参数Θ
的Fisher张量, 概率密度为g
(x
|Θ
),是随机张量X
的可测函数, 且概率密度为h
(f
|Θ
), 则关于模型参数Θ
的Fisher张量为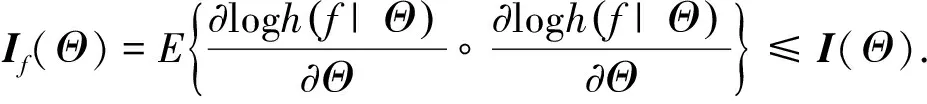
上式表明, 经过处理的数据信息量可能下降.在实际情况中, 为了降低噪声的干扰或为了方便数据分析, 可以对原始数据进行适当的处理.
证明
设随机张量X
的取值空间为X, 函数f
的取值空间为F
, 有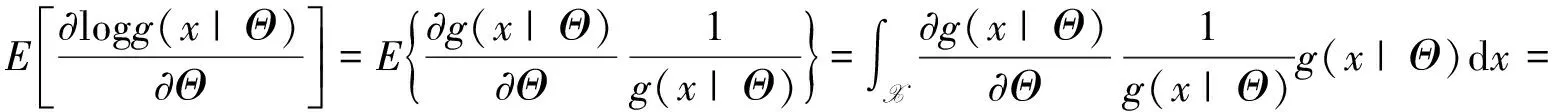

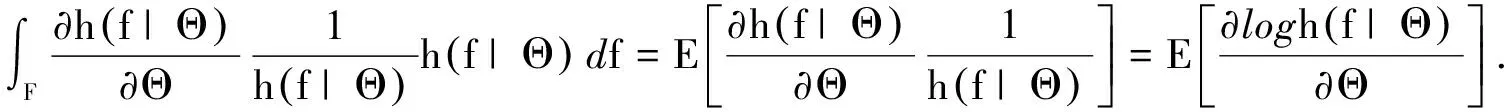
根据条件数学期望的概念, 有

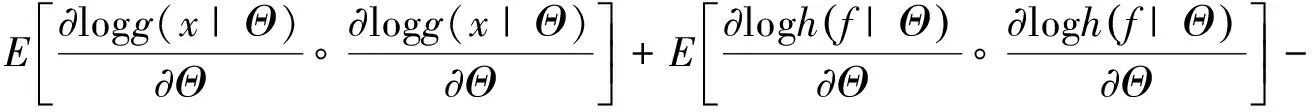
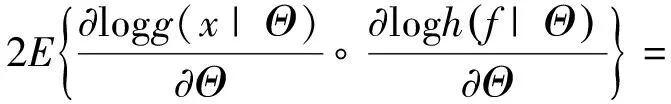
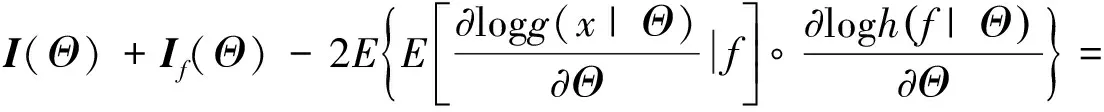
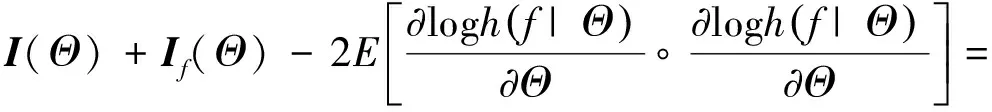
Θ
)+(Θ
)-2(Θ
)=(Θ
)-(Θ
)≥0.

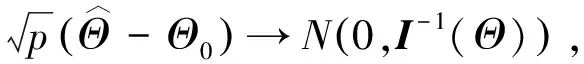
(12)
其中:(Θ
)是(Θ
)的逆.
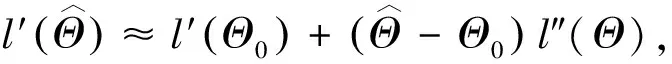

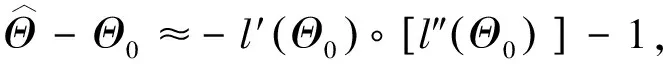
从而
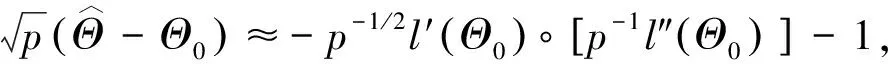
(13)
因为
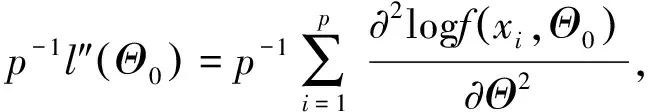
根据大数定律,得

(14)
结合(13),(14),得

(15)
从而
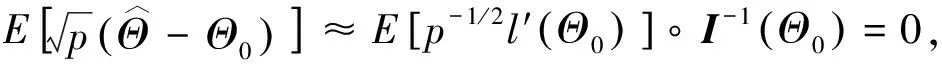
注意到
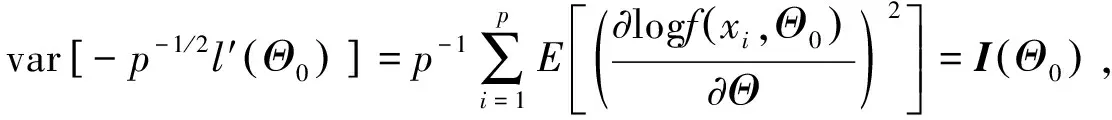
(16)
由(15),(16), 得
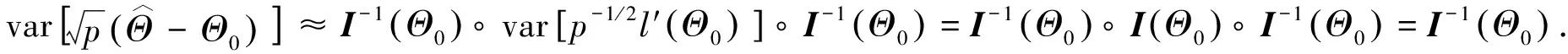
应用中心极限定理,得(12), 证毕.
4 结束语
论文主要介绍了Fisher信息和Fisher信息矩阵, 其导数或矩阵的逆是最大似然估计量的渐近分布的方差或协方差矩阵. 基于Fisher信息矩阵的对称性、非负性等性质, 引入协方差张量和Fisher信息张量, 得到参数最大似然估计量的渐近分布的协方差张量是Fisher张量的逆, 同时讨论了Fisher信息张量的性质.

