基于组合权重灰色关联-TOPSIS法的高模量沥青综合性能评价

李辉 王思淼

摘要：随着RK300高模量沥青的广泛使用，为了选择最合适的RK300改性剂掺量，建立了组合权重灰色关联-TOPSIS法的沥青混合料综合性能评价模型。在阅读相关文献的基础上，构建了沥青综合性能评价体系，首先采用层次分析法求出各项性能指标的主观权重，通过组合数有序加权算子（C-OWA）进行主观权重的修正，在借助熵权法进行客观赋权，将主、客观权重通过线性加权法进行组合，得到组合权重。将TOPSIS和灰色关联模型相结合，计算各掺量方案与正负理想解之间的相对贴近度并排序，选择最佳的方案，结论为掺量为0.30%的RK300高模量沥青混合料综合性能最佳。研究结果表明，本文建立的沥青综合性能评价模型科学合理，能够达到对不同RK300改性剂掺量方案进行优选的目的。

关键词：高模量沥青;综合评价;C-OWA;灰色关联理论

引言

近几十年来，我国的公路交通量增长迅猛，超载和重载现象频繁发生，对沥青路面产生了损害。为了解决这一问题，高模量沥青混合料应运而生，通过直接添加高模量改性剂到沥青集料中来改善沥青的路用性能，不同掺量的改性剂改善效果也不同，为了找到适合的掺量值，就需要建立沥青混合料综合性能的评价模型来量化不同掺量的高模量沥青混合料的综合性能。本文借鉴组合赋权的思想，首先利用层次分析法得到主观权重，借助有序加权算子（OWA）对主观权重进行修正，以降低主观偏好对权重的影响，之后利用熵权法得到客观权重，避免人为因素造成的误差，最后将主客观赋权方法结合，使最终计算出的权重更加可靠。关于评价方法的研究，本文在建立沥青混合料性能评价指标体系的基础上将TOPSIS法和灰色关联理论与结合，构建基于TOPSIS-灰色关联法的沥青混合料综合性能评价模型 。

1 高模量沥青混合料综合性能评价指标体系

本文参考文献[1]的实验数据，得到不同掺量RK300高模量沥青各指标的数据，见表1。其中评价指标一共有六个分别用动稳定度、残留稳定度、破坏时最大弯拉应变、模量、碾压12000次时的车辙深度、应力比0.3时的疲劳寿命表示，其中车辙深度是极小型指标，其余指标均为极大型指标。

2 高模量沥青混合料综合性能指标权重的确定

本文首先采用层次分析法求解各性能指标的主观权重，为了避免专家的主观意愿造成决策中出现极端值，影响整体评价结果，本文并通过组合数有序加权算子（C-OWA）对决策数据进行主观权重的修正，并结合熵权法进行各指标客观赋权，消除主观因素造成的偏差，将主客观赋权法得到的权重通过线性加权法进行组合，使最终的权重既能反映决策者的主观期望，又能客观地体现各指标的权重。

2.1 AHP — C-OWA 法确定主观权重

2.1.1计算初始权重矩阵

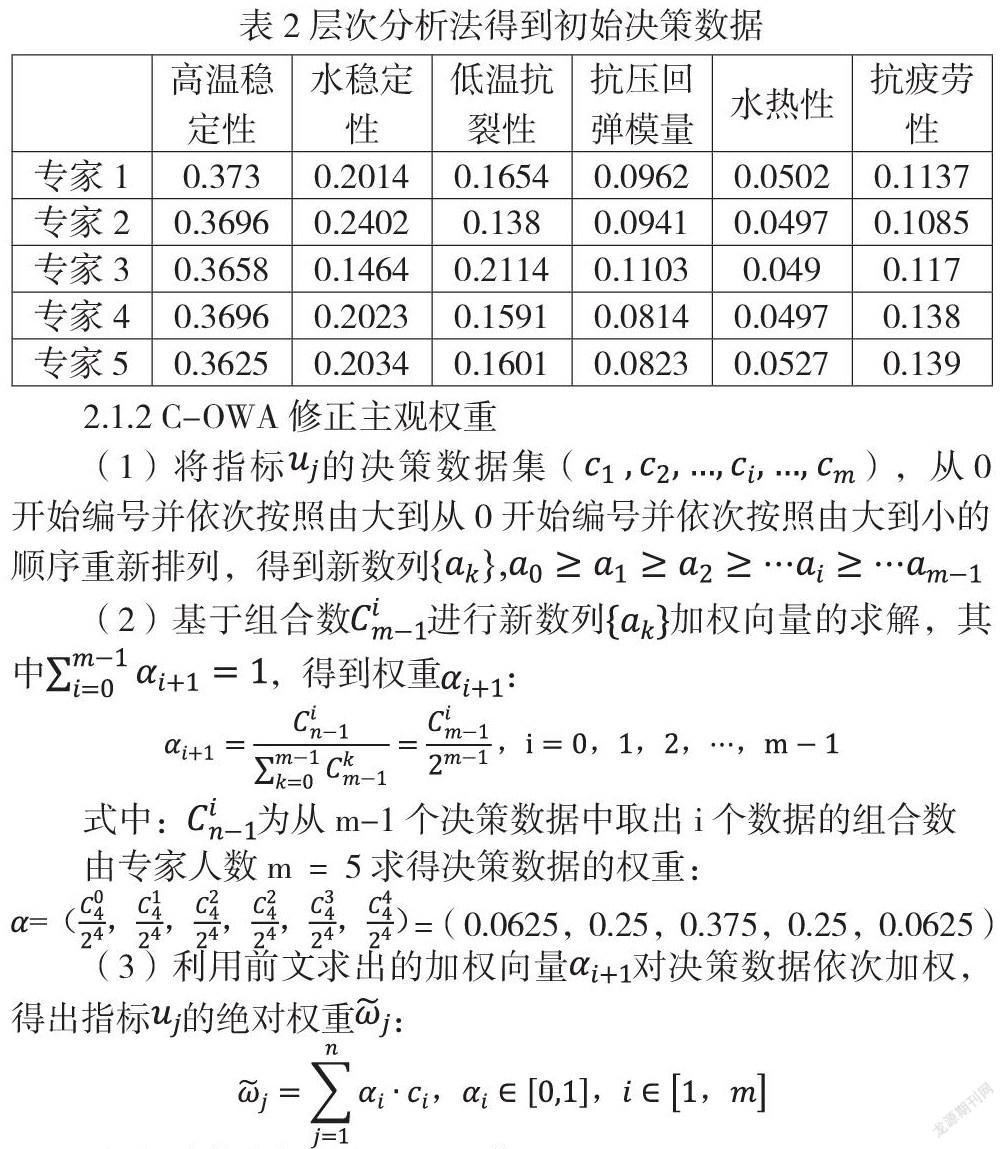
本文评价指标体系共采用六个指标，评价矩阵为。邀请相关领域的5位专家对各综合性能评价指标进行比较，得出比较矩阵，利用层次分析法，得出每个专家对各指标的不同的权重，所得结果均通过一致性检验，进而获得5位专家对6个评价指标的初始权重矩阵，详细数据见表2。

2.1.2 C-OWA修正主观权重

（1）将指标的决策数据集（），从0开始编号并依次按照由大到从0开始编号并依次按照由大到小的顺序重新排列，得到新数列

（2）基于组合数进行新数列加权向量的求解，其中，得到权重：

由专家人数m=5求得决策数据的权重：

（3）利用前文求出的加权向量对决策数据依次加权，得出指标的绝对权重：

（4）计算指标的相对权重值：

通过依次进行上述计算步骤，即可得到基于AHP—C-OWA法对高模量沥青评价指标的主观权重：W1=（0.370 0.202 0.164 0.092 0.050 0.123）

2.2 熵权法确定客观权重

（1）计算标准化矩阵，对极大型指标和极小型指标进行标准化处理，本文中除代表水热性的车辙深度是极小型指标外，其余指标均为极大型指标。求正向化矩阵时，对于车辙深度的正向化方法时用20mm减去对应的车辙深度转化为正向指标，设初始矩阵为X，矩阵元素为，标准化矩阵为D，矩阵元素为

（2）计算第 j 项指标下第 i 个样本所占的比重，得到数据的概率矩阵。

（3）计算每个指标的信息熵以及信息效用值，通过归一化得到每个指标的熵权。对于第j个指标而言，信息嫡的计算过程为：

客观权重向量为：

通过依次进行上述计算步骤，即可得到基于熵权法对高模量沥青评价指标的客观权重：

2.3 确定组合权重

将主客观赋权法得到的权重通过线性加权法进行组合，获得组合权重W作为最终指标权重：

式中，本文中，得到指标的组合权重为：W=（0.305 0.178 0.153 0.113 0.106 0.145）

3基于TOPSIS-灰色关联度的沥青综合性能评价

本文在建立沥青性能评价指标体系的基础上，将TOPSIS法和灰色关联理论与结合，弥补两种方法本身的不足，使不同RK300改性剂掺量方案的选择更加合理可信。

（1）經过无量纲化处理，构成无量纲矩阵为，无量纲化处理过程如下：

（2）组合权重与无量纲矩阵相乘，得到加权标准化矩阵为：

其中为n个评价指标所占的权重。

（3）求出加权标准化矩阵的正理想解和负理想解。是每列最大值构成的最优向量，是每列最小值构成的最差向量。

（4）计算各方案与和的欧式距离。

（5）计算样本和的灰色关联度。

其中，为分辨系数，一般取最为恰当，本文中。与和的灰色关联矩阵分别是，于是样本i与正理想样本的关联度为

样本 i 与负理想样本的关联度为

（6）对欧式距离和灰色关联度进行标准化处理

（7）计算灰色关联相对贴近度并排序

根据ξ大小进行排序，其中，其中分别为樣本与和的贴近程度，是偏好系数，，本文取。

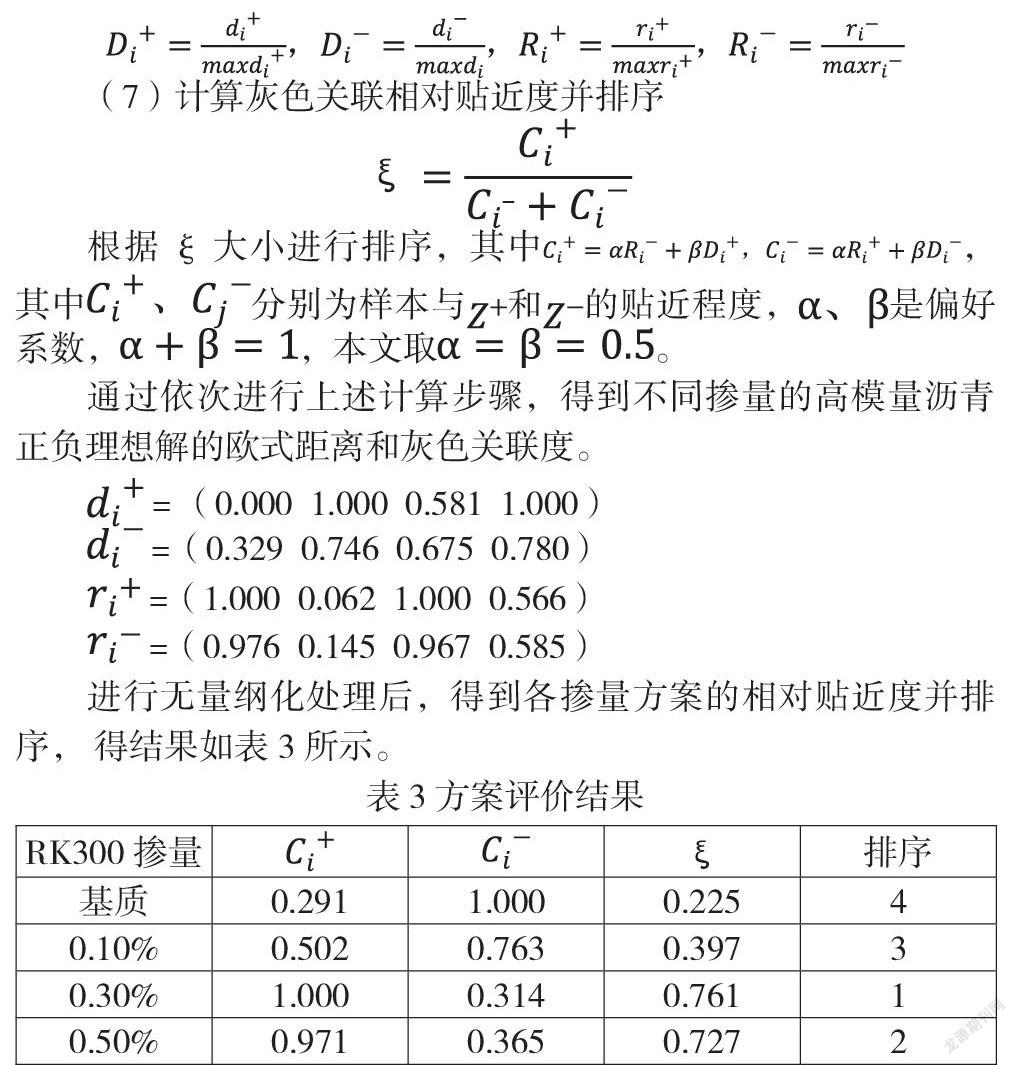
通过依次进行上述计算步骤，得到不同掺量的高模量沥青正负理想解的欧式距离和灰色关联度。

进行无量纲化处理后，得到各掺量方案的相对贴近度并排序， 得结果如表 3 所示。

由表3的相对贴近度都在0.2-0.8之间， 排序为 0.30%> 0.50%>0.10% > 基质，0.30%的RK300高模量沥青混合料贴近度最优，故可知RK300改性剂的掺量最优为0.30%。

4 结语

本文结合相关文献，构建了高模量沥青混合料综合性能评价体系，利用组合赋权法，将AHP — C-OWA 法得到的主观权重与熵权法得到的客观权重通过线性组合，得到最终的组合权重，避免主观偏好。将TOPSIS和灰色关联模型相结合，定义了新的相对贴近度并求解，对方案进行排序及择优选择。本文建立的评价模型科学合理，对解决沥青综合性能评价问题具有现实意义。

参考文献：

[1] 佟波. RK300高模量沥青混合料的路用性能研究[D].沈阳建筑大学，2016.

[2]林俐，王腾志，吕奕波，曲绍杰，高重晖.基于组合权重-灰云聚类模型的配电网调度运行管理水平综合评价[J/OL].华北电力大学学报（自然科学版）：1-11[2021-06-08]

[3] 周衍平，李蓓仪.创新型企业知识产权质押融资风险评价——基于灰色关联TOPSIS模型[J].山东科技大学学报（社会科学版），2020，22（06）：71-79+91.

[4]吴晓.基于优劣解距离法与灰色关联融合的油田节能技术优选[J].化学工程与装备，2020（11）：38-41+43.

[5]赵金先，蒋克洁，陈涛，孟玮.基于C-OWA算子赋权的地铁PPP项目融资风险灰色聚类评价[J].青岛理工大学学报，2021，42（02）：128-137.

[6]李慧民，熊雄，董美美，熊登，周崇刚.基于灰色关联改进TOPSIS法的既有建筑抗震加固方案优选[J].重庆理工大学学报（自然科学），2020，34（12）：264-270.

[7]司守奎，孙兆亮 数学建模算法与应用[M] 北京 国防工业出版社 2017

作者简介：李辉（2000-07）女，汉族，河北衡水，本科在读，石家庄铁道大学，研究方向：交通方向-路基路面-高模量沥青