智能制造背景下复杂供应商网络协同评价研究
张明昊 闻波 石梅 卓翔芝






摘要:为促进核心制造企业与旗下供应商之间形成紧密的协同关系,从复杂供应商网络的结构特征入手,根据其无标度和小世界的结构特点,将宏观的复杂供应商网络切割拆分为以局部网络中最大hub节点为顶点的多个微观子网络。从系统的视角出发,将熵权法与TOPSIS法相结合,建立了基于熵权TOPSIS法的子系统协同评价模型。研究结果表明,该模型能够有效的对子系统的协同状态做出评价,有助于核心制造企业科学合理的管理供应商网络。
关键词:智能制造;协同效率;复杂网络;熵权法;TOPSIS法
中图分类号:F203
文献标志码:A
收稿日期:2020-10-26
基金项目:
安徽省高校自然科学基金(批准号:KJ2018A0395;KJ2019A0959;KJ2019B04)资助。
通信作者:
闻波,男,副教授,主要研究方向为信息管理。E-mail:wbthinkly@163.com
随着大数据、物联网为代表的新兴信息技术在工业领域中的渗透,中国产业变革的进程不断加快, “智能制造”这一信息化和工业化深度融合的产物成为衡量全球制造业阶段水平的风向标[1-3]。为加快中国向制造强国转变,国务院印发了“中国制造2025”计划,受到众多学者的关注和重视[4]。智能制造背景下,制造企业将供应商视为其生产系统的延伸[5]。供应商扮演的角色不仅是物料的供给者,也作为制造企业的重要合作伙伴参与到产品的研发和制造环节,为制造企业分担一定风险的同时分享相应的收益。制造企业也在与供应商连续动态的业务交流中获得了供应商所匹配的资源及创新要素,进而推动制造企业战略目标的实施和产品竞争力的提升[6]。互惠双赢的局面促使制造企业与供应商的联系日益密切,制造企业也愈发依赖供应商来维持企业的竞争优势[7],形成了以制造企业为核心,供应商为边缘节点的供应商网络[6]。源于供应商网络中主体间的竞争关系,以及不同主体在经营策略和利益需求上存在差异,企业在具体业务流程的衔接和匹配上无法实现有效的协同。此外,信息的不透明、不对称极易引发目标冲突和机会主义风险[7-8],同样使得企业间的协同难以按照预期的方向发展,少量能够成功实施供应商网络协同的企业在协同绩效的度量上再次陷入了困境。近年来,以复杂系统理论研究供应链网络引起了学术界的广泛关注[9]。陈晓等[10]认为供应链系统是一种复杂的自组织、自适应性网络系统,复杂网络的研究方法有利于揭示该类系统的特质。范碧霞等[11]从供应网络复杂性产生的原因及特征入手,分析得出復杂网络理论具有帮助企业更好地评价供应链结构、协调成员企业行为、提高供应链稳定性以及优化供应链的功能。随着研究的深入,有学者尝试对已有模型改进创新,如指出供应链网络中节点的连接数量和连接速率并非仅与时间因素有关[12],还受到节点之间吸引力大小[13]、位置参数[14]、边效益[15]、供应链生命周期[16]等因素的影响,提出了基于X因素的复杂供应链网络演化模型。从不同视角对供应链网络展开的研究表明当前的供应链网络已摆脱简单拓扑结构形态,具备复杂网络的特征。因此,由核心制造企业和供应商所构成的供应商网络作为供应链网络中的重要组成部分同样具备相应的复杂网络特征,从而使得本文以复杂网络理论为框架对供应商网络协同进行研究具有可行性。针对当前复杂供应商网络中的企业在协同方面存在的问题,本文依据复杂供应商网络的结构特征对其进行切割,将其划分为多个以制造企业为核心的微观子网络,在此基础上借助在多属性领域决策领域有良好表现的熵权法和TOPSIS评价方法构建评价模型,对不同子网络模块的协同状况做出评价,帮助核心制造企业科学、合理、有效的管理供应商网络。
1 复杂供应商网络
真实世界中规则网络的占比很小,很多实际问题抽象出的网络呈现出复杂网络的形态。供应链的形态对其自身的性能有着重要影响,由于早期的链式供应链以及由其扩展形成的供应链网络已经无法描述和解释企业间错综复杂的交互关系,为适应当前多变的环境和未来的发展趋势,传统供应链网络已逐步向复杂网络转变[17-18]。为了帮助核心制造企业与旗下供应商开展高效的协同运作并取得增殖的协同效益,继而在动态多变的市场环境下保持足够的竞争力,本文将对研究的框架进一步聚焦。结构和功能完整的供应链一般由制造商、供应商、分销商、零售商以及最终消费群体五部分组成,其中产品的价值增值是通过供应链的多层级传递实现的,在此过程中涉及多个制造和供应环节。与仅在供应链终端占有一定份额的零售商和分销商相比较,供应商和制造商拥有绝对的数量优势,故对复杂供应链网络削减一定数量的分销模块节点不会对网络整体的形态和功能产生影响。剔除分销商、零售商和顾客,本文的研究建立在复杂供应商网络框架下。复杂供应商网络是围绕核心制造企业,建立在与多个供应商之间达成密切合作关系的基础上,具有小世界和无标度结构特征的供应体系[19]。Barabási等[12]的研究表明,复杂网络的连接度在现实问题中有幂率分布的特征,且幂指数通常在2~3的区间内,统计特性呈现幂率分布的复杂网络被称为无标度网络。无标度网络具有极大的异质性,各节点的连接不服从均匀分布,大部分的节点只有少量的连接,度值很低,但存在少数度值极高的中枢节点(hub节点)拥有大量的连接,且对整个网络的运行和维持起着至关重要的作用。供应商网络中散布着多家核心制造企业,核心制造企业通过供需关系与旗下的供应商建立联系,形成围绕核心制造企业展开的从产品原材料供应到生产加工,以及销售运输的产品价值链,充分体现了无标度性[10]。与此同时,科技的进步为世界经济与贸易提供便利,企业能够忽略地理位置因素的影响实现实时的信息沟通。供应商网络中的核心制造企业扮演着桥梁的角色,为不同类别的供应商之间建立联系,使得供应商网络在结构上具有局部集聚效应,表现出明显的小世界特性[20-21]。
2 评价模型构建
经济全球化发展使企业间合作愈发密切,同时也加深了供应链成员企业之间的角色重叠和关系复杂度。相同的企业可能在不同的供应链中扮演着不同的角色,如制造企业在负责生产的同时也发挥着供应商的功能。为消除该现象对研究的影响,本文从复杂供应商网络的结构特征入手,根据其无标度和小世界的结构特点,将宏观的复杂供应商网络切割拆分为多个以局部网络中的核心制造企业为顶点、向四周方向辐散的微观子网络,其中每个子网络中包含一个核心制造企业和若干个供应商,如图1所示。通过对复杂供应商网络的拆分,实现了对复杂三维立体网络空间的结构由繁向简的转化,研究量级上的巨大转变使得模型的构建更为简明直观。因系统是由相互作用、相互依赖的若干部分组成的具有特定功能的有机整体[22],故可将复杂供应商网络映射为系统,经切割产生的微观子网络与复杂供应商网络之间为子母系统关系。
对子系统中的节点进行同向化处理,将散布在hub节点周围的子节点旋转、牵拉至hub节点的下方,使隶属于不同供应层级的节点在结构模型中的位置相对统一。在此基础上,为进一步简化结构模型,将经同向化处理后的子节点置于与hub节点相同的平面内,实现结构模型由三维立体向二维平面的过渡。由图2所示,子系统在结构上具有自相似的特征,即局部形态与整体形态相似,局部中又存在着相似的局部,不断地重复、层层嵌套形成分形图。
2.1 熵权法
信息熵[23]是根据事物本身对信息的贡献度来描述信源不确定性的度量工具。指标的信息熵越小,说明其变异程度越大,即能够提供的信息越多,对系统的贡献度也就越大[24-25]。该特性使得熵权法被广泛应用于求解多属性决策问题中的属性权重部分。
Step 1 以一个多属性决策问题为例:设有n个评价对象,m个评价指标,对于原始数据矩阵A=aijn×m,aij表示第i个评价指标的第j项指标评价值。为解决各指标的计量单位不一致问题,对原始数据矩阵A做同质化处理,得到数据矩阵B=bijn×m;
Step 2 对数据矩阵B做归一化处理,得到指标评价矩阵C=cijn×m,其中, cij=bij∑ni=1bij,∑cij=1,i=1,2,…,n,j=1,2,…,m;
Step 3 计算第j项指标的熵值: ej=-k∑ni=1cijln cij,其中k=ln n-1,0≤ej≤1,j=1,2,…,m,求解过程中,若cij=0,则cijln cij=0;
Step 4 计算得到各指标的权系数:wi=(1-ej)/(m-∑mj=1ek)。
2.2 基于熵权TOPSIS法的协同评价模型
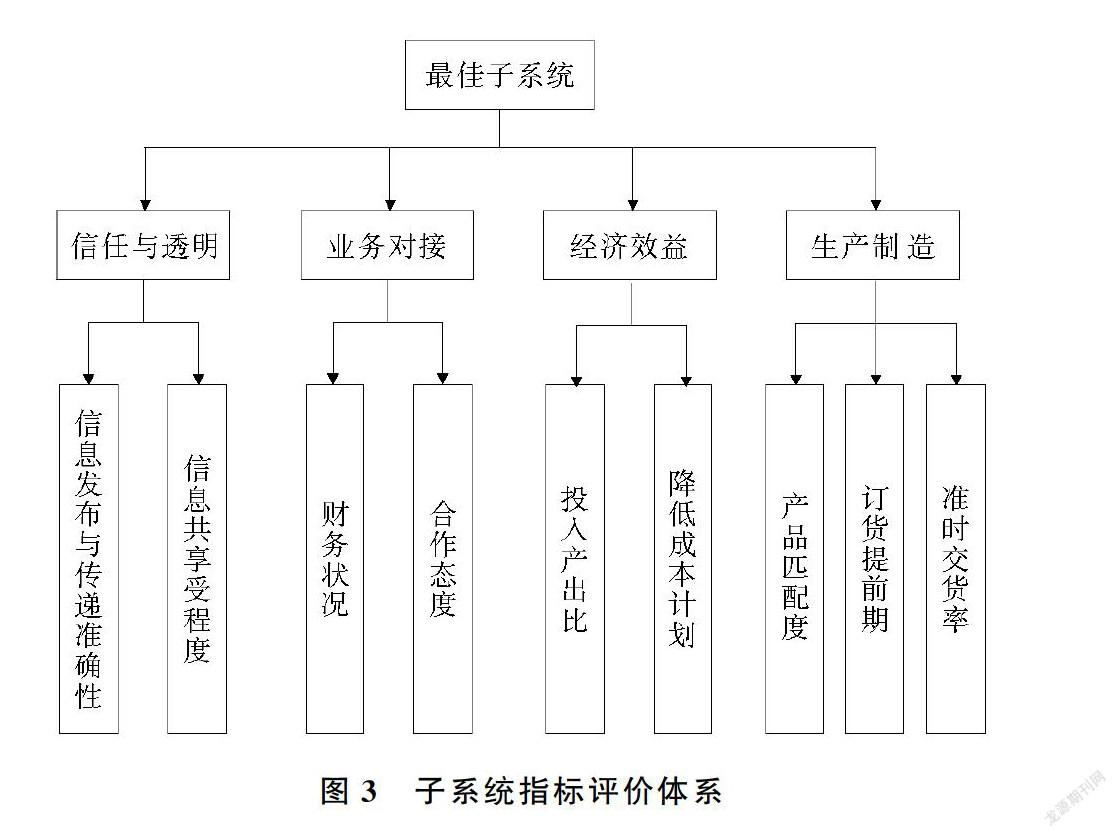
TOPSIS 法[26](Technique for Order Preference by Similarity to an Ideal Solution)是一种常用的组内综合评价方法,根据有限个评价对象与理想化目标逼近程度的排序结果对多属性决策过程中的备选方案进行优劣抉择[27]。理想化目标是正理想解与负理想解这一对相反概念的合称。正理想解为目标的最优解,即各评价指标均达到最好的预期;负理想解为目标的最劣解,即各评价指标均达到最差的预期。当某一备选方案在最逼近正理想解的同时又最远离负理想解,则该方案为最佳方案[28]。在对各子系统的协同状况进行评估前,需要建立具备科学合理、可操作性强、系统全面、独立无交叉特征的指标评价体系。将指标体系划分为三级:方案层、一级指标层和二级指标层,规定所有指标类型为效益型。指标的选取建立在曾明華[29]等所构建的供应商协同能力评价指标体系的归纳总结基础上,其中一级指标包括信任与透明、业务对接、经济效益和生产制造四个方面;二级指标包括信息发布与传递准确性、信息共享程度、财务状况、合作态度、投入产出比、降低成本计划、产品匹配度、订货提前期、准时交货率九个方面,见图3。
设共有y个评价对象,每个评价对象有z个评价指标。对于原始数据矩阵E=euvy×z ,euv代表第u个评价对象的第v个指标评价值。指标评价值在0~10的区间内取值,其中10为最优值。
Step 1 对原始数据矩阵E做比值归一化处理,得到指标评价矩阵E′=puvy×z,其中, puv=euv∑yu=1euv,∑puv=1,u=1,2,…,y,v=1,2,…,z;
Step 2 对指标评价值矩阵E′做加权处理,得到加权指标评价矩阵F=fuvy×z,其中, fuv=xu·puv,xu=1-αuz-∑zk=1αk, αu=-k∑yu=1puvln puv,k=ln y-1, 0≤αu≤1,u=1,2,…,y,v=1,2,…,z,若puv=0,则puvln puv=0;
Step 3 确定评价对象的最优解和最劣解。最优解由矩阵F中每列元素的最大值构成,最劣解由矩阵F中每列元素的最小值构成:
f+=maxf11,f21,…,fy1,maxf12,f22,…,fy2,…,maxf1z,f2z,…,fyz
=f+1,f+2,…,f+z
f-=minf11,f21,…,fy1,minf12,f22,…,fy2,…,minf1z,f2z,…,fyz
=f-1,f-2,…,f-z
Step 4 分别计算出方案解与最优解的距离d+u以及与最劣解之间的距离d-u: d+u=∑zv=1fuv-f+v2,d-u=∑zv=1fuv-f-v2,u=1,2,…,y;
Step 5 计算方案解与最优解的贴近度: cu=d-ud+u+d_u,0≤cu≤1,u=1,2,…,y;
Step 6 对Step 5所取得的接近度cu的数值进行大小排序,cu的值越大,说明评价对象越优,由此得到最佳子系统。
3 案例分析
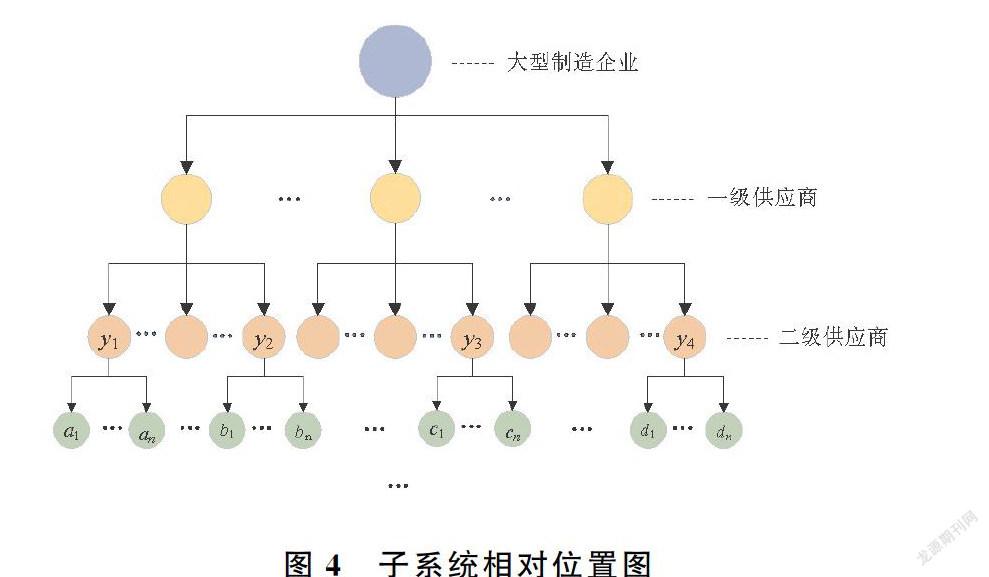
考虑到在智能制造背景下,大型制造企业因生产、办公等需要,与其建立合作关系的供应商数量往往十分庞大。受到数据获取方面的限制,本文从某大型制造企业的二级供应商中选取四家规模较小的制造企业
y1、y2、y3和y4作为案例分析中的核心制造企业(供应链中的多数企业既是供应商也是制造商),该组企业位于安徽省淮北市,企业下属供应商5至10家不等,对四家制造企业与旗下供应商所构成的子系统分别记作Y1、Y2、Y3和Y4,见图4。
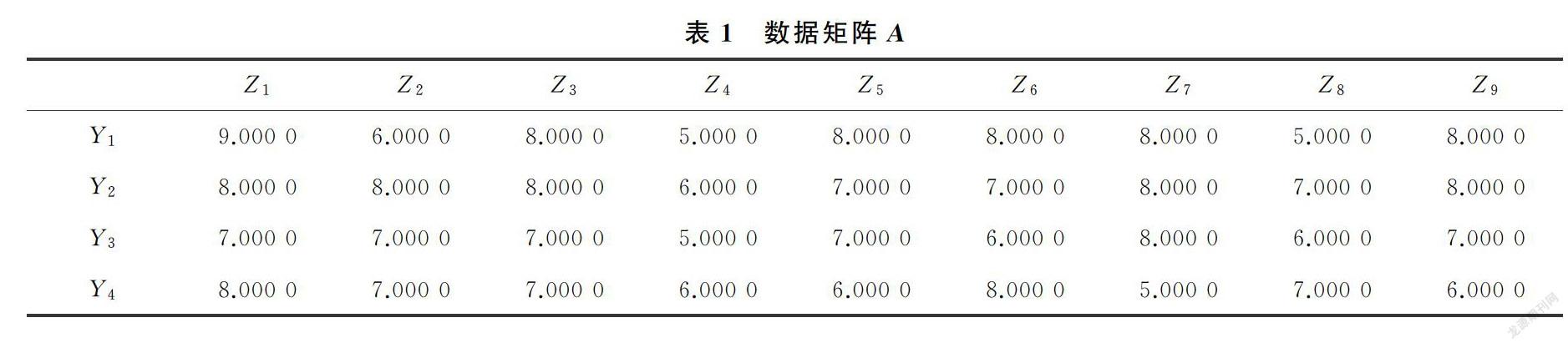
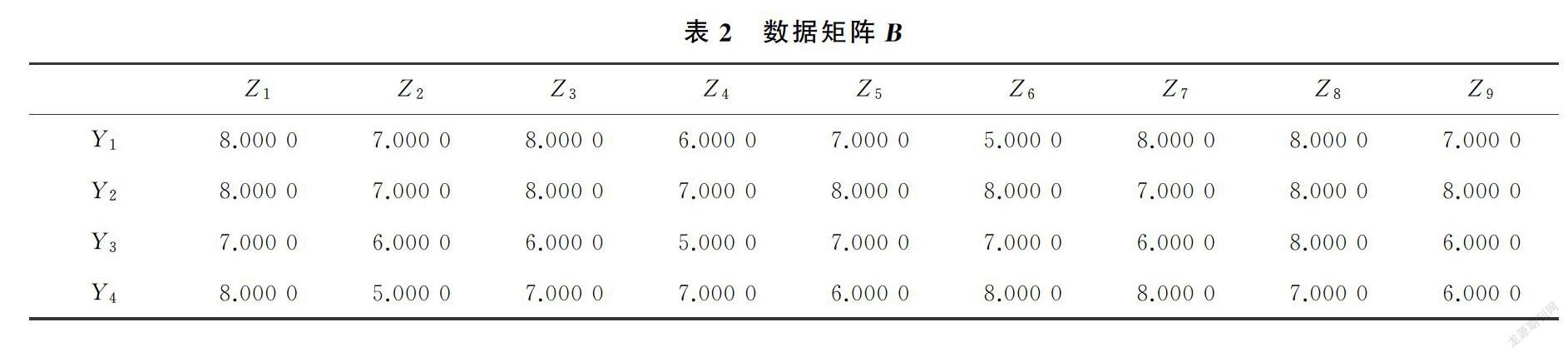
邀请3位有不同专业背景、来自不同管理和技术岗位的业内专家按照图3所建立的指标评价体系打分,不同专家给予评价的影响力相同,指标评价值在0~10的区间内取值。经专家评定生成的数据矩阵A、B和C,如表1、表2、表3所示。
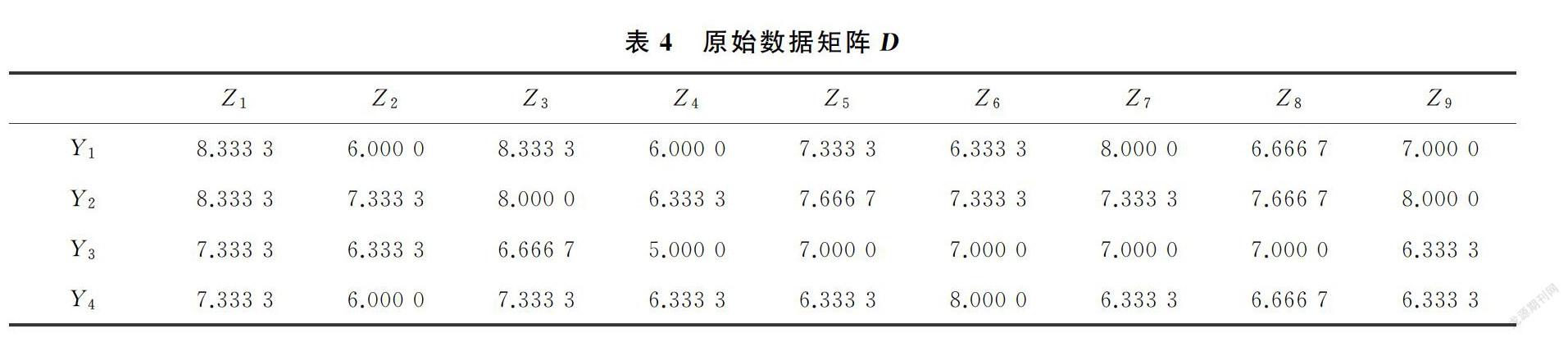
对数据矩阵A、B和C中的评价指标打分结果求平均值,得到原始数据矩阵D,见表4。
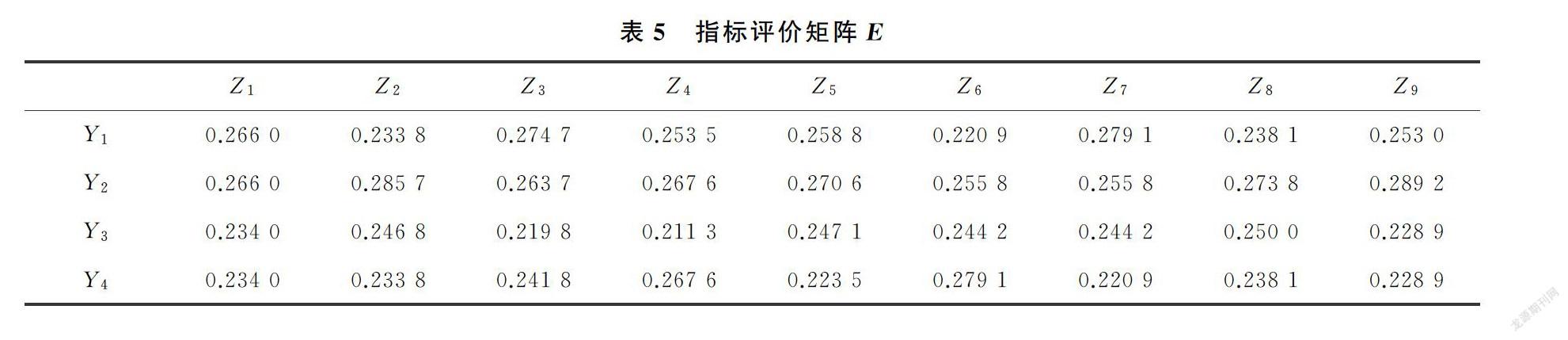
借助Matlab-R2017a软件编写相关程序代码,获得以下数据(精确到小数点后四位)。原始矩阵D经比值归一化处理后得到的规范后的指标评价矩阵E,见表5。
(1)评价指标的熵值α1~α9分别为: α1=0.998 5,α2=0.997 4,α3=0.997 4,α4=0.996 8,α5=0.998 2, α6=0.997 5,α7=0.997 5,α8=0.998 8,α9=0.996 6;
(2)指标权重x1~x9分别为: x1=0.069 1,x2=0.119 8,x3=0.121 9,x4=0.149 2,x5=0.083 0, x6=0.119 4,x7=0.119 4,x8=0.056 8,x9=0.161 5;
(3)對规范化后的指标评价值矩阵E做加权处理,得到规范化后的加权指标评价矩阵F,见表6。
(4)评价对象的最优解和最劣解为: f+=(0.0184,0.0342,0.0335,0.0399,0.0225,0.0333,0.0333,0.0155,0.0467),f-=(0.0162,0.0280,0.0268,0.0315,0.0186,0.0264,0.0264,0.0135,0.0370);
(5)评价对象到最优解和最劣解的距离分别为: d+1=0.011 4,d+2=0.004 1,d+3=0.016 6,d+4=0.014 9,d-1=0.012 7,d-2=0.017 1,d-3=0.004 7,d-4=0.011 2;
(6)评价对象与最优解的贴近度分别为: c1=0.526 5,c2=0.804 6,c3=0.220 2,c4=0.429 7;
由贴近度的大小可知,子系统Y1~Y4的评价结果按照Y3<Y4<Y1<Y2的顺序排序,即Y2为最佳评价对象,Y1与Y4次之,Y3最差。
对上述案例分析过程进行分析,表4中协同指标的打分结果能够直观地反映出子系统中核心制造企业与旗下供应商在各方面的协同状况,核心制造企业可有针对性地对其中分值较低的协同项进行强化,以提高整体协同效率。此外,由协同评价指标的熵值和权重可知,除Z1、Z5以及Z8这三项指标所占比重较低,Z4与Z9两项指标较所占比重较高外,其他指标对于子系统评价模型的贡献度较为平均,说明信息发布与传递稳定性、投入产出比以及订货提前期这三项指标在各子系统中的评价结果差异较小。而合作态度与准时交货率两项指标的评价结果差异较大,评估方可籍此横向比较并统计各子系统的协同指标分值,向核心制造企业提供各协同指标的行业均值作为管理参考。
4 结论
本文基于熵权TOPSIS法构建的子系统协同评价模型,旨在突出复杂供应商网络中不同子网络模块的成员企业在协同配合度方面的差异。通过对子系统协同评价指标熵值变化的阶段性监测,核心制造企业能够有效的获取和掌握各子系统内部不同方面的协同状况,便于核心制造企业针对其中的薄弱环节采取措施进行巩固和加强。相关政策制定部门可对评价得到的最优子系统开展有指向性研究,深度挖掘其组织结构、协作方式等方面特征,从中提取有借鉴价值的信息向全社会做普适性的推广。由于本文未能对子系统内部成员企业之间的协同机制进行剖析和量化,评价结果在精确度方面具有一定的局限性,未来需在此基础上建立协同度量模型,通过数学模型对子系统内部成员之间的协同过程进行刻画以提高准确性。
参考文献
[1]丁雪红,石莉,李敏,等.基于BP神经网络的智能制造能力成熟度评价研究[J].青岛大学学报(自然科学版),2019,32(3):20-25+30.
[2]ZHOU G. Knowledge-driven digital twin manufacturing cell towards intelligent manufacturing[J]. International Journal of Production Research, 2020, 58(4): 1034-1051.
[3]王友发,周献中.国内外智能制造研究热点与发展趋势[J].中国科技论坛,2016(4):154-160.
[4]周济.智能制造——“中国制造2025”的主攻方向[J].中国机械工程,2015,26(17):2273-2284.
[5]李随成,王玮,禹文钢.供应商网络形态构念及实证研究[J].管理科学,2013,26(3):19-30.
[6]GAO G Y, XIE E, ZHOU K Z. How does technological diversity in supplier network drive buyer innovation? Relational process and contingencies[J]. Journal of Operations Management, 2015, 36(1): 165-177.
[7]HAMERI A P, PAATELA A. Supply network dynamics as a source of new business[J]. International Journal of Production Economics, 2005, 98(1): 41-55.
[8]李娜,李随成.面向供应商網络的企业网络化行为:多维结构探索研究[J].科技进步与对策,2017,34(19):15-21.
[9]张轶,钱晓东.基于复杂网络的供应链建模及仿真研究[J].科技管理研究,2014,34(22):183-186.
[10] 陈晓,张纪会.复杂供需网络的局域演化生长模型[J].复杂系统与复杂性科学,2008,5(1):54-60.
[11] 范碧霞,刘帅.复杂网络理论在供应链管理中的应用研究[J].商业经济研究,2017(18):97-98.
[12] BARABSI A L. Emergence of scaling in random networks[J]. Science, 1999, 286(5439): 509-512.
[13] 陶少华,杨春,李慧娜,等.基于节点吸引力的复杂网络演化模型研究[J].计算机工程,2009,35(1):111-113.
[14] 赵志刚,周根贵,潘瑞芳.基于位置吸引力的加权复杂供应链网络局域世界演化模型研究[J].计算机科学,2018,45(12):71-76.
[15] 曹文彬,熊曦.边效益因素下复杂供应链网络局域演化机制[J].计算机应用研究,2016,33(1):75-77+81.
[16] 丁飞,陈红,杨冀豫.基于复杂网络的供应链网络演化模型研究[J].计算机与数字工程,2018,46(2):343-347.
[17] 张昕瑞,王恒山.复杂供应链网络结构模型研究[J].工业技术经济,2008(2):79-81.
[18] 张昕瑞,王恒山.供应链网络的价值增值博弈决策研究[J].商业经济与管理,2009(7):29-35.
[19] WATTS D J. Collective dynamics of small-world networks[J]. Nature, 1998, 393(6684): 440-442.
[20] 吕波,韩健,凡新凯.新技术革命背景下基于SIR-SCR模型的供应链风险传导新机理研究[J].科技管理研究,2020,40(5):199-206.
[21] 刘纯霞,舒彤,汪寿阳.基于小世界网络的供应链中断风险传导过程研究[J].商业经济与管理,2015(5):24-30.
[22] 钱学森.论宏观建筑与微观建筑[M].杭州:杭州出版社, 2001.
[23] SHANNON C E. A mathematical theory of communication[J]. The Bell System Technical Journal, 1948, 27(4): 379-423.
[24] MAVI R K. Supplier selection with Shannon entropy and fuzzy TOPSIS in the context of supply chain risk management[J]. Procedia - Social and Behavioral Sciences, 2016, 235: 216-225.
[25] 仝金强.基于熵权TOPSIS法的舰船设计方案评估[J].实验室研究与探索,2018,37(1):9-12.
[26] HWANG C L, YOON K. Multiple attribute decision making[J]. Lecture Notes in Economics & Mathematical Systems, 1981, 404(4): 287-288.
[27] 林龙圳,李达,林震.基于熵权-TOPSIS模型的库布齐沙漠地区水资源承载力评价[J].华中师范大学学报(自然科学版),2020,54(4):640-648.
[28] 董培培,王磊.基于FBWM的绿色物流供应商评价研究[J].青岛大学学报(自然科学版),2019,32(3):53-61.
[29] 曾明华,王吟松,杨晓光.供应商协同能力评价指标体系研究[J].计算机工程与应用,2014,50(4):18-23.
Research on Collaborative Efficiency Evaluation of Complex Supplier
Network Under the Background of Intelligent Manufacturing
ZHANG Ming-haoa , WEN Bob , SHI Meib , ZHUO Xiang-zhia
(a. College of Economics and Management, b. College of Computer
Science and Technology, Huaibei Normal University, Huaibei 235000, China)
Abstract: The purpose is to promote the formation of close collaborative relationship between core manufacturing enterprises and their suppliers. According to the scale-free and small world structure of complex supplier network, the macro complex supplier network is divided into several micro sub networks with the largest hub node in the local network as the vertex. From the perspective of system, the entropy weight method and TOPSIS method are combined to establish a subsystem collaborative evaluation model based on entropy weight TOPSIS method. The results show that the model can effectively evaluate the collaborative state of subsystems, and help the core manufacturing enterprises to manage the supplier network scientifically and reasonably.
Keywords:
intelligent manufacturing; collaborative efficiency; complex network; entropy weight; TOPSIS method

