数学建模在接触式轮廓仪标注中的应用

摘要：接触式轮廓仪在接触测量时，探针存在沾污、缺陷、扫描位置不准等问题，降低了工件轮廓曲线的测量精度。为此，运用阈值思想zli -（kli xi+ bli）≥δi 求解轮廓曲线的重要参数，采用Matlab插值法对数据进行归一化处理。通过研究得到的各项参数值及完整轮廓线表明，数学建模方法针对扫描探针、物品位置等问题所造成的误差能够进行较好的修正。

关键词：轮廓仪;拟合;阈值;插值;旋转坐标

中图分类号：O29

文献标志码：A

收稿日期：2021-01-08

基金项目：

国家自然科学基金（批准号：51774008;51974007;51874002）资助，安徽省自然科学基金（批准号：KJ2018A0715）资助。

通信作者：

冯英华，女，副教授，主要研究方向为数学与应用数学。E-mail：278894811@qq.com

接触式轮廓仪作为一种精密的测量仪器，用于测量工件的表面几何形状，工作原理是触针滑过工件表面时，获得其轮廓参数，便于测量如沟、孔、槽等复杂的工件表面，所以在制造业中得到广泛的应用。轮廓的理想曲线應该是光滑的，但在实际工作中，由于存在探针沾污、探针缺陷、扫描位置不准等问题，检测到的轮廓曲线呈现出粗糙不平的情况，使得测量结果产生误差[1-3]。近年来，在对接触式轮廓仪的标注问题中，国内外学者做了很多研究，主要表现为建立数学模型和回归分析[4-6]：高瑞翔[7]利用余弦误差分析了其校准结果的影响程度以及其影响趋势。贾宁[8]在非球面斜率测量误差的基础上建立一种补偿模型。一些学者从准确性和稳定性等方面进行了研究，并提出不同的解决方法，王旭刚等[9]使用轮廓仪测量双半内圈沟曲率的新方法，解决了轮廓仪测量双半内圈沟道曲率时，测量准确率低和重复性不好的问题。韩志国等[10]利用在偏移量为-150～150μm内探针判断出轮廓仪存在探针缺陷和扫描位置不准的问题。Whitehouse[11]在触针扫描系统上建立数学模型通过蚁群算法补偿测量误差。Forbes[12-14]提出了一种非球面Q-type函数多项式数学表征形式的检测方法。Indrasis等[15]利用光学表面轮廓仪在不锈钢微型通道上进行了表面形貌测量，分析了表面粗糙度对局部和全局无量纲性能参数的影响。综上，关于接触式轮廓仪检测工件轮廓线的误差分析、准确性等理论的研究已经比较深入，但是结合待测体的轮廓变化特点，对工件的轮廓线转折角度和转折点的研究比较少。因此，本文运用阈值思想，利用Matlab插值法和回归分析法求解工件的轮廓曲线，并从归一化的角度来解决数据不稳定的特点，进而得出各项参数值并作出工件局部以及完整的轮廓曲线，为工件轮廓线的标注问题提供更多可参考的方法。

1 工件水平放置下轮廓曲线的求解

1.1 求解l1所在的直线方程

先做出l1的局部图，假设此段部分可以近似看成水平线段，取其极差近似值0.01，均值近似值-1.77，且假设在范围 （-1.775， -1.765）之间都可视为l1的部分。

求解第一个转折点A1的坐标，根据假设，利用Excel计算各测量数据的纵坐标zli与均值-1.77的差值是否在-0.005，0.005的范围内

-0.005≤zli--1.77≤0.005（1）

因此 A1点坐标记为49.775 38，-1.77。l1的方程记为：y=-1.77，46.596≤x≤49.766。

1.2 转折点坐标的求解

计算所有点坐标中满足-0.005≤zli--1.77≤0.005的点，并求出所有测量点中在此区间上点的个数为93 798，占比为24.42%，因此我们不妨假设其他所有水平线段均在l1所在的直线上，再利用式（1）以及Excel的筛选功能，类似计算A1的方法，计算各转折点Aii=1，…，15的横坐标，见表1。

1.3 各槽口宽度及水平线段长度求解

由于各转折点处于同一条水平线上，槽口宽度及水平线段长度等于横坐标的差，见表2。

2 工件倾斜放置下轮廓曲线的求解

2.1 利用旋转后点的坐标公式

旋转后的坐标公式为

x1y1=cosθsinθ-sinθcosθxy（2）

将原坐标（xdi，zdi）进行旋转水平化，得到校正后轮廓线的坐标并且绘制轮廓线，并和工件旋转前以及水平放置的曲线进行作对比。如图1所示。

求出水平位移误差Δ=（0.99xd1-0.128 7zd1）-xl1=1.518 808，并利用轮廓线修正后的坐标值求解各项参数。

2.2 工件倾斜角度的求解

根据水平线段均在同一水平直线上可知，倾斜后的也应在同一直线上，利用（xdi，zdi）作出散点图，从图上先粗略取值ldi各中点坐标（di，di）如表3所示，用这些点的坐标并且利用Excel拟合出ld所在的直线方程y=-0.129 8x+7.736 4。倾斜角为θ=π-arctan 0.129 8=172.6°。

2.3 工件完整轮廓线的求解

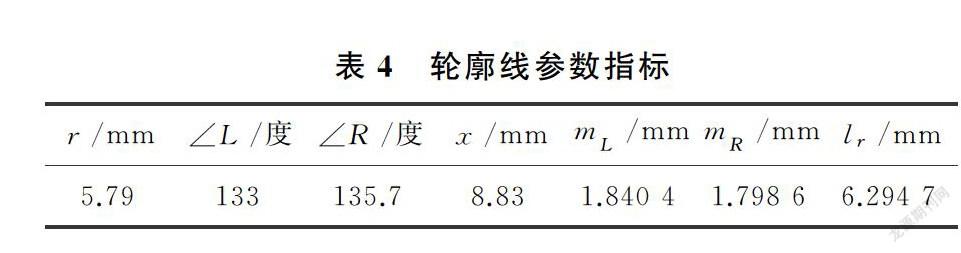
利用式（2）曲线旋转的求解方法得到倾斜图形校正后的曲线（用Ωi表示），其中Ω1∈[30.04，45.90]，Ω2∈[30.25，45.999]，Ω3∈[35.764，50.9]，Ω4∈[37.72，51.362]。Ω1和Ω3水平方向距离为4.42，竖直方向距离为1.54，Ω1和Ω4水平方向距离为4.9，竖直方向距离为3.94，将Ω3和Ω4沿水平和竖直方向向Ω1靠近直至重合，取水平坐标的并集，作出轮廓线，利用2.2的方法求解各参数值如表4所示。

3 测量数据优化修正处理

3.1 關于圆的测量

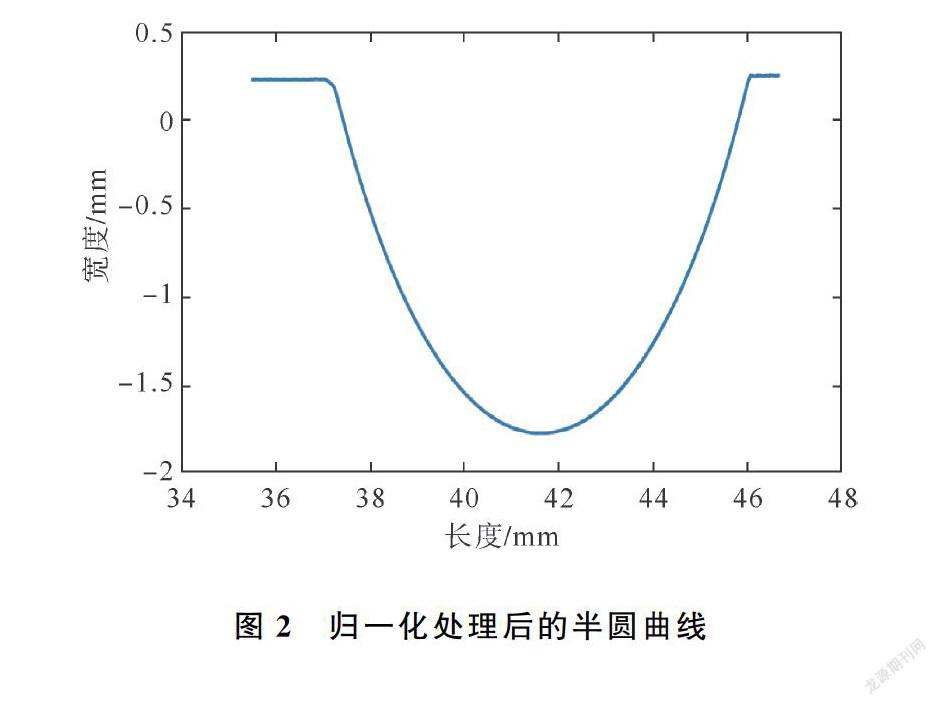
关于圆的测量根据图像显示，去除重合部分，将9组坐标简化为3组，得到这3条轮廓曲线横坐标的交集[34.61，46.92]，由于9次测量每次取点约为6万个，因此等距取6万个点，并对3组曲线使用Matlab分别进插行值sji，i=1，…，80 000，j=1，2，3，令ri，13∑3j=1zji为归一化后的坐标，得到归一化后的曲线，接下来利用坐标旋转公式获得水平坐标。利用2.2的求解方法得到旋转角度arctan 0.158 9，将其旋转后得到归一化半圆曲线的图像，利用2.3相同的求解方法求解各参数值如表5所示。半圆归一化修正后的曲线如图2所示。

3.2 关于角度的测量

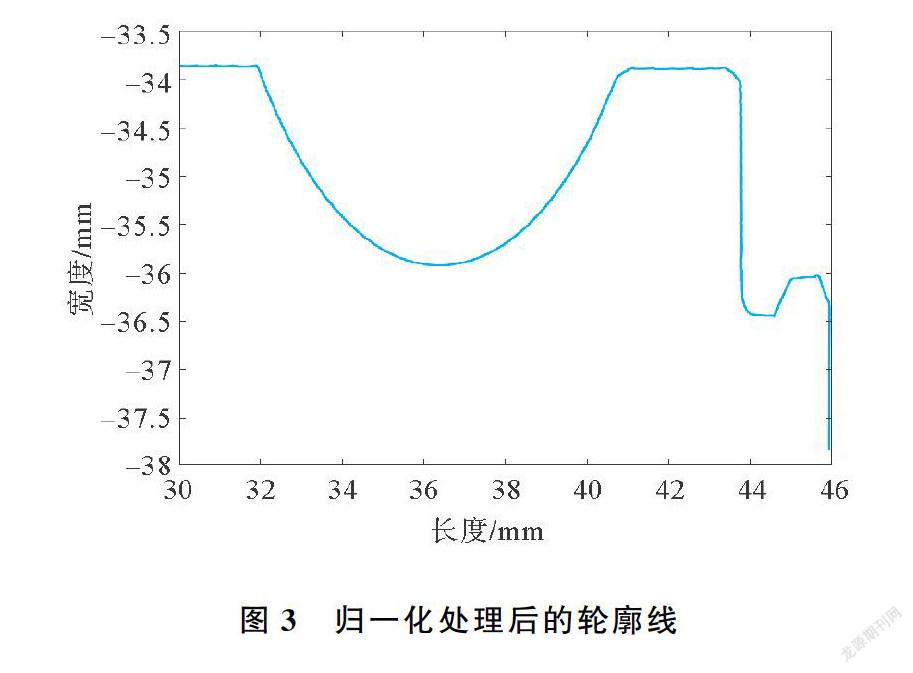
关于角度的测量根据图像显示，去除重合部分，将9组坐标简化为2组，取这2组的数据，得到这2条轮廓曲线横坐标的交集[34.53，47.91]，由于9次测量每次取点约为4万个，因此等距提取4万个点，并对这2组曲线使用Matlab分别进插行值sji，i=1，…，800 00，j=1，2，令ri，12∑2j=1zji为归一化后的坐标，得到归一化后的曲线，求解k=-5.7，θ=π-arctan k=100.3°。归一化曲线如图3所示。

4 结论

通过对接触式轮廓仪测量数据的绘图和分析，利用阈值的思想筛选直线上的点，求解圆弧转折点的坐标。对于由测量物件摆放位置造成的误差，利用旋转后点的坐标公式和回归分析对误差进行修正，得到轮廓线的各项参数值。最后，利用插值法将多次测量的数据进行归一化处理，提高了工件的测量精度和稳定性。本文在求解关键点时运用了回归分析的方法，计算量较大，如果采用数据平滑理论进行求解，可视化效果和计算效率会进一步提高。

参考文献

[1]罗正国.表面结构与粗糙度测量方法浅析[J].工具技术，2006，6（3）：123-125.

[2]尤越，王乔方，字正华，等.一种基于Matlab的非球面光学元件面形参数测试技术[J].红外技术，2014，36（4）：331-335.

[3]郭隐彪，郭江，王振忠，等.非球面检测路径与高精度曲线拟合算法研究[J].中国机械工程，2008，19（10）：1201-1204.

[4]姜启源.数学建模案例精选[M].北京：高等教育出版社，2014.

[5]刘红玉.基于主成分分析和聚类分析的陇南地区特色农业经济分析[J].青岛大学学报（自然科学版），2020，33（4）：140-144.

[6]董田田，董学士，张睿，等.基于指数加权移动平均法的企业销量预测[J].青岛大学学报（自然科学版），2020，33（4）：50-54.

[7]高瑞翔.余弦误差在轮廓仪角度校准中的影响[J].上海计量测试，2015，42（5）：21-22.

[8]贾宁.轮廓仪非球面接触测量的核回归误差补偿算法[J].组合机床与自动化加工技术，2018，8（9）：99-102.

[9]王旭刚，金文胜，刘燕，等.轮廓仪测量双半内圈沟曲率的方法的改进[J].计量与测试技术，2018，45（10）：86-88.

[10] 韩志国，李锁印，冯亚南，等.接触式轮廓仪探针状态检查图形样块的研制[J].微纳电子技术，2019，56（9）：761-765.

[11] WHITEHOUSE D J. Enhancement of instrument and machine capabilites[J]. Nanotechnology， 1996， 7（1）： 47-51.

[12] FORBES G W. Shape specfician for axially symmetric optical surfaces[J]. Optics Express， 2007， 15（8）： 5218-5226.

[13] FORBES G W， BROPHY C P. Asphere，O asphere，how shall we describe tree？[J]. Proceedings of SPIE， 2008， 10（8）： 6200-6221.

[14] FORBES G W. Robust efficient computational methods for axially symmetric optical aspheres[J]. Optics Express， 2010， 18（19）： 19700-19712.

[15] INDRASIS M， INDRANIL G. Thermohydraulic behavior of minichannel surface simulated with gaussian function and actual roughness data generated using three-dimensional optical surface profilomete[J]. Journal of Heat Transfer， 2020， 142（10）：1-11.

Application of Mathematical Modeling in Contour Marking

FENG Ying-hua

（School of Public Education， Huainan Union University， Huainan 232001， China）

Abstract：

The measurement of the contour curve of the workpiece is not accurate because of the problems caused by contamination， defect and inaccurate scanning position when measured by the contact profilometer. Thus， threshold idea is used to get the important parameters of the contour curve， and the data is normalized by the Matlab interpolation. It is shown that the errors caused by scanning probe and object position could be corrected through the mathematical modeling method.

Keywords：

contourgraph; fitting; threshold; interpolation; rotational coordinates