如何引领小学生理解数学概念的“本质属性”

于勇 周奕 杨佳静

数学概念是客观现实中的数量关系和空间形式的本质属性在人脑中的反映，正确掌握数学概念是小学生学习数学知识的基石，更是培养小学生数学素养和思维能力的前提。因此，概念教学是小学数学探讨中的一个重点板块，帮助小学生正确理解和运用数学概念。

一、巧妙变式，突出概念的本质属性

所谓变式，就是所提供的实例或材料要不断地变换呈现形式，改变非本质属性，使本质属性恒在，由此初步形成概念。巧用变式进行概念教学，不仅有利于激发学生学习数学的兴趣，有利于学生形成清晰的概念，更有利于学生开发思维，让学生真正理解和掌握概念。如，教学“用百分数解决问题”中的“发芽率”概念时，首先引导学生在完成例题（表一）的基础上，初步理解“发芽率”的内涵;然后，对例题进行如下变式（表二---表三），引导学生深入理解概念;最后，引导学生通过对例题与变式题的对比分析，使学生认识到“发芽率”的本质属性，真正掌握该概念。

二、反面衬托，强化概念的本质属性

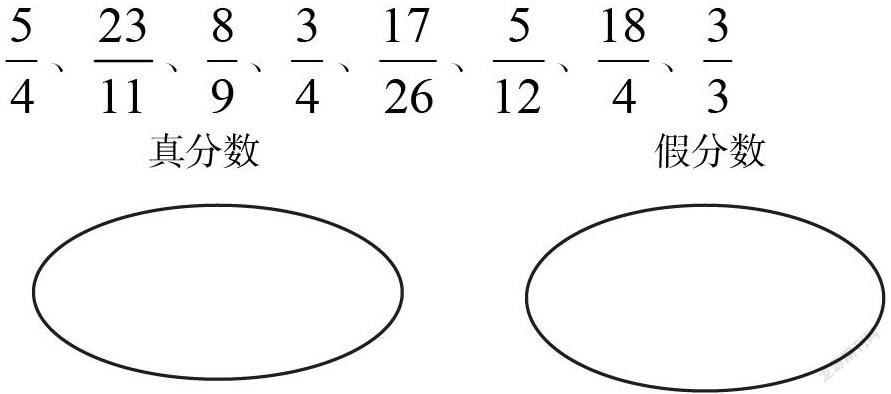
反面衬托是利用与所教学概念相矛盾或相反的数学知识、数学模型，进行与所教学概念的对比分析，进一步掌握数学概念的方法，从正反两个方面进行概念教学。例如，假分数的定义是“分子比分母大或分子和分母相等的分数叫假分数。假分数大于1或等于1。”在该定义中要注意两点：一是分子与分母的大小关系;二是分数与1的关系。这两点都是判断一个分数是否是假分数的充分依据。为使学生进一步理解这个概念，除正面揭示外，还可以利用真分数的概念进行反面衬托，让学生辨别正误，确切地掌握假分数的概念。如，下面的分数哪些是真分数，哪些是假分数？

三、准确描述，概括概念的本质属性

教学数学概念时，要引导学生通过多层次的概括，用简练的语言把概念的本质属性固定下来，以利于学生对概念的理解、巩固、运用。首先，描述时机要恰当。对概念进行描述能起到组织、巩固、整理知识的作用，要引导学生通过自己的观察、比较、分析、综合等手段概括概念的本质属性，并用清晰简洁的语言进行描述，然后下定义。下定义时机要恰当，在学生还没有真正理解概念内涵之前就下定义，容易导致对概念的死记硬背;同样，下定义过迟也不利于对概念的掌握，甚至阻碍学生对概念的内化。其次，下定义的文字要准确。下定义是对概念的本质属性作出准确的概括，定义中关键词语一定准确无误。如：梯形的定义“只有一组对边平行的四边形，叫梯形。”，这里的“只有”、“一组”等是该定义中的关键词语，更改任意一个都是错误的，“一组对边平行的四边形，叫梯形。”或“只有对边平行的四边形，叫梯形。”的说法就是典型错例。最后，下定义要有一个过程。小学数学概念是最基本的、是初级的、是有待发展的。例如：小学中角的定义“有一个点引出两条射线所组成的圖形。”这种定义使小学生很难理解平角，尤其是周角也是角。到了中学，角的定义是“射线环绕它的端点旋转的旋转量”，同时也出现720°、5400°等角。由此可见，对概念下定义要有阶段性，要符合小学生的认识水平和认识特点，表述要由低到高，逐步要求。

四、自举实例，加深概念的本质属性

自举实例就是要求学生把已经初步获得的概念简单应用于实际，通过生活中的具体实例来说明概念，加深对概念的理解。教学时，教师可根据小学生对概念的认识带有具体性特点，在学生通过分析、综合、抽象、概括出具体概念后，引导他们自举实例，把概念具体化。如，教学“进一法”概念时，在抽象、概括之后，可放手学生结合自己的生活阅历，举出一些用“进一法”取近似值的实例。如：王老师组织六年级35名学生去公园划船，若一条船最多可载6人，至少要租几条船？这样教学，不仅符合学生具体---抽象---具体的认识规律，还可使学生更准确地把握概念的内涵和外延。

五、灵活对比，辨析概念的本质属性

小学数学中的很多概念是相近的，是有着一定区别和联系的。如：数位、位数、计数单位，方程与等式等。教学时，教师要引导学生，及时和邻近概念、易混概念进行比较，弄清它们之间的区别与联系。如：用表格法对质数、质因数、互质数的比较（表四）。

总之，小学生数学概念的建立不是一蹴而就的，而是数学知识体系建立中的一个复杂活动。教学时，教师要根据小学生的认知特点，在实践中理解、深化、运用概念，逐步形成概念的认知体系，在学生掌握概念的同时，发展学生学习数学的能力。

（江苏省苏州市吴江区思贤实验小学 江苏苏州 215200）