新高考中数学文化试题赏析

李小东

摘 要：我国普通高中教育改革在不断深入，新课程标准下对学生的文化素质培养也有了新的要求，这体现在新课标改革下的高考试题当中，而数学文化试题则在全国高考卷试题中经常涉及，对于此类数学文化类试题作赏析有助于让学生更好地了解中华传统文化的光辉历史，从而增强民族自信心。了解我国数学研究历史的来龙去脉，对数学思维培养、应用能力提升、文化修养提升等方面都有很好的促进作用，同时也能把数学理论与日常生活相结合，突出数学教学的社会性。

关键词：数学文化;试题赏析;教学思考

引言：2017年颁布的《普通高中数学课程标准》将数学文化定义为数学领域内涵盖的思想、方法、表达形式、思维方式和长期丰富发展的历史，以及数学在人类社会发展进程中对科学技术、日常生活、文化体育方面的重要推动作用。新课标要求教师在教学当中应当将数学文化融入到课程学习中，引领学生更好了解其进步历程、感受数学的关键作用，激发其学习兴趣，增强学科素养，高考中对数学史、思维逻辑以及生活应用方面都有所考查，学生应重点掌握。

一、以数学发展史为背景高考题目赏析

这类题目是以各类数学发展历史中的事件和人物为背景，将前人在不同领域研究的杰出数学成果结论，经过适当的转化变形后编制成选择题、填空题或者简答题，多以代数和几何两种题型出现，题目的范围也较广，涵盖了古今中外，比如欧几里得发现的重要定理、杨辉三角、秦九韶算式等等，一方面是考核学生是否能够从表面的历史事实中看到题目真正的本质是检测的哪一部分的知识点，另一方面则是让学生解题的过程中多了解和感受数学悠久的历史文化，其应用意义和文化理念，受到数学文化环境熏陶，从而提升其学习探究数学的兴趣程度[1]。

以算法的灵活应用为例来对2016年的全国Ⅱ卷文科试卷中的9题为原型中的数学文化元素进行分析鉴赏。

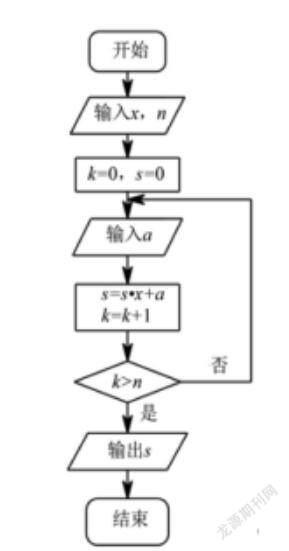
例题1.在中国古代一种用于多项式计算的方法较为有名，称之为秦九韶算法，它的整体计算过程如图一所示，先按照改图的程序将一组数值x，n代入运算程序后，最终得到运算值a和b，若设x=2，n=1，相应的图框中输入的a分别是2、2、5，那么最终的输出的s的值是（ ）

A.7 B.12 C.17 D.34

思路分析与题目赏析：题目中提到的“秦九韶算法”其历史较为悠久，是南宋时代一位著名的数学家秦九韶在多项式运算中研究出的一种较为简便的运算方法，它的基本思路是把一个一元高次的多项式转换成多个一次等式的，次幂数和等式个数相等，这种方法能够极大地减少计算的过程，简化运算复杂程度。在当代运用计算机二进制计算多项式时，经过大量实践证明，我国的该种方法依然是最为优秀的方法之一，它可以大大减少计算机中央处理器的运算频次，加快计算速度，此法在国际也被称之为霍纳算法，用英国数学家霍纳来命名的。

对该题而言，要透过现象看到题目的本质，考查基本的程序性计算问题，要对于是否两种情况做出准确判断，最后退出s的值，容易得出s=17，选C。

中国传统数学历史为背景设置题目更为深远的意义则是能够增强的学生的民族自豪感和爱国主义情怀，显然这种情怀的培育和增强不是像历史题、政治题等可以直观鲜明的体现的，其特别之处在于将中外两种数学思想在其交汇点上做了全面深入的对比，让学生在中外不同的数学思维的试验和对比中，找到中华民族的优秀品质所在，中国的传统思维并不是全部由于国外的数学方法，但是其理论成果都是原创性的，也较好的指导的社会发展，这才是数学文化的魅力所在，它不是为名利而生，而是为民族的利益价值而生。

以2015年全国Ⅱ卷卷中的第8题为例，题目的表述是程序框图（可参见图一）的运算思路是来源于我国古代数学中的“更相减损术”按照该程序框图的预算程序，当输入x、y分别为14，18，则得到的值是（ ）。

这题的本质是解决两个数之间的最大公约数的问题，我国的数学家探究出“更相减损术”能够有效简便地解决同类的相关问题，当然，国外的数学家也对这种问题做了探究，提出了对应的程序算法，被称之为欧幾里得算法，它是按部就班的代入相应的值通过寻找公约数来求出答案。把中外两种运算过程和简便程度做一详细对比后发现，我国的该方法在运算步骤、运算时间上都略胜一筹，也是符合现代计算原理的一种方法，在这一方向上占据了领先的位置，学生可以通过对此段历史的了解增进爱国之情，更激发了努力学习，为国家民族再添新砖的热情[2]。

二、数学指导人类进步为背景的高考数学题类赏析

数学的美妙之处不仅在于其严密的逻辑性和广阔的未知性与创新性，更在于它对实际生产生活的重要指导作用，传统历史上的数学研究多是人类在长期社会实践中积累的经验，其成果也是用来帮助人们解决现实中遇到的社会生产问题，比如生产中的投入量产出量，成本效益问题，建筑中的几何问题，生活中的分配、交换问题等，这些问题衍生出了相应的数学成果，长时间的成果积累和不断传承创新，最后沉淀形成了博大精深的数学思维和历史文化，无论在历史长河中的人和还是当下的人类，都要借助数学这一神秘而又亲切的伙伴来认识世界、改造世界、与世界实现和谐相处，这也体现出数学“以数理造化人类”的高远境界。

以2015年全国一卷中的一道数学题为范本来对这一独特数学文化体现做一鉴赏和分析。

例题2.作为我国历史上数学发展里程碑式的重要学术成果，《九章算术》中涵盖了丰富的数学知识和数学公理，直至现在仍有较多在被沿用和发展。该书中就曾提出问题：

用当前的白话文翻译过来就是，以房屋内部的墙角根处放置了一堆谷子（米），这对谷子的形状是一个圆锥体削掉四分之三后的形态，谷堆圆锥底部的弧长是八尺（古代的一种计量单位），谷堆的高度是五尺，求该谷堆的占用体积是多大，且一共堆放了多少粒的谷米，题目中也告知了一斛米的体积约为1.6立方尺，设圆周率π=3，则可以计算出谷堆斛中方的谷米大约有多少，

题目鉴赏：此题目的考查背景就是来源于古代人民的生产生活实际，古代的谷物储藏无论是官宦市民都是一件大事，如何利用有限的空间存储更多的粮食，计算一定空间内储藏谷物的数量都是管理者和所有者需要掌握的技能，而这就涉及到规则物体的一些几何知识，此题就是从这个背景出发即让学生了解了《九章算术》的一些历史渊源与内容知识，还考查了圆锥等立体几何知识，实现了两者的有机结合，与生活融合的题目，能够让学生从枯燥乏味抽象的各类数字公式中脱离出来，进入到实际生活中，以问题为导向来理解数学的精妙之处[3]，从而潜移默化间将数学文化的优秀品质传输到学生之中，把数学思想根植到我国古代的优秀传统文化当中，从题目的解答可以解决实际社会问题，也学生有了一定的成就感，对数学这门学科的现实意义有了更加直观深入的了解，也培养了学生的学习积极性和主动性，真正体现了“以数化人”文化境界。

三、以培育数理思维与逻辑分析为背景的高考题目赏析

数学文化的内涵极为丰富，学习领悟文化内涵要内化于心，外化于形，要认识到数学文化的外在表现上是悠久的历史积累，各类数学原理和概念，对应的运算规则、公式等实实在在的要素，其更为关键的是看不见的逻辑分析、数学方法、数学审美、数理思维等等无形的观念意识，它才是整个数学文化的内在核心，而学习研究数学的高层次境界就是脑海中忘却了有形的公式理论，留下了应对各类问题的理念和方法，能够以不变应万变，把这种无形的元素贯穿于整个数学问题的思考分析、逻辑判断和创新上[4]。下面以2017年全国Ⅱ卷理科第7题为原型的题目来做一赏析。

例3.A、B、C、D四位学生去向老师查询数学竞赛的成绩，老师暗示，你们四人中有2位优异，2位良好，我现在让A看B、C的成绩，让B看C的成绩，给D看A的成绩。最后A对大家说：我还是不知道我的成绩，根据以上信息，可推断（ ）

A.B可以知道四人的成绩

B.D可能知道四人的成绩

C.B、D可以知道对方的成绩

D.B、D可以知道自己的成绩

题目的鉴赏和分析：此题重点在考查学生的逻辑推理能力和内容的梳理能力[5]，是提升其逻辑思维素養的有效方式。解题思路简述，根据题目的内容可知，当A看成绩后对其他人说到他仍不知道自己的成绩，这就可以较为明显地判断出四人中B、D二人中定有一人成绩为优异、另外一个人是良好，在结合题目给出的限定条件，这四个人中有2位是优异，其余2位是良好，因此在B看到了C的成绩后，如果C自己是优异，那么B就是良好，如果C是良好，那么B就是优异，二者必有其一，因此B定知道自己的成绩，同理可知，在D看到了A的成绩后，如果A的成绩是优异，D则应当是良好，如果A成绩是良好，则D的成绩就是优秀，综上可易得出D选项表述正确[6]。

结束语

不仅是数学科目，其他各个学科都有其自身的发展规律和独特的文化渊源，而数学文化则是与生活更为贴近，它反映着这个学科的发展内在机理和特有本质，而高考题目中融入了数学文化元素，正是新课标中对学生文化素养培育目标的生动实践，数学对于推动人类文明进步的重要意义不言而喻，而我国当前在数学等基础学科领域研究方面还存在较大的差距，因此从高考这个节点入手，就着重培养准大学生的数学素养，弘扬数学文化，为后续高层次的数学人才建设打下良好的基础。

参考文献

[1]中华人民共和国教育部制定.普通高中数学课程标准（2017年版）[S].北京：人民教育出版社

[2]张文卓.现代化高中数学数学文化的发展[J]，中国现代化教育论坛，2015（12）.

[3]张洪山.基于现代化教学中数学文化的弘扬与发展[J]，高中数学文化教育论述，2013（32）.

[4]郭文芳.数学文化在近几年高考试题中的渗透与赏析[J]，数学文化的渗透与赏析，2016（09）.

[5]李汝雁、郭要红.2018年高考数学文化试题的评析与教学建议[J].数学通报，2018（09）：31-33-61.

[6]左武明、吕喜文.高考试题中古数学元素对数学文化传播效果赏析——由一道高考题谈数学文化[J].中文信息，2019（06）：220-298.

本文系“甘肃省教育科学‘十三五’规划2019年度课题，课题名称：基于高考背景下数学文化渗透的教学策略研究，课题立项号：GS[2019]GHB1008”研究成果。