含凹坑缺陷管道环焊缝应力有限元分析

储玲玉 刘觉非 苏林 毛瑞麒 徐杰 鲍庆河 李鑫

摘要：基于有限元方法，采用ABAQUS有限元仿真模拟软件，参考实际管道环焊缝的坡口形状和热影响区材料的软化现象，建立了含凹坑缺陷管道环焊缝非线性有限元分析模型，对不同载荷作用下的含凹坑缺陷管道环焊缝进行应力分析，探讨了凹坑尺寸、焊缝余高以及热影响区材料属性等因素对应力分布的影响规律。结果表明：凹坑周边发生明显的应力集中，凹坑深度对管道极限承载力影响显著，随着凹坑深度的增加，腐蚀管道的最大等效应力显著增大，且峰值应力集中在焊缝区;腐蚀管道在极端拉伸载荷作用时，焊缝余高内凹坑缺陷的最大等效应力集中在热影响区;凹坑深度大于余高时，最大等效应力位于焊缝中心的凹坑边缘。

关键词：管道环焊缝;凹坑缺陷;焊缝余高;有限元分析;安全评估

中图分类号：TE88      文献标志码：A         文章编号：1001-2003（2021）04-0008-06

DOI：10.7512/j.issn.1001-2303.2021.04.02

0    前言

我国高速发展的经济对油气资源的需求不断增加，各种油气工程建设项目随之逐渐增多、油气管网里程的逐年增加[1]。管道运输业快速发展的同时，为了保障石油、天然气等管道长距离运输的安全，需要定期对管道进行无损检测和安全评估[2-3]。凹坑是管道环焊缝常见的体积型缺陷，不仅会减小管道环焊缝的实际截面面积，还会引发材料剩余强度下降，引起局部应力集中，削弱管道环焊缝的抗变形能力[4-8]。因此，分析腐蚀缺陷对管道环焊缝结构应力状态的影响至关重要[9-11]。

根据实际管道环焊缝坡口形状和热影响区材料的软化现象，建立了含腐蚀凹坑缺陷的管道环焊缝非线性三维有限元模型，探讨了不同载荷作用下管道焊缝凹坑大小、焊缝余高以及热影响区材料属性等因素对缺陷管道环焊缝应力分布的影响规律。

1 管道环焊缝有限元模型

1.1 几何模型

X60钢相当于国内L415钢，多用于输送石油、天然气等的大口径焊接钢管，其屈服强度高、塑性好，可承受较高输送压力，在我国现役管线钢应用中占有一定比重。管道外径为529 mm，壁厚9 mm，管道结构几何模型如图1所示。考虑管道的结构对称性，仅取1/4模型进行有限元建模与计算分析。根据实际管道坡口形式建立的含凹坑缺陷管道环焊缝的三维几何模型如图2所示，管道环焊缝由管道母材区、焊缝区和焊接热影响区三部分组成。同时，模型中考虑了焊缝表面余高的影响。为了便于建模与比较分析，本研究将凹坑形状近似为规则的矩形，凹坑中心位于管道环焊缝中心（见图2），考虑了凹坑大小及深度的影响。

1.2 材料属性

X60管线钢屈服强度为415 MPa。一般情况下，管道焊接时焊缝强度高于母材，考虑到热影响区的软化现象，为便于比较分析，同时参考以往研究，取焊缝区材料强度比母材区高10%，热影响区材料强度比母材区低10%。考虑到材料非线性，为反映管道材料屈服后的硬化行为，在材料模型中采用Ramberg-Osgood幂硬化应力-应变法则，其表达式为：

式中 ε0为初始应变，ε0=σs/E;σs为屈服应力（单位：MPa）;E为弹性模量（单位：MPa）;α为屈服偏移;n为硬化指数。X60管线钢焊材、母材以及热影响区的流动应力与等效塑性应变的关系曲线如图3所示。

1.3 网格划分

采用ABAQUS软件进行有限元建模，采用八节点六面体单元对模型进行网格划分。考虑凹坑周围应力梯度变化较大，划分时对焊缝中心凹坑周边网格进行细化，使其尽可能均匀致密;远离焊缝中心区域的网格采用逐渐发散的方式。管道整体及焊缝局部的有限元网格如图4所示。

2 载荷条件

管道在运行过程中所受的载荷状况复杂。首先，考虑到设计压力是管道工作中所允许承受的最大工作压力，故将管道的设计压力定为基础载荷。根据管道设计规范GB 50251-2015，可推出管道设计压力的计算公式为：

式中 P为设计压力（单位：MPa）;D为管子外径（单位：mm）;σs为钢管规定的最小屈服强度（单位：MPa）;φ为焊缝系数，按照规范，此处取值1.0;δ为管道计算壁厚（单位：mm）;F为强度设计系数，按照GB50251标准，此处管道强度设计系数取0.72;T为温度折减系数，当温度小于120 ℃时，T值应取1.0。由式（2）计算出管道设计压力为10 MPa，即管道加载的基础载荷为10 MPa。

管道在实际运行过程当中处于两向应力状态，内压使得管道环向产生拉伸应力，而轴向既存在压缩应力也存在拉伸应力的情况。参考文献[12]中，对缺陷管道环焊缝设置极端载荷条件，分别有三种情况：①基础载荷极限（即设计压力10 MPa）;②极端压缩载荷：基础载荷与0.18σs轴向压缩应力的叠加;③极端拉伸载荷：基础载荷与0.9σs轴向拉伸应力的叠加。

3 结果分析与讨论

3.1 含凹坑缺陷管道环焊缝的应力分析

根據基础载荷、极端压缩和极端拉伸载荷条件，分别对环焊缝存在凹坑缺陷的管道进行有限元模拟计算。取矩形凹坑边长为6 mm，沿壁厚深度为30%t，三种载荷条件下凹坑周围的von Mises等效应力云图如图5所示。

由图5可知，凹坑边缘区域的应力明显增大，但影响范围仅在凹坑周围较小的范围内，管体部分的应力场分布均匀。对比三种载荷条件下的管道等效应力云图，在管道基础内压作用下，管道发生变形向外膨胀。管道在基础载荷和轴向压缩载荷组合作用时，与基础载荷的应力场分布相似，管体发生膨胀，最大等效应力较基础载荷有小幅增长。管道在基础载荷和轴向拉应力的叠加载荷作用下，管道整体被拉长，应力仍集中在凹坑附近区域。

3.2 凹坑尺寸的影响

针对矩形凹坑的大小（矩形边长）和其沿壁厚深度不同的情况分别进行比较分析。取矩形凹坑边长分别为6 mm、10 mm、13.6 mm（焊缝宽）、16 mm（跨焊缝），深度分别为10%t～50%t（t为管道壁厚，单位：mm）的壁厚。

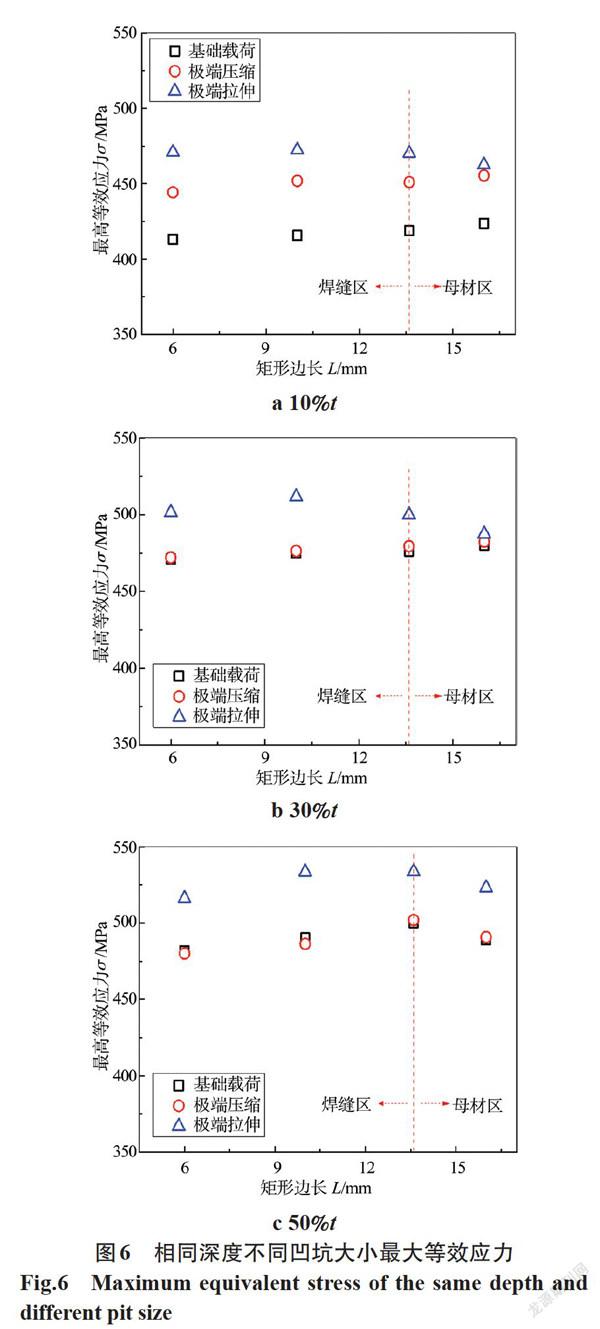
图6为不同凹坑大小（涵盖了焊缝中心到跨焊缝和母材的情况），深度分别为10%t、30%t和50%t（涵盖了浅凹坑和深凹坑的情况）时的结果。

由图6可知，当凹坑大小及深度不同时，极端拉伸载荷作用下管道的最大等效应力明显高于基础载荷和极端弯曲载荷下的情况。对于本研究中考虑的最浅的凹坑（见图6a），在相同深度下，凹坑大小对管道分别在三种载荷作用下的最大等效应力影响不明显。随着凹坑深度的增加（见图6b、6c），对位于焊缝区的凹坑（6 mm→13.6 mm），随着其尺寸增大，三种载荷作用下管道的最大等效应力略有增加。当凹坑位于跨焊缝和母材区时（如边长达16 mm的凹坑），在拉伸应力作用下的最大等效应力相较焊缝区凹坑呈一定的下降趋势。由应力分布云图可知，跨焊缝和母材的凹坑，其最大等效应力集中在热影响区，而由于热影响区的软化现象，该处的材料强度低于焊缝和母材，导致其应力水平下降。

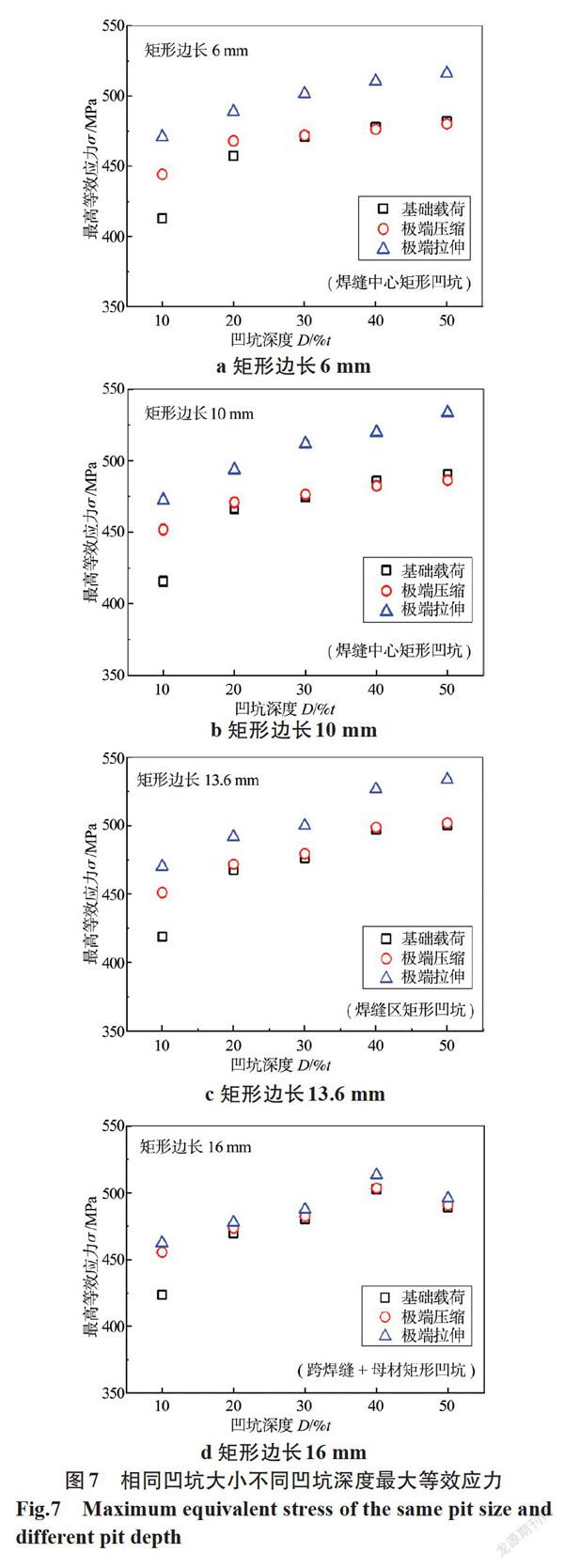
相同凹坑大小在不同凹坑深度下管道的最大等效应力分布如图7所示。

由图7可知，焊缝处凹坑深度对管道应力具有显著影响。对位于焊缝区的凹坑（凹坑边长为6 mm→13.6 mm），随其深度的增加，最大等效应力单调增大，即凹坑越深，管道的剩余强度越小，越容易发生失效。当凹坑位于跨焊缝和母材时，随着深度（10%t→40%t）增加，最大等效应力增大，当凹坑深度达到50%t时，三种载荷下的应力水平均有一定的降低。

3.3 焊缝余高对凹坑缺陷管道环焊缝应力分布的影响

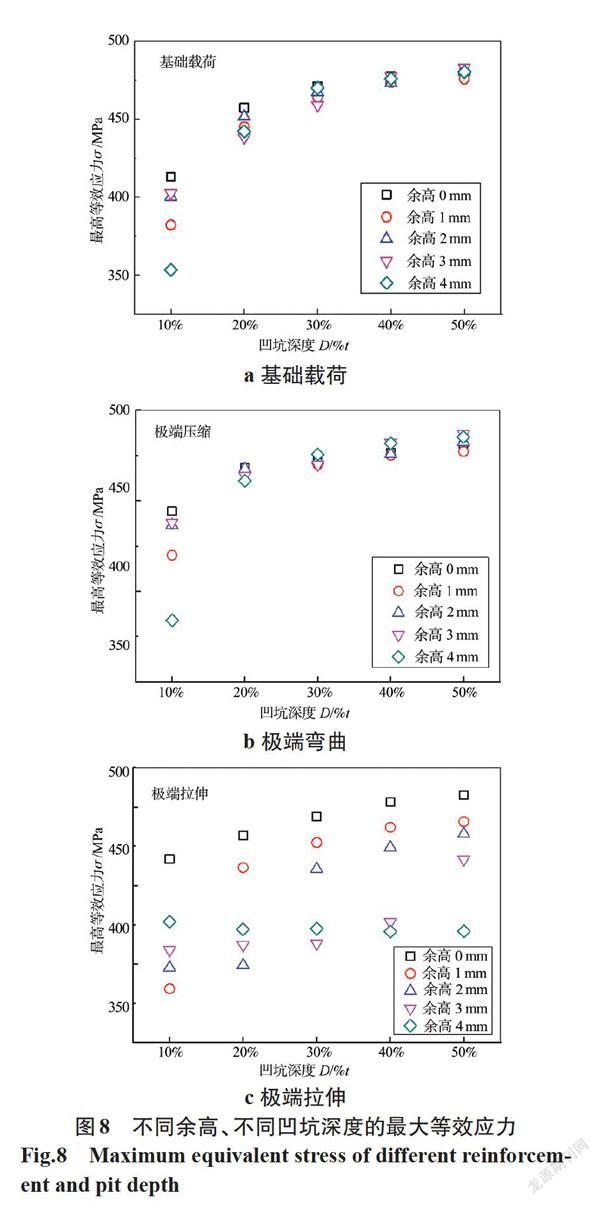
管道焊接时，焊缝表面会存在一定的余高（即超出焊缝表面焊趾连线上面的那部分焊缝金属的高度），不同标准根据焊缝级别不同对余高值有不同的要求，但一般不超过4 mm。为了研究余高大小对管道环焊缝应力的影响，取余高分别为1 mm、2 mm、3 mm和4 mm，凹坑大小为6 mm，深度分别考虑浅凹坑和深凹坑（即10%t～50%t），在三种载荷条件下进行有限元模拟计算，同时与没有余高的情况进行对比，结果如图8所示。

由图8可知，不同深度凹坑在三种载荷作用下，有余高的焊缝（余高为1～4 mm）相比没有余高时（余高为0）其最大等效应力均有不同程度的降低。可见，焊缝余高在一定程度上使焊缝的横截面增加，承载能力提高。

在基础载荷和极端压缩载荷作用下，余高对浅凹坑（10%t）的影响比较明显，对深凹坑的影响较小，且在这两种载荷作用下的最大等效应力均位于焊缝中心的凹坑边缘。

而当管道处于极端拉伸载荷作用时（见图8c），不同凹坑深度下余高均有明显影响，并且由计算结果可知，最大等效应力的位置与凹坑深度有关。当凹坑深度小于余高（即缺陷位于余高内）时，最大等效应力位置转移到热影响区，如图9所示;凹坑深度大于余高时，最大等效效应力仍位于焊缝中心的凹坑边缘。

另外，由图8结果可知，在本研究的余高值范围内（1～4 mm），不同深度凹坑的最大等效应力并非随余高增大单调减小的。即余高的存在虽然一定程度上增加了焊缝横截面，提高了承载力，但其值并非愈大越好，余高愈大，焊趾位置的应力集中程度愈明显，焊接接头的强度反而会降低。另外，余高过大，会使拉伸载荷下最大等效应力的位置转移到热影响区，而焊接热影响区软化往往也是环焊缝失效的主要原因之一。因此，在实际焊接过程中考虑余高补强的同时，还需根据实际结构合理控制余高值。

3.4 热影响区材料的影响分析

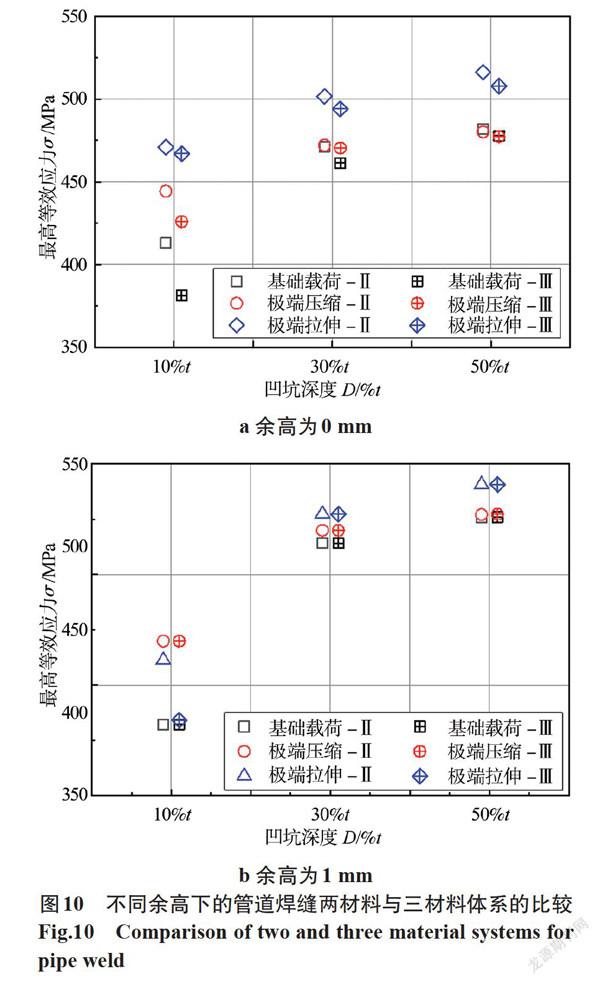
考虑由试验测量来获得热影响区的材料属性较为困难，因此为简化模型，很多研究者选择简化的材料模型体系，如仅设置母材和焊材的材料属性，而忽略热影响区的影响。为了比较分析这种材料简化对结果的影响，文中针对两种材料体系（Ⅱ：焊材+母材，Ⅲ：焊材+母材+热影响区）分别进行了对比分析，不考虑焊缝余高（余高为0）和有余高（1 mm）时，深度分别为10%t、30%t、50%t的凹坑在三种载荷条件下的结果如图10所示。

由图10可知，不考虑余高时，Ⅲ材料体系的结果均略低于其相应的Ⅱ材料体系，且浅凹坑更为明显（见图10a）。当考虑焊缝余高时（见图10b），两种材料模型体系对结果的影响较小。

4 结论

采用有限元方法，运用ABAQUS软件建立了含凹坑缺陷的X60管道环焊缝的非线性有限元模型，探讨了凹坑大小及深度、焊缝余高以及焊缝材料模型等对管道环焊缝应力分布的影响，结果表明：

（1）管道环焊缝凹坑缺陷周围产生明显的应力集中，相同凹坑尺寸时，相比极端压缩和基础内压载荷条件，极限拉伸载荷下的管道应力最大。

（2）焊缝处凹坑沿壁厚深度大小对应力分布影响显著，随凹坑深度增加，管道最大等效应力明显增大;凹坑深度相同时，凹坑大小对应力影响较小。

（3）焊缝余高在一定范围内可使管道的最大等效应力降低，但余高过高时会导致焊趾部位应力集中;应力峰值位置与凹坑深度有关，当凹坑深度小于余高时（即缺陷位于余高内），最大等效应力位于热影响区;当凹坑深度大于余高时，最大等效应力位于焊缝中心的凹坑边缘。

（4）焊缝材料体系中考虑热影响区材料属性（不考虑余高）对结果有一定影响，且浅凹坑较为明显;当考虑余高时，这种影响变小。

参考文献：

隋永莉. 油气管道环焊缝焊接技术现状及发展趋势[J]. 电焊机，2020，50（9）：53-59.

戴光，郑克耀，杨志军，等. 管道外自动漏磁检测技术及试验[J]. 无损检测，2017，39（7）：18-22，45.

戴光，吴忠义，朱祥军，等. 管道内外壁缺陷的漏磁检测[J]. 无损检测，2018，40（3）：19-23，28.

王战辉，马向荣，党睿，等，含矩形腐蚀缺陷管道剩余强度的有限元分析[J]. 当代化工，2020，49（8）：1715-1718.

帅健，王旭，张银辉，等.高钢级管道环焊缝主要特征及安全性评价[J]. 油气储运，2020，39（6）：623-631.

杨辉，王富祥，陈健，等.基于应变的管道环焊缝表面裂纹有限元分析[J]. 石油机械，2017，45（3）：114-117.

李根，张腾.几种焊接缺陷对X70管道环缝接头应力集中的影响[J]. 焊管，2014（6）：48-52.

金晶.含裂纹、气孔及多次重熔焊缝的焊接接头疲劳性能研究[J].电焊机，2015，45（1）：89-94.

王旭，帅健.输气管道环焊缝表面裂纹管道极限载荷计算方法[J]. 天然气工业，2019，39（3）：94-101.

沙胜义. 输油管道环焊缝缺陷疲勞寿命评估[J].管道技术与设备，2017（2）：28-31.

韩志成，丁红胜，姚登樽，等. 基于应力设计的管道环焊缝缺陷评估[J]. 焊管，2016，39（8）：23-26.

李燕，帅健，隋永莉，等. 含气孔缺陷的管道环焊缝应力分布[J]. 石油科学通报，2016（3）：417-424.

收稿日期：2021-01-14

基金项目：国家自然科学基金资助项目（51301197）;江苏省自然科学基金资助项目（BK20130182）;中国石油化工股份有限公司资助项

目（318019-2）;国家重点研发项目（2018YFB2001204）;大学生创新训练项目（202010290125Y）

作者简介：储玲玉（1995—），女，硕士研究生，主要从事管线钢结构完整性评估和有限元数值模拟的研究。E-mail：j.xu@cumt.edu.cn。