一题一课，发现知识本质

何佳丹

一、缘起：基于教材习题，深入解读素材

人教版六年级下册在学习完圆柱体积以后，教材上有这样一道练习题（图1）。这是一道难度较大的练习，具有很强的思维性与探索性。一题变一课，笔者尝试通过这一学习材料，设计一节拓展课，引导学生展开深度学习，分析长方形与卷成的圆柱体积大小之间的联系，发现规律并理解其背后的原因。如此，既拓展数学的知识面，开阔学生的眼界;又积累数学学习的经验，发展学生的思维。

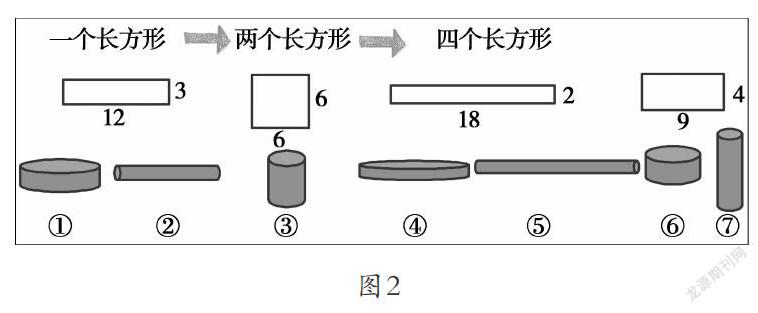
15. 下面4个图形的面积都是36 dm2。用这些图形分别卷成圆柱，哪个圆柱的体积最小？哪个圆柱的体积最大？你有什么发现？（单位：dm）

二、思考：基于学生本位——合理设计教学

（一）把脉现实学情

在六下“圆柱与圆锥”单元的学习中，学生了解了圆柱的基本结构，知道平面图形可以通过平移、卷、旋转等动态变化得到圆柱，理解并掌握了圆柱表面积、体积公式，能解决简单的圆柱体积问题。

习题（图1）内容多，思维含量大，情况较为复杂，4种长方形一共能卷成7种圆柱。笔者对66个学生第一次独立完成练习的情况进行了调研，发现大部分学生会选择通过计算比较圆柱的体积来解决这个问题，再通过数据分析发现规律。但圆柱数量多，计算量大，费时且容易混淆。即使在各个课时中已经较好地掌握了对应的知识内容，但当多个知识交叉综合运用时，学生却不一定能够将这些零散的知识结构在自己的头脑中勾连成完整的认知结构网。从学生的解题情况中可以窥见，不少学生对长方形和圆柱的认知状态是单一的、静态的、割裂的，缺乏动态、整体联结的建构。有的学生对图形运动变化前后的各部分联系的认知是模糊的，误以为长方形的长和宽就是卷成圆柱后的半径和高;有的学生能够辨析清楚长方形的长、宽分别作为圆柱的底面周长和高，却在计算时不能正确应用体积公式。此外，学生的认知结构存在缺口，部分学生没有意识到同一个长方形能卷成两种圆柱（正方形除外）。

（二）精准定位目标

对于长方形卷成圆柱这道题学生究竟该学些什么？这题仅仅会做会算就够了吗？教学更应关注的是学生是否真的内化了解决问题的过程，知识与知识之间能否有效串联？对于表象背后的本质，学生内心充满疑惑，怎样才能让学生探索发现并深刻理解内在规律呢？基于以上思考，笔者设置拓展课教学目标：（1）经历想象、猜想、验证、发现等过程，探究面积相同的多个长方形中，怎样卷成的圆柱体积最大和最小。（2）在操作探究、动手实践、体验活动中参与知识的生成、发展过程，主动地发现知识，体会、了解数学知识的来龙去脉。（3）在解决问题“谁的体积最大”的过程中，通过不同角度的思考和探究，感受策略多样化，发展主动解决问题的能力，积累数学学习经验，拓宽思维场域。

三、践行：活用习题，有序推进

笔者将这道复杂的习题进行解构和重组，借助问题串，分两个阶段循序渐进地引导学生对“谁的体积大”这一问题进行深度探究。

阶段一：问题驱动，层层深入。

1. 猜想验证，唤醒认知。

把一张长方形纸（12 cm×3 cm）卷成圆柱，可以怎么卷？怎样卷得到的圆柱体积更大？请你猜一猜，并验证自己的猜想。

2. 触类旁通，迁移运用。

再给一张正方形纸（6 cm×6 cm），也把它卷成圆柱，比较得到的圆柱体积和刚才两个圆柱体积大小，谁的体积最大？谁的体积最小呢？

3. 溯本求源，发现本质。

再增加两个长方形（18 cm×2 cm和9 cm×4 cm），这四个图形中怎样卷得到的圆柱体积最大？怎样卷体积最小呢？你有什么发现？你知道背后的原因吗？

策略1：具体计算比较。（略）

策略2：字母公式推理。

将长方形的长（a）卷起来作为底面周长，圆柱的体积V=πr2h=。同理，将长方形的宽（b）卷起来作为底面周长，圆柱的体积V=πr2h=。根据长方形的面积相同，可知ab相同，因为a>b，所以，即以最长的边为底面周长卷起来的圆柱体积最大，以最短的边为底面周长卷成的圆柱体积最小。

先从一个图形入手，引导学生厘清长方形与卷成的圆柱各部分之间的联系。学生通过独立思考，经历观察、猜想、验证，初步感知同一个长方形以不同边为底面周长卷成的圆柱体积的大小是不同的。继续增加一个和长方形面积相同的正方形纸卷成圆柱。学生尝试自己推理这个圆柱的体积情况，迁移应用上一环节的知识和学习经验，判斷出圆柱体积的范围，并通过计算准确比较三个圆柱的体积大小。最后再增加两个长方形，完整呈现习题，通过分组合作、组内探讨、全班交流，逐步补充和完善结论。学习中出现了具体计算和字母公式推理两种策略，教师引导学生对两种策略进行沟通整理，感受到两种策略的不同价值取向。即通过计算可以解决问题并发现规律：面积相同的多个长方形，以最长的边做底面周长卷起来的圆柱体积最大，以最短的边卷起来的圆柱体积最小;通过字母公式的推导还能进一步理解规律背后的原因。交流中学生的思维也正在逐渐进阶，从具体数据表象走向抽象推理，由表及里，从“是什么”走向“为什么”，深刻把握规律表象背后的知识本质。

阶段二：知识链接，脑洞大开。

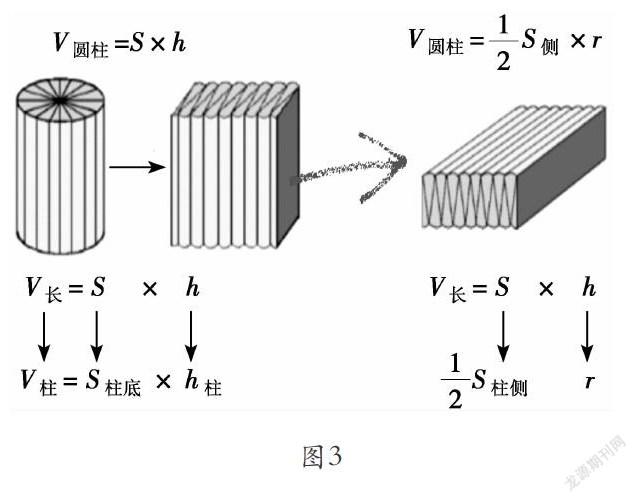
其实这和圆柱的另一个体积公式V= S×r有关呢！你会推导吗？你能利用这个公式，解释刚才从长方形卷成圆柱中发现的规律吗？

阶段二，再往外想一想，借助微课，了解圆柱的另一个体积公式：V=S×r，为学生理解规律提供了新的思考路径：当这些圆柱的侧面积相同时，体积和半径成正比例关系，半径越大，对应的圆柱体积也越大。由此打破学生已有的对圆柱体积公式的思维定势，刷新学生对圆柱体积公式的再理解，进一步丰富学生对圆柱体积的认知框架。

（作者单位：浙江省杭州市朝晖实验小学 本专辑责任编辑：王彬）