从现象到本质的数学模型的建构与应用

姚晶晶

【教学目标】1. 感受“餐饮店K与M开在一起”等多种类似生活现象的存在。

2. 经历思考、探索、阐释等学习过程，理解“餐饮店K与M开在一起”背后的数学原理。

3. 形成生活中处处有数学、生活与数学密切相关的数学意识，培养数学观察、数学思考、数学建模等核心素养。

【适合年级】六年级

【教学过程】

一、捕捉现象，提出猜想

出示一组照片：餐饮店K和M紧靠着开在一起。

引导：从这些现象当中，你有问题要问吗？

疑问：明明是竞争对手，K和M为什么要开在一起？

揭示课题：刚刚同学们依据自己的生活经验，从发现现象到提出问题，进而给出各种有依据的猜想，这是人们认识世界的一种重要方式。现象的背后究竟是什么？接下来，就让我们从数学的角度进行探究，一起去揭开K和M开在一起的奥秘。

二、应用模型，简化问题

1. 将复杂的空间问题简化为“直线模型”。

说明：如果在真实的生活场景下研究这个问题确实非常复杂，不妨用数学的方式把问题简化一下。

建构模型：假设有一条繁华的商业街道，它的长度大约是1千米。K和M这两家餐饮店同时看中了这块风水宝地，都想在这条街上开一家自己的店。假定这条街上的顾客都是均匀分布的，且每1米范围内就有一位顾客，那么这条街上一共就有1000位顾客。进一步假定：这些顾客对口味没有偏好，既可以吃K，也可以吃M。此外，他们的购买力也大致相等。

提问：根据上述条件，顾客到底是去吃K还是去吃M，你认为最主要的因素会是什么？

预设：距离——离谁近就买谁。

2. 推演模拟，做出判断。

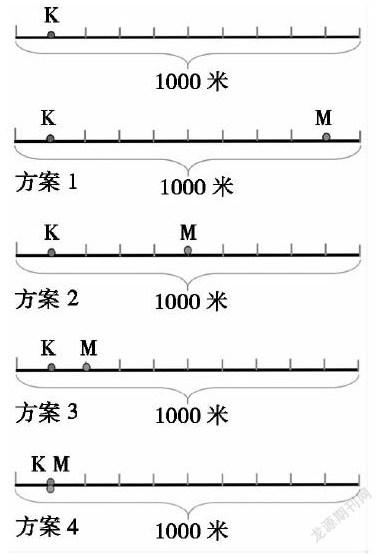
（1）任务一：K率先出手了，经理决定将店铺开在距离这条街最左边100米处。在这样的情况下，如果你是M经理，你会把店开在哪里？（约定：店铺要开在每个100米处的等分点上）

小组讨论，确定方案。

方案1：把M开在距离最右边100米处。理由：一个在左，一个在右，互不干扰。

方案2：把M开在这条街的中点处。理由：在中点就占据了核心位置。

方案3：把M开在K右侧100米处。理由：离K最近，能得到最多的顾客量。

方案4：和K紧紧地靠在一起，开在同一个点上。理由：两家店得到的顾客同样多，并且顾客的选择性会更大。既可以吃K，也可以选择吃M。

重点理解“开在一起”的含义：指两家店紧紧地挨在一起。左边的顾客两家平分，右边的顾客也两家平分。

几种方法各有利弊，学生可能对此争执不下。

点拨：要想做出准确的判断，仅仅依赖感觉是不可靠的。很多情况下，我们需要借助“数据”。

（2）优化方法，用数据说话。

方案1： M1=100+（800÷2）=500（人）。

右边的100人全部归M，两家中间的800人平分，所以每家400人，合起来M一共可以得到500人。

方案2： M2=500+（400÷2）=700（人）。

中点右边的500人全部归M，两家中间的400人平分，每家可以得到200人，M一共会有700人。

方案3： M3=800+（100÷2）=850（人）。

右边的800人全部归M，两家中间的100人平分，每家50人，M能得到850人。

方案4： M4=（900÷2）+（100÷2）=500（人）

由于它们紧紧靠在一起，左边的100人和右边的900人都是两家平分，因此每家各得500人。

有了数据的支持，预设会达成共识：选择方案③，即开在离K最近的右侧100米处。

三、提炼策略，渗透思想

1. 体会博弈过程。

提问：如果你是K老板，面对M所做出的决策，你又会做出怎样的反应呢？你还会固守原地吗？

预设：学生会将K移到M右边100米处（再次用数据证明想法，图略）

K=700+50=750（人），M=200+50=250（人）。

说明：无论是K还是M，它们都在追求利益最大化。它们之间互相比拼、彼此对抗以获得利益最大化的过程，数学上把它称作博弈。

提问：这场博弈会在这里终止吗？会不会永远继续下去？

任务二：假设博弈还将继续下去，这场为了争夺客源的博弈大战总有停下来的那一刻，猜一猜：这两家店最终会停在什么位置上？

学生讨论，各自给出设想方案。

2. 优化博弈策略。

方案1：K开在距离中点左边100米处，M开在距离中点右边100米处。

方案2：M开在中点，K开在靠中点左边100米处。

方案3：两家一起开在了中点处。

比较三种方案，你更認同哪一种，说一说理由（图略）。

理由1：第一种方案，看似稳定，但只要其中一方往中点移动，就会占据更多客源，所以还是会继续博弈下去。

理由2：第二种方案，K明摆着吃亏，所以也不会让博弈停止。

理由3：第三种方案，两家通过不断地互相比拼、博弈，最终只能共同占据中点位置。这样的好处是，首先，两家店都能平分到500人的客源。其次，无论是谁，都不敢再轻易移动了，谁移动了谁就会吃亏。所以，一起开在中点，是最稳定、最保险的，是两家利益均衡的最好选择。

追问：这对欢喜冤家是开开心心在一起还是无可奈何在一起？

归纳：博弈的最终结果并不是谁赢谁输，而是相互妥协，找到一个平衡点，让双方得到的利益能够均衡且稳定，这是博弈现象当中很有意思的一种策略。今天，同学们通过模拟推演，既揭开了K和M会开在一起的秘密，同时对这种现象背后所隐藏的“均衡博弈”思想也有了一定程度的体会和思考。

四、拓展迁移，内化提升

迁移：在你的生活当中，除了K和M，你有见到过其他类似的现象吗？

小结：这节课，我们并没有学习任何知识，但是，我们却多了一种用数学看待世界的眼光和思考方式。数学，仅仅是用作解题的吗？它更大的用处在于能够帮助我们透过现象，看到事物的本质。而这，才是我们学习数学更为重要的价值所在。

（作者单位：江苏省南京市锁金新村第一小学？摇？摇？摇责任编辑：王彬）