基于改进樽海鞘群算法的无线传感器网络节点定位*
田洪舟,陈思溢,黄辉先
(1.湘潭大学 自动化与电子信息学院,湖南 湘潭 411105;2.广东科技学院 计算机学院,广东 东莞 523000)
0 引 言
节点定位技术是无线传感器网络(wireless sensor networks,WSNs)中一种重要的基础技术,如何提升节点定位的精度成是一个受人关注的问题。节点定位的常用方法主要分为基于测距的定位算法和基于非测距的定位算法两种,其中,距离矢量—跳数(distance vector hop,DV-Hop)算法是基于非测距的定位算法中应用最广的一种,具有消耗资源少,需要信标节点数少,实现简单等优点。
基本的DV-Hop算法在定位时受节点分布的影响较大,其结果并不十分准确。研究人员提出了多种改进的方法,其中大部分文献采用了在DV-Hop算法的前两个阶段精确跳数和平均跳距的方法达到减少定位误差的目的[1~4]。也有学者提出了在定位阶段用智能优化算法代替最小二乘法来减小计算误差。如文献[5]提出用遗传机制改进的粒子群算法优化DV-Hop算法,定位的精度明显高于原算法;文献[6]融合了免疫算法与粒子群算法,改进了浓度机制,动态调整了疫苗范围,提高了定位精度;文献[7]引入数学优化模型限定人工蜂群的寻优范围,降低了定位误差且减少了计算量;文献[8]利用了布谷鸟和差分进化双种群搜索,动态调整了布谷鸟算法中发现入侵者的概率,并随机缩放差分进化的变异算子,得到了较好的定位精度。但智能优化算法具有收敛速度较慢,容易陷入局部最优的缺点,如何改善这些缺点使其更好地优化DV-Hop算法是一个值得关注的问题。
本文提出了用精英引导变异和败者淘汰策略改进的樽海鞘群算法优化DV-Hop算法中的定位误差。由于本文所提算法只在DV-Hop算法的位置估计阶段进行优化,所以对传感器的硬件要求没有影响。
1 DV-Hop算法与改进目标
DV-Hop算法可分为三个主要阶段:1)信标节点通过广播自身信息,使网络中所有节点记录下各信标节点的坐标及相应的最小跳数。2)信标节点接收到其他信标节点的消息后,按式(1)计算自身的平均跳距,每个未知节点用平均跳距和跳数相乘,就可估算出未知节点与各信标节点之间的距离。3)当未知节点计算出与各信标节点的距离之后,利用最小二乘法便可求得未知节点的估计坐标。式(1)计算如下
(1)
式中 (xi,yi),(xj,yj)为锚节点i,j的坐标,hi为它们之间的跳数。
DV-Hop算法的定位误差与网络中节点的分布均匀程度相关,且待定位节点采用最近的信标节点的平均跳距作为自身的全局平均跳距也会引起较大定位误差。因此,由第一第二阶段得到的未知节(x,y)点与锚节点A1(x1,y1),A2(x2,y2),…,An(xn,yn)的距离d1,d2,…,dn是存在误差的,如下式所示
(2)
式中ε1,ε2,…,εn为第一阶段和第二阶段产生的误差。则总误差如下
(3)
式中n为锚节点数量。因此,DV-Hop第三阶段求解未知节点可以看作是求总误差最小的非线性优化问题,可以应用智能优化算法求解。
2 基于改进樽海鞘群算法的DV-Hop算法
2.1 樽海鞘群算法
2017年,樽海鞘群算法(salp swarm algorithm)作为一种结构简单,输入参数少,易于实现的全新群体智能算法,由Mirjalili S等人提出[9],受到了许多学者的关注并将其应用于实际问题[10~13]。樽海鞘群初始位置随机在搜索空间中产生,并定义一个适应度最高的个体为食物源,称为F,作为群体的目标。然后将种群划分为领导者和追随者两部分,采用以下公式更新领导者的位置
(4)
式中ubj和lbj为搜索空间的上下界。c2和c3为[0,1]间的随机数,c2决定了向第j维空间的下一个位置移动的长度,c3则决定朝着正向或是负向移动,是方向控制参数。c1为平衡进化中搜索和开发能力的最主要参数,其定义如下
(5)
式中t为当前迭代次数,Tmax为最大迭代次数。
而追随者的位置采用以下公式(牛顿运动定律)更新
(6)

(7)
由以上可知,樽海鞘链的行为机制可由式(4)和式(7)模拟。
2.2 Cat混沌映射种群初始化
大部分群体智能算法采用的是随机方法生成初始种群,但这就有可能使部分解远离最优位置,而混沌序列具有的不规律性,随机性及遍历性的特点使其可以产生分布均匀的种群。由文献[14]可知,Cat映射的遍历性好,且不易陷入小循环和不稳定周期点,能生成更好的均匀序列,因此本文采用Cat映射生成种群的初始位置。Cat映射是可逆的二维混沌映射,其数学表达式如下
(8)

(9)
式中 [lbi,ubi]为搜索空间的范围。
2.3 精英引导变异
由樽海鞘群算法的追随者更新公式可知后一个体的位置更新主要依靠前一个个体,具有盲目性和不确定性,容易导致早熟收敛,陷入局部最优。所以,为了提高追随者对环境的探索能力,应该在更新中加入环境和适应度最好的个体即食物源的影响,本文提出了一种精英引导变异的方法,对式(7)进行改进,新的追随者更新公式如下
(10)
式中i≥2,k=1/t2为自适应系数,t为当前迭代次数;(1+φr)为环境干扰算子,φ为干扰程度,一般取2;r为[-1,1]的随机数。由式(10)可知,随着迭代的进行,变异空间逐渐递减,开始较大的变异空间可以搜索更多位置,而后期较小的变异空间有助于提高寻优精度。
2.4 败者淘汰策略
在种群的进化中,进化程度较慢的个体容易被淘汰。但它们可能在不同的地方发展和进化,减少面对的直接竞争,最终生存下来。在自然界和人类社会中,这种现象十分普遍,这是一种避免局部最优和保持多样性的方法。也就是说,淘汰掉失败者后,重新生成一个进化程度较高的个体加入搜索,加大了寻找最优解的机率。
首先定义第g代种群中第i个个体的进化程度δ为
(11)
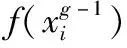
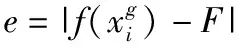
(12)
将该个体加入种群中使种群向最优位置进化。
2.5 改进的DV-Hop算法流程
1)在指定范围内随机部署若干个锚节点和待定位节点,利用DV-Hop算法第一、第二阶段估算锚节点和未知节点的距离。2)用Cat混沌映射初始化樽海鞘种群,按式(3)计算适应度值。3)将个体按适应度值排序,适应度最好的个体位置选定为食物源位置。4)设定前50%适应度高的樽海鞘个体为领导者,根据式(4)更新,后50%为追随者,根据式(10)更新。5)败者淘汰策略比较个体进化程度,并利用式(12)更新进化程度较低的樽海鞘个体。6)种群更新后,重新计算每个个体的适应度值,并更新食物源位置。7)重复步骤(4)~步骤(6),若达到规定的最大迭代次数,算法停止运行,并将食物源位置即未知节点估计位置输出。
3 实验与结果分析
采用在仿真软件MATLAB(R2016a)上进行仿真实验。选取实验区域的大小为100 m×100 m,区域内节点总数为100个,其中锚节点20个,节点的通信半径为30m。选取PSO优化的DV-Hop算法,文献[15]提出的自适应调整策略灰狼算法(记为IGWO)优化的DV-Hop算法进行对比,所有算法的种群数量设置为20,迭代次数设为100次,算法的适应度函数为式(3)。为减少偶然性,优化结果取30次实验的平均值。为了体现定位误差的变化,采用归一化的相对误差来评价算法的定位性能。归一化定位误差的计算公式如下
(13)

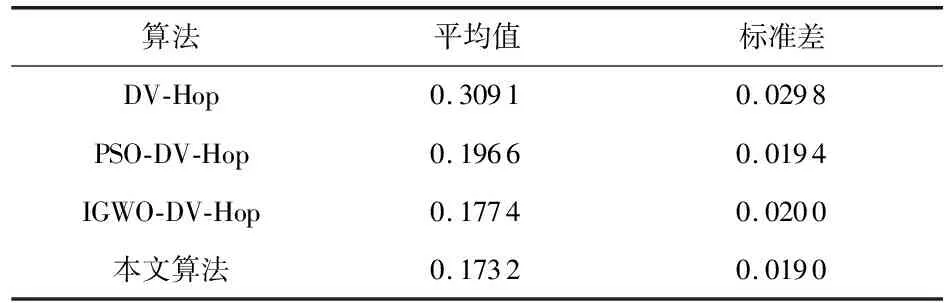
表1 定位算法的归一化平均误差与标准差
从表1中可以看出,本文算法的归一化平均误差和标准差都小于其他算法,说明除了定位精度较高之外,定位的波动性也较小,具有更好的定位稳定性。
锚节点比例、节点通信半径、节点总数对定位性能影响仿真实验结果如图1所示。
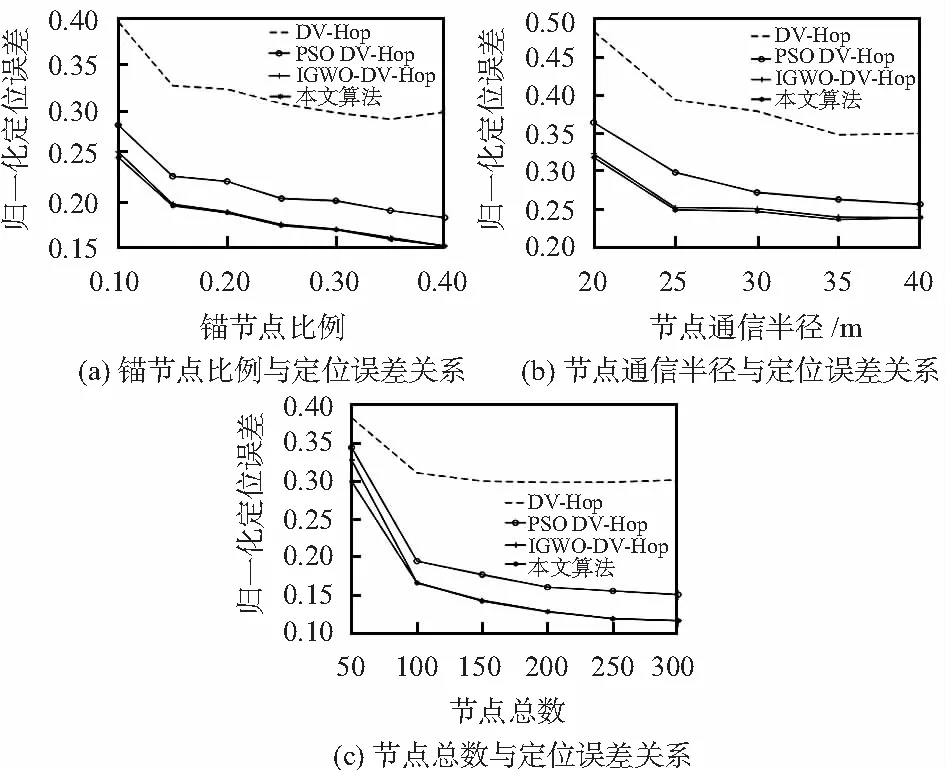
图1 仿真实验结果
1)锚节点比例对定位性能的影响:设置节点总数为100个,节点通信半径为30 m不变,通过改变锚节点比例测试对定位性能的影响,仿真结果如图1(a)所示。可以看出随锚节点比例上升所有算法的定位误差都在减小,其中本文算法的准确度最高,本文算法的定位精度比三种对比算法分别高了约14.8 %,3.9 %,0.6 %。
2)节点通信半径对定位性能的影响:设置节点总数为100个,其中锚节点10个不变,通过改变节点通信半径测试对定位性能的影响,仿真结果如图1(b)所示。由图可知随通信半径变大定位误差会减少,但在大于35 m时,定位误差出现了微小的上升。这是因为通信半径增大到一定限度后,继续增加会加大锚节点每跳距离的误差,从而使定位误差小幅上升。从图1(b)中得出,本文算法比其他三种定位算法的误差分别减少了约16.5 %,4 %,0.7 %。
3)节点总数对定位性能的影响:设置锚节点比例为30 %,节点通信半径为30 m,通过改变节点总数测试对定位性能的影响。仿真结果如图1(c)所示。节点总数的增加使网络连通度变大,节点之间的距离变短,DV-Hop算法第一、第二阶段估计的跳数和平均跳距更准确,定位的性能会越好,所以图1(c)的三种优化后的DV-Hop算法误差都在减少。其中,节点总数为50时,平均跳距的误差较大。本文算法的优化效果比较显著,误差分别减少了8.3 %,4.4 %,2.8 %。节点总数为100以上时,平均跳距误差变小,定位结果趋于收敛,本文算法的定位误差比其他三种算法分别减少约14.4 %,2.8 %,0.1 %。
4 结束语
为了提高DV-Hop定位算法的准确率,本文提出了改进的樽海鞘群算法,使用Cat混沌映射初始化种群,加入了精英引导变异和败者淘汰策略,使算法加快了收敛速度,提高了寻优能力。将改进的樽海鞘群算法应用于DV-Hop算法第三阶段,仿真结果表明:在不额外增加硬件和能量开销的情况下,优化后的DV-Hop算法准确率明显优于传统的DV-Hop算法,和其他智能优化算法的对比中定位误差也较小,具有更好的定位能力。

