基于双层路径优化算法的多机器人最优编队方法*
周佳加, 张 强, 王宏健, 张洪泉, 王莹莹
(哈尔滨工程大学 自动化学院,黑龙江 哈尔滨 150001)
0 引 言
随着机器人技术的发展,多机器人编队的需求与日俱增,其中最基本的行为是编队,其主要解决机器人之间协调问题。编队涉及到每个机器人的路径规划,即在一定约束下,编队中的每个成员从规划空间中寻找出从初始姿态到期望位置的路径。当编队任务有时间约束时,快速形成指向任务点的编队,有效节省了完成任务的时间,且增强了编队任务的机动性。1957年Dubins提出[1]在某个曲率的约束的条件下,可在同一平面内寻找出任意两个矢量点的最短路径。Yeol J W 等人[2]采用Dubins路径的方法求取了二维水平面两点间的最短路径,并通过微积分将这种方法给予了证明。Teng L等人[3]提出了一种多无人机攻击多个地面目标的任务规划方法。戴健等人[4]采用“Z”型路径覆盖方法以及Dubins转弯路径,对各个无人机开展覆盖其子区域的搜索路径规划。Peng C等人[5]提出了一种具有姿态约束的移动机器人路径规划方法规划出一条无障碍路径。胡永文等人[6]针对每个人和任务的最短时限指派问题提出求解最短时限指派问题的快速决策方法。Burgard W 等人[7]采用匈牙利算法求解出了最优分配方法。宗群等人[8]通过粒子群和遗传优化算法双层优化解决大规模集群编队中队形选择和站位分配问题。
本文对多机器人编队路径规划问题进行分析,根据编队时间、编队位置分配等约束建立了相应的问题模型,设计了将粒子群优化(particle swarm optimization,PSO)与连续Hopfield神经网络(continuous Hopfield neural network,CHNN)的双层路径优化的方法求解出最优编队方法。最后通过仿真实验验证了本文提出方法的有效性。
1 多机器人编队问题描述与建模
假设机器人初始队形中编队成员在地面坐标系下第i(i=1,2,…,n)个机器人的坐标表示为(xi,yi),ψd表示期望编队方向,而机器人路径规划空间由机器人最大航程决定。
定义双层规划模型为
(1)
式中P和L为双层优化结果,f和g为优化模型的性能指标,G为优化模型的约束指标,a1,a2,…为优化有关参数。
1.1 约束指标
在多机器人编队中,根据机器人的欠驱动性和任务,还需考虑以下四个约束[9,10]:
1)编队到达期望队形时的位置与航向约束
(2)
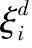
2)编队过程的能耗约束
(3)
式中W为编队过程中机器人总能耗,li为机器人i的路径长度,k1为常数。
3)机器人最小转弯半径的约束
最小转弯半径用如下公式表示
ρmin=f(max,U)
(4)
4)编队时间约束
假设在编队过程中机器人速度v没有太大波动,则定义参数k2=1/v,编队时间定义为
T=k2lmax
(5)
式中lmax为路径最长的机器人路径长度。
1.2 优化目标
在三角编队中,选取编队完成期望点Pk,再计算第i个机器人到达期望编队中第j个位置的距离lij,进而计算出编队过程的总耗费(总路径)定义优化目标函数
(6)
式中Wmin为编队集结点k下的最少能耗,lall为所有机器人到编队中期望位置的路径总长度,Tmin为最短编队时间,lij为机器人i到编队中期望位置j的路径长度。
2 双层路径优化算法
2.1 基于PSO的编队集结点优化
假设由m个粒子组成的种群X=(x1,x2,…,xm)在搜索空间D中,则第i个粒子在k+1次迭代时速度和位置更新方法为
(7)
式中w为惯性权重;d=1,2,…,D;i=1,2,…,m;k为迭代次数;Vid为粒子的速度;c1和c2为非负的常数,称为加速度因子;r1和r2为分布于[0,1]之间的随机数。将位置和速度分别限制在[-Xmax,Xmax],[-Vmax,Vmax]之间。
为了更好平衡算法全局搜索和局部搜索的能力,本文设置权重为递减形式[11],初始权重为ws,终止权重为we,则权重的更新方式为
(8)
2.2 基于CHNN的路径优化
在编队虚拟集结点Pk约束下,设n个机器人和编队期望位置,第i个机器人为Ri,机器人编队中第j个位置为R′j,j=1,2,…,n,在编队虚拟集结点Pk下Ri到R′j的路径距离为lkij。则系数矩阵为
(9)
引入变量xkij
(10)
指派每个机器人到相应位置的最优分配问题的模型为
(11)
(12)
其中,在k(k=1,2,…,m)个编队虚拟集结点下每个机器人在总路径最少的约束下到达期望位置的最优位置分配方法。式(12)表示矩阵Xk=(xkij)n×n的行列约束和取值范围。
将每个机器人从初始位置i到编队虚拟集结点Pk队形中的位置j作为一个变量,每个神经元处理一个变量xkij,故整个网络中神经元个数xkij应该个数相等。
则神经网络的能量函数Ek[12]
(13)
式中λ1,λ2为拉格朗日加权系数。能量函数前两项为行列约束,使得xkij每行每列有且仅有一个1,即每个机器人对应一个期望队形中的位置;第三项表示总能量耗费约束,即整体路径最短。
(14)
式中xkij为神经元(i,j)的输出,ukij为神经元(i,j)的输入,xkij=f(ukij),f函数为神经元(i,j)的输出函数,可以有不同的规律,这里选取Sigmoid函数
(15)
网络输入初始化
ukij(t)=u0ln(n-1)+δkij
(16)
其中,设置u0=0.1;n为机器人数量,δkij为区间[0,1]的随机数;导入优化参数lkij。
网络按照下面方式运行
(17)
式中 Δt为单步时间;ukij(t)为t时刻的神经元输入。
2.3 双层优化算法实现
1)初始化粒子群位置和速度,包括权重wk,加速度因子c1和c2等。2)第一层优化计算,以当前粒子位置为编队集合点,为每个机器人选择合适的Dubins路径,并计算系数矩阵。3)第二层优化计算,采用CHNN算法求解在此系数矩阵下,每组机器人的最优位置分配方法和适应度,第二层优化结束。4)根据适应度更新局部和全局最优集结点,初始优化完成。5)根据迭代次数更新位置、速度和权重w(k)。6)以当前粒子位置为编队集合点,为每个机器人选择合适的Dubins路径,并计算系数矩阵。7)第二层优化计算,采用CHNN算法求解每组机器人的最优位置和适应度,第二层优化结束。8)根据PSO迭代次数判断迭代是否完成,完成则算法结束,否则返回步骤(4)。
3 仿真实验与分析
本文采用MATLAB 2016a进行仿真实验,规划空间为{(xi,yi)|-100≤xi≤500,-100≤yi≤400},3个欠驱动机器人组成的编队,转弯半径ρ=60 m,初始坐标随机分布在[-100,100],初始方向角为130°,60°,270°,期望编队能在B=(400,230)前完成编队。
采用式(7)PSO算法公式更新位置和速度,取100个粒子,进化次数为200,式(8)中取惯性权值参数ws=0.95,we=0.35,学习因子c1=c2=1.5。式(13)、式(14)中,λ1=150,λ2=80,采样时间取0.001,迭代次数取1 000。
图1(a)是静态权重PSO算法求解最优编队集结点的适应度曲线,在迭代180次时接近最优值276,图1(b)改进PSO算法在迭代20次时接近最优值276,求出最优编队集结点(276,156)。固定惯性权值全局搜索和局部搜索无法兼顾,时变的惯性权重则前期有较强的全局搜索能力,后期更有利于精确的局部搜索。

图1 静态/动态权重PSO算法适应度曲线
图2是最优编队集结点下采用CHNN分配方法的能量函数,从图中可知CHNN的能量随着迭代次数逐渐降低。在能量变化率趋于0时,整个网络逐渐接近平衡态,则求得的各航行器最优分配路径。
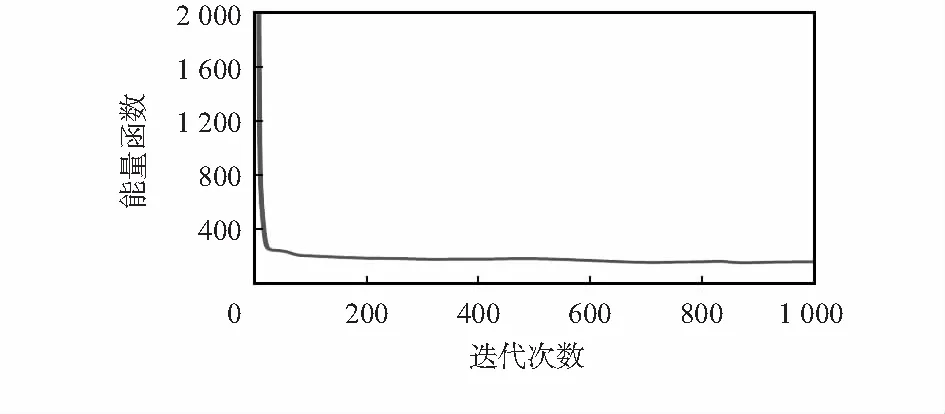
图2 CHNN能量函数
图3为机器人完整的编队路径图,编队初始位置在图左下角,指向设定编队集结B点前行,并在A点完成编队。
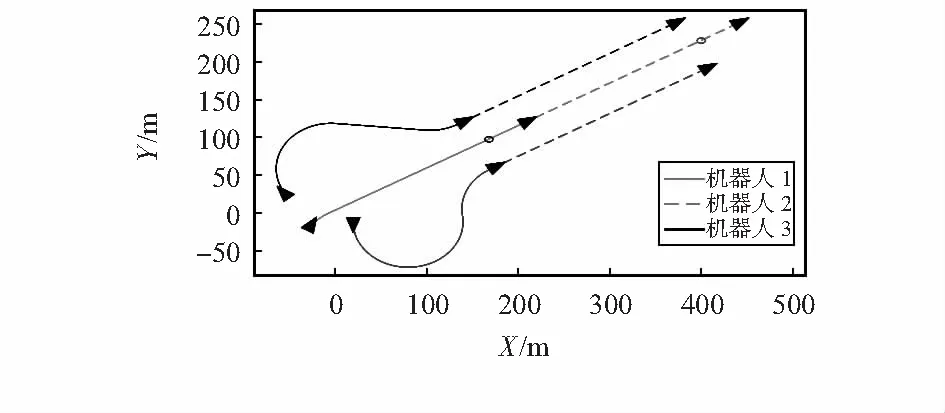
图3 改进粒子群算法路径仿真
4 结 论
针对多机器人编队集结点的优化问题,本文提出了一种多机器人编队双层规划模型。第一层解决了最优队形编队集结点规划问题,在时间约束上采用改进PSO算法求取在编队时间最短的最优编队集合点,并利用动态递减的权重平衡了PSO算法全局与局部的搜索能力。第二层解决了编队中成员位置分配问题,基于Dubins路径采用CHNN算法将编队中的机器人成员以最小能耗的条件下分配到最优位置。最后,通过欠驱动机器人的编队仿真实验表明所提算法正确、有效。

