基于LMS与MAF的MEMS陀螺降噪算法*

胡 佳, 蔡成林,2

(1.桂林电子科技大学 广西精密导航技术与应用重点实验室,广西 桂林 541000；2.湘潭大学 智能导航与遥感研究中心,湖南 湘潭 411100)

0 引 言

随着微机电系统(MEMS)技术的发展,MEMS陀螺以其独特的优势逐渐取代其他类型的陀螺,在民用惯性导航系统中广泛应用[1]。陀螺是惯性导航设备中最重要的器件,用于测量载体的角速率,它的精度直接决定了惯性导航系统的精度[2～6]。MEMS陀螺易受温度、电磁环境等因素的影响[7],导致其输出中存在噪声,一方面在其本身固有的物理结构,会受到电磁干扰、机械噪声的影响,会使其灵敏度、精度大幅下降[8];另一方面,由于陀螺仪对周围环境如外界振动、温度变化以及其他随机扰动等非常敏感,也存在较大的随机漂移误差。因此,分析MEMS陀螺的噪声误差特性,降低噪声误差成为实际应用中亟待解决的关键问题。

为了降低陀螺噪声误差对惯性导航系统的影响,本文对MEMS陀螺噪声进行了研究,首先研究最小均方(least mean square,LMS)法并且进行改进,然后量化分析移动平均滤波(moving average filtering,MAF)降噪效果,最后将二者进行组合,分别与dB5小波降噪以及传统LMS进行对比。最后建立实验方案验证其普适性,通过Allan方差(AV)法对采集的数据滤波前后的各项噪声进行量化分析。

1 LMS算法

LMS算法是自适应研究中简洁有效且可实际应用性最强的算法[9,10],是由 Widrow 和 Hoff两位学者最先提出并使用的,具有简单、易实现的优点。输入信息先验统计性不得知时解得滤波器参数。为了不依赖于输入先验信息,LMS算法的中心思想把最速下降法均方差转变成瞬时误差平方值,并以其梯度成为均方误差函数梯度的估计值。设计LMS自适应滤波器的最普遍的结构就是横向滤波器结构,输出信号y(n)为

(1)

式中N为滤波器的阶数,wT(n)为权系数的转置矩阵。滤波器权系数

w=R-1*P

(2)

设w(n+1)表示n+1时刻的滤波器系数权矢量,根据最速下降法,滤波器权系数递归迭代公式表示为

w(n+1)=w(n)+μ(n)x(n)*e(n)

(3)

式中μ(n)为自适应步长,用来控制滤波器算法收敛性和稳定性。对于LMS算法为了保证收敛,μ(n)的取值范围为0<μ(n)<2/λmax(λmax为输入信号x(n)的自相关矩阵的最大特征值)。LMS算法流程如图1所示。

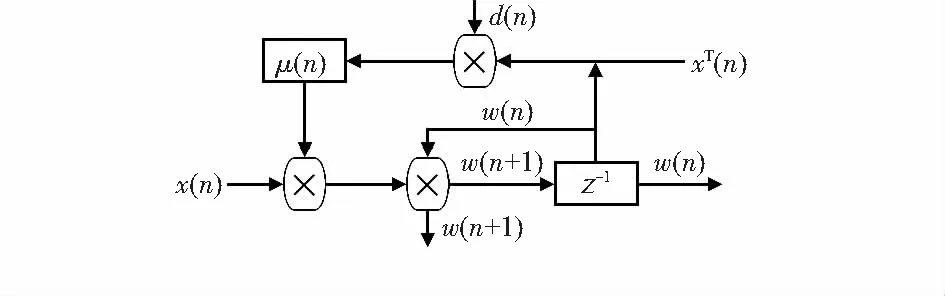
图1 LMS算法流程图

2 MAF算法

移动平均滤波器是一种有限冲击响应型低通滤波器,在处理特定次谐波时有较强的衰减能力,并且算法结构简单,在稳态时滤波效果极好。MAF算法由于实现原理非常简单,时间复杂度较小,滤波性能优异,因此广泛应用于信号的随机噪声处理中。移动滤波技术可以从预期数据中过滤掉不需要的噪声成分,有效地用于对惯性传感器信号进行降噪。通用滑动滤波的表达式为

(4)

式中x为(i+j)时刻的输入信号,y为i时刻的输出信号,M为滤波器阶数,等于滑动窗口宽度。M的选择对于信号的平滑程度至关重要。如果M非常大,则平滑可能会移除与信号相关的显著低频分量。如果M太小,则只能去除最高频率的噪声,并且可能仍会保留一些噪声。

3 LMS-MAF降噪算法

由于LMS 算法与MAF算法在处理噪声中均有较好的效果,但有各自存在一些不足,因此本文提出了一种基于LMS-MAF的降噪算法,对LMS 算法与MAF算法取长补短。首先使用LMS 算法将陀螺数据进行平滑处理,通过调节滤波器参数加快收敛速度,但会使性能降低,然后使用MAF降噪算法针对特定次谐波进行降噪。LMS 算法预处理:利用LMS 算法预处理MEMS陀螺信号。由于LMS算法的收敛速度和收敛性都与μ(n)息息相关,而本文提出的算法在经过LMS预处理后还会使用MAF进行特定滤波,因此，LMS在预处理中通过牺牲掉部分精度来获取更快的收敛速度。这里针对μ(n)的计算进行了改进

μ(n)=β(1/(1+exp(-α|e(n)e(n-1)|2))-0.6)

(5)

前面已经针对步长μ(n)做出了限制,必须满足0<μ(n)<2/λmax,上式最大值为β,所以，α和β作为调节系数不仅要遵循步长调节公式,而且也需要满足0<β<2/λmax。改进后的算法降低了LMS算法对输入噪声的敏感性,同时也提高了收敛速度,具有稳态误差小的优点。

AV是一种常用的时域方法,被广泛应用于MEMS陀螺所包含的随机误差与噪声性质的识别和量化中,AV法最大的优点是可以简便细化分离、辨识MEMS陀螺的各项误差,同时确定各个误差项对总误差的贡献。一般认为噪声项包含角随机游走、量化噪声、零偏不稳定性、速度斜坡、速度随机游走等。

4 MEMS陀螺信号降噪实验与分析

为验证本文提出的LMS-MAF算法对MEMS陀螺仪降噪的效果,将ADI某型陀螺仪(图2所示)静置于工作台一段时间,待器件稳定后以100 Hz的频率进行采样,采样时间为1 h。然后分别采用LMS算法、dB5小波降噪以及所提方法进行降噪处理。

图2 实验传感器平台

通过图3可知,三种算法均有一定的降噪效果,所提算法相比传统的算法效果更加显著,通过图4的AV曲线以及表1中噪声系数分析可以看出所提算法在角随机游走、量化噪声、零偏不稳定性、速度斜坡、速度随机游走[11]系数均有90 %以上程度的降低。

图3 原始信号及不同降噪后的时域图

表1 噪声系数统计

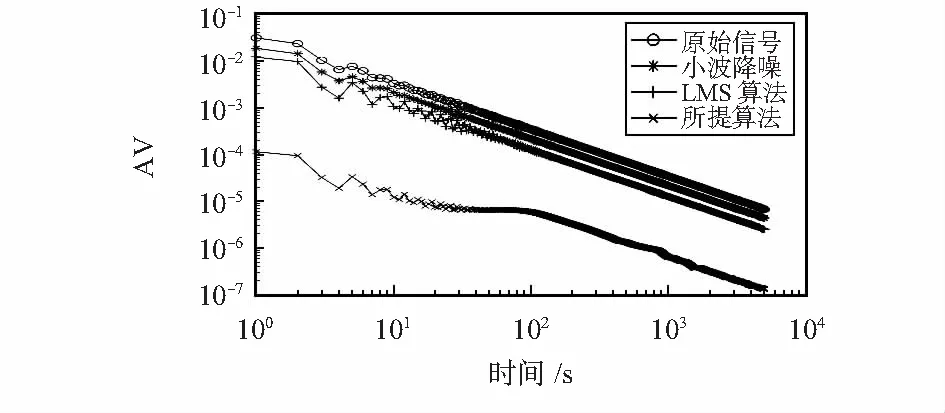
图4 AV曲线

由前面可知,MEMS陀螺的输出在经过所提算法处理后,噪声幅值水平得到了明显的抑制。下面分别选取相同滑动窗口长度M,不同初始收敛因子MU；相同初始收敛因子MU,不同滑动窗口长度M进行测试。由图5以及表2可以看出:随着MU减小、M增大,噪声抑制效果也变好。

图5 不同初始状态的时域图

表2 不同初始状态均值和标准差

5 结 论

为了降低MEMS陀螺信号中的噪声分量,本文提出了一种改进LMS-MAF算法的陀螺信号降噪方法。利用MEMS陀螺的输出信号验证算法的性能。结果表明：在实测环境下采用本文提出的算法对MEMS陀螺信号进行滤波,与dB5小波降噪以及LMS算法进行了比较,证明其滤波性能优于二者。使用AV分析法对滤波前后陀螺仪信号进行定量分析,验证了该方法对MEMS陀螺信号降噪的有效性。