两自由度直驱感应电机转子结构设计与优化研究*

李祎博, 封海潮, 汪旭东, 许孝卓, 鲁建锋

(河南理工大学 电气工程与自动化学院,河南 焦作 454000)

0 引 言

近年来,随着智能制造的不断升级发展,对驱动装置提出了更高的要求,传统的单自由度电机已不能满足工业生产和生活的需要[1]。两自由度直驱感应电机(two-degree-of-freedom direct drive induction motor,2DoFDDIM)是一种新型的可以做直线、旋转以及由两种运动复合而成的螺旋运动的电机[2]。其定子部分整体为圆筒形,由旋转和直线两部分弧形定子沿周向扣合而成,转子部分采用实心转子结构[3]。由于实心转子结构的特殊性,在电机运行的过程中涡流和磁通集中分布在转子表面,增大了转子表面的电阻和附加损耗,导致实心转子出力较小,效率和功率因数偏低[4,5]。

在对电机结构进行优化设计时,通常选取电机的某一结构参数作为优化变量,对所选参数选取不同水平值进行分析,得到最优的参数水平值。采取单一变量的优化方法忽略了不同参数间的相互影响,难以得到最优的参数组合,实现电机性能的最优设计[6,7]。

为了实现对电机性能的多目标优化,国内外学者做了大量的研究[8～11]。其中，遗传算法、蚁群算法、粒子群算法等都是全局优化设计算法,具体目标函数的建立较为复杂,求解耗时较长,很难实现电机最优结构参数组合的快速搜寻[12]；田口法是由日本田口玄一博士提出的结合正交实验和信噪比技术建立的一种优化设计算法,因其具有以最少的实验次数来实现对最优参数组合搜寻的能力,被广泛应用于电机多目标优化设计领域[13]。

为了研究2DoFDDIM的目标性能和不同参数间的关系,本文引入了田口优化算法对电机的旋转部分特性进行优化。针对开槽铸铜转子的槽参数对电机性能的影响,选取了开槽宽度、开槽深度和开槽尺寸等对电机性能影响较大的参数作为优化变量,搜寻最优的参数组合,实现电机综合性能的提升。

1 2DoFDDIM结构与主要参数

2DoFDDIM的定子沿中轴线剖开,旋转部分弧形定子为180°,与动子构成旋转感应电机；直线部分弧形定子为140°,与动子构成弧形直线感应电机；转子部分最基本的结构为实心转子结构,两种转子结构2DoFDDIM示意图及参数如图1和表1所示。

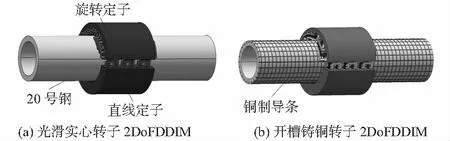
图1 两种转子结构2DoFDDIM示意

表1 电机主要参数(旋转部分)

2 不同转子结构2DoFDDIM特性分析

2.1 涡流及磁场分布

2DoFDDIM在正常工作状态下的转差率为0.2～0.4,图2为转差率s=0.3时两种不同转子结构电机的磁场及涡流分布图。由转子涡流及磁场分布的截面示意图可以看出,光滑实心转子的磁力线分布存在偏移。由于受集肤效应的影响,涡流主要分布在转子表面,并在转子表面产生一个横轴磁场。在横轴磁场和主磁场相互作用下,与主磁场同方向时起到矢量相加的作用,在转子表面高度饱和的情况下,继续增磁会使合成磁场进入相邻磁极的下方,因此,磁力线方向沿着转子的旋转方向被拉伸。

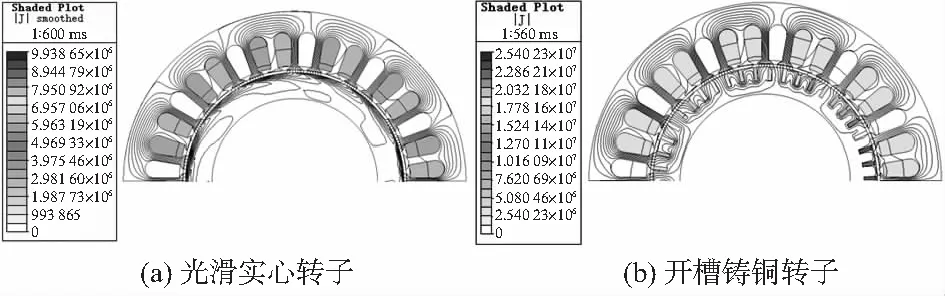
图2 s=0.3时两种不同转子结构电机的涡流及磁场分布截面

开槽铸铜转子的磁力线在同一个转子齿两侧磁力线的分布密度不同。大部分磁力线沿齿槽轮廓线闭合,磁场透入深度比光滑实心转子更深,有更高的输出转矩及效率。

部分磁力线越过槽部闭合,使开槽铸铜转子有较大的漏抗,铸铜导条改变了转子涡流的流通路径,降低了转子表面的附加损耗,同时铸铜材料的电阻率低使其阻抗较小,因此,在小转差率情况下,开槽铸铜转子电流较大,其感应电动势小于光滑实心转子,具有更小的励磁电流,使开槽铸铜转子电机有更大的输入电流和更高的功率因数。

2.2 特性计算与对比

建立2DoFDDIM的旋转部分的二维有限元模型。两种不同转子结构2DoFDDIM旋转部分的转矩、效率、功率因数特性随电机转差率变化的计算结果如图3所示。

图3 不同工况下的电磁转矩、效率及功率因数对比

由图3可知,2DoFDDIM采用光滑实心转子结构时旋转部分的转矩随着转差率的增大而逐渐增大,在转差率为1时达到电磁转矩的最大值,这是由于光滑实心转子结构电机的临界转差率较大,其最大转矩发生在电磁制动状态,同时也是实心转子结构电机工作特性较软,效率和功率因数较低的原因。

在2DoFDDIM采用开槽铸铜转子结构时旋转部分的转矩随着转差率的增大呈现先增大后减小的趋势,在转差率为0.5时达到转矩的最大值。转子采用开槽铸铜结构时降低了电机的临界转差率,使其折算至定子侧的转子阻抗变小,改善了电机的运行特性。

在正常工作状态下s=0.3时,对有限元软件求解的数据进行进一步分析计算,两种不同转子结构2DoFDDIM旋转部分的性能指标计算结果如表2所示。

表2 两种转子结构电机性能对比

其中,效率的计算公式为

(1)

式中P2为电机的输出功率,P1为电机的输入功率,PFe1，PFe2分别为定、转子铁损耗,PCu1，PCu2分别为定子绕组铜损耗和转子铜条涡流损耗,P0为转子铸钢材料的涡流损耗,忽略机械损耗和附加损耗的影响。

从有限元计算结果可以看出,在应用开槽铸铜转子时电机在各方面的性能都优于光滑实心转子。但转子表面开槽铸铜导条时由于铜材料的磁阻较大,相当于增大了电机的等效气隙,因此，转子开槽的尺寸会对电机的综合性能产生影响。同时又受限于转子尺寸的约束,转子的开槽数量也需进一步选取。

3 覆铜开槽转子结构参数优化

3.1 设计方法及目标

在田口法正交实验中,选取覆铜开槽转子的开槽深度d，开槽宽度w，开槽数量n为优化参数,每个参数选取五个影响因子水平,其影响因子水平见表3。选取旋转部分的转矩T(N·m),转矩波动TR(%),效率η,功率因数λ,转矩电流比Ti(N·m/A)为优化目标。

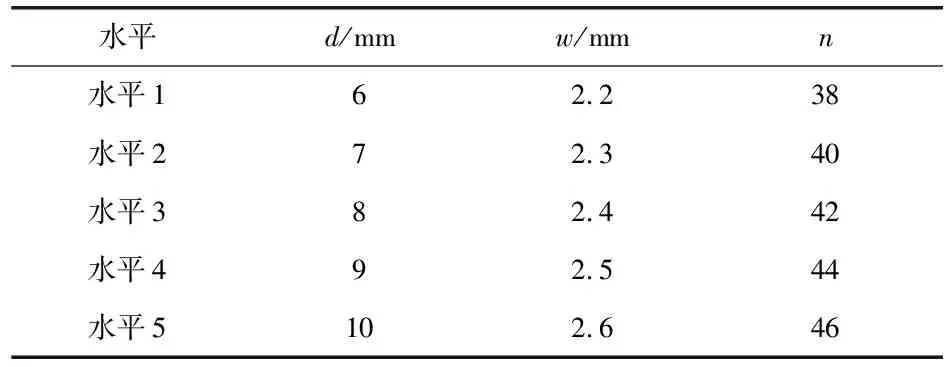
表3 参数的影响因子水平

3.2 正交实验求解及有限元结果

实验选取3个影响因子为变量,每个变量的因子水平数为5,该正交矩阵代码为L25(53)。按照传统单一变量优化的方法,需要进行53=125次计算,而田口法只需进行52=25次实验,大大缩短了设计周期。

在建立正交实验矩阵后先对不同组合结果进行有限元求解得到正交实验表,为了分析各参数不同水平值对目标的影响以及所占的影响比重,首先对正交实验表中得到的结果进行平均值计算,如式(2)所示

(2)

式中n为实验次数；mi为第i次实验时对应的某一优化目标的性能指标。结果如表4所示。

表4 目标性能的平均值

然后再计算每个参数在每个因子水平下的某一性能指标的平均值。如计算开槽宽度w在水平1下的转矩T的平均值,其计算公式如下

mT(w)=(T1+T2+T3+T4+T5)/5

(3)

式中T1～T5分别为开槽宽度w在水平1下进行的第1～5次实验的稳态转矩平均值。

不同参数在不同水平值下的平均值如图4所示。

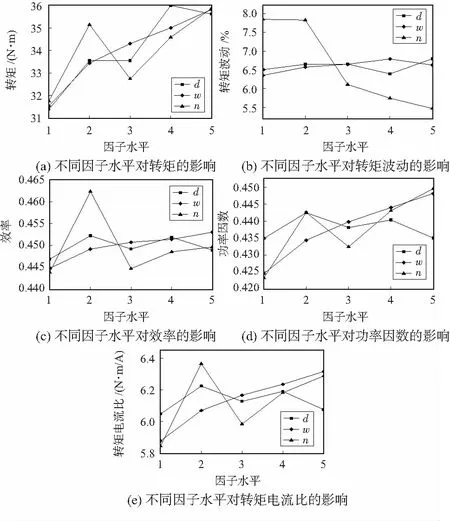
图4 不同影响因子水平对电机性能的影响

利用表4和图4所求得平均值以及不同水平值下各性能指标平均值,可计算各参数的改变对目标性能的影响比重,影响比重的占比结果见表5所示。

表5 参数对目标性能的影响比重 %

其比重的计算如式(4)所示

(4)

式中X为d，w，n等优化参数；SX为参数X下某一性能指标的方差值；mxi为参数X在水平i下对应的某一性能指标的平均值。

3.3 综合性能优化

通过表5的结果及综合分析可得,显然,参数d的改变对电机平均转矩的影响最大,参数w的改变对电机功率因数的影响最大,参数n的改变对电机转矩波动的影响最大。为了使2DoFDDIM的综合性能达到最优,参数d，w，n的选取分别应以最大平均转矩、最大功率因数以及最小转矩波动为标准,此时参数d，w，n的影响因子水平可以选取为4，5，5。

根据最终优化方案的各参数取值,建立该优化参数下的电机有限元模型并进行分析,电机优化前后的结果对比见表6所示。

表6 优化前后结果对比

由表6可以看出,经过选取不同的影响因子对旋转部分的综合性能进行优化与优化前相比,旋转转矩提高了20.4 %,转矩波动降低了22.0 %,效率和功率因数分别提高了1.6 %和8.4 %,转矩电流比则提高了10.2 %。

4 结 论

本文针对2DoFDDIM采用实心转子结构性能较低的问题,首先设计了一种在铸转子的周向和轴向开正交槽并在槽中嵌放铜条用以改善涡流回路从而实现电机性能改善的开槽铸铜转子结构；然后比较了电机的磁场和涡流分布情况,分析了电机性能得到提高的原因,同时建立了有限元模型对不同转子结构电机的特性进行计算与对比；最后对开槽铸铜转子的开槽参数采用田口法进一步优化选取,选取出了合理的参数,实现了电机性能的进一步提高。