基于人因差错的满布式支架安全评估研究

陈 实， 黄显周， 魏治国， 李俊德， 王鹏举

(云南云岭公路工程注册安全工程师事务所有限公司， 昆明 650021)

近年来，随着公路建设的快速发展，满布式支架因其形式多样、承载力要求低、成本较低等原因被广泛应用[1]，但支架施工发生事故的频率逐年增高，传统安全评估忽视了人因的主导作用。故亟需针对贯穿于支架施工始终的人因差错进行研究，使得支架施工安全评估向人因差错控制转变[2]。

目前，国内外对于支架安全人因差错的研究多集中于仿真、实测数据综合分析，Bruce等[3]针对混凝土构件施工进行了研究，利用事件树法得出各人为因素对结构可靠度的影响规律及偏离程度；谢楠等[4]通过对比分析大量事故数据，对支架施工过程中产生的人因差错进行了归纳分类；Fabian C Hadipriono等[5]分析了公路满布式支架倒塌事故的成因，利用层次分析法评估人因差错与事故发生概率的相关性；宋方方[6]结合近年来的模板支架倒塌事故数据，并采用事故树法进行人因差错识别。

综上，本文以满布式支架施工中的各类人因差错为主要研究对象，通过仿真模拟及多元回归等方法进行评估，以求基于人因差错对满布式支架施工全过程进行安全评估。

1 人因差错识别及分析

1.1 人因差错识别

通过搜集应急管理部近15年来的事故报表及相关文献报道，统计到152组较为典型的满布式支架事故，事故主因及其占比如表1所示[7]。

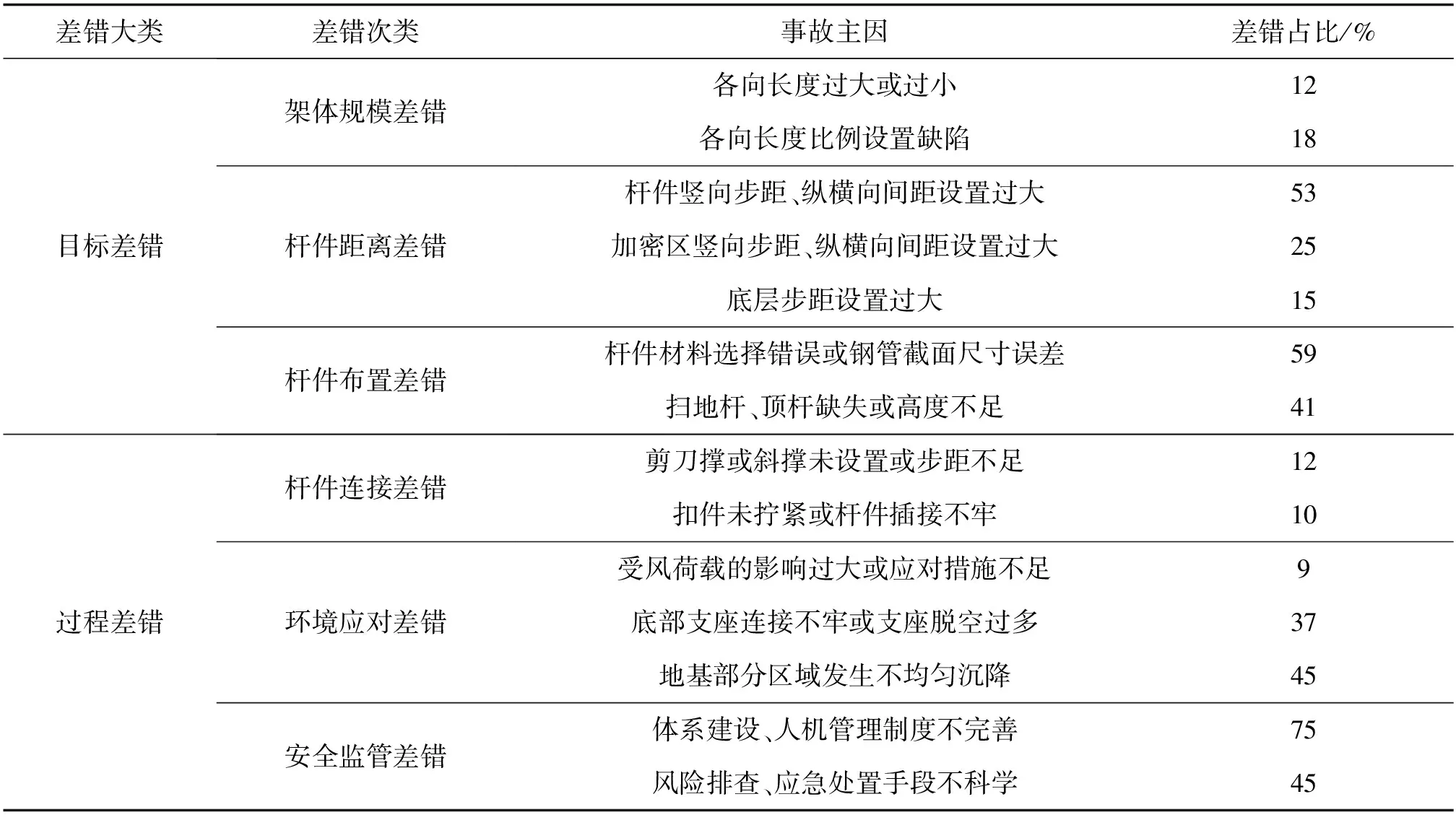
表1 事故数据分析

由表1可以看出，由人因差错导致的安全事故占比较大(最高达到75%)、类型较多(共6个次类，14个小类)，且存在多因素共同作用的现象，故本文将人因差错视为各类事故发生的主因进行研究。将其分为2类：目标差错(由于施工人员识图误差、实际测量误差、作业疏忽等原因而导致施工效果与最初设计要求产生偏离)、过程差错(作业过程中出现作业手段、施工工艺等误差而导致的过程不规范，从而使结果偏离期望值)。

1.2 人因差错指标体系构建

依据上述分类并结合工程实际参数，在Midas模型标准参数的基础上，按照模数或级数改变各类差错值，分析搭设阶段、浇筑阶段满布式支架的承载力及结构稳定性。

由于支架施工各阶段的差异，设置2种工况：工况1依据梁体浇筑时的实际情况进行模拟，选择支架自重和上部荷载；工况2依据支架搭设阶段的实际情况进行模拟，选择支架自重和风荷载。由于人因差错难以定量的特点，利用Matlab建立数集随机选择沉降区域、脱空区域等以模拟人的作用；利用专家及管理人员赋分来计算安全监管参数，各类人因差错的指标体系构建如表2所示。

1.3 人因差错分析

对表2中给出每类指标的6组参数值进行Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ相应的分级，其中各向长度差错、杆件步距(加密区)差错等2类变化程度最明显的目标差错分析结果如图1、图2所示。

通过分析仿真数据中的变化点、极限点，得出以下结论：

1) 人因差错与其他客观因素相比受环境影响较大，工况2(风荷载作用下)时人为造成的各向长度改变会使支架承载力骤降。

2) 支架杆件步距小于2.0 m时，可采取局部加密的措施以应对杆件间距类人因差错。

3) 人因差错造成的扫地杆高度大于0.7 m、立杆伸出长度大于0.2 m，会使结构处于不安全状态。

斜撑间隔差错、区域沉降差错等2类变化程度最明显的过程差错的分析结果如图3、图4所示。

通过分析仿真数据中的变化点、极限点，得出以下结论：

1) 人因差错出现在纵向剪刀撑设置时对结构的影响可忽略，故支架在纵向每10步设置剪刀撑更为经济安全，而斜撑必须按照规范要求满布。

2) 支架搭设时应提前检查地基、设置垫板，以防止人为带来的区域沉降差错导致底部失稳。

3) 支架的极限荷载值随着风荷载的增大呈线形增长，故严禁在风力等级较大时施工。

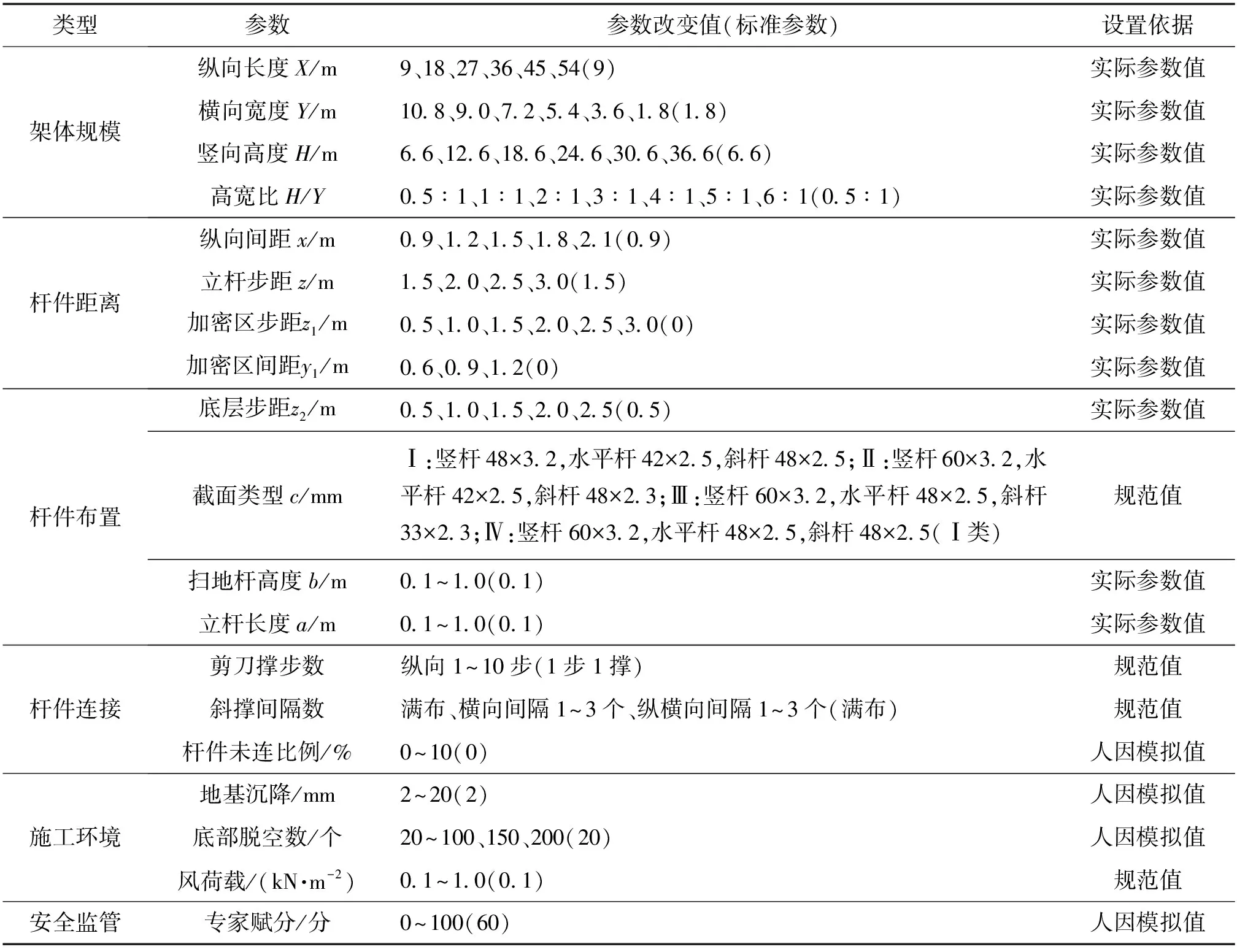
表2 人因差错指标体系

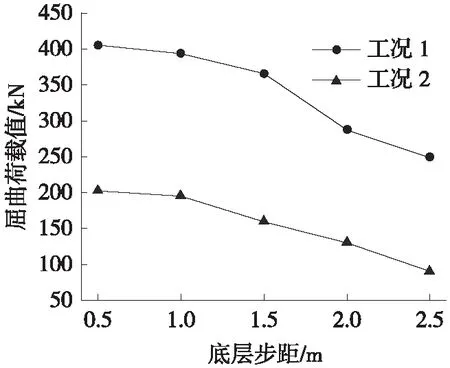
图1 屈曲荷载值随各向长度变化情况

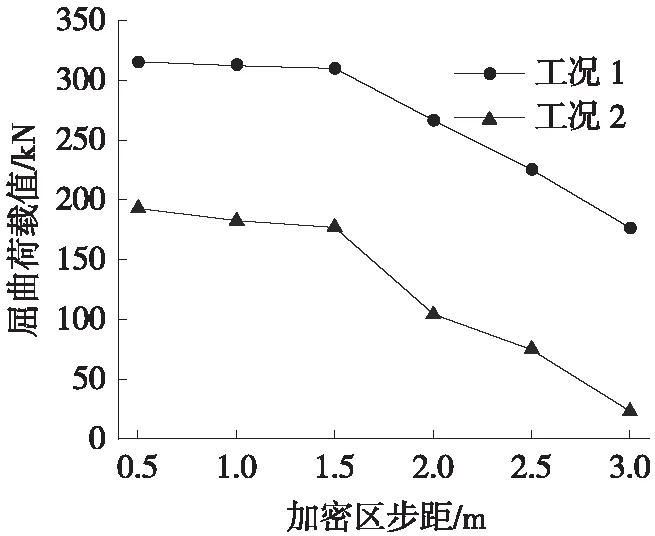
图2 屈曲荷载值随加密区步距变化情况

2 人因差错评估方法及分级

利用前文仿真屈曲荷载值数据及变化曲线拐点、极限点，结合工程实际情况对各类差错参数的影响程度、发生概率及产生后果进行综合评估。

2.1 人因差错影响程度评估

利用R语言程序中内置的kappa函数，针对搭设阶段(工况2)时的11个自变量、浇筑阶段(工况1)时的17个自变量进行共线性检验，结果如图5所示。

结果显示杆件间距(加密区)y1与杆件步距(加密区)z1相关性显著，这是由于加密区布置时各向距离需同时变化，去除杆件间距(加密区)y1后结果显示已不存在共线性，如图6所示。

图3 屈曲荷载值随斜撑间隔变化情况

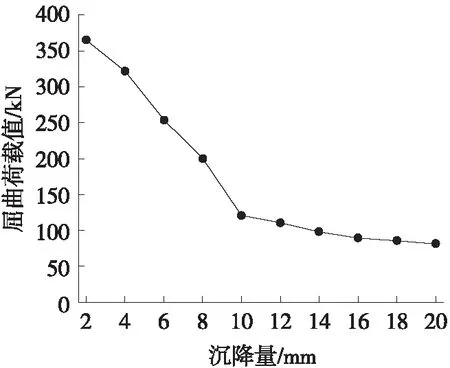
图4 屈曲荷载值随区域沉降量变化情况

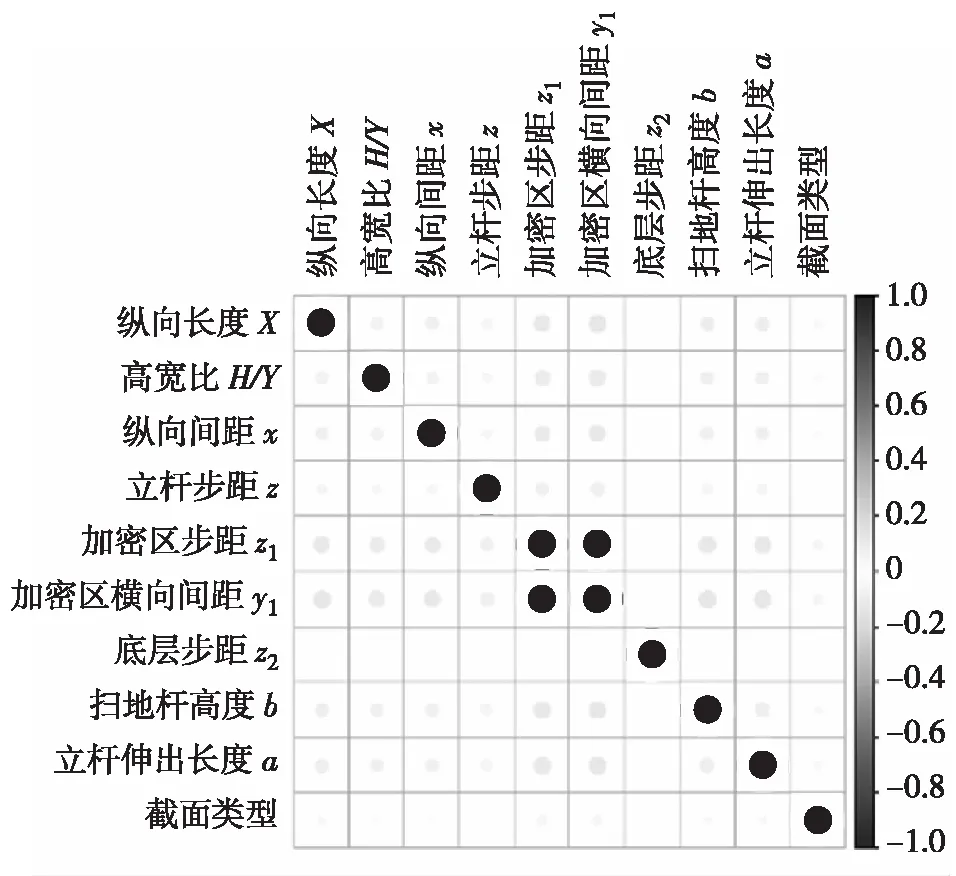
图5 原始共线性检验

将数据分为训练集、验证集及测试集，采用LASSO回归模型进行分析并交叉验证，结果如图7、图8所示。

最终通过回归分析得到支架2个阶段的承载力评估模型如下：

图6 优化后的共线性检验

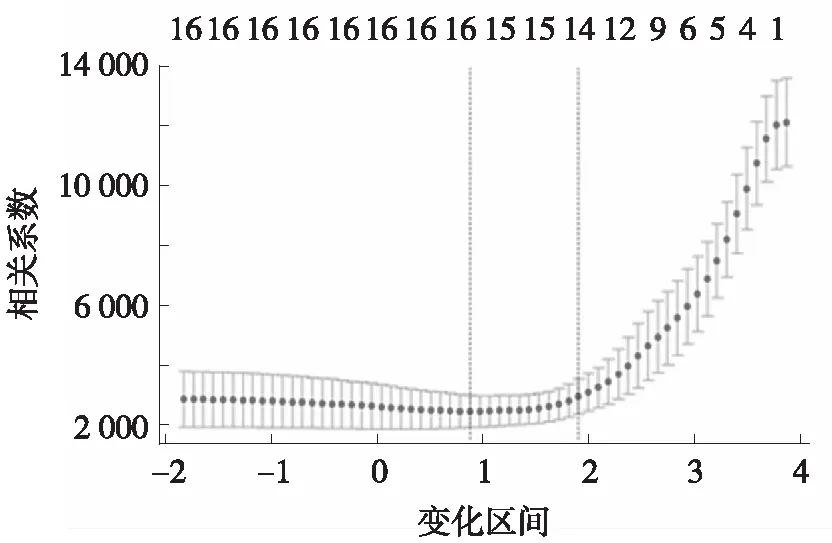
图7 LASSO回归模型分析

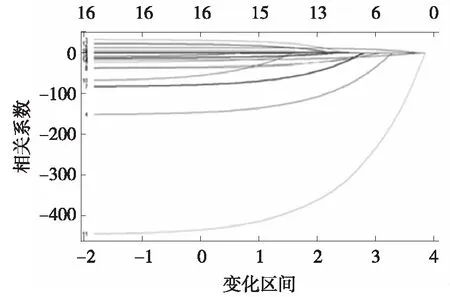
图8 测试集数据交叉验证

P1=1.731X-5.291H/Y+1.648x-6.018z-4.728z1-3.353z2+5.037m-1.751n-11.078a+1.404c-2.758α1-10.060α2-10.178α3+3.887 8α4

P2=0.216X-7.777H/Y-4.088x-5.319z-5.299z1-2.997z2-2.126b-9.011a-0.465c

通过将屈曲荷载值与规范中的可靠度指标β两两对应进行分级，结果如表3所示。

表3 影响程度分级

2.2 人因差错发生概率评估

利用肯特指数法—层次分析法进行层次划分，邀请桥梁施工专家进行赋分，对各因素构建两两判断矩阵确定权重，计算得到出概率分值P后根据表4确定事故概率等级。

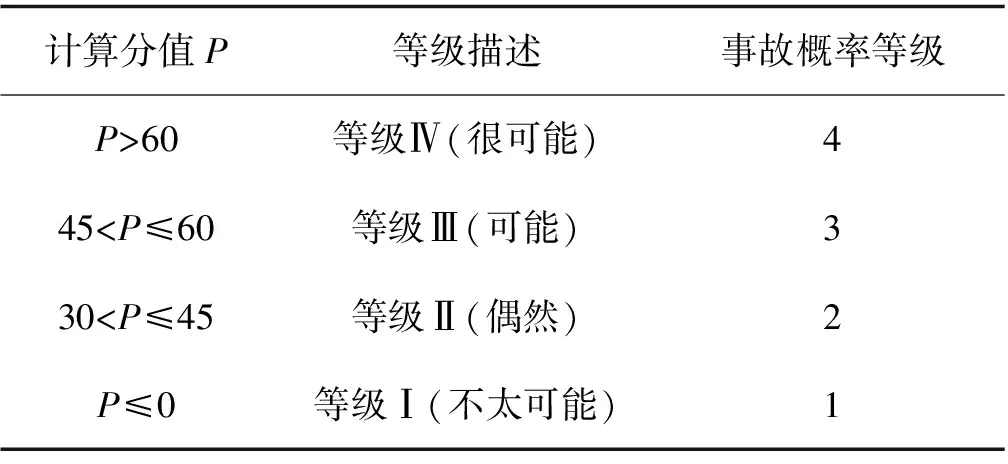
表4 事故概率分级

2.3 人因差错产生后果评估

根据人因差错后果表现形式的不同，将其分为经济损失(包括直接经济损失及间接经济损失)和非经济损失(包括生命损失、环境损失及社会损失)2大类，并建立人因差错后果估计总体模型：

C=Cz+Cj+Cm+Ch+Cs

式中：C为总后果；Cz、Cj为直接、间接经济损失；Cm为生命损失；Ch为环境损失；Cs为社会损失。为避免难以量化的后果计算带来误差，本文利用当量转换法进行分级，如表5所示[8]。

表5 事故后果分级

2.4 基于人因差错的评估分级

结合上述3个方面的评估方法，并取满布式支架安全影响程度评估等级与概率评估等级二者中大者，采用风险矩阵法确定满布式支架全过程安全评估等级，如表6所示。

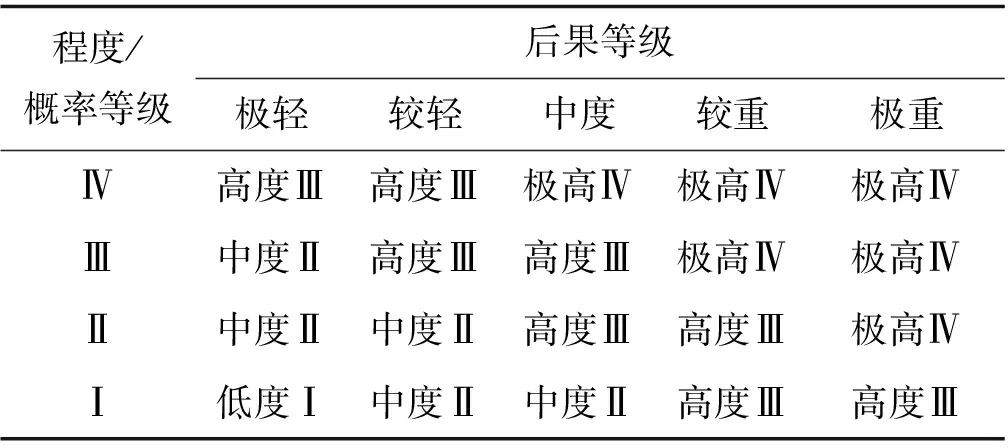
表6 施工安全分级

3 工程实例验证

3.1 工程概况

依托宜宾至昭通高速公路云南段一期项目，针对彝良(海子)至昭通A1段北闸互通F匝道桥第4联现浇箱梁开展安全评估[9]。该专项工程采用承插型盘扣满布式支架，各参数调查结果如表7所示。

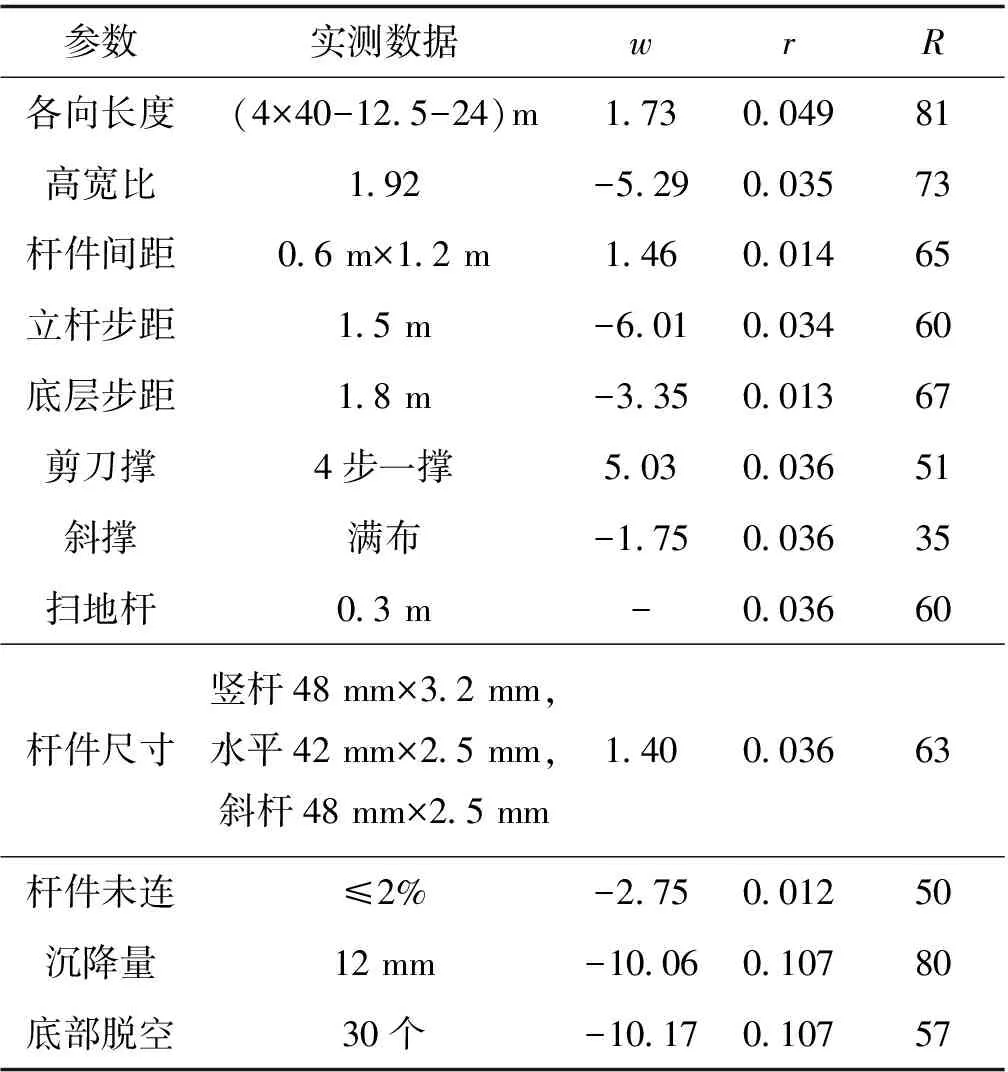
表7 实际参数调查

3.2 安全评估

利用前文所述评估模型计算可得，该支架专项工程的安全评估等级为Ⅲ级(高度风险)。邀请专家利用传统打分法(不以人因作主导，以整体安全为导向)得出该工程的安全等级为Ⅱ级(中度风险)，说明本文建立的人因差错概率评估模型与实际工程较为符合，且更加符合施工安全要求[10]。

3.3 结果验证

将有限元分析所得的屈曲荷载值，与前文所得的承载力评估模型计算值进行对比，发现承载力模型评估值误差均在10%以内，且结果更符合实际，二者结果对比如表8所示。

表8 影响程度评估对比

4 结论

本文利用有限元软件模拟、数据分析等手段并结合工程实践，对满布式支架人因差错的影响程度、发生概率、产生后果及安全评估等问题展开了研究，并得出以下认识：

1) 结合事故数据分析，发现支架施工中的人因差错是导致事故发生的主导因素，利用仿真软件得出了各类人因差错的产生机理及作用规律，最终构建出基于人因差错的支架施工安全评估指标体系。

2) 研究得出人因差错的影响程度评估模型、发生概率评估模型、产生后果评估模型多维评价方法并进行分级，应用于云南省高速公路项目后发现影响程度评估误差在10%以内、发生概率评估等级更加贴近实际，说明模型具有可行性及实用性。

3) 未来对于支架施工安全的研究需要开发相关的系统，通过电脑终端、移动设备和互联网，与智能感应设备、信号传输设备结合从而开发智能物联网系统。