PC连续梁应力水平与长期变形特性
魏汉锋,黄 劲
(1.广东省高速公路发展股份有限公司佛开分公司,广东 佛山 528051;2.广东华路交通科技有限公司,广州 510420)
0 引言
大跨度PC连续梁以其施工简便、造价经济、行车舒适等特点,在公路建设中得到了广泛应用。然而,近年来,PC连续梁主跨的持续下挠、腹板斜裂缝、底板开裂等现象频繁出现,已成为困扰国内外同类桥型设计、施工及养护的主要问题[1-3]。
大跨径预应力混凝土梁桥长期过量下挠的问题,究其原因主要是对混凝土材料的徐变收缩预测不足,以及长期预应力损失估计偏低等原因[4]。为分析这一问题,国内外进行了相关预应力混凝土梁长期性能的试验研究[5-7],但试验所采用的预应力混凝土梁模型尺寸小且设计应力水平较低,与目前运营的大跨径预应力混凝土梁桥实际的高应力状态不相符。
基于此,在已有研究成果的基础上[8-9],本文通过建立高应力状态下的梁体试验模型,对梁体长期变形与应力状态的关系以及不同应力状态下的梁体徐变变形进行试验研究。设计了高“应力/强度”比值下的PC连续试验梁,根据连续梁受力状态选取跨中截面和中支点截面为试验的关键截面,分析了试验梁的预应力损失、跨中截面上缘总应变及徐变应变、中支点截面下缘总应变及徐变应变随时间的发展规律,并与现行规范的理论计算值进行了比较。同时分析关键截面应力水平,上、下缘应力差对试验梁长期性能参数的影响规律,有利于进一步深入了解梁体徐变对大跨径桥梁长期变形的影响,为准确预测大跨度预应力混凝土梁桥的长期变形提供理论基础。
1 试验方案
1.1 试验梁
试验共设计了4片连续试验梁,采用矩形截面,其截面几何尺寸为18cm×22cm,长度为3.8m,计算跨径为1.8m。梁体中配置φs15.2低松弛预应力钢绞线,试验中通过调整钢绞线的锚下张拉力来控制混凝土梁截面的应力状态。
由于梁体的应力水平越高,上、下缘应力差越大,则梁体徐变及长期变形越大[10]。试验中,4片连续试验梁的应力水平各不相同,当分析梁体上缘应力水平对跨中长期变形的影响时,需保持梁体上、下缘应力差基本相同,分为2组:AA组(PCC1、PCC3)、BB组(PCC2、PCC4)。当分析梁体上、下缘应力差对跨中长期变形的影响时,需保持梁体上缘应力水平基本相同,分为2组:CC组(PCC1、PCC2)、DD组(PCC3、PCC4)。
表1为各试验梁的关键截面初始应力状态、单股预应力钢束张拉力及跨中的集中荷载布置。
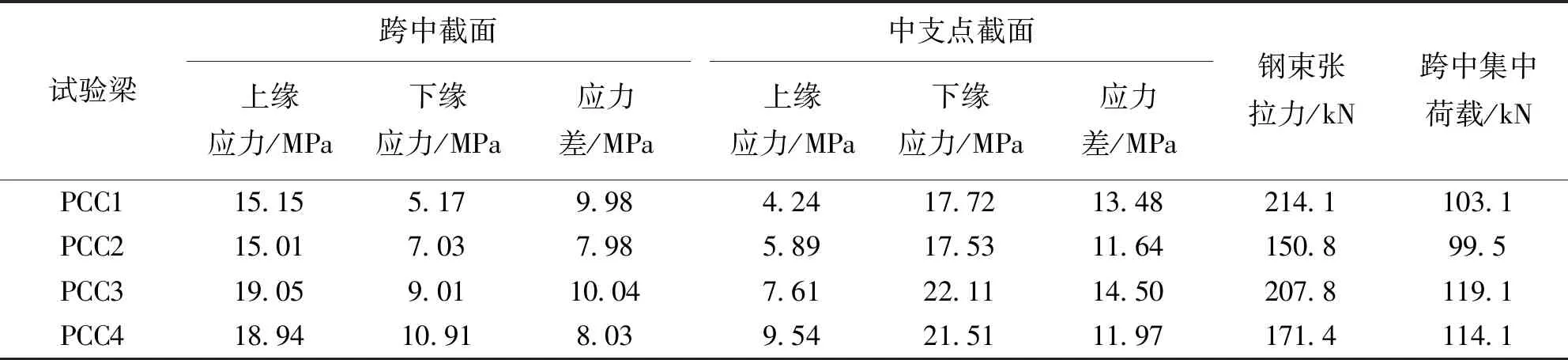
表1 各试验梁关键截面初始应力状态、单股预应力钢束张拉力及跨中的集中荷载布置
1.2 试验梁的加载方式
为了使试验梁达到较高的应力状态,同时避免加载系统出现卸载现象,试验利用杠杆原理,通过地锚进行加载。如图1所示,其中F1为压重块重量,F2为施加在试验梁上的集中荷载,F3为固定端位置所承受的力。设计支座的加载装置如图2所示。根据杠杆原理可以得出施加在试验梁跨中截面上缘的集中荷载F2的公式:

图1 试验梁加载

图2 PC连续试验梁加载装置
1.3 试验梁的测点布置
试验中,应力是通过应变的测量来实现的,选取试验梁跨中及中支点截面上、下缘布置应变传感器。此外,为观测试验梁长期变形情况,选取跨中截面下缘布置位移测点,图3所示为测点布置。
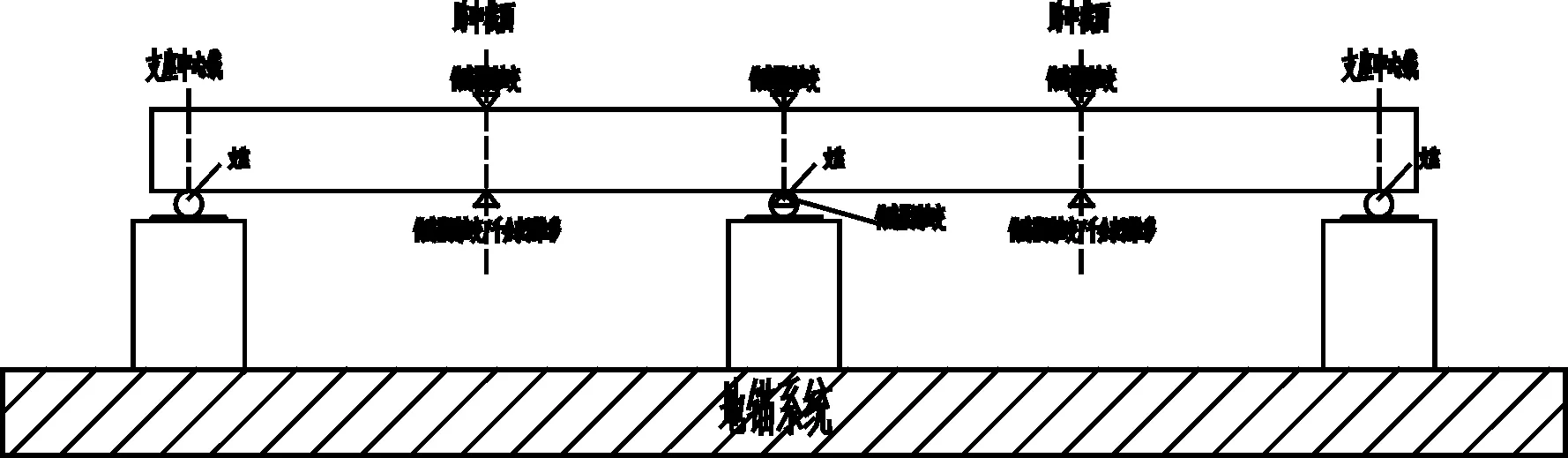
图3 应变、位移测点布置
1.4 试验加载流程
试验前期准备工作完成后,即可布置数据采集系统、安装加载设备,并进行初读数。
初读数完成后,采用预应力钢束张拉和跨中集中荷载同时施加的方式对试验梁进行加载,并分级逐步加载。施加跨中集中荷载时,试验梁的两跨应先后逐步施加。
试验梁张拉加载前后,均需测定预应力锚固损失、锚固后预应力及1/4和3/4点处集中荷载、跨中及中支点截面上、下缘应力初始值,随后定期采集上述数据,并进行分析。
2 试验数据分析
2.1 预应力损失
后张法构件传力锚固后的预应力损失主要由预应力钢束的应力松弛和梁体混凝土收缩徐变引起。通过压力传感器对试验梁钢束的预加力损失进行测定,钢束的预加力随时间的变化历程如图4所示。

图4 预应力钢束张拉力测试结果
从图4可以看出:随着时间的增加,钢束的预加力不断减小,前10d内预加力损失较快,后期损失发展趋于平缓,这主要是由于前期钢束的松弛及徐变效应发展较快引起的。相对于张拉锚固后的预加力大小,140d时的预应力损失分别为6.19%、7.83%、7.30%、7.04%。
表2列出了各试验梁的预应力损失比例(相对于张拉锚固后的初始预应力大小)。可以看出:相对于140d时的预应力损失,20d的预应力损失分别达到了总预应力损失的62%,60d的预应力损失分别达到了总预应力损失的74%,100d的预应力损失分别达到了总预应力损失的88%。
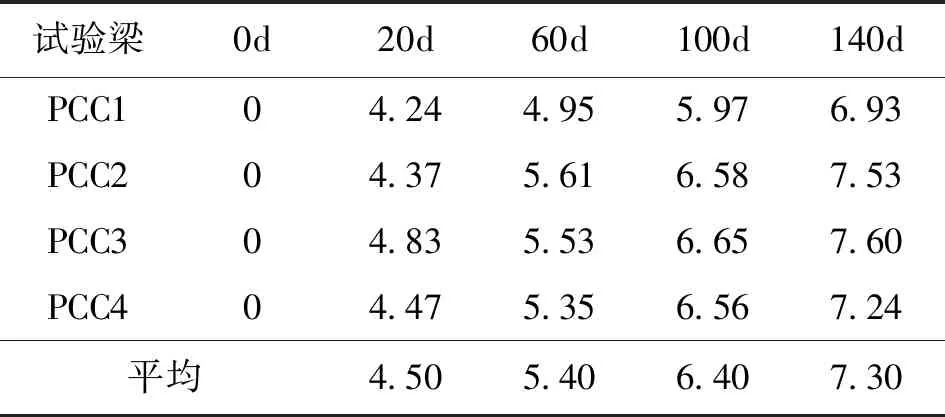
表2 连续试验梁预应力损失比例 (单位:%)
通过与规范[11]计算值比较可知:各片连续试验梁的实测预应力损失均较规范计算值大,张拉锚固后140d时,各片连续试验梁预应力损失实测值与规范计算值的比值分别为1.25、1.20、1.17、1.22。
2.2 总应变与应力分析
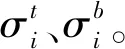
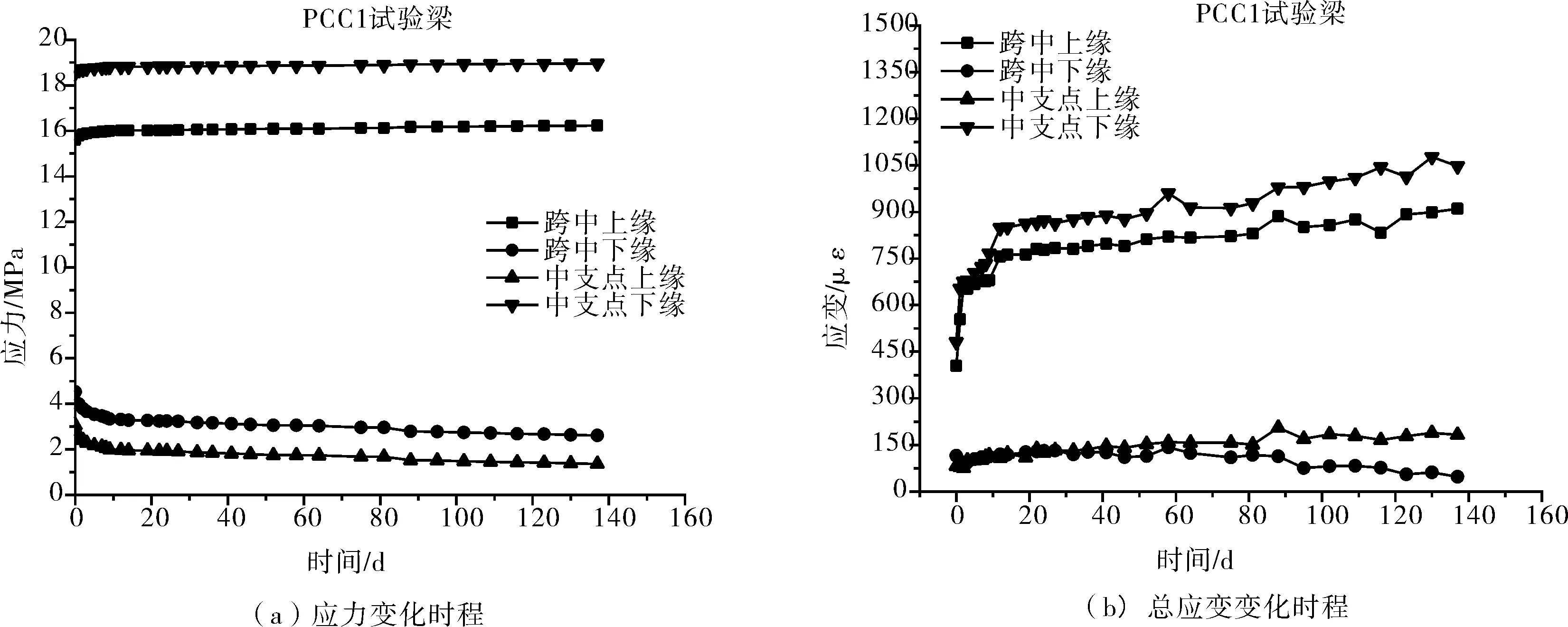
图5 PCC1连续试验梁应力与总应变变化时程
由图5(a)可以看出,跨中截面上缘和中支点截面下缘的应力均随着时间的发展不断增加,且张拉锚固后前10d内相对增加的速率较快,而10d后相对增加的速率趋于平缓;各试验梁跨中截面下缘和中支点截面上缘的应力则呈现相反的变化趋势,从而导致截面上、下缘的应力差不断增加。由于结构自重和外荷载未发生改变,产生这种截面应力变化的原因主要是由于钢束预应力损失引起的。同时,预应力钢束的松弛和混凝土徐变效应在试验前期发展相对较快,从而导致跨中截面下缘应力及上、下缘应力差在试验前期较快地发展。
对比总应变的变化时程可以看出,应力状态越高,总应变变化就越明显,而混凝土徐变产生的应变,不会导致应力的增加。
表3为张拉锚固后140d内各连续试验梁跨中截面上缘和中支点截面下缘总应变随时间的增加值。可知:前期总应变增加较快,而随着时间的发展总应变的增加趋于平缓;张拉锚固后30d时,各试验梁跨中截面上缘的总应变增加值占140d内该跨中截面上缘总应变增加值的比例分别为74.5%、68.5%、68.8%、68.5%;张拉锚固100d时,该比例分别为89.6%、87.9%、85.7%、85.3%;张拉锚固后30d时,各试验梁中支点截面下缘的总应变增加值占140d内该截面下缘总应变增加值的比例分别为69.7%、78.9%、73.5%、78.3%;张拉锚固100d时,该比例分别为91.3%、85.7%、89.0%、91.6%。
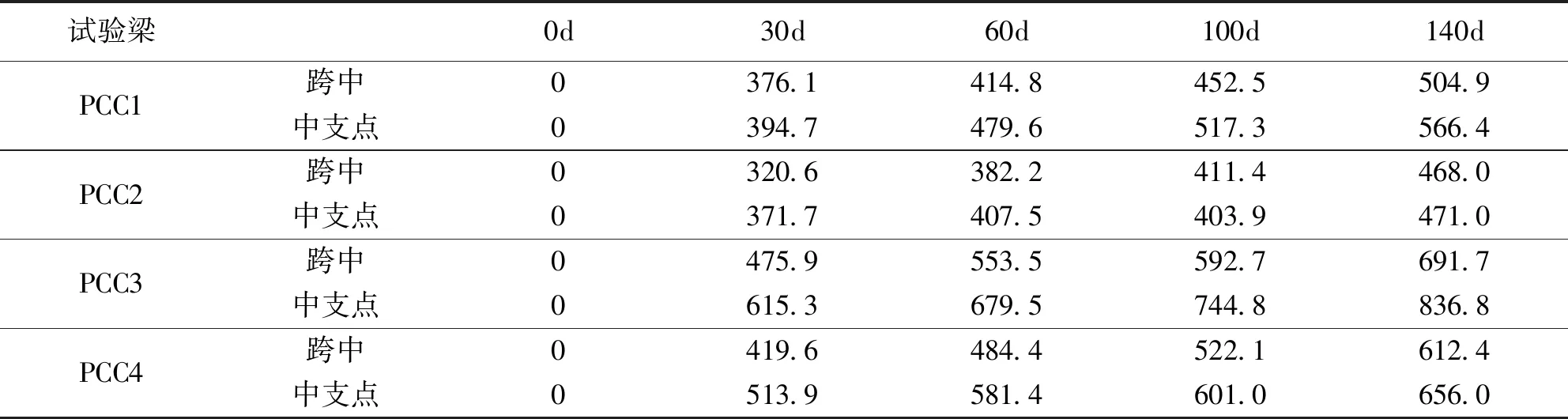
表3 连续试验梁总应变增加值 (单位:με)
表4列出了各连续试验梁跨中截面上缘与中支点截面下缘实测总应变与规范[11]计算值之间的差值。由表4可见,实测总应变均大于规范计算的总应变。
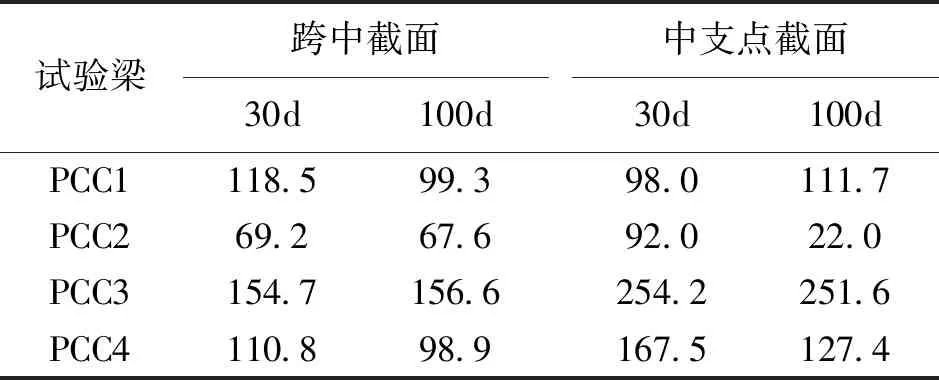
表4 连续试验梁实测总应变与规范计算值的差值 (单位:με)
各试验梁跨中截面上缘与中支点截面下缘实测总应变均较规范计算值大,主要是混凝土徐变应变的差异。
2.3 徐变应变分析
图6为PCC1连续试验梁跨中截面上缘及中支点截面下缘的徐变应变实测值与规范计算值之间的比较,其他试验梁呈现出相似的变化规律。
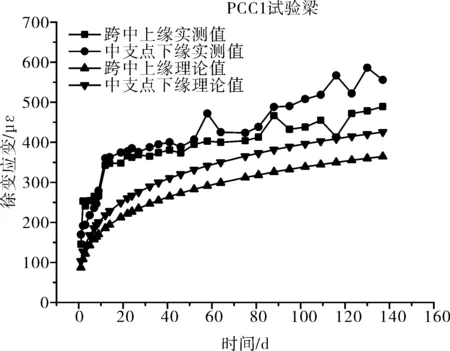
图6 PCC1连续试验梁实测徐变应变与规范计算值对比
从图6可以看出:跨中截面上缘及中支点截面下缘的实测徐变应变与规范计算的徐变应变均随着时间的发展不断增加,且试验前期徐变应变增加迅速,试验后期徐变应变增加平缓;各连续试验梁跨中截面上缘及中支点截面下缘的实测徐变应变均大于规范计算值;不同连续试验梁间相同截面的徐变应变不同,主要是由于各试验梁的应力水平不同所致,并且应力水平越高,上、下缘应力差越大,则该截面试验梁的徐变应变越大。
表5列出了各试验梁张拉锚固后不同时间段时跨中截面上缘及中支点截面下缘的实测徐变应变与规范计算值的比值,可以看出:各连续试验梁跨中截面上缘及中支点截面下缘的实测徐变应变与规范徐变应变值的比值均大于1.00,可见现行规范考虑的徐变效应偏小,不能够准确预测各试验梁的实测徐变应变。

表5 试验梁徐变应变实测值与规范计算值的比值
3 PC连续梁徐变与应力状态的耦合作用
3.1 应力状态对徐变的影响
通过试验梁的徐变应变实测数据可知,混凝土徐变性能与试验梁的应力状态密切相关:试验梁应力差保持基本相同时,徐变应变随着应力水平的增大而增大;试验梁应力水平保持基本相同时,徐变应变随着应力差的增大而增大。而规范[11]中徐变计算考虑的因素包括混凝土加载龄期、混凝土强度、混凝土构件理论厚度和年平均相对湿度。
任意时刻的徐变应变εcr和弹性应变εe,由徐变系数φ(t,t0)的定义,可得:
图7为试验梁跨中截面的实测徐变系数与规范徐变系数的比值。从图7可见,实测徐变系数均大于规范的徐变系数,且跨中截面上缘应力水平越大,跨中截面上、下缘应力差越大,则实测徐变系数越大。

图7 各试验梁跨中截面实测徐变系数
3.2 基于实测数据的徐变系数修正
通过3.1节分析可知,实测总应变、徐变应变和预应力损失均大于规范计算值,主要是由于规范对于高应力状态下混凝土徐变性能考虑不足导致。现行规范假定徐变系数与混凝土构件的应力状态无关,而试验中通过实测徐变系数验证了其与试验梁的应力水平的相关性,且随着试验梁应力水平增大,试验梁上、下缘应力差的增大,实测徐变徐系数与规范徐变系数的差值逐渐增大。因此,考虑修正衡量混凝土徐变性能的指标——徐变系数φ(t,t0)。
随着时间的增加,各试验梁的徐变系数均呈收敛趋势。选择指数函数和波尔兹曼函数对徐变系数进行修正,经过多次拟合及试算,最终的修正系数λ与混凝土上缘压应力σ以及时间t有关,如下式所示:
λ=f(σ,t)=[1.28+0.15e-0.09(t-t0)]·
式中:t为计算考虑时刻的混凝土龄期(d);t0为加载时的混凝土龄期(d);σ为试验梁上缘的压应力值(MPa)。
3.3 基于修正徐变系数的理论数据与实测数据的比较
3.3.1 徐变应变
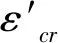
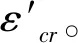
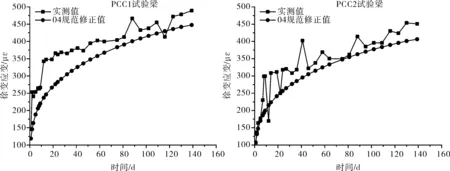
图8 连续试验梁跨中截面上缘实测与修正徐变应变
3.3.2 总应变
考虑修正系数λ后的总应变ε″计算公式:
ε″=εe+φ′(t,t0)·εe+εsh
图9绘出了各连续试验梁中支点截面下缘实测总应变ε′与考虑修正系数λ后的理论总应变ε″。从图9可见,修正后的总应变与实测总应变随时间的发展趋势保持一致,修正后的总应变与实测总应变能较好地吻合。
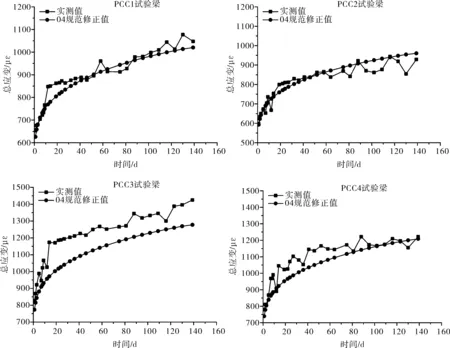
图9 连续试验梁中支点截面下缘实测与修正总应变
4 结论
针对影响预应力混凝土梁桥长期性能的各主要因素,包括混凝土的收缩、徐变特性以及预应力损失等,进行深入的试验研究。通过对不同应力状态下试验梁的长期变形研究,为准确预测大跨径预应力混凝土梁桥的长期变形提供试验支持,得到以下结论:
(1)根据试验数据,验证了在高应力状态下,结构受压总应变及徐变应变的实测值均大于规范计算值。当截面应力梯度(上、下缘应力差)保持基本相同时,预应力损失、受压总应变及徐变应变随着压应力水平的增大而增大;当压应力水平保持基本相同时,截面应力梯度越大跨中截面及中支点截面的上、下缘应力差越大则总应变及徐变应变越大。
(2)在高应力状态下,实测徐变系数均大于规范给定的徐变系数,且随着应力水平的提高,实测值与规范计算值差别越来越大,反映了混凝土徐变特性的非线性,应力水平越高,上、下缘应力差越大,则徐变系数越大。根据有限的试验数据分析,得到了与应力状态相关的徐变系数φ(t,t0)修正系数λ,考虑修正系数λ后的理论数据与试验实测数据能较好地吻合,其准确性还需更多试验进一步验证。
(3)当应力水平σ/fck小于40%时,可采用规范推荐的线性徐变理论计算;而应力水平超过此范围,则应充分考虑混凝土徐变的非线性。建议通过试验得到高应力状态下的混凝土徐变系数,从而更准确地预测预应力混凝土梁桥的长期变形和长期应力,保证桥梁的安全和正常使用性能。

