k法和变k法在常用级配设计中的应用

陈其红

(广东省高速公路有限公司粤赣分公司，广东 河源 517000)

0 引言

在我国公路建设快速发展的背景下，公路建造技术也在日益提高，如级配设计技术。伴随公路建设过程的推进，沥青混合料级配设计理念也在日益更新。以广东省为例，早些年AK级配和AC级配应用较多，经过多年实践经验的积累后，发展到目前应用较多的GAC级配。此外，SMA和Novachip等级配在很多公路中也得到了成功应用。

关于级配设计方法已有较多研究成果。贝雷法通过控制粗集料与细集料关键筛孔尺寸的通过百分率比例关系，使沥青混合料的矿料级配具有较好的骨架结构[1]；沙庆林[2]建立了多碎石沥青混凝土SAC系列级配，提出了整套级配的计算方法；张肖宁[3]建立了沥青混合料组成设计主骨料填充法 CAVF法，提出了粗、细集料组成的计算公式；刘慧[4]在现有级配的基础上，提出了嵌挤骨架型沥青混合料的设计方法；侯剑楠[5]通过设计非标准的贯入试验，基于不同粒径集料贯入试验的强度差异，提出了沥青混合料级配设计方法；赵永利[6]、李文良[7]借鉴土工CBR试验方法，通过贯入强度的大小和不同粒径集料的合成孔隙率，来确定各档的掺配比例；刘克[8]将集料的混合机制量化为填充、干涉、取代和壁效应4种，在此基础上，提出了二元混合矿料间隙率填充取代复合模型。

本文从级配理论的发展历程着手，通过k法和变k法，对广东省常见的五种级配进行对比分析和总结，以期找到级配发展过程中的共性和特性，丰富现有的矿料级配理论，为级配的设计提供参考和建议。

1 级配理论的发展历程

1.1 W.B.FULLER曲线

W.B.Fuller曲线，即最大密度曲线。表达式：

(1)

式中:Px为粒径d集料的通过百分率(%)；D为集料的最大粒径(mm)。

1.2 A.N.TALBOL公式

A.N.Talbol公式，即n法。表达式：

(2)

式中：Px为粒径d集料的通过百分率(%)；D为集料的最大粒径(mm)。

Talbol公式在n=0.5时，即为Fuller曲线。

1.3 同济大学林绣贤提出的I法

表达式：

Px=100(i)x

(3)

(4)

式中：i和n的取值关系见表1。

表1 i和n的取值关系

根据实践经验，认为i=0.7～0.8是合理的范围。i>0.8细料太多；i<0.7细料太少，容易透水；i=0.75是最佳组成。这与n法认为的0.5～0.3为合理范围和日本认为n=0.35～0.45与实际最为接近，结论是一致的。

i法和n法的缺点：因它是无穷级数，没有最小粒径的控制，因而用于粒料级配的面层和基层尚可。如用于沥青混合料组成，往往造成矿粉含量过高，使得路面高温稳定性不足。因此，苏联控制筛余量递减系数k的方法，克服了这个缺点。

1.4 苏联提出的k法

表达式：

(5)

(6)

(7)

式中：Px为粒径d集料的通过百分率。

从以上发展的过程中，可以看出k法是较完善的连续级配的组成计算法。

1.5 变k法

上述4种方法都是连续级配设计方法，组成连续级配的曲线平滑圆顺，相邻颗粒间有一定的重量比例，不容易离析。但按照连续级配设计的沥青混合料面层的摩阻系数很难保证，为了提高面层或磨耗层的摩阻系数及高温稳定性，提出了粗骨料基本靠拢，摩阻系数大，高温时模量不太低，低温时模量不太高。由此，便形成了变k法。

变k法的计算思路：(1)某一级以后的细料k1不变，保证一定的密实度，而前几级的k2取稍小值，保证粗骨料基本靠拢。这样可以得到密实度高、粗骨料嵌挤的级配组成，也是通常说的骨架密实型级配。如k1=0.75，k2=0.65。(2)当计算上限和下限时，分类检验。计算上限时，计算式中的系数按100；计算下限时，计算式中的系数按90。计算平均值时，系数按95。

计算流程：

(1)根据矿料最大公称粒径确定粗集料与细集料的筛孔界限，本文以AC-20说明，筛孔界限为4.75mm。

(2)计算n值。按(式5)～(式7)计算4.75mm筛孔尺寸以上的n值和Px。

(3)按(式5)～(式7)计算4.75mm筛孔尺寸以下的n值和Px。

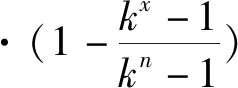
2 方案设计

选取AK-16、AC-16、GAC-16、SMA-16及novachip B型五种级配，原则是选取沥青面层常用的主要级配类型。采用横向对比和纵向对比的方法,采用k法、变k法分别进行级配范围、级配中值的横向对比，以期掌握或得到级配设计理念在常见级配上的体现性或对应关系。通过五种级配对应关系的纵向对比，分析级配设计的思路与变化；并结合各种级配的应用情况，给出一些通用性的结论或级配优化方向。具体步骤：

(1)分别采用k法计算五种级配的范围，k取不同的值进行试算，分别与规范的级配范围进行比较，确定落在规范级配范围内的k的取值。

在该步骤中，级配上限的系数取100，级配下限的系数根据原级配选取，AK-16、AC-16、GAC-16、SMA-16及novachip B型分别取90、90、95、90和85。另需说明的是，最大粒径D是指大于它的重量比不得超过5%的定义，因此，公式中的D为最大粒径，而非最大公称粒径。

(2)若k取某个或某几个值时，采用k法得到的级配范围全部在规范要求的级配范围内，不再采用变k法计算，记录k的取值或k值组成的区间；若无论k如何取值，采用k法得到的级配范围始终不能落在规范要求的级配范围内，便以4.75mm为分界点，分别对比采用k法计算的4.75mm以上部分与规范的对应情况。

(3)确定采用k法计算的4.75mm以上的能落在规范要求的级配范围区间之内的k值或k值区间；在该值下，再次采取k法计算级配中值，然后将4.75mm以下的通过变k法进行试算，直至全部落在规范要求的范围内为止，记录k的取值或k值组成的区间。需要说明的是，AK-16、AC-16、GAC-16、SMA-16及novachip B型4.75mm以上部分级配中值的系数分别取95、95、97.5、95和92.5，而4.75mm以下部分级配中值的系数为采用k法计算得到的4.75的通过率。

(4)若第三步始终不能落在规范要求的范围内，表明采用k法和变k法均设计不出该级配。

3 k法和变k法在五种常用级配中的体现

3.1 AK-16

按照1.4节和1.5节的计算公式，将采用k法计算的级配与AK-16级配进行比较，见表2。

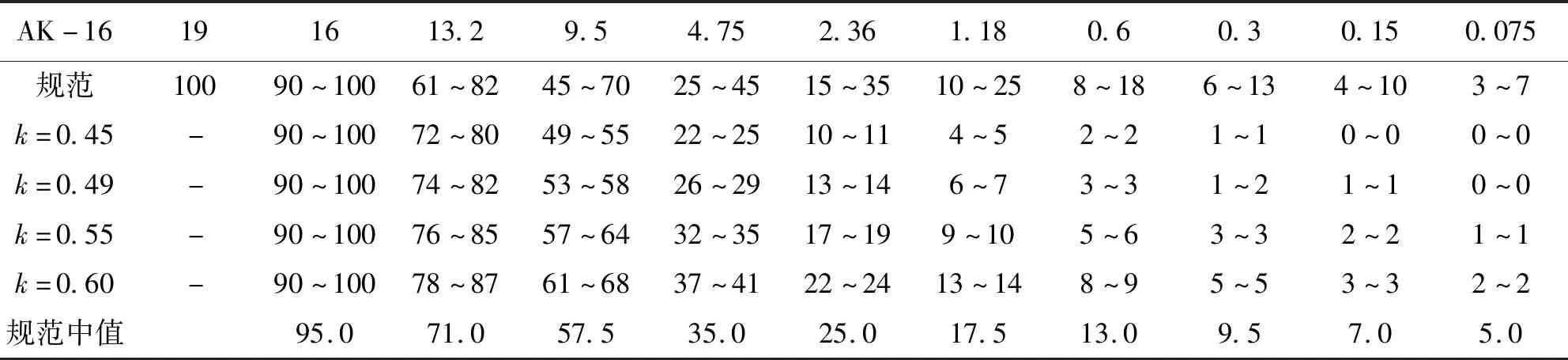
表2 AK-16与k法计算的级配范围比较

由表2可见，按照k法计算的级配范围与规范给出的AK-16级配范围有较大差异，除了当k=0.49时，按照k法计算的4.75mm以上的级配范围在规范范围内，其他的k值均不在规范的级配范围内；按照k法计算的4.75mm以下的级配范围均不在规范范围内。

因此，采用变k法进行计算和分析。4.75mm以上的k值仍取0.49，但因计算的是级配中值，系数选取95%；而4.75mm以下的按变k法进行试算，系数取为4.75mm的通过率，为27%。计算结果见表3，当k=0.8时，与中值最为接近。

表3 AK-16级配中值与变k法计算的级配中值比较

3.2 AC-16

按照1.4节和1.5节的计算公式，将采用k法计算的级配与AC-16级配进行比较，见表4。

由表4可见，在k取0.70和0.75时，各档筛孔的计算级配范围均在规范要求的级配范围内，因此确定该k值区间为0.70～0.75；k=0.70时，计算的各档筛孔通过率与规范中线基本一致。可以看出，AC-16级配可以很好地由k法来表达和解释。

表4 AC-16与k法计算的级配比较

3.3 GAC-16

按照1.4节和1.5节的计算公式，将采用k法计算的级配与GAC-16级配进行比较，见表5。

表5 GAC-16与k法计算的级配比较

由表5可见：按照k法计算的级配范围与规范给出的GAC-16级配范围有较大差异，k法不能直接计算得到GAC-16的级配。

k取较小值(k=0.50和0.55)计算的4.75mm以上部分级配范围能落在规范给出的级配范围内，k取较大值(k=0.70)计算的4.75mm以下部分级配范围能落在规范给出的级配范围内。

因此，采用变k法进行计算和分析。同AK-16系数取值方法，如表6所示，4.75mm以上、以下部分的k值分别取0.55和0.80时，计算得到的级配与规范中值较为接近。

表6 GAC-16级配中值与变k法计算的级配中值比较

3.4 SMA-16

按照1.4节和1.5节的计算公式，将采用k法计算级配与SMA-16级配进行比较，见表7。

表7 SMA-16与k法计算的级配比较

由表7可见：按照k法计算的级配范围与规范给出的SMA-16级配范围有较大差异，k法不能直接计算得到SMA-16的级配。仅当k值取0.45和0.50时，计算的4.75mm以上部分级配范围能落在规范给出的级配范围内，因此，k值区间取0.45～0.50。

因此，采用变k法进行计算和分析。同AK-16、SMA-16系数取值方法，如表8所示，4.75mm以上、以下部分的k值分别取0.45和0.95时，计算得到级配与规范中值较为接近。

表8 GAC-16级配中值与变k法计算的级配中值比较

3.5 NOVACHIP B型

按照1.4节和1.5节的计算公式，将采用k法计算的级配与Novachip B型级配进行比较，见表9。

表9 Novachip B型与k法计算的级配比较

由表9可见：按照k法计算的级配范围与规范给出的Novachip B型级配范围有较大差异，k法不能直接计算得到Novachip B型的级配。仅当k值取0.35时，计算的4.75mm以上部分级配范围能落在规范给出的级配范围内，因此k值取0.35。

采用变k法进行计算和分析。同AK-16、SMA-16及GAC-16系数取值方法，如表10所示，4.75mm以上、以下部分的k值分别取0.35和0.80时，计算得到的级配与规范中值较为接近。

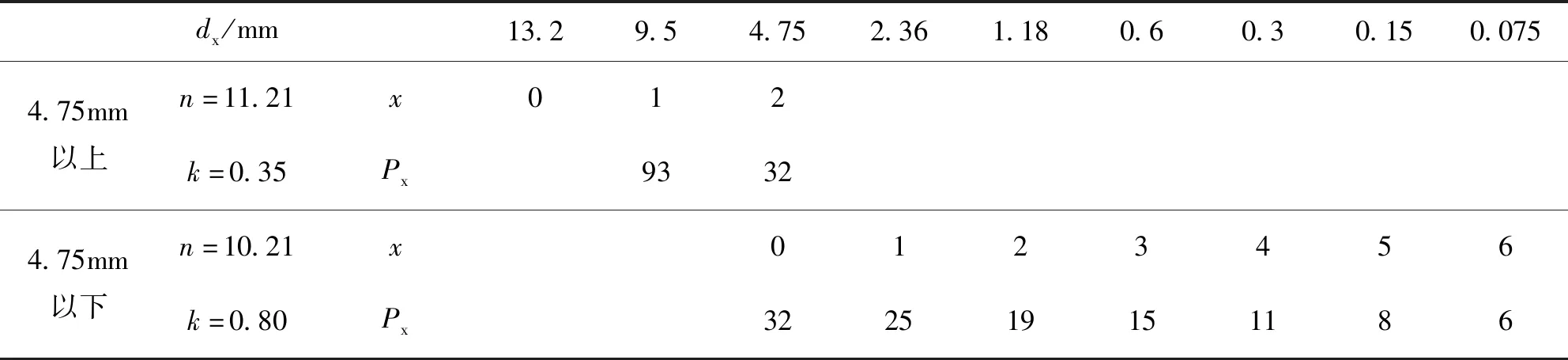
表10 Novachip B型级配中值与变k法计算的级配中值比较

3.6 对比分析

将上述五种级配采用k法或变k法计算的级配范围能落在规范范围内的k值或者k值区间汇总,见表11。将上述五种级配采用k法或变k法计算的级配中值与规范中值基本接近的k值汇总，见表12。

表11 级配范围k值或k值区间汇总

表12 级配中值对应的k值汇总

由表11和表12的汇总数据，结合k法和变k法的物理意义，可以得到：k的单独取值或取值区间能表述级配的嵌挤状态和密实程度。可直接通过k法表达的级配只有AC-16，表明AC-16是连续密级配，AC型级配设计理念重在形成较好的密实度；其余四种级配均只能用变k法表达，表明该四种级配设计理念是在连续级配的基础上，结合了填充理论，目的在于形成粗集料嵌挤、细集料填充的良好状态。

与k法比对时，AK-16和Novachip B型级配，k只能取固定值，GAC-16和SMA-16有k取值的区间。表明GAC-16、SMA-16相比于AK-16、Novachip，前两者级配的波动对其影响更小，后两者稳定性要求更高。

结合AK-16的路用性能表现及易出现水稳病害的特点，可以看出，AK-16虽在粗集料的嵌挤方面呈现了一定的优势，但是细集料填充不够。

针对AC-16密实却用于沥青面层容易出现高温稳定性不足的特点，GAC-16结合了AK和AC的优点，粗集料形成了有效嵌挤，而细集料也形成了有效填充，是一种进步。

对比GAC-16 与SMA-16，可以看出，SMA相比于GAC，粗集料形成嵌挤更强，细集料填充更密。从经济上考虑，可以认为GAC是一种经济型的SMA。

而相比于AK-16，NovachipB型在k值取值上虽具有某些相似的特征，但是Novachip应用的成功案例较多，主要是因为公称最大粒径和进一步的粗集料嵌挤作用，是一种值得深入研究的级配类型。

从以上的对比分析过程也可以看出，根据国内级配的发展历程及工程应用经验，用于沥青面层的级配正朝着粗集料嵌挤、细集料填充的方向发展，即常说的嵌挤密实型级配。具体对于16型级配而言，为了获得嵌挤密实型的级配，采用变k法设计或检验时，4.75mm以上k值应小于0.55，4.75mm以下应大于0.80为宜。

4 工程应用

在2018年粤赣高速公路路面专项养护工程中，对于出现存在抗滑性能不足和性能下降明显的隧道路面进行抛丸喷砂清理凿毛后，再加铺一层3cm厚薄层改性沥青混凝土罩面进行处治。

薄层罩面采用变k法理念进行设计，并通过马歇尔试验、高温车辙试验、浸水马歇尔试验及冻融劈裂等一系列试验来验证其路用性能。试验结果表明,所设计的沥青混合料满足施工技术要求,且薄层罩面通车运营已将近5年，具有良好的路用性能。可以看出，采用变k法设计的混合料性能优良，其设计方法可靠。

5 结论

(1)k法与AC-16可较好地对应，为连续密级配，设计理念为密实；变k法可体现AK-16、GAC-16、SMA-16及Novachip B型级配，为不同程度的嵌挤密实级配。在嵌挤的基础上，融合了填充理念，其嵌挤状态排序为：Novachip B型>SMA-16>AK-16>GAC-16。

(2)沥青面层级配正朝着粗集料嵌挤、细集料填充的方向发展，即嵌挤密实型级配。

(3)对于16型级配而言，为了获得嵌挤密实型级配，采用变k法设计或检验时，4.75mm以上的k值应小于0.55，4.75mm以下的k值应大于0.80为宜。