悬索桥锚跨张力控制方法研究*
胡志坚,黄健伟
武汉理工大学交通学院,湖北武汉 430063
地锚式悬索桥主缆架设过程中,锚跨索股张力控制应是悬索桥施工控制的重要内容[1-3]。为确保主缆索股在架设期间不发生滑移,同时使成桥主缆索力及散索鞍位置与设计值相符,在主缆架设完成后必须对锚跨张力和散索鞍偏角进行调整。传统的索力调整方法未能有效地考虑散索鞍偏角与锚跨张力之间的耦合关系,往往需要进行多次反复调整,逐渐逼近设计状态,具有一定的盲目性,且每轮索力调整都需要反复装卸千斤顶,操作繁琐,延误工期[4]。
近年来,众多学者对锚跨张力和散索鞍偏角的控制进行了一些研究。谭红梅等[5]指出温度变化对锚跨与边跨索力的影响不同,会使索股两侧产生较大的不平衡力导致索股滑移,但未分析不平衡力对散索鞍偏角的影响。唐茂林等[6]推导了索鞍移动刚度的计算公式,但未考虑转动刚度,不适用于摇轴式散索鞍。曾贤强[4]提出了一种根据实测散索鞍偏角与理论的差值,确定索力调整量的方法,但不能量化调整后温差和边跨垂度偏差对散索鞍偏角的影响以及调整量过大导致的索股滑移问题。沈锐利等[7]基于影响矩阵法建立了锚跨索弹性伸长量与散索鞍偏角的关系式,提出了锚跨张力及散索鞍偏角施工调整的计算方法,但该方法较为复杂。另外,由于索股架设过程中,边跨标高观测较为困难,施工误差引起的边跨垂度偏差要明显高于中跨,而锚跨较短时温差引起的散索鞍两侧不平衡力也相应增加。因此,需要进一步开展散索鞍偏角因素和锚索索力调整简化方法研究。
本文基于散索鞍转动刚度,分析了温度变化及边跨垂度偏差对散索鞍两侧不平衡力的影响,导出了散索鞍两侧不平衡力与散索鞍偏转角的关系式,提出了一种考虑散索鞍转动效应的索力调整方法。并结合具体工程实践,验证了该方法的有效性。
1 散索鞍转动刚度
根据悬链线理论,对于如图1所示的在自重作用下的柔性悬索段无应力长度为S0,索段截面积为A,弹性模量为E,沿索长方向自重集度为q,两支点跨度为X,高差为Y,左端竖向反力为V,右端竖向反力为V′。左右两端水平张力相等,设为H,则有[6,8]
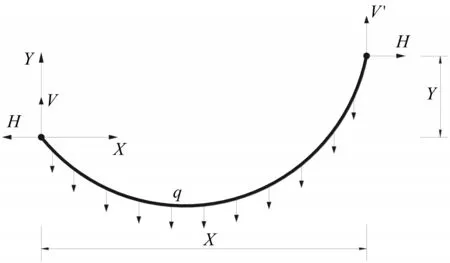
图1 自重作用下柔性悬索段受力图式Fig.1 Force diagram of flexible suspension section under the action of dead weight
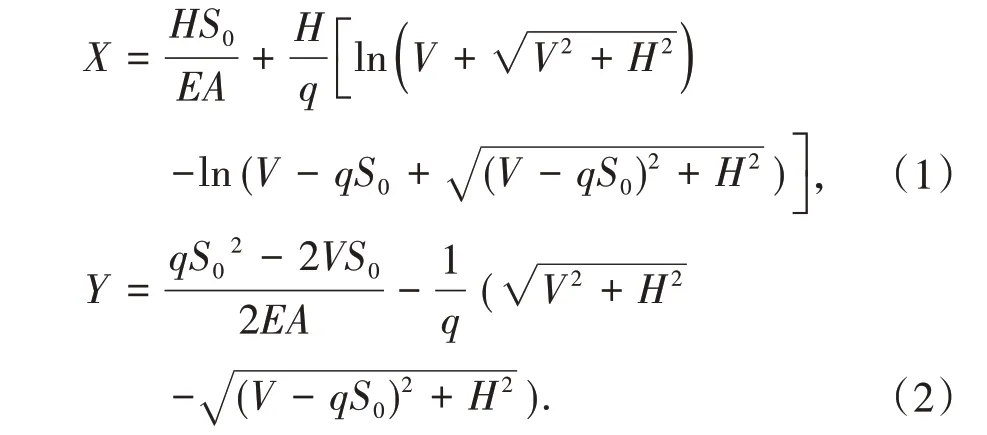
对式(1)、(2)求全微分得
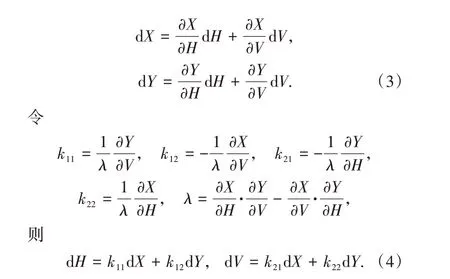
散索鞍受力如图2 所示,α为散索鞍倾角,锚跨主缆张力、竖向分力和水平分力分别为T1、V1、H1,边跨主缆张力、竖向分力和水平分力分别为T2、V2、H2.
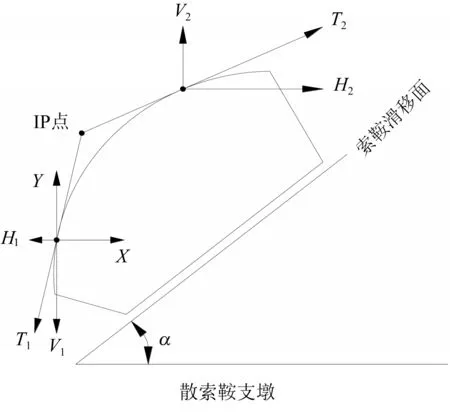
图2 散索鞍受力图式Fig.2 Force diagram of saddle
边跨、锚跨主缆内力在散索鞍滑动面上产生的不平衡分力为

假设散索鞍沿滑移面移动距离ds,由式(4)得主缆的内力变化为
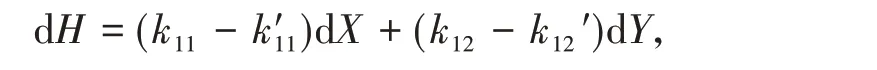

2 散索鞍偏角的影响因素
2.1 温度变化
2.1.1 对锚跨张力的影响由于锚跨索股一般较短,垂跨比很小,可近似地将索股看作固定于散索鞍和锚头之间的直杆,由温度变化引起的张力变化△Tmt为
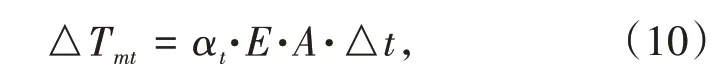
式中αt为索股的线膨胀系数;E为索股的弹性模量;A为索股截面积;△t为温度变化值。
2.1.2 对边跨张力的影响不同于锚跨,边跨的垂跨比较大,由温度变化引起索长改变从而引起索股垂度变化的影响不可忽略,因此边跨不能近似地看作两端固定的直杆[5,9]。根据悬索桥的抛物线计算理论,索长变化与垂度变化的关系式为
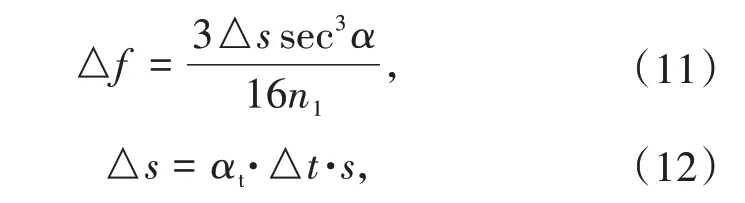
式中△f、△s分别为垂度变化量和索长变化量;α为边跨侧主缆的倾角,α= arctan(C/l),C、l分别为索两端点竖直方向和水平方向的距离;n1=f/l,f为边跨的跨中垂度,s为索长。
将(12)代入(11),得
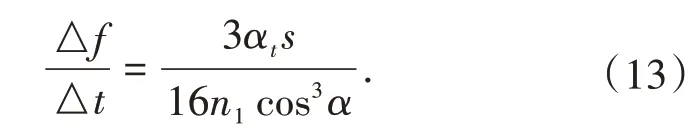
将索的自重近似看作沿跨径方向的均布竖向荷载q,则水平张力随垂度变化的关系式为
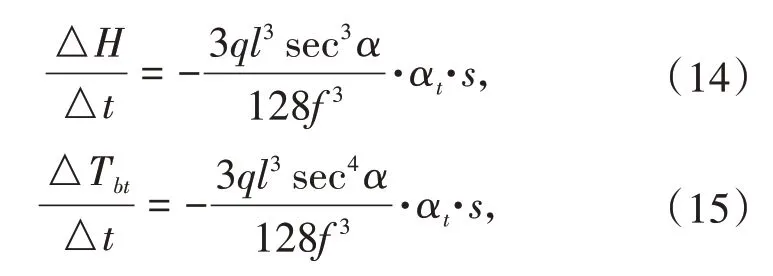
式中△H,△Tbt分别为温度变化造成边跨水平张力和索力的改变量,其余符号含义同上。
由于实际架索时的温度一般不等于基准温度,温度变化对边、锚跨索股索力影响不一样,导致散索鞍两侧出现不平衡力,从而使散索鞍产生偏转。
2.2 边跨垂度偏差
在实际主缆架设过程中,各类施工误差会导致实际边跨垂度与设计值有偏差,使得边跨侧主缆张力不等于设计张力,在散索鞍两侧产生不平衡力,使散索鞍产生偏转。
将主缆自重荷载近似看作沿跨径均布,则主缆张力为

当散索鞍解除临时约束后,由于温度变化和垂度偏差带来的不平衡力△T与散索鞍偏角θ之间的关系式为
式中K为散索鞍转动刚度;当架设温度高于基准温度时,△Tmt、△Tbt均为正;当实测边跨垂度高于设计垂度时,△Tbf为正;θ> 0 时,表示散索鞍相对于理论位置往边跨方向偏转。
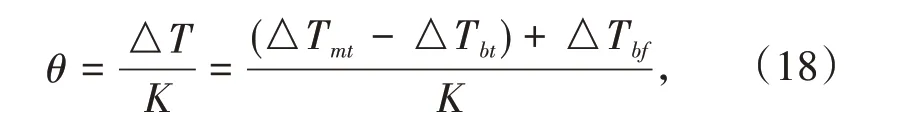
3 锚跨张力调整方法
主缆索股架设完成后,需要对锚跨索力进行精确调整,使索力达到理论设计值,散索鞍转动至设计位置,同时还要确保调整过程中不会出现索股滑移现象。
3.1 索力调整量计算
设主缆架设完成后,散索鞍相对于设计位置偏转角实测值为θ。若索力调整时的温度和边跨垂度能与设计值相等,则调整完成后散索鞍将偏转θ而回到设计位置;若温度与边跨垂度达不到设计值,散索鞍不会达到设计位置,因此需要对θ进行修正。
据式(18)可知,索力调整完成后散索鞍将偏转且
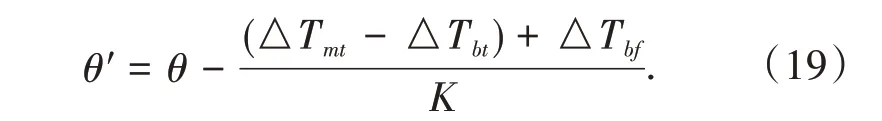
θ′> 0表示散索鞍向锚跨方向偏转。
在散索鞍转动过程中,由于锚跨索股在散索鞍上的切点坐标变化导致的索力变化很小,一般忽略不计,则可认为散索鞍的转动使得锚跨索股弹性伸缩。由于散索鞍转动导致的第i根索股的弹性伸缩量

式中rn为第n层索股在散索鞍转动时的转动半径。
设第i根索股理论目标索力为T0i,当前实测索力为Tsi,索股弹性伸缩单位长度的索力变化量Tdi为

式中li为第i根索股的无应力长度。则该索股的索力调整量为
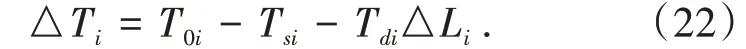
上式即为考虑散索鞍转动情况下的单根索股的索力调整公式,可以计算任意索股在当前状态下的索力调整量。对于锚梁式锚固系统,索力调整的方式主要是增减垫板,从而改变锚跨索股的弹性伸缩量。因此可以根据索力调整量求得所需增减垫板的厚度△di为
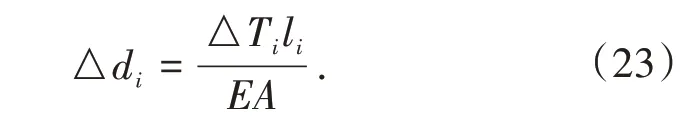
3.2 索力调整量优化
通过式(23),理论上可以一次性将索力调整至理论目标值,散索鞍回到设计位置。但是,对于单根索股,若索力调整量过大,可能会造成索股滑移,因此需要确定每一轮次调整的极限值。
当某次调整中索力调整量大于在鞍槽中的摩擦力时,索股会发生滑移,影响边跨线形,因此有必要对索股在鞍槽中的摩擦力进行研究。根据《公路悬索桥设计规范》,鞍槽内主缆抗滑移系数Ks应满足
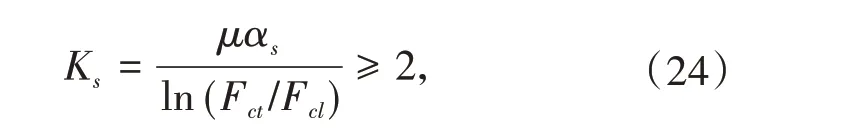
式中μ为索股与槽底或上下层索股间的摩擦系数,取0.15。对于μ,文献[10]里根据华盛顿桥的实测情况,认为μ取0.2 已足够安全;αs为主缆索股在鞍槽上的包角(弧度);Fct、Fcl分别为索股紧边与松边的拉力。μ和Ks的取值偏向保守,在实际施工过程中,安全系数可以适当减小,一般取Ks≥1即可[5]。取Ks=1,代入式(24)并对公式两边取对数得
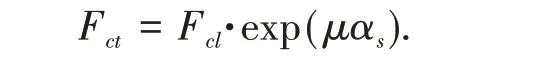
由此可知摩擦力
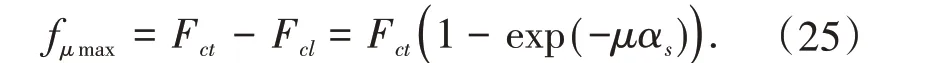
在索力调整过程中,要保证主缆索股不产生滑移,分以下两种情况考虑:
①当被调索股张力偏小时,需进行张拉,此时应保证张拉后的锚跨张力不大于边跨张力与散索鞍能提供的最大静摩擦力之和,即
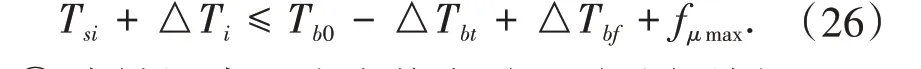
②当被调索股张力偏大时,需进行放松,此时应保证放松后的锚跨张力与散索鞍能提供的最大静摩擦力之和不小于边跨张力,即
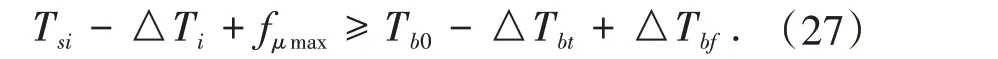
式中Tb0表示基准温度下边跨索股张拉力,△Tbt、△Tmt分别为由温度变化造成的边跨和锚跨索力变化量,△Tbf为由边跨垂度差异造成的索力变化量,其余符号含义同上。
通过式(26)、(27)即可确定每轮次索力调整时各根索股的最大调整量。若按式(22)计算的调整量大于最大调整量时,需要分轮次调整,直至达到设计值。由于索力张拉过程中主要靠千斤顶的油压表进行控制,存在施工误差,同时垫板和锚梁的加工尺寸存在偏差,因此在调整完成后需要再次对索力进行测试,校核索力误差是否在设计容许范围之内,如不满足,应再次进行调整直至索力误差满足精度要求。索力调整计算的流程图见图3。
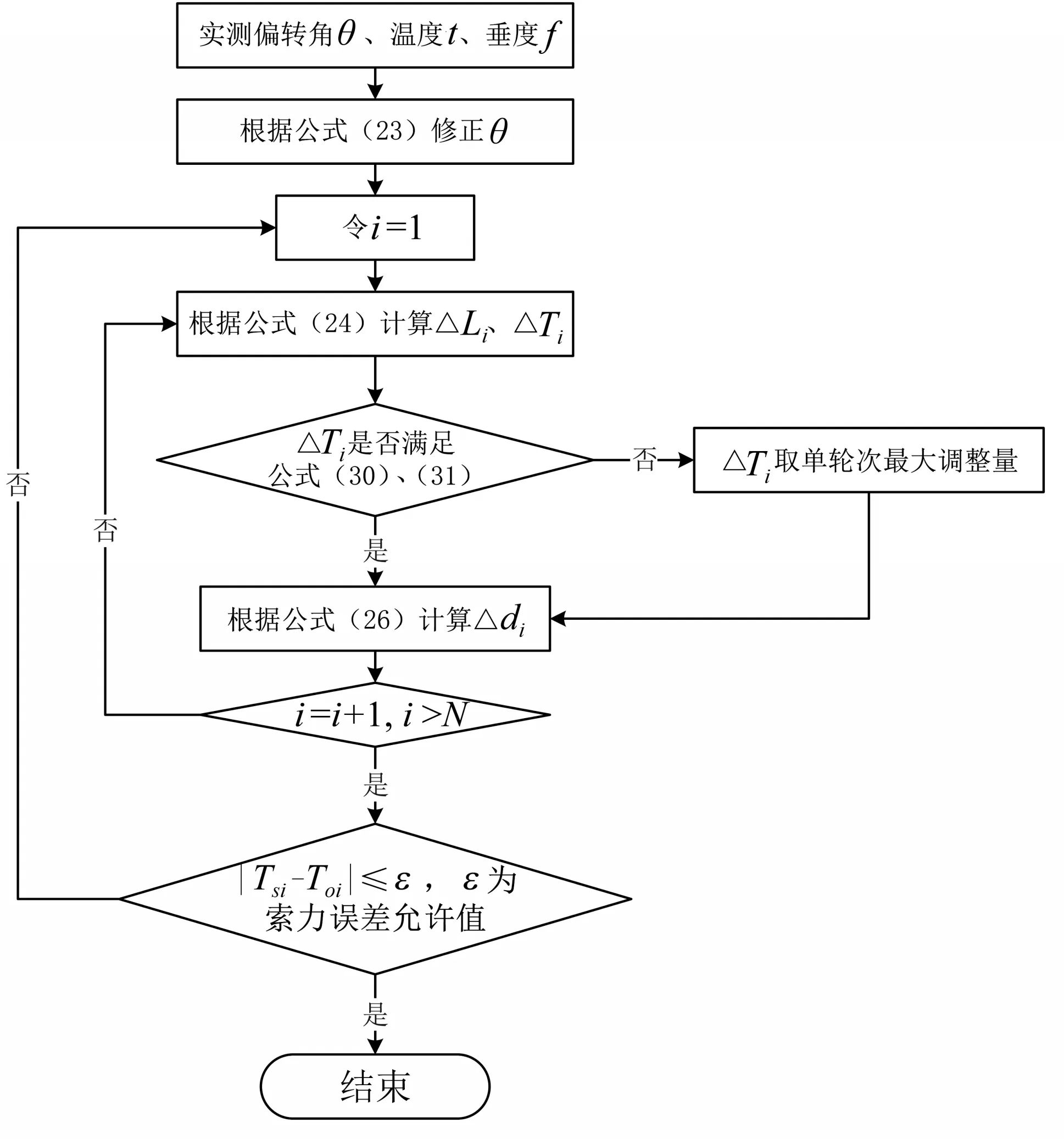
图3 索力调整计算流程图Fig.3 Calculation flow chart of cable force adjustment
4 工程实例分析
4.1 工程简介
某三塔两跨悬索桥,主缆跨度布置为(95+378+ 378+ 158)m,主跨矢跨比1/9,矢高42.0 m,桥型布置图如图4所示。主缆采用预制平行钢丝索股(PPWS)法形成,单根主缆由61 根索股组成,每根索股由127丝直径为5.2 mm、公称抗拉强度为1860 MPa 的锌铝合金镀层高强钢丝组成,全桥共两根主缆。单根索股面积A= 2 695.8 mm2,弹性模量E= 2.04 × 105MPa,线膨胀系数αt= 1.2 × 10-5。在主缆架设过程中,大桥两端散索鞍相对于设计位置均往边跨发生了偏转,最大偏转角为0.040°。如图5,散索鞍锚跨侧支撑与鞍体间隙达2.1 mm。
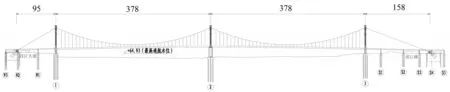
图4 桥型立面布置图(单位:m)Fig.4 Vertical layout of bridge(unit:m)
4.2 相关参数取值及计算
以北边跨为例,跨径l= 94.477 m,高差C=56.021 m,无应力长度S0= 168.011 m,沿跨径方向线荷载q= 14.91 kN/m,跨中垂度f= 2.679 m,边跨近散索鞍处主缆水平分力H= 6 209.623 KN,竖向分力V= 2 952.634 KN,散索鞍倾角°α= 39∘,IP点至散索鞍转动中心的距离lr= 3 m。
4.2.1 转动刚度根据式(9),代入相关参数,计算得到全部索股架设完成后的散索鞍转动刚度为7 405.42 MN/rad。
4.2.2 摩擦力索股与槽底或上下层索股间的摩擦系数μ= 0.2,包角αs= 0.698,索股紧边拉力Fct= 133.5 kN,根据式(25),计算索鞍在鞍槽中的最大静摩擦力fμmax= 17.5 kN。
4.2.3 温度的影响按照式(10),(15)计算温度变化对锚跨和边跨索股索力的影响分别为:△Tmt/△t= -6.47 kN/℃、 △Tbt/△t= -0.9 kN/℃。可以看出,当散索鞍固定时,温度变化对锚跨索力的影响远大于边跨。当温度变化为1℃时,散索鞍两侧单根索股不平衡力可达到5.57 kN。本算例中索力调整时实测温度为29 ℃,则单根索股带来的散索鞍两侧不平衡力将达到50.13 N,占初始索力的46%。
同时运用Midas Civil 及本文理论方法分别计算温度变化在-20℃,-10℃,10℃,20 ℃时锚跨及边跨单根索股的索力变化量,如图6所示。可以看出,有限元计算结果与理论计算结果吻合。
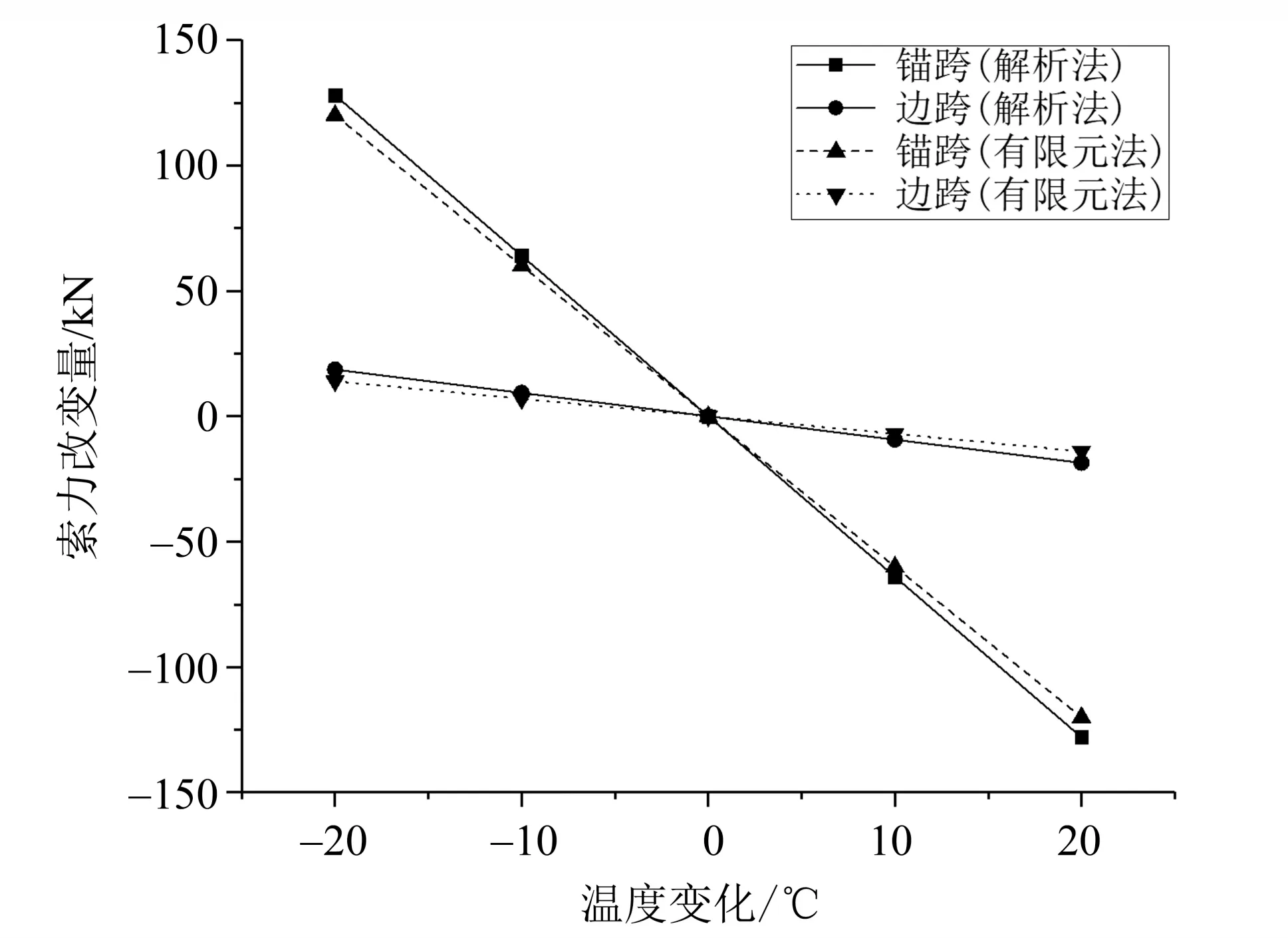
图6 锚跨及边跨索力与温度变化关系图Fig.6 Relationship between cable force and temperature of anchor span and side span
4.2.4 边跨垂度的影响根据式(17),代入相关参数,计算得边跨单根索股索力随垂度的变化量为-0.5 kN/cm。通过边跨垂度控制,本项目实测的边跨垂度偏差为6 cm,因此由于垂度差异造成的边跨索力变化量为3 kN。
4.3 索力调整
以北锚跨1#索股为例,根据式(20),由散索鞍转动导致弹性伸缩量△L1= 0.6 mm;该索股单轮次的最大索力调整量△T1max为15.5 kN。索股弹性伸缩单位长度的索力变化量Td1= 40.1 kN/mm。
1#索股实测索力与理论值的差值为-5.1 kN,根据式(22),则该索股的索力调整量△T1=-5.1- 40.1× 0.6 = -29.1 kN,大于单轮次最大索力调整量,需要分两次调整,第一次调整量取15.5 kN,所需增加的垫板厚度△di= 0.4 mm。
对其余索股进行了类似的调整,按式(22)计算的调整前索力调整量见图7。
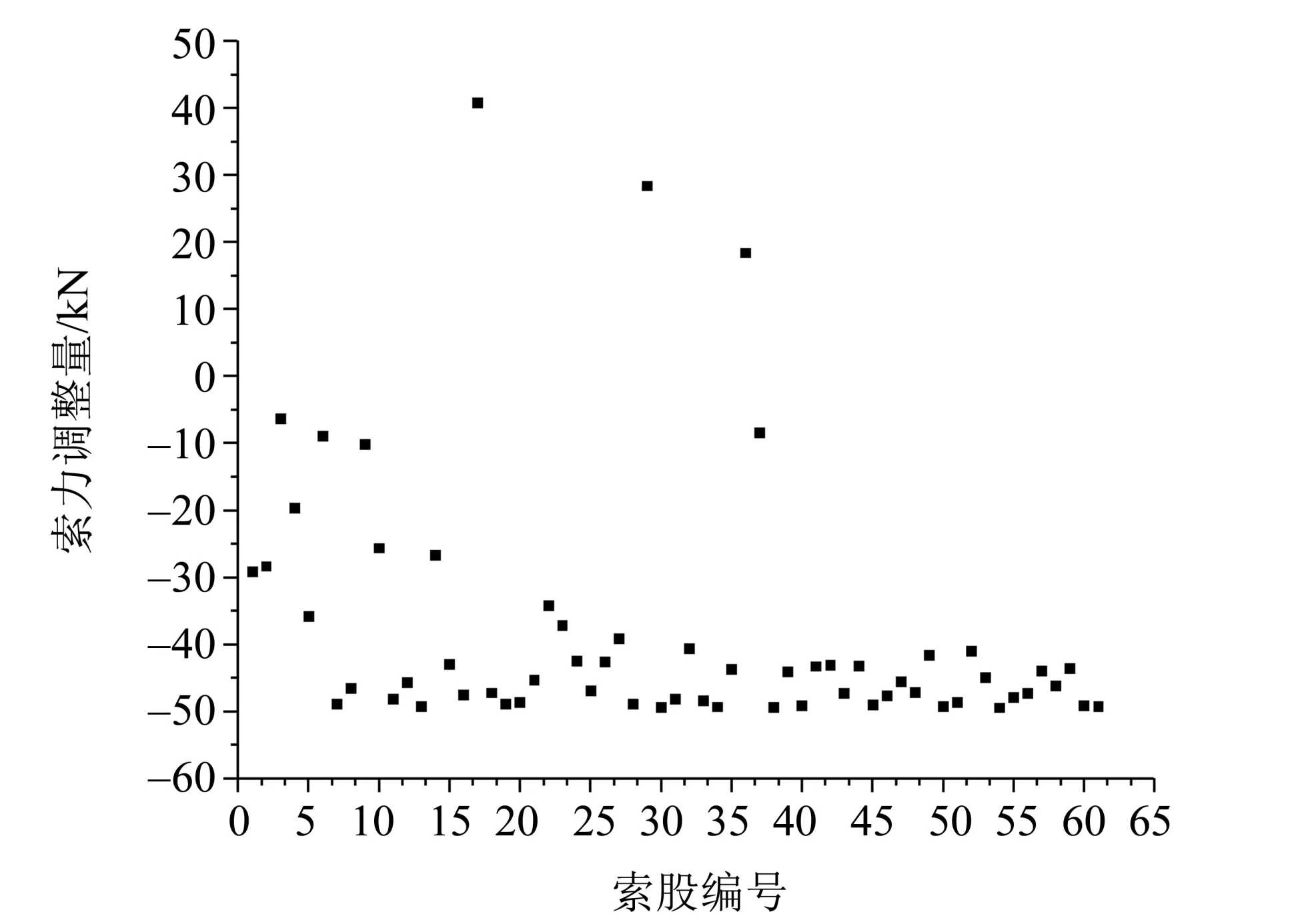
图7 索力调整量Fig.7 Cable force adjustment value
本项目共进行了三轮索力调整,各轮次索力调整结果如图8-10 所示,可以看出,经过三轮调整后,索力偏差在3 kN 以内,满足锚跨张力施工控制的精度要求。
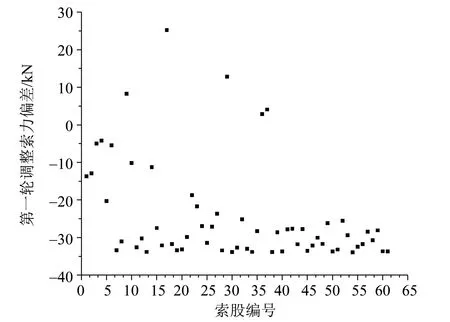
图8 第一轮调整索力与理论值偏差Fig.8 Deviation between cable force and theoretical value in the first round of adjustment
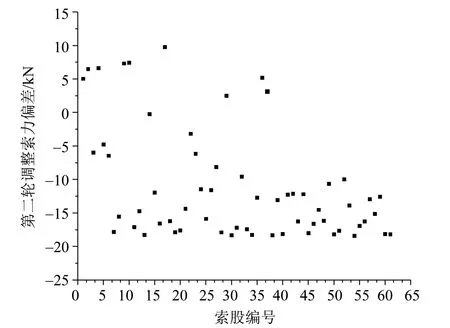
图9 第二轮调整索力与理论值偏差Fig.9 Deviation between cable force and theoretical value in the second round of adjustment
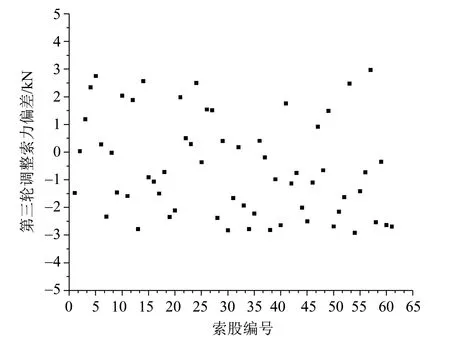
图10 第三轮调整索力与理论值偏差Fig.10 Deviation between cable force and theoretical value in the third round of adjustment
通过以上的调整可以发现,新的锚跨张力调整方法可以考虑散索鞍转角与锚跨索力之间的耦合关系,能显著减少调整次数,调索精度较高;同时,通过确定单次调整中的最大调整量,可以有效地避免索股发生滑移,保证边跨线形不发生改变;该法克服了传统调整方法的盲目性和危险性,能对锚跨张力进行有效的控制,具有操作简单、节省工期以及安全性较高等优点,可行性较好。
5 结 语
通过分析温度和边跨垂度偏差对散索鞍偏角的影响,结合某三塔悬索桥锚跨索股张力的调整实践,可以得到以下结论:
1)温度变化对锚跨的影响远大于边跨,使得散索鞍两侧出现不平衡力,是造成散索鞍偏转的主要原因;
2)本文基于散索鞍转动刚度,根据温度变化和边跨垂度偏差对散索鞍偏角的影响,推导出散索鞍偏角的计算公式,其正确性及计算精度已在工程实践中得到了印证;
3)本文提出的考虑散索鞍转动效应的锚跨张力简化调整方法,具有显著减少调整次数、能有效避免索股发生滑移、节省工期以及调索精度较高的优点,已成功应用于工程实践。
——垂度法

