基于经验分布下GARCH模型对VaR的金融测度*

李翠霞，陈媛媛

1. 徐州工程学院数学与统计学院，江苏徐州 221111

2. 兰州大学数学与统计学院，甘肃兰州 730000

随着金融体系的不断完善，全球金融市场进入了高速发展的阶段，随之而来的金融风险也受到了人们的广泛关注。众所周知，金融风险不仅严重影响企业的生存与发展，同样对金融机构及整个国家的经济运行都会产生巨大的冲击。20世纪90年代以来一些大的金融机构所经历的金融危机，大多是不能有效地管理其面临的市场风险，如巴林银行、德国金属期货公司、日本大和银行等都在金融市场上遭受了几十亿美元的损失。在这一连串举世瞩目的衍生品灾难发生以后，人们呼吁重新评估整个风险管理体系，包括用于衡量风险的工具，在这一前提下，1994年摩根大通［1］提出的VaR（Value at Risk，在险价值）方法在这个时代背景下成为一种强有力的风险管理方法，同年10 月，他将建立的RiskMetrics模型的资料和相关方法论公诸于世，市场上所有参与者都可以通过网络得到相关资料。至此，在金融风险管理领域，世界上一些主要的银行和金融机构越来越重视对VaR 的使用，这是一种容易理解和掌握的计算和控制市场风险的方法。VaR 最重要的特征还在于它的透明性，仅仅一个数值就可使任何人都清楚风险多大。Artzner等［2］证明VaR 在理论上不满足次可加性，但它在风险度量领域所起到的重要性是不可忽视的。尽管存在这一缺陷，但行业和银行部门的监管机构都更喜欢使用VaR，而不是满足次可加性的风险度量指标——预期缺口（Expect Shortfall，简称ES）。主要是因为VaR具有很多实际优势，比如较小的数据需求，易于回溯测试，在某些情况下易于计算等。

1 模型设定

金融收益率序列有两个非常重要的特征：异方差性和重尾现象。为了描述金融数据的这种特征，En‐gle［3］提出了ARCH 模型，在此基础上，Bollerslev［4］建立了GARCH（广义ARCH）模型。随后，Boller‐slev等［5］、Taylor［6］将这些模型应用于风险（股票价格、金融指数、外汇汇率等）计量中存在的长期依赖问题。Chang 等［7］在前人的研究基础上，提出分别使用GARCH、EGARCH、GJRGARCH 等波动率模型对VaR 进行建模，并将条件分布分别设为高斯分布和t分布。Francq［8］在标准GARCH 对VaR 建模的过程中，将条件波动模型的参数形式设为εt=σt(θ0)ηt，认为VaR的计算结果取决于ηt创新分布的过程，而不取决于波动率参数θ0。因此本文在Francq［8］的理论基础下，利用标准GARCH（1，1）模型拟合波动率，同时结合残差经验分布函数这种分布形式对VaR进行建模分析。

标准的GARCH（1，1）模型为

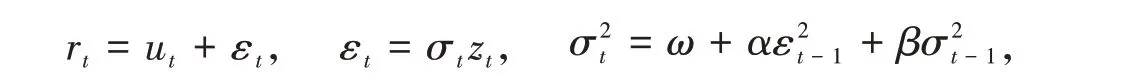
其中ut为收益率序列t时刻的均值，εt是收益率序列t时刻的残差，zt是均值为0，方差为1 的独立同分布（iid，independently identically distribution）的随机变量序列（即zt～iid（0，1））。在这里，我们不指定zt的具体分布，因此形成了更加有利的半参数模型。因事先未指定zt的具体分布，因此避免了由于模型与实际情况不符造成的失效。同时，我们的模型因为在参数模型的框架下，因而又避免了非参数模型面临的维数灾难等问题。

1.1 VaR的概念

VaR指在给定的概率水平下，金融产品在某一特定时间段内的最大可能损失。即

P(△P> VaR)= 1-τ，

其中△P为金融产品在持有期△t内的损失，VaR 是在置信水平τ下可能产生的最大损失值。例如：在90%的置信水平下，某公司一天的VaR值为500万美元，指该公司以90%的把握保证，在一天内由于市场价格变动所带来的损失不会超过500万美元。

在本文中用Q(τ)= VaR1-τ表示在置信水平τ下的VaR值（最大损失）。

1.2 模型设定

假设VaR =G(Θ，zi)，G(∙)的形式通常有GARCH、EGARCH、GJRGARCH 等设定形式。这里主要讨论尾部分布形式，为了尽可能减少参数估计量，我们使用标准GARCH（1，1）模型为基础建立模型，即

这里用Q(τ)= VaR1-τ=G(Θ，Qz(τ))表示，其中Θ =(μ，ω，α，β)为标准GARCH（1，1）模型中的参数，Qz(τ)为zi的τ阶分位数。以下分3个步骤来进行计算。

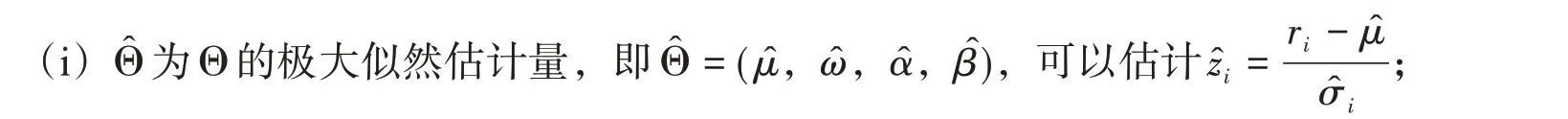
1.3 模型评价方法

1.3.1 失败频率检验对度量VaR 的模型准确性检验指的是模型的度量结果对实际损失的覆盖程度。例如：给定99%置信水平下的VaR 值，若实际损失超过预期VaR 值的概率大于1%，说明模型预测失效。本文采用Kupiec［10］提出的失败频率检验法。其基本思想是观察实际损益超过VaR 值的概率。把实际损益超过VaR 值记为预测失败。假定VaR 的置信水平为τ，实际观测天数为T，预测失败天数为N，则失败频率为p=N/T，失败的期望概率为p*= 1-τ。此时，对模型准确性的检验等同于检验失败概率p是否等于给定概率p*，即检验的零假设是H0：p=p*。

Kupiec提出了对H0最合适的检验是似然比率检验

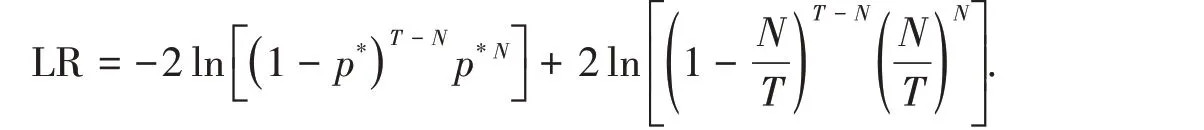
在假设H0下，统计量LR服从自由度为1的χ2分布。失败频率检验法应用广泛，但是当基于每日回报的基础之上，数据量较少时很难评价模型低估潜在损失的情况。因此，这种模型评价方法通常基于长期数据观测的前提下。

1.3.2 相对误差为了体现模型的准确性，本文在失败频率这个指标基础上增加了一个新的评价指标——相对误差（Relative Error，RE），可以写为

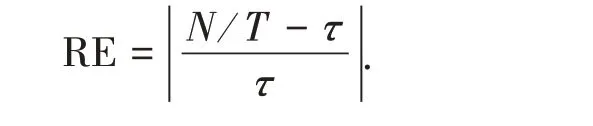
相对误差越小，说明对VaR的预测效果越准确。

2 基本数据分析

选取的数据是道琼斯指数（DJIA）2009 年1 月2 日至2019 年12 月31 日的数据（见图1），样本量为2 768个数据，我们将前2 476个数据作为训练集，用于模型的建立，后292个数据作为测试集，用来观察模型的预测准确程度。本文采用对数收益率，即rt= lnpt- lnpt-1，pt为第t日收盘价。相对于一般收益率，采用对数收益率主要有以下几点原因：①对数函数使得收益率的取值扩展到整个实数域范围，对于金融产品的建模更为合适。②通过对收益率取对数，将原本计算中的乘法运算变为加法运算，简化了计算过程。③对时间序列的数据进行建模时，推导时间序列之和的计算更加方便，使得模型建立更简单。

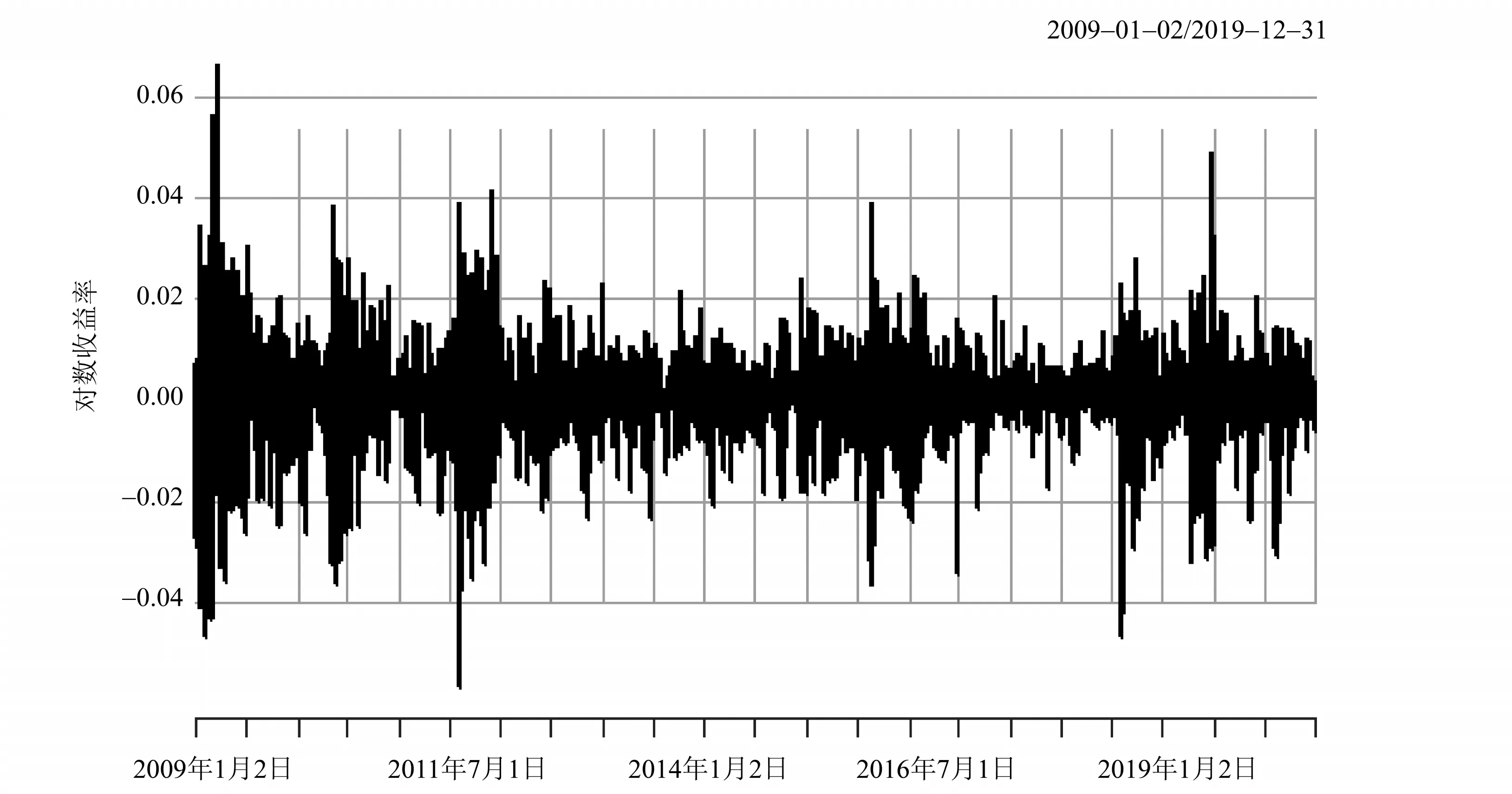
图1 道琼斯指数日收益率Fig.1 DJIA index daily return

2.1 数据基本特征

从图1可以看出我们研究的数据是比较平稳的，并且也能够看出金融时间序列存在的波动丛集性特征（大的波动后面常伴随大的波动，小波动的后面跟随小的波动）。从数据的基本特征来（见表1）看，道琼斯指数（DJIA）的偏度分别为-0.315 80（<0），峰度分别为4.643 77（>3），同时其JB统计量为2 254.568，并结合QQ图（见图2）可以看出，研究数据不服从正态分布，并具有尖峰厚尾的特征。

表1 数据基本特征统计Table 1 Data basic characteristics statistics

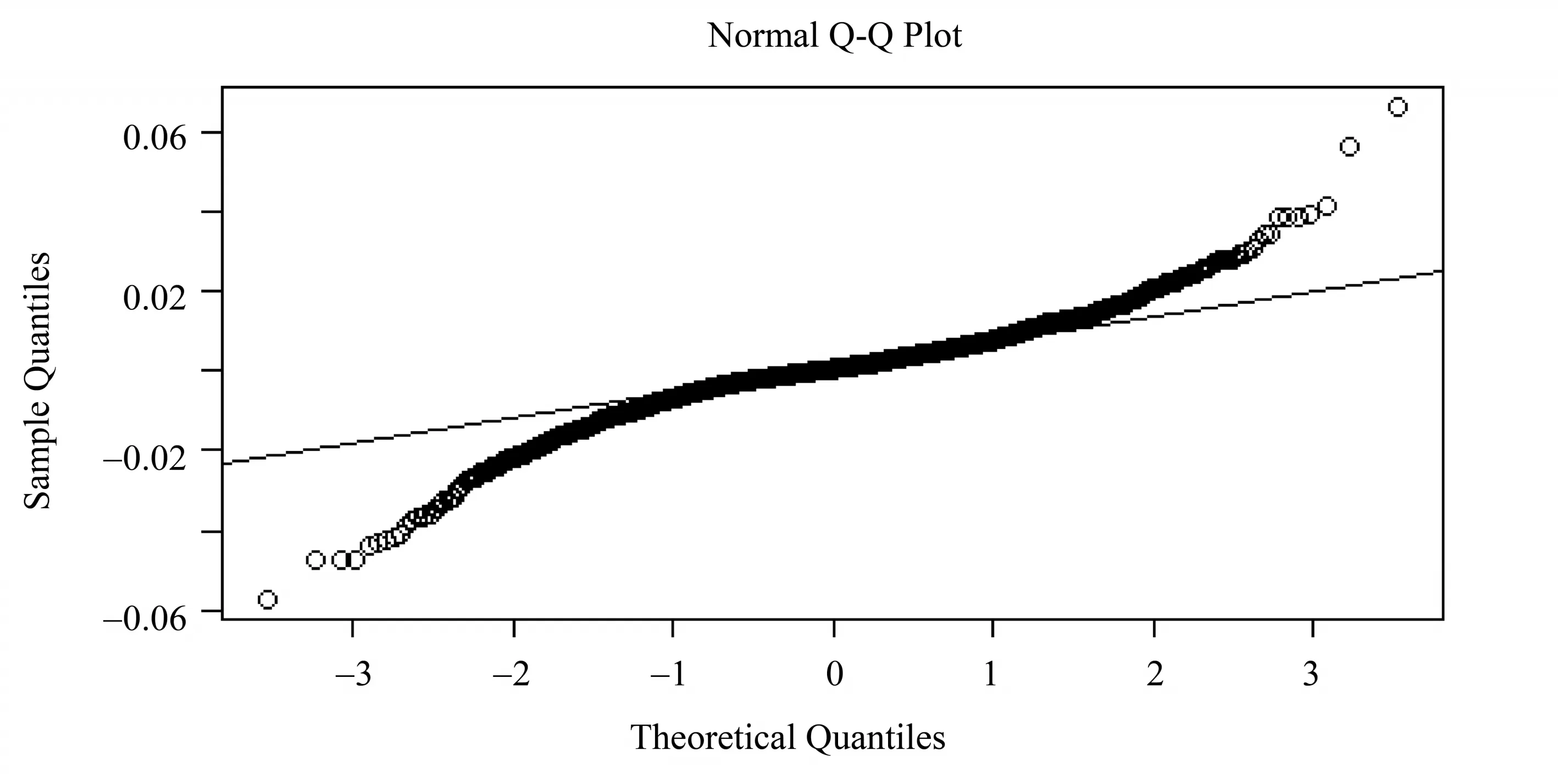
图2 道琼斯指数QQ图Fig.2 DJIA QQ plot

2.2 平稳性检验

对时间序列数据进行分析建模前，首先需要对序列是否平稳进行检验。在此，我们采取了ADF（Augmented Dickey-Fuller test）［11］检验和PP（Phillips-Perron Unit Root Test）［12］单位根检验。

2.2.1 ADF检验ADF检验通过在回归方程右边加入因变量yt的滞后差分来控制高阶序列相关。

（I）无常数项、无趋势项的p阶自回归过程：yt=γ1yt-1+ …+γpyt-p+ξt.

（II）有常数项、无趋势项的p阶自回归过程：yt=ρ+γ1yt-1+ …+γpyt-p+ξt.

（III）有常数项、有趋势项的p阶自回归过程：yt=ρ+δt+γ1yt-1+ …+γpyt-p+ξt.

模型（III）中的t是时间变量，代表序列随时间变化的某种趋势。虚拟假设均为H0：γ= 0，即存在单位根，该序列不平稳。模型（III）与模型（I）、（II）的差别为是否含有常数项和趋势项，检验顺序为（III）→（II）→（I），何时拒绝零假设，何时停止检验，即该序列为平稳序列。经检验发现，在第一次检验（III）时即拒绝原假设，说明我们研究的序列是平稳的。

2.2.2 PP检验PP 检验优化的是DF 统计量，通过非参数方法来修正DF 统计量，使其具有滞后期估计功能。

道琼斯指数经过ADF 和PP 单位根检验结果分别为-13.943 和-53.086，它们的p值都远远小于0.01，在99%的显著性水平下拒绝了原假设，说明我们研究的收益率序列是平稳的。

2.3 异方差检验

Engle 在1982 年提出检验残差序列中是否存在ARCH 效应的拉格朗日乘数检验（Lagrange multiplier test），即ARCH-LM 检验。其零假设是序列不存在ARCH 效应，此时检验统计量渐近服从χ2分布。检验结果如表2所示。

表2 ARCH-LM检验Table 2 ARCH-LM test

检验结果p值可以看出，我们在滞后阶数为5阶、10阶、15阶均拒绝了原假设，即原序列存在显著的ARCH 效应。从以上的数据分析可以看出：收益率序列是平稳的，不服从正态分布且具有尖峰厚尾的特征，其次数据存在显著的ARCH效应，因此在这里使用GARCH模型是合适的。

3 模型预测与结果分析

GARCH（1，1）模型选取以下参数值：μ=7.45× 10-4，ω= 2.67 × 10-6，α= 0.149，β= 0.824，对数似然值为8 410.83。

3.1 模型预测

以下是我们分别使用指定条件分布为正态分布的GARCH（1，1）模型，以及经过我们提出的新方法修正后在样本外的测试结果（见表3）。

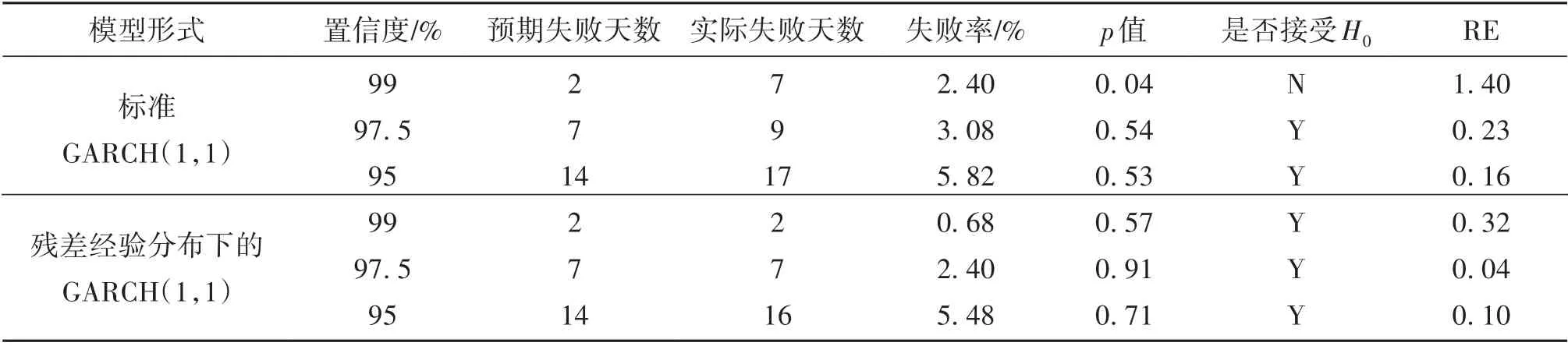
表3 道琼斯指数（DJIA）预测结果1）Table 3 Predicted results of DJIA

3.2 结果分析

通过Kupiec 失败频率检验结果看到，使用标准GARCH（1，1）建立模型，其预测效果表现不佳，尤其是在99%的置信水平下，利用标准的GARCH（1，1）模型预测结果，其实际失败天数是预期失败天数的数倍。可以看到传统的参数模型一旦指定条件分布是错误的，模型的表现效果就会很差。在我们利用新方法对残差进行修正后，实际失败率得到了很大的改善，不仅在各置信水平下通过了Kupiec失败频率检验，而且与预期失败天数十分接近。其次，我们采用的方法得到的相对误差也小于标准GARCH（1，1）模型下的误差，因此，我们的模型不仅修正了标准的GARCH（1，1）模型，并且在较高置信水平下对VaR 的度量更为准确。