马边滑坡运动特征及冲击强度的数值研究

陈 兴，赵 洲，魏江波，许 冲

马边滑坡运动特征及冲击强度的数值研究

陈 兴1，赵 洲1，魏江波1，许 冲2

(1. 西安科技大学 地质与环境学院，陕西 西安 710054；2. 应急管理部国家自然灾害防治研究院，北京，100085)

滑坡运动堆积特征及其冲击强度研究对滑坡风险定量评估具有重要意义。通过对四川乐山市马边滑坡基本特征调查，利用支持向量机模型(SVM)和颗粒流方法(PFC)，对滑坡岩土体细观强度参数进行反演和标定，结合UAV数据生成滑坡区高精度DEM，在此基础上，重构马边滑坡三维颗粒流数值模型，模拟并研究滑坡的运动堆积和冲击过程。结果表明：马边滑坡运动时长32 s，主滑时间16 s，运动开始5 s后速度达到峰值，为10.2 m/s；滑坡中后部岩土体运动迹线为直线型，中前部运动迹线成扩散状态，最终呈扇形堆积；滑坡在坡脚处的冲击力可达1.5×109N，并随着坡脚距的增大，冲击力呈现出指数衰减特征。研究结果与滑坡运动过程实际视频解译结果及堆积现状基本一致，相关研究方法为滑坡定量风险评估提供借鉴。

马边滑坡；支持向量机模型；颗粒流方法；滑坡运动特征；冲击强度

滑坡风险定量预测研究对滑坡灾害防灾减灾具有重要的理论和实际意义。随着计算机技术的快速发展，数值方法已成为模拟和分析滑坡致灾过程的重要研究途径，因其具有成本低、参数设置灵活、不受尺寸约束、兼容性强、重复计算等优点，近年来得到了广泛的应用[1]。

目前，研究人员基于不同理论与本构模型开发了可用于模拟滑坡变形、失稳破坏、运动、堆积等过程的数值模拟软件，如FLAC、MatDEM、UDEC、DDA、PFC、MassMov2D、Massflow、DAN等。其中，颗粒流(Particle Flow Code，PFC)程序能够模拟介质开裂、分离等不连续现象，非常适合滑坡动力学特征的模拟分析[2-3]，广泛应用于滑坡变形破坏特征分析、运动过程模拟和堆积特征研究等方面。Tang Chaolung等[4]、陈达等[5]基于PFC2D软件对滑坡体在不同工况下的破坏特征进行了模拟，对滑坡关键部位颗粒的位移、速度进行监测，对其运动特征进行了分析；Lo Chiaming等[6]和周礼等[7]运用PFC3D对滑坡的运动特征和堆积范围进行深入研究；Zou Zongxing等[8]和胡晓波等[1]分别基于PFC2D、PFC3D在研究滑坡运动基本参数的基础上，讨论了滑坡运动过程中能量的转化关系。相比滑坡运动堆积过程的模拟，对滑坡冲击致灾能力或冲击强度的数值研究对滑坡风险定量预测具有更加重要的实际意义。当前对滑坡冲击强度研究仅限于理想边坡或简化模型试验的数值模拟， Li Bin 等[9]基于PFC2D对理想化滑坡撞击挡土墙进行了一系列的数值试验，得出了坡体几何形状、滑体移动距离、墙体位置和滑面摩擦力对墙体冲击力的影响；Gao Ge等[10]和Bi Yuzhang等[11]基于PFC3D方法，结合模型试验研究了斜坡土体对挡墙的冲击强度。

随着无人机(UAV)技术的日趋成熟，大范围高精度数字高程模型(Digital Elevation Model，DEM)的构建及其在滑坡三维数值模型研究中应用越来越广泛，而基于高精度DEM的滑坡冲击强度模拟和应用研究较少。同时，应用PFC方法进行滑坡过程模拟研究的最大难点，在于设置符合滑坡岩土体宏观力学特征的细观强度参数，传统参数标定方法中往往需要通过大量模拟和试算加以确定，计算过程相当繁琐。为此，笔者将统计学习 VC 维(Vapnik- Chervonenkisdimension)和结构风险最小化理论的监督学习分类模型—支持向量机模型(Support Vector Machine，SVM)引入滑坡数值模型相关参数的标定当中。该算法采用核映射思想，在解决小样本、非线性、高维数的问题时表现出很好的优势[12]。由于SVM算法的优越性，其在工程地质领域受到广泛应用，包括滑坡敏感性评价[13]、边坡稳定性分析[14]、岩土体变形预测[15]及岩土参数反演[16]等诸多方面，在岩土体参数的快速学习和智能标定等方面具有显著的优势。

综上，为对滑坡动力学过程进行分析，并对冲击后造成的致灾强度进行定量化研究，笔者以四川省乐山马边滑坡为研究对象，在野外调查基础上，采用SVM和PFC相耦合的滑坡岩土体细观参数标定新方法，根据UAV所采集的高精度DEM数据，构建颗粒流滑坡三维数值模型，进而反演分析马边滑坡运动堆积特征与冲击强度大小，以期为滑坡定量评价提供新的思路。

1 马边滑坡概况

马边滑坡位于四川省乐山市马边彝族自治县三河口镇星星村(图1a)。滑坡发生于2018年5月5日12︰30，造成坡脚100 m公路掩埋，马边河堵塞。滑坡区在一年中呈现冬干春旱夏洪秋涝的降雨特征，属亚热带季风气候区。出露地层岩性主要为三叠系中统雷口坡组(T2)页岩、板岩，夹石膏，以及二叠系中统(P2)砂岩与粉砂岩[17]。根据现场调查，马边滑坡平面呈“梨”形，相邻于右侧古滑坡。滑坡滑前后缘高程约1 350 m，坡脚高程约1 195 m，前后缘高差约155 m，主滑方向258°，滑坡所处区域河谷深切，地形高差大，坡度约60º (图1b)。

图1 四川省乐山马边滑坡分布

如图2所示，滑坡发生后，其后缘及两侧分别因受拉张和剪切作用形成高低不一的陡坎，出露的基岩面上风化裂隙较为发育，造成前缘坡脚处河流堵塞，形成堰塞湖。滑坡堆积体产状为258°∠30°，堆积区最大宽度约220 m。

图2 马边滑坡灾后航拍图

2 马边滑坡三维模型构建

2.1 岩土体细观参数确定

本文引入支持向量机与颗粒流方法相耦合的机器学习法(SVM-PFC)，进行马边滑坡岩土体宏细观参数的标定。该方法是将大量基于PFC的单轴压缩试验结果数据通过支持向量机模型进行学习，建立宏细观参数之间的非线性映射关系模型，从而反演计算岩土体细观强度参数，其参数标定流程如图3所示。

根据上述SVM模型宏细观参数标定方法与岩石实际宏观强度参数可得对应滑坡体细观强度参数，见表1。

在PFC3D中使用表1参数进行虚拟单轴压缩试验，其试算结果与室内土工试验所获得的岩土体宏观力学参数基本吻合(图4)，从而证明SVM-PFC耦合方法进行岩土体细观参数标定具有较高的可靠性，进而可使用表1中相关参数构建马边滑坡的三维颗粒流模型。

图3 SVM-PFC耦合方法标定岩土体细观强度参数流程

2.2 马边滑坡模型构建

使用UAV(DJ Pro4)对马边滑坡进行航测，基于无人机影像，生成分辨率为0.15 m的DEM数据，并以此为基础，利用PFC3D颗粒流程序构建三维滑坡模型(图5)。同时，在滑坡前、中、后设置监测点，以便于研究滑坡运动特征(图6)。

滑坡在运动过程中，滑面参数对滑坡体运动状态影响较大，通过试验和分析[8,18]，滑面摩擦系数设置为滑面静摩擦系数(滑面倾角的正切值)的1/3倍，即wall=(tan45º)/3=0.33，同时，考虑到复杂的地形和植被特征，以及移动过程中滑坡对地表的刮擦和气垫效应，结合已有经验，设置坡面摩擦系数为0.35[4,19]。

表1 滑坡岩土体颗粒细观参数

E为压缩弹性模量；UCS为无侧限单轴抗压强度；n为泊松比

图5 马边滑坡三维数值模型

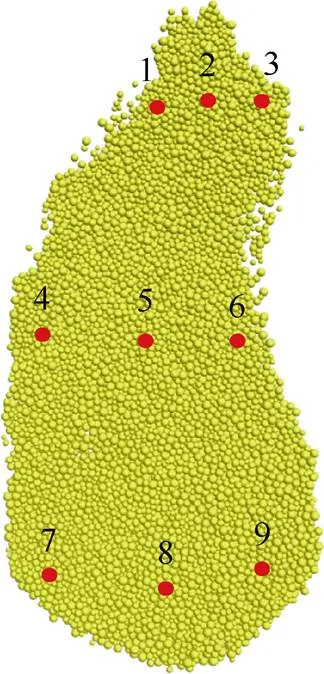
图6 监测点位置及编号

3 滑动过程模拟及结果分析

3.1 滑动过程模拟

从图7可知，通过建立的马边滑坡三维模型反演其滑动全过程，滑坡从失稳滑移到停止运动的整个运动总持续32 s，主滑时间 16 s。滑坡运动前期，前缘锁固段未出现明显位移(图7a)，之后在滑体自重作用下发生破坏，前缘剪出口土体产生明显位移(图7b)，从而使滑坡失稳并整体下滑。滑动开始5 s 左右滑坡体整体运动速度达到最大值，局部速度至少达到12 m/s(图7b)。随着滑体碰撞、崩解及摩擦对能量的耗散，滑坡运移速度逐渐减缓(图7c—图7e)，在滑动32 s 后大部分滑体停止运动并堆积于斜坡坡脚，此时滑坡处于相对静止阶段，且部分土体仍存在较小的运动速度(图7f；图8a)。

该滑坡反演结果与滑坡实际滑动过程视频解译结果基本吻合[17]。

在滑坡运动模拟过程中，对其后缘、中部和前缘各位置处选取的特征颗粒进行实时监测速度(图8)。由图8可知，滑坡各部运动速度特征均表现为随时间的增大先快速增大，后缓慢减小的特征。滑坡后缘平均速度峰值约8.5 m/s，中部滑体约9.8 m/s，前缘约 10.8 m/s，滑坡达到各部位速度峰值在4～8 s，滑坡体前缘速度峰值高于后缘速度峰值，且滑坡体前缘速度达到峰值与相对停止运动时间均早于后缘，表现为后缘运动的滞后性。同时，在滑坡体前缘相对静止阶段，后缘存在少部分岩土体仍在缓慢向下滑动。

通过自编FISH函数进行滑坡体整体平均运动速度与平均位移的实时监测。滑坡平均速度表现为先快速增大，后逐渐减小的特征，5.3 s时达峰值，约10.2 m/s，最远滑移距离约120 m(图9)。

文献[20]中的采用Scheidegor法进行理论计算滑坡整体峰值速度约为 11.4 m/s，与模拟结果10.2 m/s较为相近，由于理论计算并未充分考虑滑坡运动期间岩石块体间的摩擦、碰撞及冲击耗能，导致理论计算结果稍高于模拟结果。

3.2 堆积特征分析

根据滑坡滑动过程的模拟分析，滑坡滑前最大宽度约100 m，滑坡区最大宽度约220 m，马边滑坡滑源区与堆积区有一定的重叠，滑坡堆积体掩埋道路，堵塞河道，这一结果与滑坡发生后的调查结论完全一致(图10，图2)。

为更直观地分析滑坡岩土体的运动堆积特征，将滑体不同部位的颗粒进行分组显示，从染色分组的颗粒在滑前与滑后的位置对比(图10)可得，滑体大部分岩土体颗粒的空间排列次序在滑坡运动前后未发生明显变化，仅滑体尾部岩土体颗粒在滑坡运动后发生了一定程度的混合。

图7 马边滑坡运动过程

图8 马边滑坡不同位置速度

图9 马边滑坡平均速度与位移

通过对滑体不同部位颗粒运动轨迹的监测(图11)，滑体尾部颗粒运动轨迹呈汇聚状(图11a)；滑体中后部颗粒运动迹线基本为直线型，堆积与滑前宽度相近(图11b)；由于滑坡前缘地形开阔，中前部颗粒向前运动的同时向两侧扩散，呈扇形展布特征(图11c，图11d)。堆积体后缘部分位于滑坡区，与滑坡区产生一定的重叠，与滑坡实际堆积特征相符。这些特征均表明，利用离散元方法对马边滑坡堆积特征的模拟具有较高适用性。

图10 马边滑坡滑动后堆积特征

图11 颗粒运动迹线跟踪图

3.3 冲击强度研究

滑坡失稳后的运动冲击，一般都会对其运动方向上分布的建筑物、基础设施等造成不同程度的损毁。因此，滑坡冲击致灾能力或致灾强度的预测研究具有重要的意义。

目前研究人员多选择滑坡速度、动能、冲击力这3个指标来表征滑坡的致灾能力或冲击致灾强度大小[21-22]。本文选择滑坡在运动过程中作用于单位面积的冲击力指标来表征马边滑坡的冲击强度大小。通过在主滑方向上距离斜坡坡脚不同位置(简称为坡脚距，用i表示)处构建竖直刚性墙，并监测单位面积墙体所受滑坡冲击力与时间、坡脚距之间的变化特征，以此来分析滑坡对不同坡脚距位置处承灾体的冲击作用，从而间接评价滑坡的致灾强度大小。由于距坡脚56.5 m外是河谷且无建筑物，因而将刚性墙设置在56.5 m内。在该范围内设置8个滑坡冲击力测试刚性墙(图12)，分别模拟和监测刚性墙所受水平冲击力大小。

根据模拟测试结果，当挡墙坡脚距不同时，滑坡冲击力随坡脚距的增大明显减小(图13)。在初始滑动阶段，由于滑坡前缘颗粒快速碰撞挡墙，冲击力曲线出现一个极大值点，颗粒在碰撞后立即减速，甚至出现回弹现象，因此，冲击力在极大值后出现短暂减小。随着滑坡堆积体体积的不断增大和持续冲击，冲击力随时间的增加而增大，当滑坡减速堆积并最终停止运动后，冲击力逐渐趋于稳定，并表现为滑坡堆积体对墙体的静止土压力。

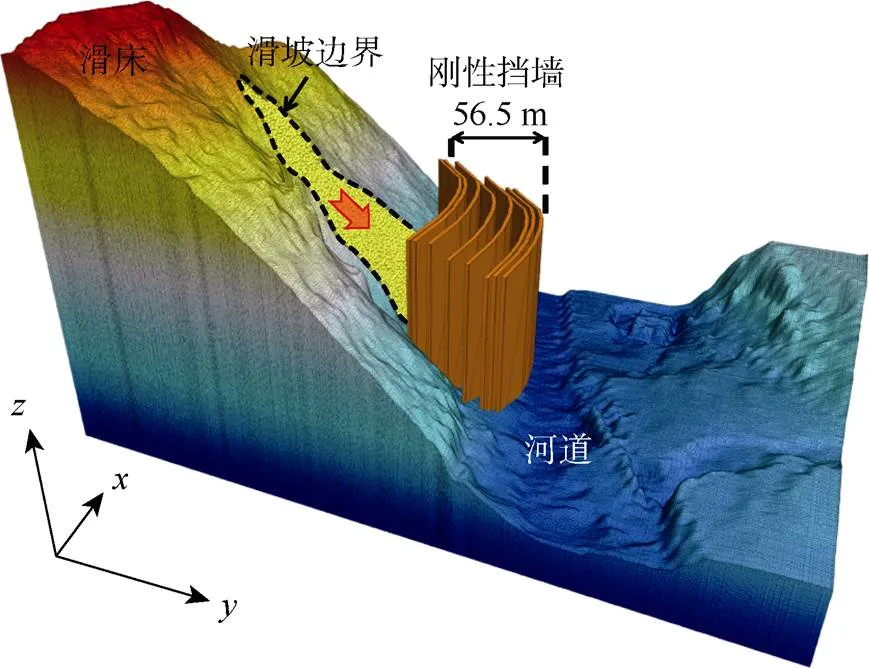
图12 挡墙冲击力测试数值模型

图13 不同坡脚距处滑坡冲击力随时间的变化曲线

通过对不同坡脚距处初始碰撞阶段的最大冲击力(local max)和静止土压力(s)进行统计和分析，得到初始最大值local max、静止土压力s分别与坡脚距i之间的关系，如图14所示，式中0≤i≤56.5 m。

图14中关系式表明，以冲击力指标所表征的马边滑坡致灾强度大小随着滑坡在水平地面运动距离的增大而减小，并在运动停止前呈现出指数衰减的特征。local max随着i的增大而减小程度要比s显著。

从滑坡破坏及运动过程分析可知，当滑坡体在整体发生破坏并沿滑面运移到斜坡坡脚时，由于具有较大的体积和速度，因而在坡脚处具有最大的冲击力强度，随着滑坡体与水平地面的碰撞、摩擦运动等，滑坡内部能耗与地面之间的摩擦能耗增加，导致滑坡土体颗粒运动速度变缓，冲击力减小，滑坡冲击强度也随之降低。

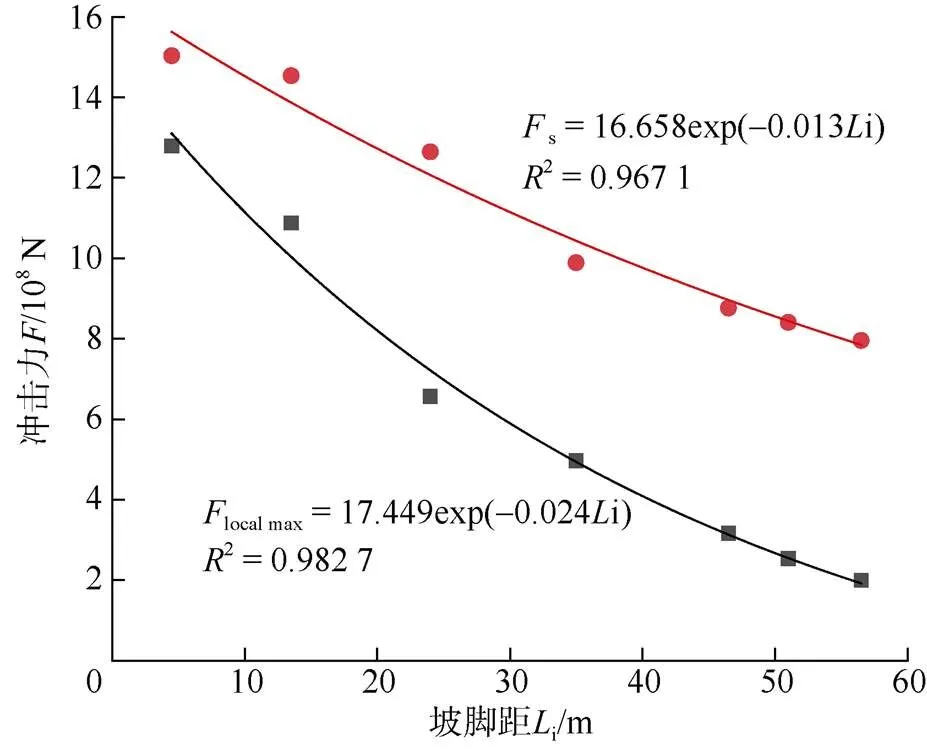
图14 马边滑坡冲击力随坡脚距的变化曲线

4 结论

a. 基于SVM和PFC方法能够快速、有效地学习和标定，获取滑坡岩土体的摩擦角、黏聚力等强度参数，并与室内三轴试验结果进行对比，其结果满足模拟要求。

b. 根据滑坡反演分析结果，滑坡中后部颗粒运动迹线基本为直线型，滑坡中前部滑体颗粒运移至河谷处呈扇形堆积特征，且模拟滑坡堆积形态与其真实堆积特征基本一致。

c.滑坡运动总时长约32 s，运动开始5 s后速度达到峰值10.2 m/s，运动冲击后不同滑坡坡脚距处的最大冲击力和最终土压力均随着坡脚距的增大而呈现出指数衰减特征，且随着坡脚距的增大，最大冲击力比静止土压力衰减更加显著。

[1] 胡晓波，樊晓一，唐俊杰. 基于离散元的高速远程滑坡运动堆积特征及能量转化研究：以三溪村滑坡为例[J]. 地质力学学报，2019，25(4)：527–535.

HU Xiaobo，FAN Xiaoyi，TANG Junjie. Accumulation characteristics and energy conversion of high-speed and long-distance landslide on the basis of DEM：A case study of Sanxicun landslide[J]. Journal of Geomechanics，2019，25(4)：527–535.

[2] LO Chiaming，LEE Chingfang，HUANG Weikai. Failure mechanism analysis of rainfall-induced landslide at Pingguang stream in Taiwan：Mapping，investigation，and numerical simulation[J]. Environmental Earth Sciences，2016，75(21)：1–20.

[3] SHI Chong，LI Dejie，CHEN Kaihua，et al. Failure mechanism and stability analysis of the Zhenggang landslide in Yunnan Province of China using 3D particle flow code simulation[J]. Journal of Mountain Science，2016，13(5)：891–905.

[4] TANG Chaolung，HU Jyrching，LIN Minglang，et al. The Tsaoling landslide triggered by the Chi-Chi earthquake，Taiwan：Insights from a discrete element simulation[J]. Engineering Geology，2009，106(1/2)：1–19.

[5] 陈达，薛喜成，魏江波. 基于PFC2D的刘涧滑坡破坏运动过程模拟[J]. 煤田地质与勘探，2018，46(4)：115–121.

CHEN Da，XUE Xicheng，WEI Jiangbo. Simulation of failure process of Liujian landslide based on PFC2D[J]. Coal Geology & Exploration，2018，46(4)：115–121.

[6] LO Chiaming，LIN Minglang，TANG Chaolung，et al. A kinematic model of the Hsiaolin landslide calibrated to the morphology of the landslide deposit[J]. Engineering Geology，2011，123(1/2)：22–39.

[7] 周礼，范宣梅，许强，等. 金沙江白格滑坡运动过程特征数值模拟与危险性预测研究[J]. 工程地质学报，2019，27(6)：1395–1404.

ZHOU Li，FAN Xuanmei，XU Qiang，et al. Numerical simulation and hazard prediction on movement process characteristics of Baige landslide in Jinsha river[J]. Journal of Engineering Geology，2019，27(6)：1395–1404．

[8] ZOU Zongxing，TANG Huiming，XIONG Chengren，et al. Kinetic characteristics of debris flows as exemplified by field investigations and discrete element simulation of the catastrophic Jiweishan rockslide，China[J]. Geomorphology，2017，295：1–15.

[9] LI Bin，XING Aiguo，XU Chong. Simulation of a long-runout rock avalanche triggered by the Lushan earthquake in the Tangjia Valley，Tianquan，Sichuan，China[J]. Engineering Geology，2017，218(29)：107–116.

[10] GAO Ge，MEGUID M A. On the role of sphericity of falling rock clusters-insights from experimental and numerical investigations[J]. Landslides，2018，15(2)：219–232.

[11] BI Yuzhang，HE Siming，DU Yanjun，et al. Effects of the configuration of a baffle-avalanche wall system on rock avalanches in Tibet Zhangmu：Discrete element analysis[J]. Bulletin of Engineering Geology and the Environment，2019，78：2267–2282.

[12] 杨帆，许强，范宣梅，等. 基于时间序列与人工蜂群支持向量机的滑坡位移预测研究[J]. 工程地质学报，2019，27(4)：880–889．

YANG Fan，XU Qiang，FAN Xuanmei，et al. Prediction of landslide displacement time series based on support vector regression machine with Artificial Bee Colony algorithm[J]. Journal of Engineering Geology，2019，27(4)：880–889．

[13] 谭龙，陈冠，王思源，等. 逻辑回归与支持向量机模型在滑坡敏感性评价中的应用[J]. 工程地质学报，2014，22(1)：56–63.

TAN Long，CHEN Guan，WANG Siyuan，et al. Landslide susceptibility mapping based on Logistic Regression and Support Vector Machine[J]. Journal of Engineering Geology，2014，22(1)：56–63.

[14] 罗战友，杨晓军，龚晓南. 基于支持向量机的边坡稳定性预测模型[J]. 岩石力学与工程学报，2005，24(1)：144–148.

LUO Zhanyou，YANG Xiaojun，GONG Xiaonan. Support Vector Machine model in slope stability evaluation[J]. Chinese Journal of Rock Mechanics and Engineering，2005，24(1)：144–148.

[15] 周超，殷坤龙，曹颖，等. 基于诱发因素响应与支持向量机的阶跃式滑坡位移预测[J]. 岩石力学与工程学报，2015，34(增刊2)：4132–4139.

ZHOU Chao，YIN Kunlong，CAO Ying，et al. Displacement prediction of step-like landslide based on the response of inducing factors and Support Vector Machine[J]. Chinese Journal of Rock Mechanics and Engineering，2015，34(Sup.2)：4132–4139.

[16] 孙明志，戴文亭，孙思博，等. 基于GA–SVM岩土参数反演的改进PBA工法研究[J]. 地下空间与工程学报，2020，16(4)：1163–1171.

SUN Mingzhi，DAI Wenting，SUN Sibo，et al. Research on the improvement of PBA construction method based on GA-SVM[J]. Chinese Journal of Underground Space and Engineering，2020，16(4)：1163–1171.

[17] MA Siyuan，XU Chong，SHAO Xiaoyi，et al. Geometric and kinematic features of a landslide in Mabian Sichuan，China，derived from UAV photography[J]. Landslides，2018，16(2)：373–381.

[18] 曹文，李维朝，唐斌，等. PFC滑坡模拟二、三维建模方法研究[J]. 工程地质学报，2017，25(2)：455–462.

CAO Wen，LI Weichao，TANG Bin，et al. PFC study on building of 2D and 3D landslide models[J]. Journal of Engineering Geology，2017，25(2)：455–462.

[19] WEI Jiangbo，ZHAO Zhou，XU Chong，et al. Numerical investigation of landslide kinetics for the recent Mabian landslide(Sichuan，China)[J]. Landslides，2019，16(11)：2287–2298.

[20] SCHEIDEGGER A E. On the prediction of the reach and velocity of catastrophic landslides：2F，1T，14R. ROCK MECHANICS，V5，N4，1973，P231–236[J]. International Journal of Rock Mechanics & Mining Sciences & Geomechanics Abstracts，1974，11(3)：65.

[21] 吴越，刘东升，李明军. 岩体滑坡冲击能计算及受灾体易损性定量评估[J]. 岩石力学与工程学报，2011，30(5)：901–909.

WU Yue，LIU Dongsheng，LI Mingjun. Impact energy calculation for rock slope and quantitative assessment of vulnerability for element at risk[J]. Chinese Journal of Rock Mechanics and Engineering，2011，30(5)：901–909.

[22] 张志东，樊晓一，姜元俊. 岩土体颗粒级配对滑坡碎屑流冲击力力链特征的影响[J]. 山地学报，2020，38(3)：402–415.

ZHANG Zhidong，FAN Xiaoyi，JIANG Yuanjun. Effect of granularity of rock and soil mass on regularity of impact force chain in a fluidized landslide[J]. Mountain Research，2020，38(3)：402–415.

Numerical study of Mabian landslide kinematics and impact intensity

CHEN Xing1, ZHAO Zhou1, WEI Jiangbo1, XU Chong2

(1. College of Geology and Environment, Xi’an University of Science and Technology, Xi’an 710054, China；2. National Institute of Natural Hazards, Ministry of Emergency Management of China, Beijing 100085, China)

study of landslide kinematics and impact intensity is of great significance for quantitative assessment of landslide risk. In this paper, the basic characteristics of Mabian landslide(occurred on May 5, 2018) in Leshan City, Sichuan Province were investigated. The support vector machine(SVM) model and particle flow method(PFC) were used to calibrate the meso-strength parameters of landslide rock and soil. Combined with the UAV data, the high-precision DEM of landslide area was generated. On this basis, the three-dimensional PFC model of Mabian landslide was reconstructed and simulated. The movement, accumulation and impact process of landslide are studied. The results show that: the movement of Mabian landslide lasted 32 seconds, main sliding time is 16 seconds, and the peak velocity is 10.2 m/s after 5 seconds; the movement trace of rock and soil in the middle and rear of the landslide is linear, while the middle and front of the landslide is in a diffusion state, and finally in a fan-shaped accumulation; the impact force of the landslide at the slope foot can reach 1.5×109N, and the impact force presents the exponential attenuation characteristicswith the increase of the movement distance. The results are basically consistent with the actual video interpretation results of landslide movement and accumulation, and the related research methods could provide references for quantitative risk assessment of landslide.

Mabian landslide; Support Vector Machine(SVM); Particle Flow Code(PFC); landslide kinematics; impact intensity

P642

A

1001-1986(2021)04-0234-08

2021-01-31；

2021-06-09

国家自然科学基金项目(41661144037，41302276)；国家重点研发计划课题(2017YFB0504104)

陈兴，1995年生，男，陕西西安人，硕士研究生，从事地质灾害风险评价研究. E-mail：695395874@qq.com

赵洲，1978年生，男，宁夏隆德人，博士，副教授，从事地质环境调查评价相关研究. E-mail：594682159@qq.com

陈兴，赵洲，魏江波，等. 马边滑坡运动特征及冲击强度的数值研究[J]. 煤田地质与勘探，2021，49(4)：234–241. doi: 10.3969/j.issn.1001-1986.2021.04.028

CHEN Xing，ZHAO Zhou，WEI Jiangbo，et al. Numerical study of Mabian landslide kinematics and impact intensity[J]. Coal Geology & Exploration，2021，49(4)：234–241. doi: 10.3969/j.issn.1001-1986.2021.04.028

(责任编辑 周建军)