基于PSO-BP神经网络的导水裂隙带高度预测

娄高中，谭 毅

基于PSO-BP神经网络的导水裂隙带高度预测

娄高中1，谭 毅2,3

(1. 安阳工学院 土木与建筑工程学院，河南 安阳 455000；2. 河南理工大学 能源科学与工程学院，河南 焦作 454003；3. 煤炭安全生产与清洁高效利用省部共建协同创新中心，河南 焦作 454003)

导水裂隙带高度是西部矿区保水采煤的理论依据和关键参数。近年来，BP神经网络广泛应用于导水裂隙带高度预测，但BP神经网络存在收敛速度慢、易陷入局部极小等问题。为提高导水裂隙带高度预测的准确性，利用粒子群优化算法(PSO)对BP神经网络的权值和阈值进行优化，建立基于PSO-BP神经网络的导水裂隙带高度预测模型。选择开采厚度、开采深度、工作面倾斜长度、煤层倾角、覆岩结构特征为导水裂隙带高度主要影响因素，选取22例导水裂隙带高度实测数据对PSO-BP神经网络进行训练，将训练后的PSO-BP神经网络对2例测试样本的预测结果与实际值进行对比，并与BP神经网络预测模型及经验公式预测结果进行对比。结果表明：PSO-BP神经网络预测模型的平均相对误差为1.55%；BP神经网络预测模型的平均相对误差为4.8%，经验公式的最小相对误差为9.4%，PSO-BP神经网络预测精度明显优于BP神经网络和经验公式，且绝对误差和相对误差变化较稳定，可以有效预测导水裂隙带高度。

粒子群优化算法；BP神经网络；导水裂隙带高度；影响因素；预测模型

随着我国能源消费结构的逐年优化，2020年煤炭在能源消费中的比例下降到56.7%。但原煤产量较2019年增长0.9%，达到38.4亿t，在当前及未来一段时间内煤炭依然是我国的主体能源。随着我国中东部矿区浅部煤炭资源的逐年枯竭与开采深度及难度的增加，我国煤炭资源开采的重心已转向西部。西部主要矿区位于黄河流域的干旱半干旱地区，水资源匮乏，年蒸发量数倍于年降水量，且煤炭高强度开采不可避免地破坏水资源。为实现煤炭资源开采与水资源承载能力间的平衡，必须进行保水采煤[1]。导水裂隙带高度是保水采煤的理论依据和关键参数，因此，准确预测导水裂隙带高度对于西部矿区煤炭资源开采以及水资源保护具有重要意义[2-3]。

目前，国内外学者主要采用经验公式[4-5]、理论分析[6-7]、数值模拟与相似模拟[8]、现场实测[9-10]等方法对导水裂隙带高度进行研究。导水裂隙带高度影响因素较多，具有复杂、难定量、非线性的特点，BP神经网络具有自学习和自适应、较强的非线性映射能力和泛化能力等优点，李振华等[11]、施龙青等[12]建立了基于BP神经网络的导水裂隙带高度预测模型，取得了较好的预测结果。但BP神经网络存在收敛速度慢、易陷入局部极小等问题，对导水裂隙带高度预测精度有一定影响。

粒子群优化算法(Particle Swarm Optimization，PSO)是基于群体智能的优化算法，算法结构简单，易于实现，具有良好的全局寻优能力，在各种工程中广泛应用。邵良杉等[13]采用PSO优化最小二乘支持向量机(LSSVM)的核函数和正则化参数，建立了瓦斯渗透率的PSO-LSSVM预测模型，取得较高精度的预测结果；毛志勇等[14]采用自适应粒子群优化算法(APSO)优化加权最小二乘支持向量机(WLS- SVM)的组合参数(、)，建立含瓦斯煤渗透率的APSO-WLS-SVM预测模型，预测精度优于WLS- SVM预测模型。

考虑到BP神经网络存在的问题，笔者利用PSO良好的全局寻优能力对BP神经网络的权值与阈值进行优化，建立导水裂隙带高度与开采厚度、开采深度、工作面倾斜长度、煤层倾角、覆岩结构特征等主要影响因素间的PSO-BP神经网络预测模型，以期提高导水裂隙带高度预测准确性。

1 PSO-BP神经网络模型

1.1 BP神经网络

BP神经网络是一种按误差逆向传播算法训练的多层前馈网络，是应用最广泛的神经网络模型之一。BP神经网络拓扑结构包括输入层、隐含层和输出层。单隐含层的BP神经网络可以实现以任意精度近似非连续函数，因此，本文拟采用单隐含层的BP神经网络。

BP神经网络包括数据的前向传播和误差的反向传播2个过程，当输出层结果与期望结果有差别时，则进行误差信号的反向传播，通过2个过程的反复迭代，使网络的输出接近期望输出。

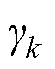
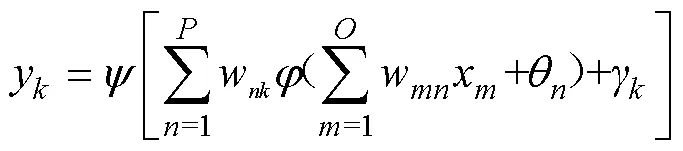
误差的反向传播是从输出层开始逐层计算各层神经元的输出误差，根据梯度下降法，按误差函数的负梯度方向修正隐含层与输出层的权值与阈值[16]，使修正后的网络最终输出尽可能接近期望输出。

1.2 粒子群优化算法

粒子群优化算法(PSO)是由J. Kennedy和R. C. Eberhart提出的一种群体智能算法[17]。PSO首先在可行解空间初始化一定种群规模的粒子以及每个粒子的位置和速度，每个粒子对应待求问题的一个潜在最优解，并根据适应度函数确定其适应度；粒子在解空间中进行迭代搜索时跟踪2个极值，一个是粒子自身搜索到的最优解，称为个体极值，另一个是粒子群体目前搜索到的最优解，称为全局极值；之后粒子更新自身的速度和位置，直至搜索到全局最优解或达到最大迭代次数，算法结束。

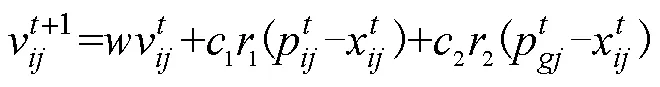
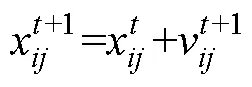
式(2)中粒子速度更新由3部分组成，第1部分表示自身先前速度；第2部分表示粒子个体的认知能力，即向个体最优解逼近的趋势；第3部分表示粒子间的信息共享和合作，即向群体最优解逼近的趋势。其中第1部分中惯性权重决定粒子先前速度对当前速度的影响，较大时，粒子能在全局范围搜索到较优值，全局收敛性能强；较小时，粒子能在全局较优值附近范围精细搜索，局部收敛性能强。为实现PSO全局收敛性能与局部收敛性能之间的平衡，可以对进行动态调整。目前应用广泛的是线性递减策略[13]，如下式：

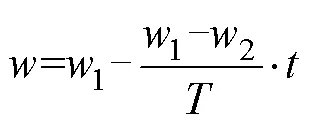
式中：1为初始权重；2为终止权重；为最大迭代次数。

1.3 PSO-BP神经网络

PSO-BP神经网络实质是将BP神经网络的权值和阈值映射为PSO粒子，通过对粒子速度和位置的更新迭代优化权值和阈值，从而提高BP神经网络的收敛速度和预测精度。PSO-BP神经网络预测的具体步骤如下：

①初始化BP神经网络和粒子群优化算法参数根据样本数据，确定BP神经网络输入层、隐含层、输出层的节点个数、、；设置粒子群种群规模，学习因子1、2，最大迭代次数，初始权重与终止权重1、2。

②建立BP神经网络权值、阈值与PSO中粒子维数的映射关系 对于单隐含层的BP神经网络，粒子的维数=×+×++。

③计算适应度 种群粒子的优劣由适应度函数确定，适应度函数采用BP神经网络实际输出与期望输出间的均方误差平方和表示。

④更新个体极值与全局极值 根据适应度函数，比较粒子当前与上一时刻的适应度值，如果当前适应度更好，进行个体极值的更新；同样，比较粒子群体当前与上一时刻的适应度值，如果优于上一时刻，进行全局极值的更新。

⑤粒子速度与位置的更新 根据式(2)、式(3)更新粒子速度和位置。

⑥判断PSO算法是否满足结束条件如果PSO算法达到最大迭代次数或误差小于期望误差，算法结束，输出最优解；如不满足，返回步骤③。

⑦将最优解赋给BP神经网络的权值和阈值利用PSO优化后的权值与阈值，进行BP神经网络的训练与预测。

PSO-BP神经网络预测流程如图1所示。

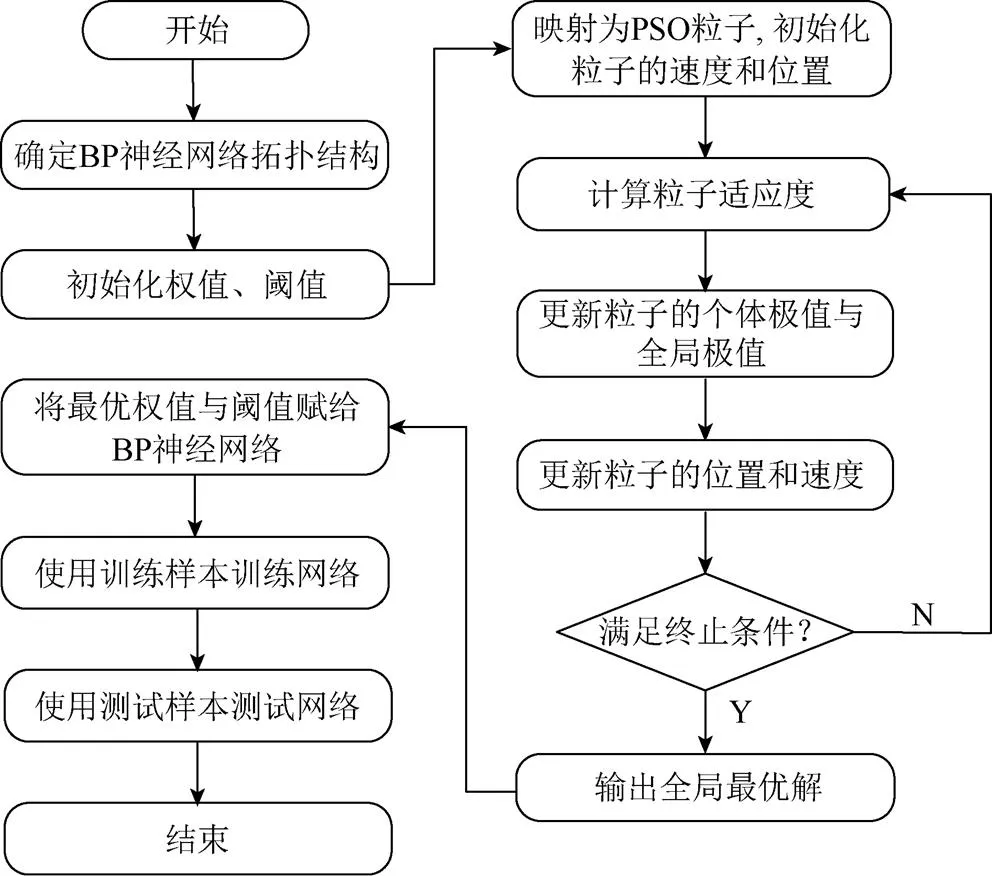
图1 PSO-BP神经网络流程

2 基于PSO-BP神经网络的导水裂隙带高度预测模型建立及分析

2.1 导水裂隙带高度主要影响因素与样本数据

1)开采厚度

一般情况下，当其他因素一定时，开采厚度越大，导水裂隙带高度越大，与开采厚度近似呈线性或分式函数关系[11]。王晓振等[19]认为在关键层控制作用下，导水裂隙带高度随开采厚度的增加呈台阶式突变，当关键层控制的岩层厚度越大，台阶突变越明显；当开采厚度的增加不超过导水裂隙带高度产生台阶落差范围时，导水裂隙带高度不随着开采厚度的增加而增加。

2) 开采深度

煤层开采后，上覆岩层在矿山压力作用下产生移动和破坏，从而形成导水裂隙带。根据矿压理论，煤层开采深度为25～2 700 m时，矿山压力随着开采深度的增大而增加，上覆岩层移动和破坏程度越剧烈，导水裂隙带高度发育越大[7]。

抽滤阶段：在消化残渣中加入25 ml 20%磺基水杨酸，在室温放置30 min，将烧杯中的残留物进行真空抽滤，最终将酶解液定容，并测定还原糖含量。

3) 工作面倾斜长度

对于我国广泛应用的走向长壁开采工作面，在覆岩破坏未达到充分采动时，导水裂隙带高度随工作面倾斜长度的增加呈台阶状或分式函数增长，当工作面倾斜长度达到该地质采矿条件下的临界长度时，覆岩破坏达到充分采动，导水裂隙带高度不再受工作面倾斜长度的影响[20]。

4)煤层倾角

随着煤层倾角的增大，导水裂隙带在倾斜方向上的形态由马鞍形向抛物线形和椭圆形转变，同时影响导水裂隙带高度，当煤层倾角小于45°时，导水裂隙带高度随着煤层倾角增大而增大，当煤层倾角为45°～60°时，导水裂隙带高度随倾角的增大而减小[21]。

5)覆岩结构特征

上覆岩层具有分层特征，根据上覆岩层的岩性，按从直接顶到基本顶的顺序，覆岩结构特征可以分为坚硬–坚硬、坚硬–软弱、软弱–坚硬、软弱–软弱4种类型。坚硬–坚硬型覆岩下沉量小，垮落空间几乎全靠垮落岩块碎胀充填，垮落过程发育最充分，而且覆岩断裂后不易闭合和恢复隔水能力，导水裂隙带高度发育最大；软弱–软弱型覆岩随采随垮，垮落过程发育最不充分，导水裂隙带高度发育最小；一般情况下，软弱–坚硬型覆岩较坚硬–软弱型覆岩垮落过程充分。因此，导水裂隙带高度由小至大对应的覆岩结构特征为软弱–软弱、坚硬–软弱、软弱–坚硬、坚硬–坚硬，在定量分析中分别量化取值0.2、0.4、0.6、0.8[11]。

根据选择的导水裂隙带高度主要影响因素，收集了国内部分矿区导水裂隙带高度实测样本数据[4,22-24]，见表1。

2.2 PSO-BP神经网络参数确定

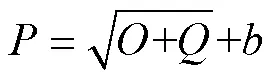
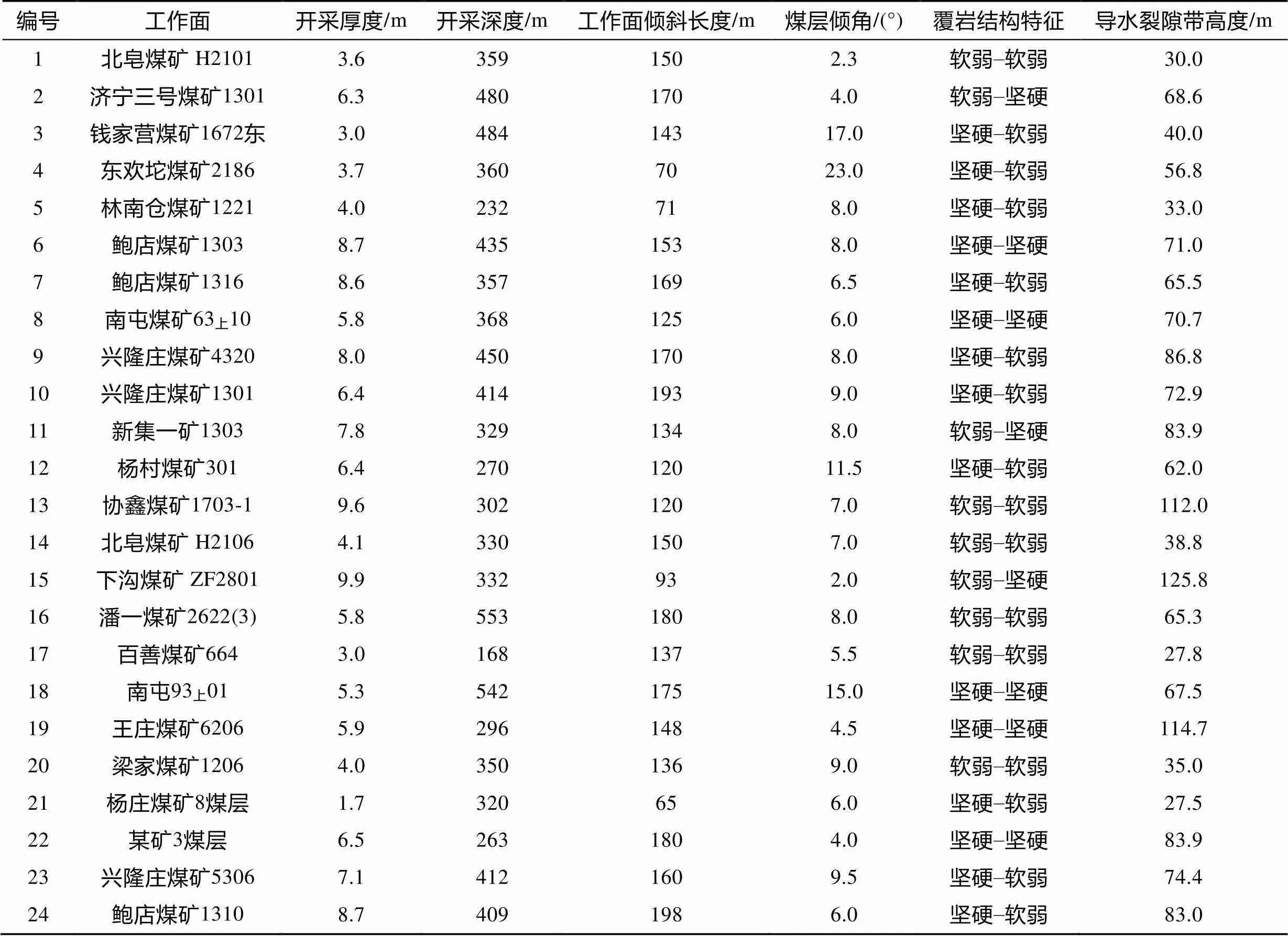
表1 导水裂隙带高度实测样本数据

根据BP神经网络的拓扑结构，PSO的维数=5×10+10×1+10+1=71；种群规模较小时，算法收敛速度快，较大时，算法寻优能力好，但收敛速度慢，一般情况下取值10～50，本次种群规模=30；初始权重1和终止权重2分别为0.9、0.4；学习因子1=2=1.49；最大迭代次数=100。

2.3 PSO-BP神经网络预测结果及分析

PSO-BP神经网络预测模型建立涉及大量计算，为提高效率，采用Matlab 2014b软件，调用神经网络工具箱函数进行编程。根据已确定的参数，建立基于PSO-BP神经网络的导水裂隙带高度预测模型。

为了保证基于PSO-BP神经网络预测模型的预测能力，将表1中的样本数据分为2类，一类作为训练样本，一类作为测试样本。训练样本和测试样本的个数没有定论，一般情况下，训练样本个数越多，网络的训练能力随之提高，网络预测能力也会提高；测试样本的个数至少为2个[26-27]。基于此，本次选择表1中的前22组数据作为训练样本，对PSO-BP神经网络进行训练；选择后2组数据作为测试样本，用来验证训练后的网络的预测能力。

适应度值是判断预测模型预测结果是否达到预期精度的指标之一[28]。本次适应度函数选择均方误差平方和，如下式：

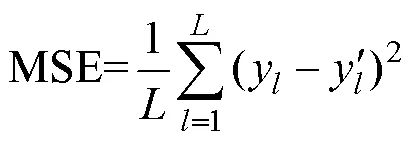
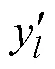
基于PSO-BP神经网络的预测模型的适应度值变化曲线如图2所示。从图2可以看出，随着迭代次数的增加，适应度值从0.45快速下降为0.04，收敛速度快，且PSO-BP神经网络预测模型的预测结果与期望值十分接近，优化效果显著，表明基于PSO-BP神经网络的预测模型是有效可行的。

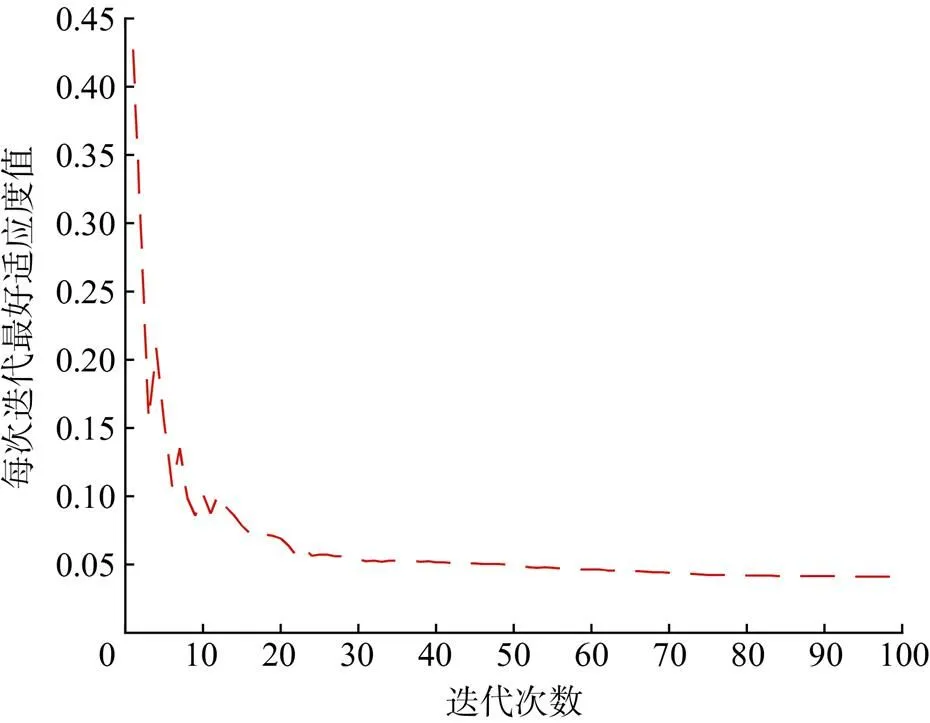
图2 适应度值变化曲线

为定量评价基于PSO-BP神经网络的导水裂隙带高度预测模型的可靠性，采用训练后的PSO-BP神经网络对2个测试样本进行预测，预测结果见表2；然后将预测结果与实际值进行对比，以绝对误差、相对误差2个指标表示，对比结果见表2。

同时，为公平验证基于PSO-BP神经网络的导水裂隙带高度预测模型的优越性，建立基于BP神经网络的预测模型并选择导水裂隙带高度经验公式对测试样本进行预测。其中基于BP神经网络的预测模型的参数与PSO-BP神经网络的相应参数一致；2个测试样本所在工作面采煤方法为综放，覆岩岩性为中硬，导水裂隙带高度经验公式[22]如下：

式中：li为导水裂隙带高度，m；为采高，m。

基于BP神经网络的导水裂隙带高度预测模型和导水裂隙带高度经验公式的预测结果、绝对误差、相对误差见表2。

表2 PSO-BP神经网络、BP神经网络及经验公式预测结果

根据表2中预测结果对比可知：

(1) PSO-BP神经网络预测模型的最大绝对误差为1.6 m，最大相对误差为1.9%；BP神经网络预测模型的最大绝对误差为4.2 m，最大相对误差为5.6%；导水裂隙带高度经验公式的最大绝对误差为101.0 m，最大相对误差达到121.7%，远远大于PSO-BP神经网络与BP神经网络；经验公式最小绝对误差为7.0 m，最小相对误差为9.4%，也明显大于PSO-BP神经网络与BP神经网络。表明PSO-BP神经网络与BP神经网络预测结果相比较经验公式的预测结果均更接近实测值，预测导水裂隙带高度时应尽可能全面考虑其主要影响因素。

(2) PSO-BP神经网络预测模型的平均绝对误差为1.25 m，平均相对误差为1.55%；BP神经网络预测模型的平均绝对误差为3.75 m，平均相对误差为4.8%；PSO-BP神经网络的绝对误差与相对误差均明显优于BP神经网络，且绝对误差与相对误差变化较小。表明经PSO优化后的BP神经网络克服了收敛速度慢、易陷入局部极小的问题，预测准确性大大改善且更加稳定，可以有效预测导水裂隙带高度。

3 结论

a.采用粒子群优化算法(PSO)对BP神经网络的权值与阈值进行优化，根据选取的导水裂隙带高度影响因素以及样本数据，建立基于PSO-BP神经网络的预测模型，解决BP神经网络收敛速度慢、易陷入局部极小等问题，提高了导水裂隙带高度的预测精度。

b.以训练后的PSO-BP神经网络预测模型对测试样本进行预测，预测结果与实际值的平均相对误差为1.55%，BP神经网络预测模型的平均相对误差为4.8%，经验公式的最小相对误差为9.4%。基于PSO-BP神经网络的导水裂隙带高度预测模型准确性高、稳定性好，可有效应用于导水裂隙带高度预测。

[1] 范立民，马雄德，蒋泽泉，等. 保水采煤研究30年回顾与展望[J]. 煤炭科学技术，2019，47(7)：1–30.

FAN Limin，MA Xiongde，JIANG Zequan，et al. Review and thirty years prospect of research on water-preserved coal mining[J]. Coal Science and Technology，2019，47(7)：1–30.

[2] 徐智敏，高尚，崔思源，等. 哈密煤田生态脆弱区保水采煤的水文地质基础与实践[J]. 煤炭学报，2017，42(1)：80–87.

XU Zhimin，GAO Shang，CUI Siyuan，et al. Hydro-geological basic and practice for water-preserved mining in ecologically vulnerable area：A case study in Hami coalfield[J]. Journal of China Coal Society，2017，42(1)：80–87.

[3] 范立民. 保水采煤面临的科学问题[J]. 煤炭学报，2019，44(3)：667–674.

FAN Limin. Some scientific issues in water-preserved coal mining[J]. Journal of China Coal Society，2019，44(3)：667–674.

[4] 娄高中，郭文兵，高金龙. 基于量纲分析的非充分采动导水裂缝带高度预测[J]. 煤田地质与勘探，2019，47(3)：147–153.

LOU Gaozhong，GUO Wenbing，GAO Jinlong. Prediction of the height of water flowing fractured zone under subcritical mining based on dimensional analysis[J]. Coal Geology & Exploration，2019，47(3)：147–153.

[5] 国家安全监管总局，国家煤矿安监局，国家能源局，等. 建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规范[M]. 北京：煤炭工业出版社，2017.

State Administration of Work Safety，National Coal Mine Safety Administration，National Energy Administration，et al. Specifications for coal pillar retention and compressed coal mining in buildings，water bodies，railways and main shafts[M]. Beijing：China Coal Industry Publishing House，2017.

[6] 许家林，朱卫兵，王晓振. 基于关键层位置的导水裂隙带高度预计方法[J]. 煤炭学报，2012，37(5)：762–769.

XU Jialin，ZHU Weibing，WANG Xiaozhen. New method to predict the height of fractured water-conducting zone by location of key strata[J]. Journal of China Coal Society，2012，37(5)：762–769.

[7] 施龙青，辛恒奇，翟培合，等. 大采深条件下导水裂隙带高度计算研究[J]. 中国矿业大学学报，2012，41(1)：37–41.

SHI Longqing，XIN Hengqi，ZHAI Peihe，et al. Calculating the height of water flowing fracture zone in deep mining[J]. Journal of China University of Mining & Technology，2012，41(1)：37–41.

[8] 徐智敏，孙亚军，高尚，等. 干旱矿区采动顶板导水裂隙的演化规律及保水采煤意义[J]. 煤炭学报，2019，44(3)：767–776.

XU Zhimin，SUN Yajun，GAO Shang，et al. Law of mining induced water conduction fissure in arid mining area and its significance in water-preserved coal mining[J]. Journal of China Coal Society，2019，44(3)：767–776.

[9] 李超峰，虎维岳，王云宏，等. 煤层顶板导水裂缝带高度综合探查技术[J]. 煤田地质与勘探，2018，46(1)：101–107.

LI Chaofeng，HU Weiyue，WANG Yunhong，et al. Comprehensive detection technique for coal seam roof water flowing fractured zone height[J]. Coal Geology & Exploration，2018，46(1)：101–107.

[10] 郭文兵，娄高中，赵保才. 芦沟煤矿软硬交互覆岩放顶煤开采导水裂缝带高度研究[J]. 采矿与安全工程学报，2019，36(3)：519–526.

GUO Wenbing，LOU Gaozhong，ZHAO Baocai. Study on the height of water-conductive fracture zone in alternate overburden of soft and hard with top coal caving mining in Lugou coal mine[J]. Journal of Mining & Safety Engineering，2019，36(3)：519–526.

[11] 李振华，许延春，李龙飞，等. 基于BP神经网络的导水裂隙带高度预测[J]. 采矿与安全工程学报，2015，32(6)：905–910.

LI Zhenhua，XU Yanchun，LI Longfei，et al. Forecast of the height of water flowing fractured zone based on BP neural networks[J]. Journal of Mining & Safety Engineering，2015，32(6)：905–910.

[12] 施龙青，黄纪云，韩进，等. 导水裂隙带高度预测的PCA-BP模型[J]. 中国科技论文，2019，14(5)：471–475.

SHI Longqing，HUANG Jiyun，HAN Jin，et al. PCA-BP model for height prediction of water conducting fracture zone[J]. China Science paper，2019，14(5)：471–475.

[13] 邵良杉，马寒. 煤体瓦斯渗透率的PSO-LSSVM预测模型[J]. 煤田地质与勘探，2015，43(4)：23–26.

SHAO Liangshan，MA Han. Model of coal gas permeability prediction based on PSO-LSSVM[J]. Coal Geology & Exploration，2015，43(4)：23–26.

[14] 毛志勇，黄春娟，路世昌，等. 基于APSO-WLS-SVM的含瓦斯煤渗透率预测模型[J]. 煤田地质与勘探，2019，47(2)：66–71.

MAO Zhiyong，HUANG Chunjuan，LU Shichang，et al. Model of gas-bearing permeability prediction based on APSO- WLS-SVM[J]. Coal Geology & Exploration，2019，47(2)：66–71.

[15] 温正，孙华克. MATLAB智能算法[M]. 北京：清华大学出版社，2017.

WEN Zheng，SUN Huake. MATLAB smart algorithm[M]. Beijing：Tsinghua University Press，2017.

[16] 吕伟才，黄晖，池深深，等. 概率积分预计参数的神经网络优化算法[J]. 测绘科学，2019，44(9)：35–41.

LYU Weicai，HUANG Hui，CHI Shenshen，et al. Neural network optimization algorithm for the prediction parameters of probability integral method[J]. Science of Surveying and Mapping，2019，44(9)：35–41.

[17] 钱锋. 粒子群算法及其工业应用[M]. 北京：科学出版社，2013.

QIAN Feng. Particle swarm algorithm and its industrial application[M]. Beijing：Science Press，2013.

[18] 王雨虹，刘璐璐，付华，等. 基于改进BP神经网络的煤矿冲击地压预测方法研究[J]. 煤炭科学技术，2017，45(10)：36–40.

WANG Yuhong，LIU Lulu，FU Hua，et al. Study on predicted method of mine pressure bump based on improved BP neural network[J]. Coal Science and Technology，2017，45(10)：36–40.

[19] 王晓振，许家林，韩红凯，等. 顶板导水裂隙高度随采厚的台阶式发育特征[J]. 煤炭学报，2019，44(12)：3740–3749.

WANG Xiaozhen，XU Jialin，HAN Hongkai，et al. Stepped development characteristic of water flowing fracture height with variation of mining thickness[J]. Journal of China Coal Society，2019，44(12)：3740–3749.

[20] 郭文兵，娄高中. 覆岩破坏充分采动程度定义及判别方法[J]. 煤炭学报，2019，44(3)：755–766.

GUO Wenbing，LOU Gaozhong. Definition and distinguishing method of critical mining degree of overburden failure[J]. Journal of China Coal Society，2019，44(3)：755–766.

[21] 尹尚先，徐斌，徐慧，等. 综采条件下煤层顶板导水裂缝带高度计算研究[J]. 煤炭科学技术，2013，41(9)：138–142.

YIN Shangxian，XU Bin，XU Hui，et al. Study on height calculation of water conducted fractured zone caused by fully mechanized mining[J]. Coal Science and Technology，2013，41(9)：138–142.

[22] 胡炳南，张华兴，申宝宏. 建筑物、水体、铁路及主要井巷煤柱留设与压煤开采指南[M]. 北京：煤炭工业出版社，2017.

HU Bingnan，ZHANG Huaxing，SHEN Baohong. Guidelines for coal pillar retention and compressed coal mining in buildings，water bodies，railways and main shafts[M]. Beijing：China Coal Industry Publishing House，2017.

[23] 王正帅，邓喀中，谭志祥. 导水裂缝带高度预测的模糊支持向量机模型[J]. 地下空间与工程学报，2011，7(4)：723–727.

WANG Zhengshuai，DENG Kazhong，TAN Zhixiang. Height prediction of water fractured zone based on fuzzy SVM[J]. Chinese Journal of Underground Space and Engineering，2011，7(4)：723–727.

[24] 樊振丽. 纳林河复合水体下厚煤层安全可采性研究[D]. 北京：中国矿业大学(北京)，2013.

FAN Zhenli. Mining safety research of thick coal seam under aquifers and surface water in Nalinhe mine area[D]. Beijing：China University of Mining and Technology(Beijing)，2013.

[25] 曹博，白刚，李辉. 基于PCA-GA-BP神经网络的瓦斯含量预测分析[J]. 中国安全生产科学技术，2015，11(5)：84–90.

CAO Bo，BAI Gang，LI Hui. Prediction of gas content based on PCA-GA-BP neural network[J]. Journal of Safety Science and Technology，2015，11(5)：84–90.

[26] 韩亮，刘殿书，李红江，等. 基于Weibull模型的高台阶抛掷爆破爆堆形态BP神经网络预测[J]. 煤炭学报，2013，38(11)：1947–1952.

HAN Liang，LIU Dianshu，LI Hongjiang，et al. BP neural network forecast of blasting muck pile form of high bench cast blasting based on Weibull model[J]. Journal of China Coal Society，2013，38(11)：1947–1952.

[27] 臧子婧，吴海波，张平松，等. 基于ABC-BP模型的煤层含气量预测[J]. 煤田地质与勘探，2021，49(2)：152–158.

ZANG Zijing，WU Haibo，ZHANG Pingsong，et al. Prediction of coal seam gas content based on ABC-BP model[J]. Coal Geology & Exploration，2021，49(2)：152–158.

[28] 宁永香，崔希民. 矿山边坡地表变形的PSO-ELM预测模型[J]. 煤田地质与勘探，2020，48(6)：201–206.

NING Yongxiang，CUI Ximin. PSO-ELM prediction model for surface deformation of mine slope[J]. Coal Geology & Exploration，2020，48(6)：201–206.

Prediction of the height of water flowing fractured zone based on PSO-BP neural network

LOU Gaozhong1, TAN Yi2,3

(1. School of Civil and Architectural Engineering, Anyang Institute of Technology, Anyang 455000, China; 2. School of Energy Science and Engineering, Henan Polytechnic University, Jiaozuo 454003, China; 3. State Collaborative Innovation Center of Coal Work Safety and Clean-Efficiency Utilization, Jiaozuo 454003, China)

Theheight of water flowing fractured zone is the theoretical basis and key parameter of water-preserved mining in western mining areas of China. In recent years, BP neural network has been widely used to predict the height of water flowing fracture zone, but it has such defects as slow convergence speed and a tendency to fall into local minimum. In order to improve the prediction accuracy of the height of water flowing fractured zone, the weight values and thresholds of BP neural network were optimized by particle swarm optimization(PSO), and a prediction model was established based on PSO-BP neural network. Mining thickness, mining depth, inclined length of working face, dip angle of coal seam, overburden structural characteristics were chosen as the main influential factors of the height of water flowing fractured zone, and 22 measured data of the height of water flowing fractured zone were selected to train PSO-BP neural network. Then the trained PSO-BP neural network was used to predict two test samples, and the results were compared with the actual values, and with the predicting results of BP neural network prediction model and empirical formulas. The research results show that the average relative error of PSO-BP neural network prediction model is 1.55%, and that of BP neural network prediction model and the minimum relative error of empirical formulas are 4.8% and 9.4% respectively. The prediction accuracy of PSO-BP neural network is obviously significantly better than BP neural network and empirical formulas, and the variation of its absolute error and relative error are relatively stable, so PSO-BP neural network can effectively predict the height of water flowing fractured zone.

particle swarm optimization; BP neural network; height of water flowing fractured zone; influential factors; prediction model

TD823.83

A

1001-1986(2021)04-0198-07

2021-02-05；

2021-06-09

国家自然科学基金项目(51774111)；河南省科技攻关项目(212102310406)；安阳工学院博士科研基金项目(BSJ2019028)

娄高中，1988年生，男，河南平顶山人，博士，讲师，从事“三下”采煤研究. E-mail：754937725@qq.com

娄高中，谭毅. 基于PSO-BP神经网络的导水裂隙带高度预测[J]. 煤田地质与勘探，2021，49(4)：198–204. doi: 10.3969/j.issn.1001-1986.2021.04.024

LOU Gaozhong，TAN Yi. Prediction of the height of water flowing fractured zone based on PSO-BP neural network[J]. Coal Geology & Exploration，2021，49(4)：198–204. doi: 10.3969/j.issn.1001-1986.2021.04.024

(责任编辑 周建军)