基于主成分分析和最近邻算法的断层识别研究

邹冠贵，任 珂，吉 寅，丁建宇，张少敏

基于主成分分析和最近邻算法的断层识别研究

邹冠贵1,2，任 珂2，吉 寅2，丁建宇2，张少敏2

(1. 中国矿业大学(北京)煤炭资源与安全开采国家重点实验室，北京 100083；2. 中国矿业大学(北京)地球科学与测绘工程学院，北京 100083)

断层是影响煤矿安全的致灾地质因素，查明断层特征是煤矿三维地震勘探的主要目的之一。常规断层解释中采用的人机交互解释方法，其可靠性在一定程度上取决于解释者的经验。为提高断层解释精度，提出一种基于主成分分析和最近邻算法来检测沿目标层断层分布的方法。首先，选择峰峰矿区羊东煤矿作为研究区域，从矿区高精度处理后获得的三维地震数据中提取10个地震属性；然后，采用主成分分析法(PCA)将上述10个地震属性整合为6个综合属性；同时，将属性信息与从矿区15口井和3条巷道确定的139个点的断层信息相结合，构建已知数据信息；在该数据信息的基础上，分别组建出数据集1和数据集2两种数据集，2种数据集的训练集与测试集的比分别为9∶1和3∶7。利用这些数据集以及十折交叉验证的方法，开展基于最近邻算法(kNN)的断层识别准确率测试，数据集1的测试准确率为87.75%，数据集2的测试准确率为71.63%；这表明训练数据量越大，断层识别准确率越高，从而也说明高密度三维地震在该方法的应用中存在一定优势。在对kNN模型的分类性能进行测试时，使用通过PCA进行降维处理的数据作为输入，计算出的分类准确率分别为89.23%和73.79%；这是因为PCA降低了原始输入特征的维数，从而减少了所需的计算量并提高了这些特征的表征能力。综合结果表明，结合PCA和kNN方法可以有效地识别断层分布，减少主观人为因素的影响，提高断层解释的效率。

地震多属性；主成分分析；最近邻算法；断层识别；峰峰矿区羊东煤矿

煤矿开采过程中，断层不仅改变了煤(岩)层的埋藏条件，而且使煤(岩)层错断并发生显著位移，这一方面破坏了煤层的连续性和完整性，为煤层开采带来阻力；另一方面，断层处容易发生瓦斯突出、透水、冒顶等地质灾害，严重影响矿区的安全开采。因此，提前探明矿区断层分布是煤矿安全开采的重要内容。目前，地震领域，断层的解释手段主要是人机交互解释，通过解释人员肉眼观察地震波的振幅、相位和时差等特征以确定断层的存在，解释可靠性在一定程度上取决于解释人员对工区有关褶皱、断裂等构造模式的掌握程度，依靠这种方法解释断层具有很大的局限性，并且是一个费时费力的过程[1]。

为了打破传统断层解释方法的局限性，近年来，不少学者利用属性不连续性来表征断层分布。M. Bahorich等[2]首先提出了相干体属性，并获得了三维数据中地层的不连续性特征；N. M. Albinhassan等[3]将霍夫变换应用于时间切面，以增强断层的显示；S. I. Pedersen等[4]使用蚂蚁跟踪来增强空间不连续性并改善地震数据中的断层特征；F. Admasu等[5]提出了一种用于三维地震数据的半自动断层跟踪方法，该方法涉及使用log-Gabor滤波器来增强断层振幅的不连续性，并在地震剖面上跟踪断层。这些方法通过完善边缘检测属性来增强断层响应，突出显示断层边缘通常取决于属性的质量。Lu Cai等[6]开发了一种体绘制技术，融合体渲染多个地震属性，向解释人员显示了三维数据体内部结构的直观视图；孙振宇等[7]利用支持向量机(Support Vector Machines，简称SVM)进行多属性断层识别。这些研究，通过地震多属性解释很好地避免了对单一属性质量的依赖。在利用多种属性进行地震解释的同时，还需要对其进行数据整合，抓住数据中有效信息，舍弃干扰信息[8-10]。

主成分分析(Principal Component Analysis，简称PCA)是一种使用广泛的数据整合方法，被广泛应用于信号处理、统计等各个领域。这种方法通过分析提取样本的少量特征来降低空间维数，在降维过程中产生的新特征向量为正交向量，向量之间相互独立，可以帮助我们抓住主要信息，尽可能地消除噪声等干扰[11-12]。同时，近年来兴起的机器学习方法具有很好的数据泛化能力，可以从已经得到的数据中获取信息，达到分类或者回归的目的。庞大的地震数据量为机器学习在该领域的应用和发展提供了先决条件[13]。最近邻算法(k-nearest Neighbor Alogorithm，简称kNN)是机器学习领域最常用的算法之一。由于实现简单，理论清晰和分类性能出色，它已在许多领域得到广泛使用[14]。同时，传统的kNN算法需要大量的存储空间对训练样本进行存储，在多维大数据量的情况下，这意味着庞大的运算量和运算时间[15]，经过PCA降维，也很大程度上解决了这方面的不足。

笔者采用PCA方法对多种地震属性进行整合，产生新的综合属性，然后将其作为属性输入并利用kNN算法进行断层识别，同时通过交叉验证评估断层识别的准确率，为地震构造解释的研究提供了一种新的思路。

1 基本原理和方法

1.1 主成分分析(PCA)

主成分分析作为一种常用的线性降维方法，其要求低维子空间对样本具有最大可分性。这种方法最初是由K. Pearson于1901年对非随机变量引入的。1933年，H. Hotelling进一步完善了PCA的数学基础，将其推广到随机向量[16-17]。其核心思想是通过坐标旋转，寻找新的正交基，从而将数据投影到使数据方差最大的维坐标轴上，得到数据在新坐标系中的表示以消除原数据空间的多重共线性，从而达到数据降维的目的[18]。这种方法的主要流程如图1所示。

图1 PCA算法流程

1.2 最近邻算法(kNN)

最近邻算法(k-Nearest Neighbor)是T. Cover和P. Hart于1967年提出一种常用的监督学习算法[20]。kNN的工作机制是：给定测试样本，基于某种距离度量找出训练集中与其最靠近的个训练样本，然后基于这个“邻居”的信息来进行预测。通常，在分类任务中可使用“投票法”，即选择这个样本中出现最多的类别标记作为预测结果。

图2是最近邻算法的原理。从图中可以看出，是一个重要参数，当取值不同时，分类结果会显著不同；另一方面，若采用不同距离的计算方式，则找出的“近邻”可能有显著差别，从而也会导致分类结果的不同[21]。

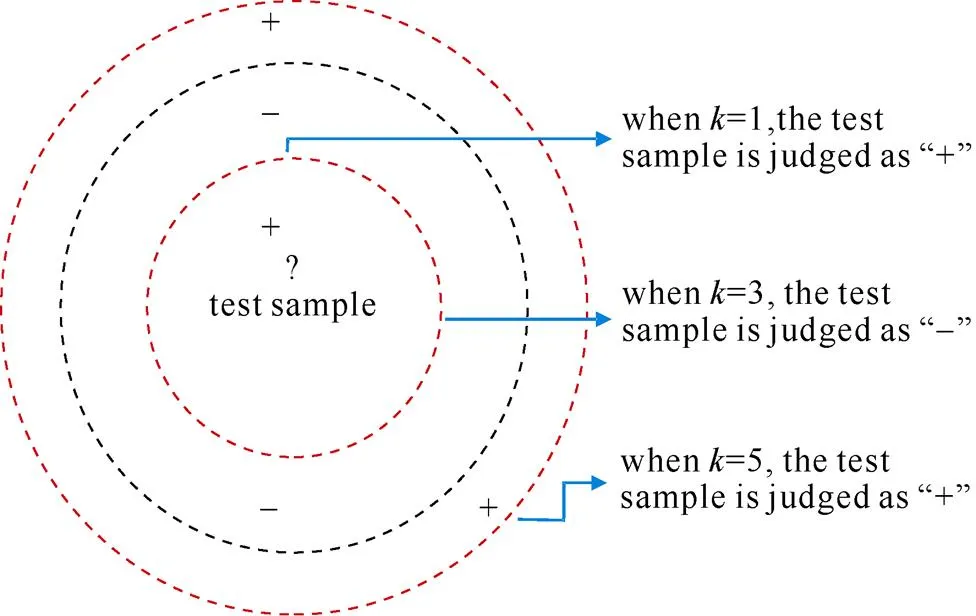
图2 最近邻算法的原理

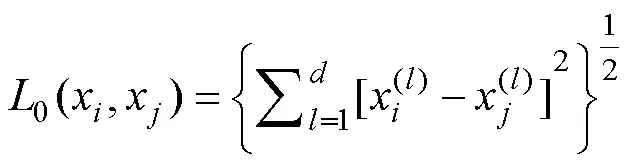
2 数据集构建

2.1 研究区概况

峰峰矿区羊东煤矿位于中国河北邯郸。本矿区内含煤地层为石炭系上统本溪组、石炭–二叠系太原组和二叠系下统山西组，井田含煤地层平均总厚约210 m，含可采煤层6层，即2、4、6、7、8、9号煤，本次研究的目的煤层为2号煤层。2号煤层顶板为粉砂岩，底板为含泥质及炭质粉砂岩，属稳定可采煤层。

研究靶区的勘探面积为3 km2，工作面内已有3条巷道、15口钻井，其在矿区内的分布情况如图3所示。根据巷道和钻井提供的坐标位置与构造特征(是否存在断层)对应关系信息，在2号煤层确定139个点的坐标及该位置所对应的构造特征(表1)。

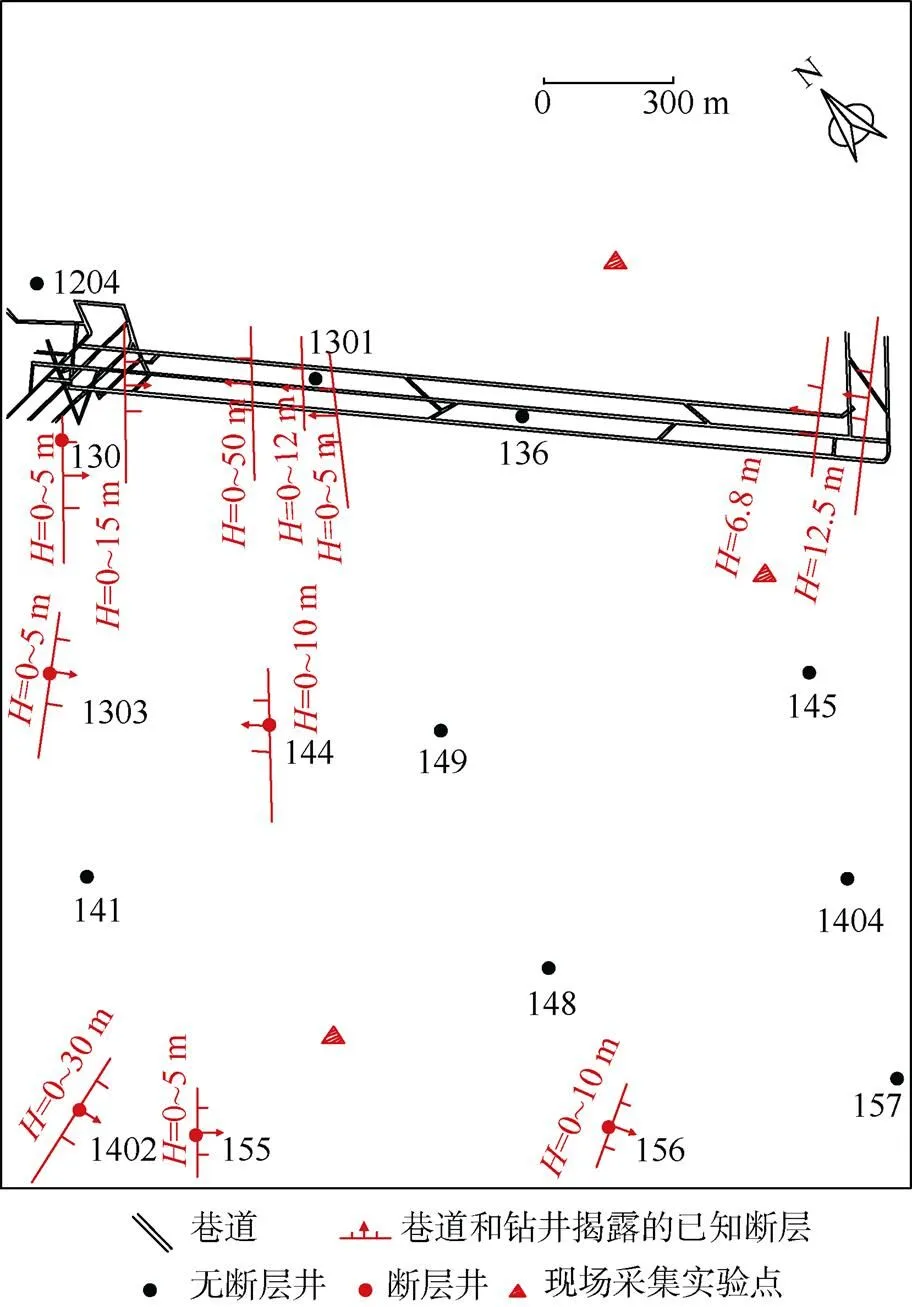
图3 羊东煤矿2号煤层已有钻井、巷道分布情况

2.2 特征提取

特征提取的目的是获取研究对象的尽可能多的信息。地震属性是由叠前或叠后地震数据，经过数学变换而得出的有关地震波的几何学、运动学、动力学或统计学特征，不同的地震属性代表不同的物理特性。因此，地震属性是非常合适的特征提取对象[24]。以方差体为例，方差体的计算是通过求取加权移动的方差值，得到三维数据体中每个时间样点的方差，其计算如式(3)所示。方差值越大，说明相似性越差，常被用于表征地层的不连续变化及检测地下断层。对三维地震数据体提取方差属性，包含了层位不连续信息。

对数据体分别提取了10种地震属性，包括：方差、衰减系数、走向曲率、反射强度、瞬时相位、最大振幅、瞬时频率、倾角偏差、倾角连续性、混沌体，这10种属性均能用于表征断层[7]。然后，将已知构造信息的139个点与提取得到的地震属性根据坐标位置对应起来，构建羊东煤矿2号煤层已知数据集，见表2。其中，非断层数据97组，用标签‘0’表示；断层数据42组，用标签‘1’表示。

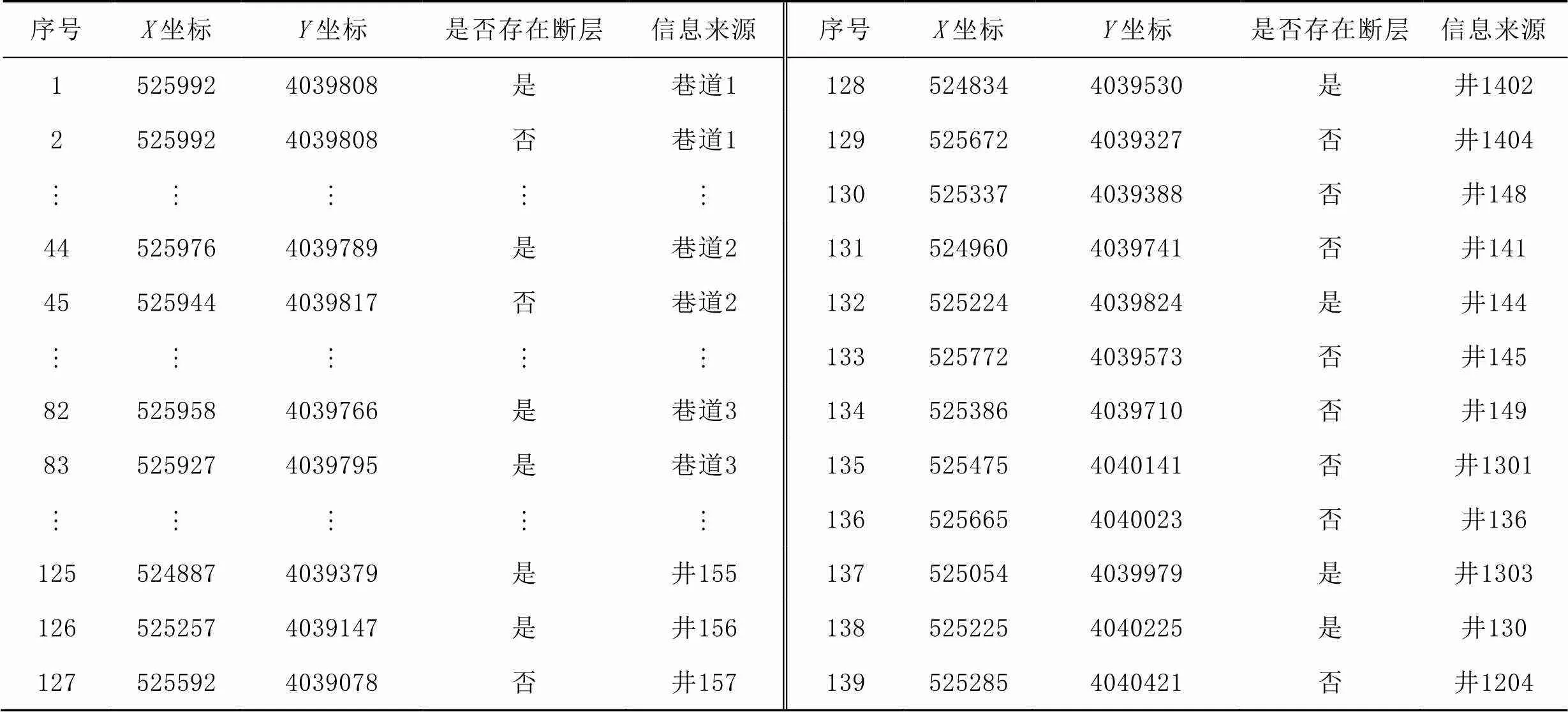
表1 139个点位置坐标及其对应的构造信息

2.3 特征选择

对于从地震数据体提取得到的属性数据集，需要利用PCA对其中的原始地震数据进行整合，整合得到的综合属性将作为特征选择的结果，用于kNN进行断层识别。本文利用SPSS软件对数据进行主成分分析，具体处理过程如下。

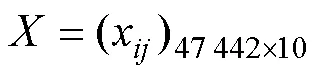
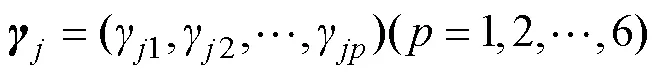
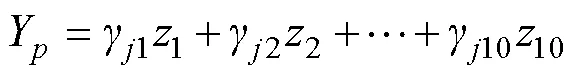
表2 羊东煤矿2号煤层已知数据集

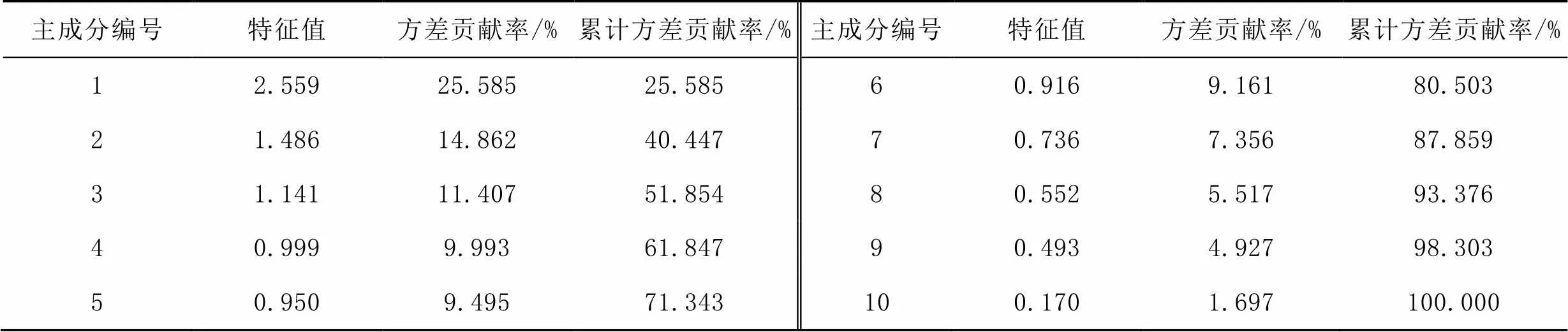
表3 主成分特征值及其方差贡献率

表4 综合属性数据集

3 模型构建与断层自动识别

3.1 交叉验证的思想

在对kNN算法分类准确率进行评估时，通常的方法是将已知数据集随机分为两部分：训练集和测试集。这种方法的样本选取虽然具有随机性，但不同的分类方法训练的结果可能有差异。为了消除这种影响，本文在样本选取时采用了十折交叉验证的方法：将用于分类的139组数据，分成10组，其中每组数据数量如图4所示，每次实验，依次分配训练集9份验证集1份，10次结果的均值作为算法精度的估计[23]。该方法的优点是：所有的样本都进行了训练，每一份样本又各自作为测试集进行验证，提高了预测的精确度；同时，也降低了分组不同的影响。

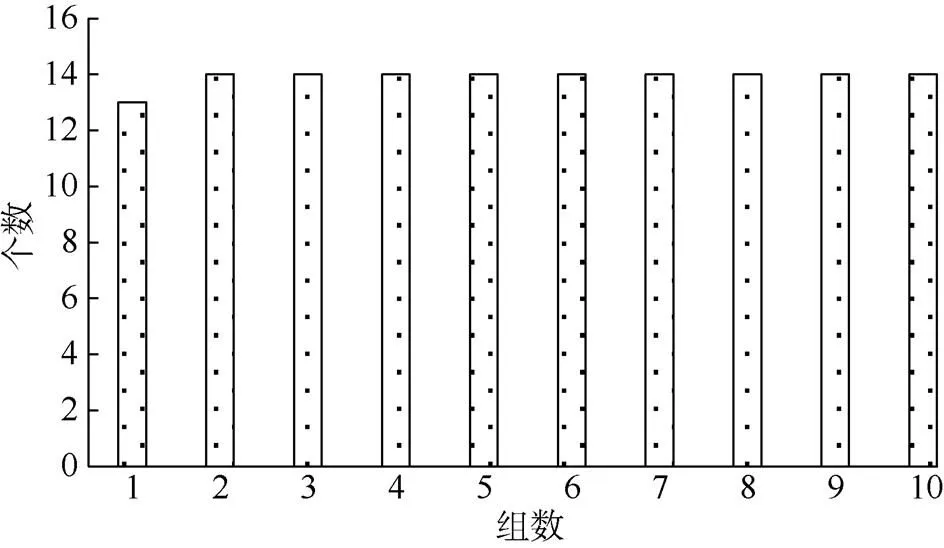
图4 每组数据数量

3.2 模型构建与评估

值的选取是构建kNN分类模型的重要参数，在过拟合和欠拟合之间保持平衡是选择值的关键，值的合理选取可以尽可能减少噪声对输出类别的影响[25]。根据经验规则，一般取奇数且小于训练样本数的平方根，考虑到样本集数据量的大小，本文的取值1、3、5、7、9、11，然后依据验证集准确率大小随取值的变化规律，确定模型的最佳值。

为了更好地观察PCA提取特征前后对kNN分类效果的影响，分别将PCA处理前后的2组数据集作为输入，并利用十折交叉验证的思想和图4的分组方式对2组数据进行分组，然后利用kNN对2组数据进行分类。验证集分类准确率随取值的变化如图5所示。

以分组1为例，从图5中可以看出：在该种分组下，未经过PCA提取主成分的数据集在取值3、5、9、11时，验证集分类准确率最高，为84.61%；同样的分组下，经过PCA提取主成分的数据集在取值1、9、11时，验证集分类准确率最高，为92.31%。同样，其他各组均选择验证集准确率最高时的k值作为当前分组下kNN模型中的最佳取值，并对其对应取值下的验证集准确率进行统计。统计结果显示，未经过PCA选择特征的kNN分类平均准确率为87.75%，经过PCA选择特征的kNN分类平均准确率为89.23%。

为了观察出的取值对分类准确率的影响。对不同分组下同一值的验证集准确率进行统计并求平均值，得到的变化规律曲线如图6中PCA-kNN(a)和kNN(a)所示。从图6中可以看出，当的取值为9时，对应的验证集平均准确率最高，即构建模型最优，是该组数据的最佳值。

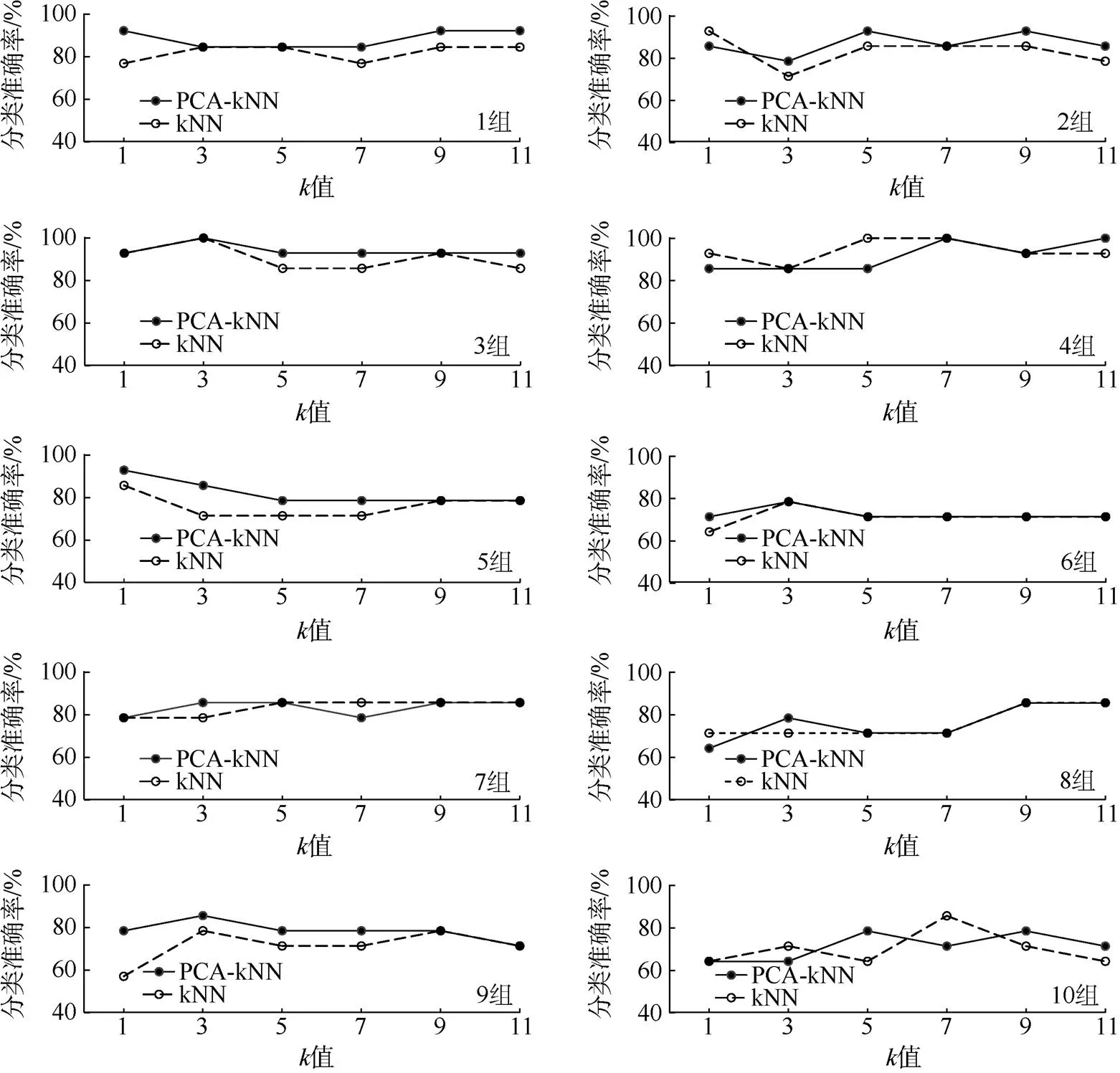
图5 各组验证集分类准确率随k取值的变化

图6 验证集平均准确率随k取值的变化规律

3.3 断层分布预测

利用交叉验证法确定了PCA-kNN的最优参数取值后，对羊东煤矿2号煤层的断层分布进行了预测，预测结果如图7所示。

从图7中可以看出：PCA-kNN预测的断层分布与钻井、巷道揭露的断层分布吻合程度较高，断层走向基本一致，这表明利用PCA-kNN的方法可以实现煤矿断层的分布预测；通过对比可以发现，使用kNN模型获得的断层分布显然比人工断层解释结果更为宽松，这是由于PCA-kNN利用综合属性预测断层区域时，它仅对综合属性值的异常区域产生断层响应，因此，预测结果是相对松散分布的断层点；图中的A处和F处均有断层揭露，人工解释的结果却并未解释出这2个区域的断层，这是因为该处的断层落差较小，地震解释剖面上的断层特征不明显，人工解释常常难以解释出这种落差较小的断层，但是PCA-kNN将这2个区域均预测为断层区，这表明PCA-kNN模型相较于人通过肉眼来解释响应更为灵敏，在小断层的预测方面具有一定的优势；同理，可以推测B、C两处，PCA-kNN的预测结果与人工解释结果相反，极有可能是该区域存在小断层分布，但是人工并未解释出这些断层；另外，图中的D、E处被人为地解释为断层分布区，但是PCA-kNN的预测结果显示这些区域的断层扩展长度很小，这表明这些区域断层解释的可靠性相对较低。总体来看，PCA-kNN可以实现工区的断层分布预测，并且相较于人工断层解释而言，这一方法具有快速、直观，能够更好地识别小断层的特点。

图7 kNN断层预测分布与人工解释结果对比

4 结 论

a.本文在开展研究过程中，随机形成了2种类型的数据集：其中，数据集类型1的训练数据集与测试数据集的比率为9∶1，用于表示训练数据比测试数据多的情况；数据集类型2的训练数据集与测试数据集的比率为3∶7，用于表示训练数据比测试数据少的情况。基于以上2种数据集，分析了kNN和PCA-kNN的自动断层识别的准确率，并在峰峰矿区羊东煤矿进行了基于PCA-kNN算法的断层自动识别。

b.基于kNN和PCA-kNN，数据集类型1的断层识别精度高于数据集类型2的断层识别精度。这表明断层识别的精度与数据集数量密切相关。当训练数据集的数量大于测试数据集的数量时，断层识别的准确性更高。

c. 基于数据集类型1和数据集类型2，分别开展了kNN和PCA-kNN方法的断层识别。结果表明，基于PCA-kNN模型的断层识别准确率要高于单纯基于kNN模型的断层识别准确率。特别是在数据集类型2中，当训练数据集的数量少于测试数据集的数量时，基于PCA-kNN模型的断层识别精度超过了基于kNN模型的断层识别精度。这表明由PCA形成的单个综合属性比单个地震属性具有更高的有效信息密度，并且具有进一步探查可以表征断层的地震属性的能力。

d.在实际应用中，使用所构建的模型来预测实际的断层分布。这种情况类似于本研究中的数据集类型2，即训练数据小于测试数据。为了获得比测试数据更多的训练数据，有必要在勘探区域中整合多个已知的地质数据，以进行实际的大数据分析，从而有助于形成与数据集类型1类似的情况。如果发生数据集类型2，可以考虑采用降维方法(例如PCA)来提高断层自动识别的准确性。

[1] 董守华，石亚丁，汪洋. 地震多参数BP人工神经网络自动识别小断层[J]. 中国矿业大学学报，1997，26(3)：14–18. DONG Shouhua，SHI Yading，WANG Yang. Automatic recognition of small fault by BP artificial nervous network from multiple seismic parameters[J]. China University of Mining and Technology，1997，26(3)：14–18.

[2] BAHORICH M，FARMER S L. 3-D seismic discontinuity for faults and stratigraphic features：The coherence cube[J]. AAPG Bulletin，1995，14(10)：1566.

[3] ALBINHASSAN N M，MARFURT K. Fault detection using Hough transforms[C]//Society of Exploration Geophysicists. SEG Technical Program Expanded Abstracts 2003. 2003：1719–1721.

[4] PEDERSEN S I，RANDEN T，SONNELAND L，et al. Automatic fault extraction using artificial ants[C]//Society of Exploration Geophysicists. SEG Technical Program Expanded Abstracts 2002. 2002：512–515.

[5] ADMASU F，BACK S，TOENNIES K. Autotracking of faults on 3D seismic data[J]. Geophysics，2006，71(6)：49–53.

[6] LU Cai，YUAN Mingkai，WANG Qi，et al. Application of multi-attributes fused volume rendering techniques in 3D seismic interpretation[C]//Society of Exploration Geophysicists. SEG Technical Program Expanded Abstracts 2014. 2014：1609–1613.

[7] 孙振宇，彭苏萍，邹冠贵. 基于SVM算法的地震小断层自动识别[J]. 煤炭学报，2017，42(11)：2945–2952. SUN Zhenyu ，PENG Suping ，ZOU Guangui，Automatic identification of small faults based on SVM and seismic data[J]. Journal of China Coal Society，2017，42(11)：2945–2952.

[8] DI Haibin，SHAFIQ A，WANG Zhen，et al. Improving seismic fault detection by super-attribute-based classification[J]. Interpretation，2019，7(3)：251–267.

[9] ZOU Guangui，REN Ke，SUN Zhenyu，et al. Fault interpretation using a support vector machine：A study based on 3D seismic mapping of the Zhaozhuang Coal Mine in the Qinshui Basin，China[J]. Journal of Applied Geophysics，2019，171：103870.

[10] BARNES A E. A filter to improve seismic discontinuity data for fault interpretation[J]. Geophysics，2006，71(3)：1.

[11] BAVKAR S，SAHARE S. PCA based single channel speech enhancement method for highly noisy environment[C]//2013 International Conference on Advances in Computing，Communications and Informatics(ICACCI). IEEE，2013：1103–1107.

[12] IWAI M，KOBAYASHI K. Noise reduction in magnetocardiograph based on time-shift PCA just using measurement data[C]// IEEE. 2018 IEEE International Magnetics Conference(INTER MAG). 2018：1.

[13] ARAYA M，DAHLKE T，FROGNER C，et al. Automated fault detection without seismic processing[J]. The Leading Edge，2017，36(3)：208–214.

[14] JAAFAR H，RAMLI N H，NASIR A S A. An improvement to the k-nearest neighbor classifier for ECG database[J]. IOP Conference Series：Materials Science and Engineering，2018，318：012046.

[15] AHA W，KIBLER D，ALBERT M. Instance-based learning algorithms[J]. Machine Learning，1991，6(1)：37–66.

[16] WOLD S. Principal component analysis[J]. Chemometrics & Intelligent Laboratory Systems，1987，2(1)：37–52.

[17] JOLLIFFE I T. Principal component analysis[J]. Journal of Marketing Research，2002，87(4)：513.

[18] MINCHAI H，ZHENMIN Q. Identification of the pesticide fluorescence spectroscopy based on the PCA and KNN[C]// IEEE. 2010 3rd International Conference on Advanced Computer Theory and Engineering(ICACTE). 2010，3：184–186.

[19] 周志华. 机器学习[M]. 北京：清华大学出版社，2016. ZHOU Zhihua. Machine learning[M]. Beijing：Tsinghua University Press，2016.

[20] COVER T，HART P. Nearest neighbor pattern classification[J]. IEEE Transactions on Information Theory，1967，13(1)：21–27.

[21] PETERSON L. K-nearest neighbor[J]. Scholarpedia，2009，4(2)：1883.

[22] COST S，SALZBERG S. A weighted nearest neighbor algorithm for learning with symbolic features[J]. Machine Learning，1993，10(1)：57–78.

[23] II R，FUKUNAGA K. The optimal distance measure for nearest neighbor classification[J]. IEEE Transactions on Information Theory，1981，27(5)：622–627.

[24] WRONA T，PAN I，GAWTHORPE R L，et al. Seismic facies analysis using machine learning[J]. Geophysics，2018，83(5)：83–95.

[25] ZHANG Zhongheng. Introduction to machine learning：K-nearest neighbors[J]. Annals of Translational Medicine，2016，4(11)：218.

Fault recognition based on principal component analysis and k-nearest neighbor algorithm

ZOU Guangui1,2, REN Ke2, JI Yin2, Ding Jianyu2, ZHANG Shaomin2

(1. State Key Laboratory of Coal Resource and Safety Mining, China University of Mining and Technology(Beijing), Beijing 100083, China; 2. College of Geoscience and Surveying Engineering, China University of Mining and Technology(Beijing), Beijing 100083, China)

Faults are geological structures that can cause disasters and thereby affect the safety of coal mines. Insight into the distribution of faults is one of the main purposes of 3D seismic exploration in coal mines. With respect to human-computer interaction in the interpretation of faults, the reliability of fault interpretation depends to a certain extent on the interpreter’s knowledge. We propose an algorithm based on principal components and nearest neighbors to detect the distribution of faults along target horizons. The Yangdong Coal Mine of Fengfeng Mining Area is selected as the research area, and ten seismic attributes are extracted from the data obtained via three-dimensional seismic acquisition and high-precision processing of the mining area. Principal component analysis(PCA) is used to integrate the aforementioned ten seismic attributes into six integrated attributes. At the same time, the attribute information is combined with the fault information of 139 points determined from 15 wells and 3 roadways in the mining area to construct a known data set. Based on these data, two sets of data were constructed. The ratio of training to testing data for the first and second data set was 9∶1 and 3∶7, respectively. Using these data sets and the 10-fold cross-validation method, the accuracy of fault recognition based on the k-nearest neighbors(kNN) algorithm was determined to be 87.75% for data set 1 and 71.63% for data set 2. This indicates that the accuracy of fault identification is closely related to the number of data sets. In particular, when the number of training data sets is greater than that of the testing data sets, the accuracy of fault identification is higher. The attributes obtained after dimensionality reduction via PCA were used as inputs in the evaluation of the classification results of the KNN model, and the classification accuracy rates were calculated to be 89.23% for data set 1 and 73.79% for data set 2, respectively. This is because PCA reduces the dimensionality of the original input features, thus reducing the amount of calculation required and increasing the characterization capability of these features. The results show that a combination of the PCA and kNN methods can effectively identify fault distribution, and improve the efficiency of fault interpretation.

seismic attributes; principal component analysis(PCA); k-nearest neighbor(kNN) algorithm; fault identification; Yangdong Coal Mine of Fengfeng Mining Area

P315.9

A

1001-1986(2021)04-0015-09

2020-10-14；

2020-11-11

国家重点研发计划课题(2018YFC0807803)

邹冠贵，1981年生，男，福建龙岩人，博士，副教授，博士生导师，从事地震解释、岩石物理学研究.E-mail：cumtzgg@foxmail.com

任珂，1993年生，男，山东潍坊人，博士研究生，从事地震解释研究.E-mail：renke666@foxmail.com

邹冠贵，任珂，吉寅，等. 基于主成分分析和最近邻算法的断层识别研究[J]. 煤田地质与勘探，2021，49(4)：15–23. doi: 10.3969/j.issn.1001-1986.2021.04.003

ZOU Guangui，REN Ke，JI Yin，et al. Fault recognition based on principal component analysis and k-nearest neighbor algorithm[J]. Coal Geology & Exploration，2021，49(4)：15–23. doi: 10.3969/j.issn.1001-1986.2021.04.003

(责任编辑 聂爱兰)