如何正确运用χ2检验
——高维表资料独立性检验与SAS实现
胡纯严,胡良平,2*
(1. 军事科学院研究生院,北京 100850;2. 世界中医药学会联合会临床科研统计学专业委员会,北京 100029*通信作者:胡良平,E-mail:lphu927@163.com)
对高维表资料进行独立性分析的基本思路是将高维表降为二维表,降维的重要举措就是按一个因素的全部水平或多个因素的全部水平组合对资料进行分层,从而使每层中的资料都是一个二维表资料。一种特殊的高维表就是分层后的二维表为2×2 表(即含一个二值的原因变量和一个二值的结果变量),简记为“g×2×2 表”。针对独立性检验问题,本文将介绍CMHχ2检验[1-3]和加权χ2检验[3-5]两种方法,并通过实例,介绍使用SAS 软件[1]实现计算的具体方法。
1 与高维表资料独立性检验有关的概念
1.1 高维表(g×2×2表)资料的表达模式
高维表(g×2×2表)资料的表达模式见表1。

表1 高维表(g×2×2表)资料的第h层2×2表资料的表达模式
1.2 高维表资料独立性检验的含义
设高维表资料中有K个因素(或自变量),1 个定性的结果变量。除了采用回归分析可以同时考察K个因素对定性结果变量的影响之外,差异性分析的思路是将K-1 个因素当作分层变量,只研究剩余的一个因素对二值定性结果变量的影响,这被称为将高维表降维后使其成为二维表。显然,在分层变量(它可以是1个因素,也可以是多个因素的水平组合)的每个水平下,都有一张二维表。假定分层变量有g(g≥2)个水平,则有g张2×2 表(注:本文不考虑g张R×C表)。研究者关心的是各层2×2 表资料中“原因变量”与“结果变量”之间是否独立(不独立时,就意味着存在关联),为了回答这个问题,需要进行高维表资料的独立性检验。在文献[1,3,6-7]中,实现此检验的方法叫做广义CMHχ2检验;而在文献[4-5]中叫做加权χ2检验。
2 高维表资料独立性检验及SAS实现
2.1 高维表资料加权χ2检验的具体算法
2.1.1 隐含权重的加权χ2检验的具体算法
在g×2×2 表资料中,设含有g个水平的因素为重要非试验因素,按其分层可得到g个2×2 表资料。于是,可按如下的公式将g个2×2 表资料整合成一个χ2检验统计量χ2W[3]:
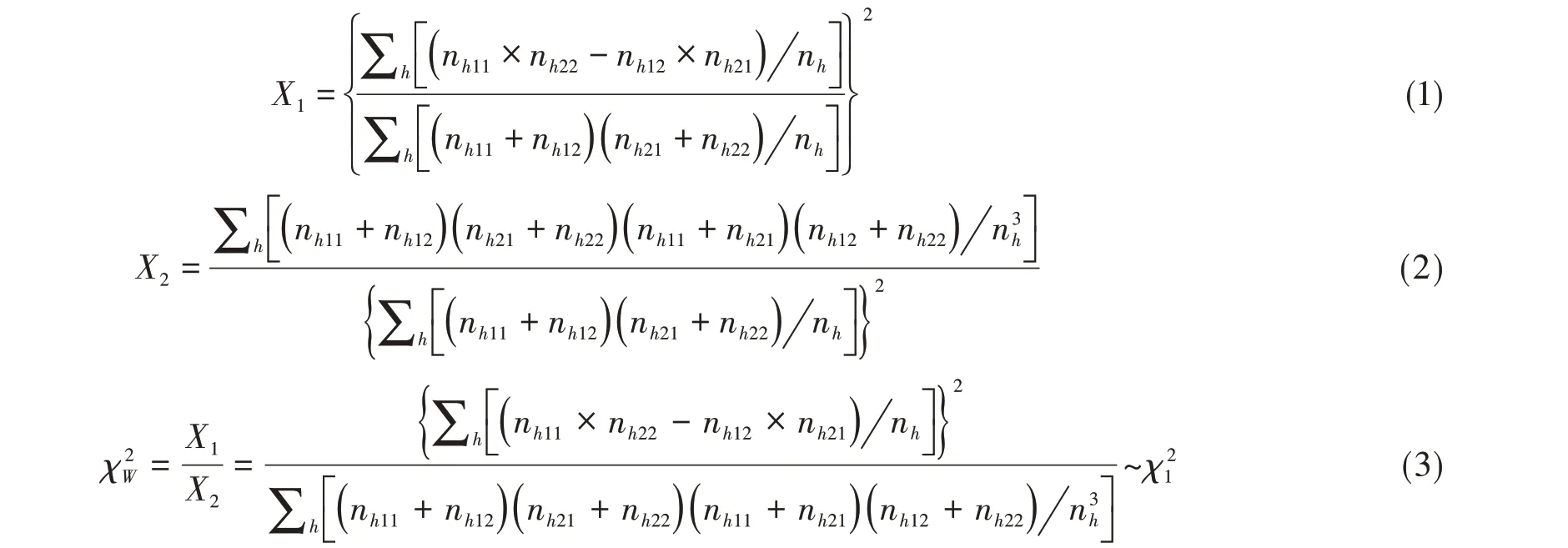
式(3)表明,χ2W服从自由度为1的χ2分布。
【说明】在式(1)、式(2)、式(3)中,看不见反映各层2×2 表资料重要性的“权重Wh”,故称式(3)为“隐含权重的加权χ2检验统计量”。
2.1.2 突显权重的加权χ2检验的具体算法
文献[4-5]提供了另一个突显权重的加权χ2检验统计量,见式(4)、式(5)、式(6):


将式(5)~式(10)代入式(4),可得到式(11):
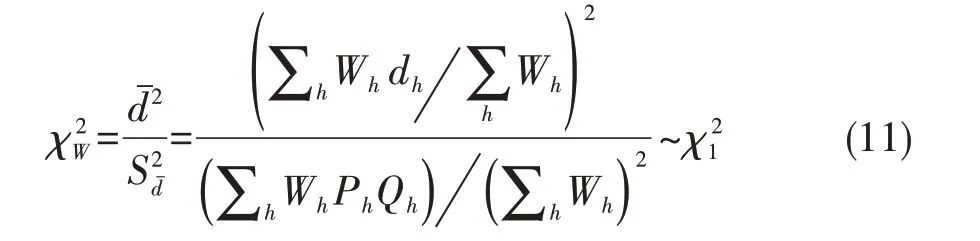
对式(11)进行变形,得到式(12):

对式(12)做进一步变形,可得到式(13):

比较式(3)与式(13)可知,它们是完全相同的。
【说明】“隐含权重的加权χ2检验统计量”实际上是在原本有“权重”的式(11)的基础上,将g×2×2 表资料中“各层原始数据以及行合计和列合计”代入公式中的有关变量并进行变形后的“结果或形式”。在本质上,只有一个“突显权重的加权χ2检验统计量”。
2.2 高维表资料CMH χ2检验的具体算法
文献[1-2]介绍了广义CMHχ2检验统计量及其三种变形。下面再介绍一种类似于加权χ2检验统计量的CMHχ2检验统计量[3],见式(14):

在式(14)中,nh11、mh11和vh11分别为第h层2×2 表资料中第(1,1)格上的“观察频数”“期望频数或理论频数”和“方差”,后两项的计算分别见式(15)、式(16):

在上面两式中,H0为该假设检验的无效假设或称为零假设,其具体表述如下。
H0:在各层2×2 表资料中,行、列两变量间互相独立。
将式(15)和式(16)代入式(14)中后再变形,得到式(17):
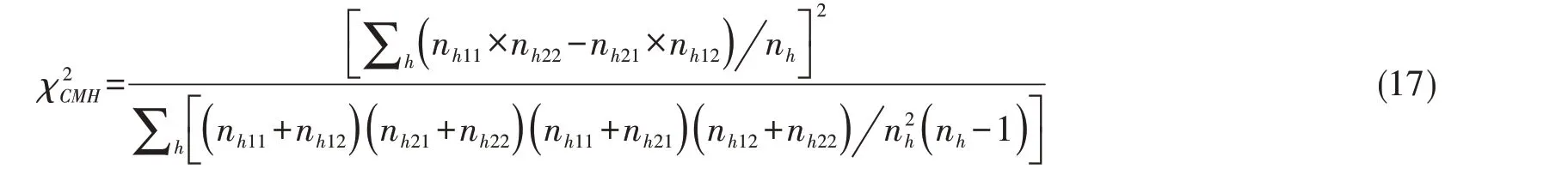

2.3 高维表资料独立性检验的SAS实现
2.3.1 问题与数据
【例1】文献[5]提供了如下资料,试分析新疗法与旧疗法的治愈率是否相等。见表2。

表2 新疗法与旧疗法对某疾病的效果
2.3.2 多项研究中两关键变量之间独立性检验的SAS实现
【例2】沿用例1 中的“问题与数据”,通常设“组别”为“分层因素”,研究者关心的是“治疗方法”与“治疗结果”之间是否存在关联性。与其等价的表述或假设是:H0:“治疗方法”与“治疗结果”之间互相独立;H1:“治疗方法”与“治疗结果”之间不独立。试基于表2 资料,检验前面给出的“检验假设”。
【分析与解答】
解法一,采用加权χ2检验。设所需要的SAS 程序如下:


【SAS输出结果及解释】
W-chisq=2.153 W-p=0.1422916183
以上输出的结果是:χ2W=2.153,P=0.142292。
【统计结论】由以上输出结果可知:χ2W=2.153,P=0.142292>0.05,说明“治疗方法”与“治疗结果”之间的关联性无统计学意义。
【专业结论】在消除年龄因素的影响之后,可以认为:新疗法与旧疗法对应的治愈率相等(说明“治疗方法”与“治疗结果”之间互相独立)。
解法二,采用CMHχ2检验。设所需要的SAS 程序如下:

【SAS输出结果及解释】

以上输出的结果是:χ2CMH=2.1334,P=0.1441。
【统计结论】由以上输出结果可知:χ2CMH=2.1334,P=0.1441>0.05,说明“治疗方法”与“治疗结果”之间的关联性无统计学意义。
【专业结论】在消除年龄因素的影响之后,可以认为:新疗法与旧疗法的治愈率相等。
3 讨论与小结
3.1 讨论
本文所介绍的统计分析方法主要适用于g×2×2表资料,而不适用于g×R×C表资料(R与C中至少有一个大于2);本法的优点是适用面较宽,即不论分层后的2×2表资料来自何种设计类型,均可使用;检验假设可笼统表述为:在分层后的各2×2表资料中,H0:“原因变量”与“结果变量”之间互相独立,H1:“原因变量”与“结果变量”之间不独立;从公式推导的最终结果可知,对于前述的“检验假设”而言,加权χ2检验统计量的数值与CMHχ2检验统计量的数值接近相等。
3.2 小结
本文针对g×2×2 表资料独立性检验问题,呈现了两种不同形式的加权χ2检验公式和CMHχ2检验公式,通过公式推导和变形,揭示出两种不同形式的加权χ2检验公式是完全相同的;同时,还揭示出加权χ2检验统计量与CMHχ2检验统计量在数值上是接近相等的。通过一个实例,展示了基于SAS 软件实现加权χ2检验和CMHχ2检验的全过程,并对SAS输出结果进行解释,做出统计结论和专业结论。

