如何正确运用χ2检验——人-时间资料独立性检验与SAS实现

胡纯严，胡良平，2*

（1. 军事科学院研究生院，北京 100850；2. 世界中医药学会联合会临床科研统计学专业委员会，北京 100029*通信作者：胡良平，E-mail：lphu927＠163.com）

人们在收集定性资料时，通常会面临如下实际问题：在所考察的处理因素分别处于“暴露”与“非暴露”水平下，观察两组受试对象是否出现某种结局时，发现各组中每位受试对象受到处理因素特定水平（“暴露”或“非暴露”）影响的时间长度可能不相同。这就意味着以各组受试对象的总人数作为计算该组样本发病率的分母是不够合理的，需要同时考虑每个人所经历的“时间长度”，它就是“人-年数”。本文介绍基于“人-年数”为“分母”的定性资料分析方法，即“人-时间资料的独立性检验”。

1 分析人-时间资料所需要的基本知识

1.1 分析人-时间资料涉及到的基本概念

1.1.1 累加发病率（简称“发病率”）

设观察由n个受试对象组成的一个群体在一个确定的时间段（例如一个月或一个季度或一年）内出现患某病的人数为m，则称该病的累加发病率（简称为“发病率”）为100（m/n）%。这里有一个隐含的假定：即所有n个受试对象都被观察了相同时间长度（例如一个月或一个季度或一年）。

1.1.2 人-年数

在现实生活和科研工作中，受试对象被观察的时间长度可能不尽相同，有些受试对象可能分别被观察了3 个月、7 个月或14 个月，如此等等。为了便于分析，不妨将“时间长度”统一折算为“一年”，称为“人-年数”。于是，分别被观察了3、7、14个月的3位受试对象，总共被观察了（3+7+14）/12=2人-年数。

1.1.3 发病密度

一组人群的发病密度（incidence density，ID）定义为：该组群中发生事件（发生疾病）的人数除以该组群在研究期间累加的人-年（时间）总数［1］。这里的分母是“人-年数”，其取值范围为0 到∞；而累加发病率的取值范围为0～1。

1.2 人-时间资料的三种常见形式

第1 种形式：未分层成组设计的人-时间资料，见表1［1］。第2 种形式：分层且含一个定性因素的人-时间资料，见表2［1］。第3 种形式：分层且含一个计量因素的人-时间资料，见表3［2］。

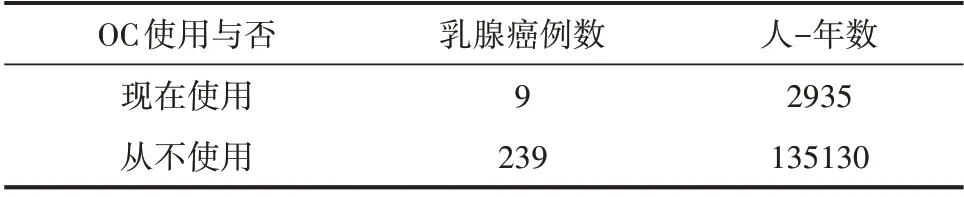
表1 某地45～49岁妇女乳腺癌发病例数与是否使用口服避孕药（OC）的关系

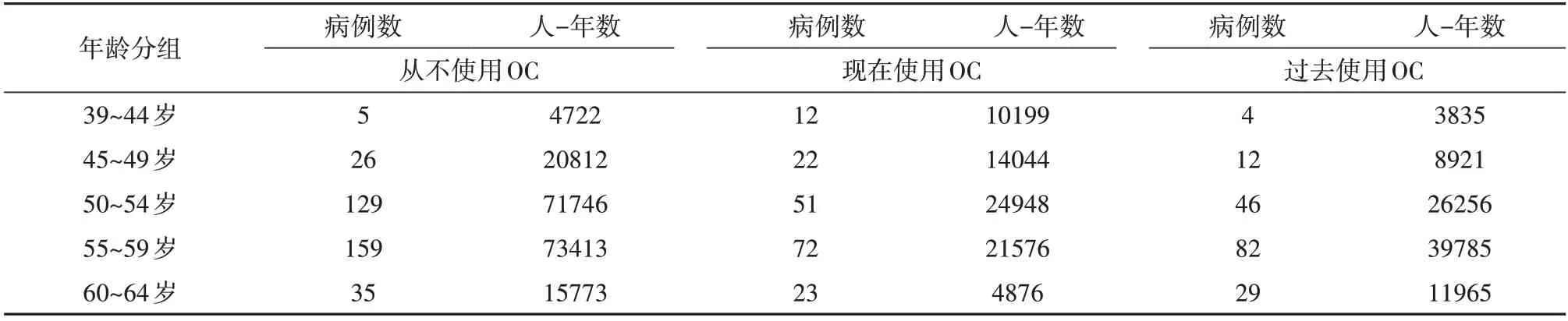
表2 绝经后期妇女是否使用OC患乳腺癌情况的调查结果

表3 某地镍精炼工人肺癌死亡情况调查结果

2 基于未分层人-时间资料比较两总体“发病密度”

2.1 未分层成组设计人-时间资料的表达模式

未分层成组设计人-时间资料的表达模式，见表4。

表4 未分层成组设计人-时间资料的表达模式

2.2 检验假设及检验统计量

检验假设可表述如下：H0：ID1=ID2；H1：ID1≠ID2；α=0.05。

根据资料所满足的前提条件，有两个可供选择的检验统计量［1-2］，分别见式（1）、式（2）：

在上面两式中，α1为表4 中“暴露水平组”的“病例数”，E1和V1分别为α1的“期望频数”和“方差”，其计算分别见式（3）、式（4）：

事实上，依据“Z2=χ21”的统计理论知识［3］，可将式（1）和式（2）合并成式（5）：

前提条件：这个检验适用于“V1≥5”。

2.3 两总体发病密度比较的SAS实现

【例1】如表1资料，试分析“现在使用OC”与“从不使用OC”两组妇女乳腺癌发病密度差异是否有统计学意义。

【分析与解答】设所需要的SAS程序［2］如下：

【程序说明】第2 句“do i=1 to 1；”代表该资料只有“一层”（相当于只有一个4 格表资料）；若整个资料有8层，此句应修改为“do i=1 to 8；”。

【SAS输出结果及解释】

以上输出结果是基于标准正态分布理论算得的，V1=5.15994 为“α1=9”的方差；而Z=1.42105、P=0.15530＞0.05。

【统计结论和专业结论】上述计算结果说明，某地45～49岁妇女使用口服避孕药与不使用口服避孕药的乳腺癌发病密度差异无统计学意义，即可以认为：口服避孕药对该地45～49 岁妇女是否患乳腺癌没有明显影响。

以上输出结果是基于χ2分布理论算得的，χ2=2.01939、P=0.15530＞0.05，结论同上，此处从略。

【说明】当自由度为1时，χ2=Z2，故当只有一个四格表资料时，前面两部分输出结果只需要保留其中任何一个即可。

3 基于分层人-时间资料比较两合并“发病密度”

3.1 资料的表达模式

为节省篇幅，资料的表达模式参见前文表2 和表4（假定其代表第“i”层）。值得注意的是：在表2中，“年龄分组”可被视为一个“分层因素”（或称为被控制的因素）；而“使用OC 的情况”可被视为该研究的一个试验因素，它有3 个水平，分别为“从不使用OC”“现在使用OC”和“过去使用OC”。

本文所介绍的方法适用于试验因素具有两个水平，对表2 资料而言，可以在分层的条件下比较“从不使用OC”与“现在使用OC”两个水平下“各层合并后的发病密度”差异是否有统计学意义；也可以比较“从不使用OC”与“过去使用OC”两个水平下“各层合并后的发病密度”差异是否有统计学意义。

3.2 检验假设及检验统计量

检验假设可表述如下：H0：合并ID1=合并ID2；H1：合并ID1≠合并ID2；α=0.05。

检验统计量［1-2］见式（5）：

前提条件：①假定各层发病密度之比［RRi=（α1i/t1i）/（α2i/t2i），i=1，2，…，k］相等；②Var（A）≥5。

3.3 两总体合并发病密度比较的SAS实现

【例2】如表2 资料，试分析按年龄分组且在“从不使用OC”与“现在使用OC”两个条件下，合并的妇女乳腺癌发病密度差异是否有统计学意义。

【分析与解答】设所需要的SAS程序［2］如下：

后面紧接其他SAS 程序语句，具体内容与“第2.3 节”中自“data a；”到最后完全相同，为节省篇幅，此处从略。

【SAS输出结果及解释】

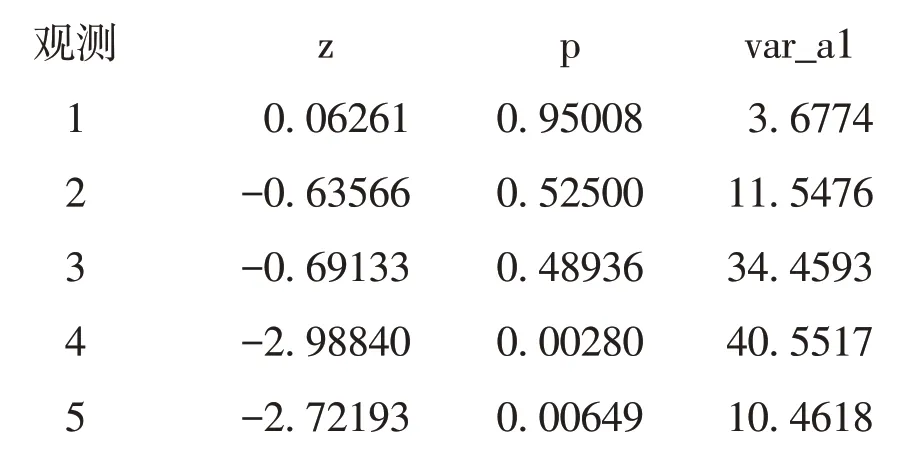
以上输出的是表2 中5 个“年龄分组（层）”各自的计算结果，其中，Z、P和Var_a1 分别代表“检验统计量”“P值”和“各层α1的方差”。由“P值”列可知，只有在最后两个年龄组中，“从不使用OC”与“现在使用OC”两个条件下，妇女乳腺癌发病密度差异有统计学意义。

以上输出的是表2 中5 个“年龄分组（层）”合并后的计算结果，即χ2=12.8219，P=0.000343＜0.01。

【统计结论和专业结论】上述计算结果说明，在“从不使用OC”与“现在使用OC”两个条件下，合并后的妇女乳腺癌发病密度差异有统计学意义。从表2 中的实际数据可知，“现在使用OC”者的乳腺癌发病密度比“从不使用OC”者的乳腺癌发病密度大。

4 讨论与小结

4.1 讨论

采用“人-年数”取代“总样本含量”是人们在处理定性资料时，严格遵照“实事求是”原则的一个具体体现，是统计学的一个微小进步。然而，在实际科研工作中，精准地获得各组受试对象的“人-年数”是十分困难的事，尤其是在观察时期较长、回顾性研究且各组样本含量较大的情境中。因此，应尽可能事先制订出相对完善的研究设计方案，并严格执行研究设计方案（包括“标准操作规程方案”和“实时精准质量控制方案”等）［4-5］，以确保所获得的科研数据是精准可靠的［6-7］。

4.2 小结

本文介绍了与“人-时间资料”有关的基本知识、基于未分层人-时间资料比较两总体“发病密度”和基于分层人-时间资料比较两合并“发病密度”等内容；通过两个实例，介绍了基于SAS软件实现前述两种场合下的统计计算方法，对SAS 输出结果进行解释，并做出了统计结论和专业结论。