延性金属层裂自由面速度曲线特征多尺度模拟研究*
王云天,曾祥国,陈华燕,杨 鑫,王 放,祁忠鹏
(1.四川大学建筑与环境学院,深地科学与工程教育部重点实验室,四川 成都610065;2.成都理工大学环境与土木工程学院,地质灾害防治与地质环境保护国家重点实验室 四川 成都610059;3.西南大学材料与能源学院,重庆400715)
延性金属在强动载荷下的动态破坏是冲击动力学中重要的基础科学问题之一,随着国防建设、汽车工业以及航空航天等领域的发展,深入地了解延性金属在高速冲击下的动态损伤有着重要的意义[1]。层裂是延性金属动态损伤的一种典型表现形式,层裂实验中得到的自由面速度曲线包含了延性金属在动态破坏过程中的丰富信息[2-3]。在对延性金属层裂行为的研究中,平板撞击(planar plateimpact,PPI)实验是目前主要采用的一种研究方法,实验过程中内部波系传播如图1(a)所示:飞片在t0时刻以一定速度撞击样片,二者相撞时会分别传入冲击波,当冲击波到达样片自由面和飞片后表面后会形成反射稀疏波,两束稀疏波会在样片内部相遇并产生拉伸区域,由此引起的内部损伤逐渐累积,直至材料失效断裂。Curran 等[3]基于对大量实验结果的分析,指出延性金属的层裂是由于内部的微损伤形核、生长和聚集后,形成层裂飞片的复杂动力学过程。
Antoun 等[4]对层裂的研究历史和现状作了权威性总结,指出了层裂研究还有许多问题尚待解决。Thomas等[5]采用对称碰撞的方式研究了铁在低于冲击相变阈值下的层裂行为,并对铁在低速冲击下的Hugoniot 弹性极限与层裂强度进行了分析;陈永涛等[6]采用等厚对称碰撞实验,研究了纯铁在冲击压力超过相变阈值时的层裂行为,发现样品中出现了二次层裂现象;翟少栋等[7]通过轻气炮加载与激光加载两种方式研究了铝的层裂特性,结果表明铝的层裂强度具有明显的应变率效应;Koller 等[8]通过改变冲击波波形,对无氧铜在不同冲击波形式下的层裂特性进行了研究,结果表明冲击波波形与拉伸脉冲的持续时间会显著影响无氧铜样片中的层裂损伤演化。实验研究在宏观尺度上提供了大量宝贵的实验数据,但由于其自身的特点,难以直接测量延性金属内部物理量随时间的变化数据,只能通过如自由面速度曲线等间接数据分析材料内部损伤演化过程。
随着计算机的发展与应用,数值模拟方法已经成为实验研究的有力补充。目前在冲击力学的数值模拟研究中主要有两种方法,网格法与无网格法,其中无网格法以光滑粒子流体动力学法(smootfied particle hydrodynamics SPH)[9]为代表得到了广泛应用。张凤国等[10]对延性金属在三角波加载下多次层裂破坏问题进行了数值模拟研究,对比分析了应力瞬时断裂准则和Tuler-Butcher 准则的差异,结果表明影响层裂片厚度的主要因素是材料自身的物理性质和加载条件;种涛等[11]基于一维流体动力学数值模拟方法,分析了铁层裂损伤与冲击相变之间的相互影响;Glam 等[12]采用数值模拟方法研究了温度效应对铝的层裂强度与Hugonoit 弹性极限的影响,结果表明铝的初始温度与层裂强度正相关。Libersky 等[13]率先在SPH 方法中引入了材料强度效应;徐金宏等[14]利用一种改进SPH 方法对靶板厚度、弹丸速度和形状对碎片云的影响进行了研究;Zhou 等[15]在对铝球超高速撞击靶板的研究中,利用SPH 方法成功地进行了数值模拟分析,结果与实验数据有较好的吻合性。贺年丰等[16]采用SPH 方法对爆轰条件下锡的层裂行为进行了数值模拟,结果表明SPH方法得到的结果与实验数据有很好的一致性;可以看出,在宏观尺度上,数值模拟方法与实验有很好的吻合性,并且数值模拟的加载范围与条件更加灵活,计算快速、结果直观,可以获得材料宏观尺度上的动态破坏信息,但数值模拟结果的准确定取决于采用的受状态方程、强度模型和失效模型等因素,并且由于单元或粒子尺度影响,从微观尺度研究层裂机理的能力有限。
在微观尺度,分子动力学方法(molecular dynamics,MD)已经逐渐成为一种在微观尺度研究材料性能的主流方法。席涛等[17]通过分子动力学方法研究分析了超高应变率下铜的层裂特性,获得了铜在109~1010s−1时的层裂强度;Rawat 等[18]研究了应变率对单晶铁中的损伤演化的影响,结果表明随着应变率的增加,空洞更容易成核,但在低应变率条件下空洞的生长速度更快;Yang 等[19]研究了应变率、温度、晶粒尺寸等因素对铝动态损伤发展的影响,揭示了不同影响因素下损伤发展的过程;Chen 等[20]通过分子动力学方法研究了晶界特性对动态损伤的影响,结果表明损伤分布与晶界取向和空洞形核应力相关。可以看出:分子动力学模拟可以揭示动态损伤的微观机理,给出材料内部应力与损伤演化信息,有助于从根本上了解金属材料的动态损伤机制,但受到计算能力的限制,无法在全尺寸上复现层裂现象[21-23]。
典型自由面速度曲线如图1(b)所示,从中可以分析得到延性金属材料动态损伤的宏观响应的一系列重要信息,如加载应力幅值、拉伸应变率、层裂强度和层裂片厚度等,因此自由面速度曲线是研究层裂演化过程的最重要参考数据之一[24]。实际上延性金属的层裂过程十分复杂,是一种内部损伤随时空演化的动力学过程,材料从受到拉伸应力影响开始直至完全破坏要经历一个损伤累积的过程,期间会伴随能量的耗散和性能的退化,这都会影响材料内部波的传播过程,从而影响自由面速度曲线的形式。因此,自由面速度曲线是微观上的损伤演化过程和宏观响应场之间相互作用的一种宏观表象,由于宏观尺度上的实验和数值模拟很难得到反应内部损伤演化的信息,这对充分认识宏观响应与微观损伤发展之间的关系造成了阻碍,也就导致对自由面速度曲线中的一些特征理解存在争议。裴晓阳等[2]基于理论分析和微观损伤演化动力学理论,对延性金属层裂自由面速度曲线的某些特征所对应的物理内涵进行了阐述,定性地指出了宏观上自由面速度曲线的响应特征与内部损伤演化的对应关系,但是并没有从微观尺度上的给出材料层裂过程中的损伤演化过程,缺少在微观尺度的机理分析与验证。
目前的研究大多只局限于单一尺度下层裂现象模拟或微观损伤演化分析,少有结合宏观与微观尺度下对层裂自由面速度曲线特征的多尺度视角下的研究,缺乏对自由面速度曲线的微观视角解析。本文以延性金属钽为研究对象,在宏观尺度上对钽在高速冲击下的层裂行为进行数值模拟,通过与实验数据的比较,验证模型的合理性;在微观制度上通过分子动力学方法分析钽在层裂过程中的损伤演化过程。进而将宏观尺度与微观尺度的模拟结果有机结合起来,从多尺度视角对延性金属钽的层裂行进行研究。揭示了自由面速度曲线上的典型特征所蕴含的损伤演化规律和及物理内涵,研究结果可以为全面了解层裂这一复杂的动力学行为提供参考。
1 计算模型与方法
为了便于与实验数据进行对比验证,宏观尺度全尺寸模型参照平板撞击实验建立[25],选取样片自由面中心位置数据绘制自由面速度曲线,如图2(a)所示;微观尺度分子动力学模型选取样片中心拉伸区域进行模拟,MD模型如图2(b)所示。
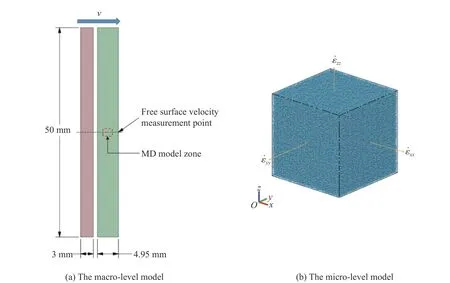
图2 多尺度模拟模型示意图Fig.2 Configurations of the multi-scale simulation models
1.1 宏观尺度数值模拟
1.1.1状态方程与材料本构
Mie-Grüneisen 状态方程能够较为准确地描述金属在冲击载荷下的动力学行为,其表达式如下[16]:

式中:ρ为冲击后材料密度,ρ0为初始材料密度,S1为材料常数,γ 为Grüneisen 系数,e为质量内能。Mie-Grüneisen 状态方程参数如表1所示[26]。

表1 Mie-Grüneisen 状态方程参数Table 1 Parameters for Mie-Grüneisen equation of state
考虑了三种常用的描述延性金属在强动载荷下的动态破坏行为的模型,分别是Johnson-Cook(JC)模型[27]、Steinberg-Cochran-Guinan(SCG)模型[28]以及Zerilli-Armstrong(ZA)模型[29]。
(1)JC模型
JC模型假设材料各向同性,综合考虑了应变、应变率硬化和温升软化等因素,并且将应变、应变率硬化效应和温升软化效应解耦,JC模型的表达式为:

式中:A、B、C、n、m为材料常数,Tr为参考温度,Tm为材料融化温度,ε˙0为参考应变率。JC模型参数如表2所示[30]。

表2 Johnson-Cook 模型参数Table2 Parameters for the Johnson-Cook model
(2)ZA 模型
基于热激活和位错动力学理论,Zerilli等[29]提出了一种描述体心立方金属(BCC)的强度模型,考虑了温度、应变率与温度的影响,ZA 模型的表达式为:
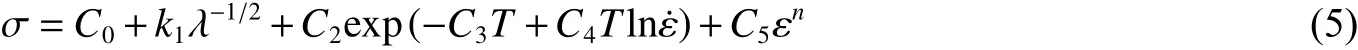
式中:C0、k1、C2、C3、C4、C5为材料常数,T为绝对温度,ε 为塑性应变,λ 为晶粒尺寸。ZA 模型参数如表3所示[29]。

表3 Zerilli-Armstrong 模型参数Table 3 Parameters for the Zerilli-Armstrong model
(3)SCG 模型
Steinberg 等[28]提出的SCG 模型考虑了静水压力对剪切模量和屈服强度的强化效应以及温度软化效应,同时忽略了应变率效应,并假设金属在融化状态下可以忽略材料强度。屈服强度Y和剪切模量G分别为:

式中:Ymax为最大屈服强度。SCG 模型参数如表4所示[28]。

表4 Steinberg-Cochran-Guinan 模型参数Table 4 Parameters for the Steinberg-Cochran-Guinan model
1.1.2层裂模型
Grady[31]基于断裂力学理论提出了层裂的能量平衡破碎模型,将层裂强度ps与层裂碎片平均尺寸和应变率联系起来。对于延性金属,层裂强度随冲击加载过程而改变,表达式为[32]:

式中:ρ为材料密度,Y为屈服强度,c0为材料体积声速,εc为材料临界失效应变,对金属材料一般可取为0.15[31]。
1.2 自由面速度曲线分析
层裂强度是表征材料在强动载荷下性能的一个重要指标,在材料动态损伤研究中具有重要参考意义。Novikov[33]基于声学近似的方法给出了计算层裂强度的公式:

式中:ρ0为材料初始密度,cb为材料初始体声速,Δus为自由面速度曲线最大值与第一次速度拉回时的差值。
层裂区域平均拉伸应变率ε˙s的计算公式为[34]:

式中:Δus与Δts分别为自由面上速度最大值和第一个极小值之间的速度差和时间差。
自由面速度回跳速率,即极小值到峰值速度之间的斜率,计算公式为:

式中:Δur与Δtr分别为自由面上速度第一个极小值与其后峰值之间的速度差和时间差。
层裂片厚度h为:

式中:Δt为第一个层裂振荡周期持续时间,cl为弹性纵波声速。
1.3 微观尺度MD模型
钽原子间的相互作用采用Ravelo等[35]提出的嵌入原子势函数,MD模拟基于Lammps 软件[36]进行。MD模型尺寸为16.53 nm×16.53 nm×16.53 nm,共250000个原子,在模型x、y、z方向施加周期性边界条件。加载之前采用NPT 系综对模型进行30 ps的弛豫,确保体系在施加荷载之前处于平衡状态;加载过程采用NVE 系综,在x、y、z方向施加相等的应变率,为了保持与宏观尺度模拟的一致性,施加应变率数值与宏观尺度模型中的拉伸应变率相同。
2 宏观尺度模型验证
分别采用Lagrange网格法与SPH无网格法结合三种强度模型对钽的层裂进行了模拟,并对二者得到的结果进行了比较分析。表5中列出了用于验证的模型尺寸参数、撞击速度、强度模型等信息。模型为二维轴对称,Lagrange 网格尺寸为0.05 mm,SPH 粒子尺寸为0.1 mm,样片直径为50 mm,撞击速度为306 m/s。

表5 用于验证的模型编号及参数设置Table 5 Model number and parameter settings for validation
不同模型得到的自由面速度曲线如图3所示。从模拟结果与实验数据对比可以发现,Lagrange 网格法与SPH 无网格法在数值模拟中各有优势,在0~2µs时,样片自由面速度曲线速度由0 m/s增加到最大值,Lagrange方法得到的模拟结果与实验数据有较好的吻合性,并且Lagrange 方法得到的结果可以观察到明显的Hugoniot 弹性极限信号,而由SPH 方法得到的结果Hugoniot 弹性极限信号不是特别明显;在自由面速度开始下降后,Lagrange方法得到的模拟结果中自由面速度回拉速率比实验数据更快,SPH方法得到的结果与实验数据较为吻合。结果表明采用SPH 无网格法在钽层裂模拟中是可行的,结合两种方法可以得到完整的自由面速度曲线数据。此外,结果表明SCG 模型在钽的层裂模拟中更为适合。
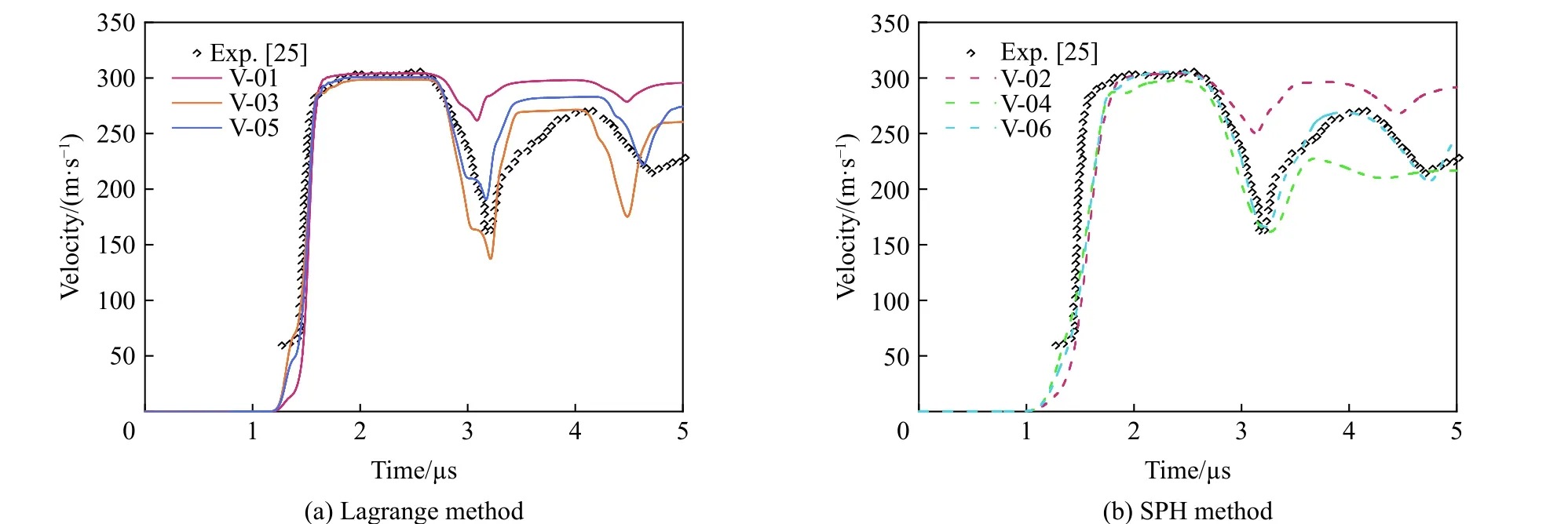
图3 不同模型的自由面速度曲线与实验数据[25]对比Fig.3 Comparison of free-surface velocity profiles by different models with experiment data[25]
为了分析不同加载应变率下的层裂特性,通过改变加载条件改变了层裂区域的拉伸应变率,表6给出了模型加载条件参数,拉伸应变率范围为2.13×104~5.40×104s−1,压力范围为6.19~12.25 GPa。不同拉伸应变率下的钽层裂宏观尺度数值模拟结果如图4所示,从图中可以看出,自由面最大速度与飞片撞击速度基本相同;在相同的加载速度下,通过改变飞片厚度自由面速度平台宽度也随之改变,二者之间呈现正比关系,飞片厚度越大,自由面速度曲线平台宽度越宽。

表6 不同应变率下平面撞击层裂模型参数与结果Table 6 Parametersof planar plateimpact simulationsand resultsunder various strain rates

图4 宏观尺度下不同拉伸应变率自由面速度曲线Fig.4 Free surface velocity under various tensile strain rates at macro-scale
3 结果分析
3.1 层裂强度
层裂强度是金属材料动态损伤行为的重要参数之一,通过对模拟结果的分析同时参照文献[3]给出的铜层裂强度与拉伸应变率的关系σspall=0.15ε˙0.2,我们得到了钽的层裂强度与拉伸应变率之间的关系:

图5给出了钽的层裂强度与拉伸应变率的关系,从图中可以发现,层裂强度不是一个仅受到加载速度影响的物理量,在加载速度相同的条件下,S-06、S-04、S-01的层裂强度随着拉伸应变率的升高而增加,对于S-05、S-03、S-02尽管加载速度相差较大,但是同样表现出层裂强度与拉伸应变率之间的正比关系。这表明层裂强度呈现出一种率相关特性,即随拉伸应变率的增长而增加。
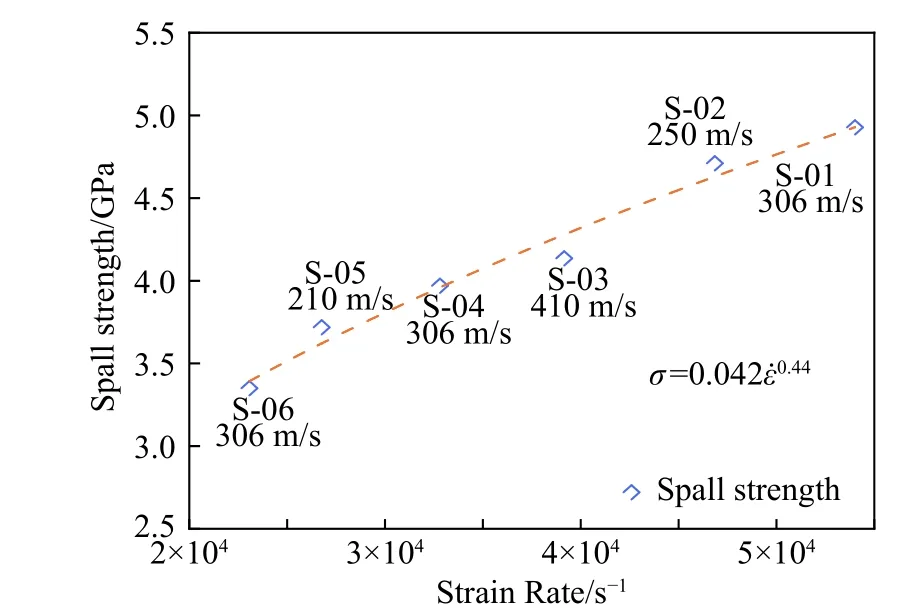
图5 层裂强度与拉伸应变率关系Fig.5 Relationship between spall strength and tensile strain rate
图6给出了对数坐标下σspall与ε˙s之间的关系,从图中可以看出在对数坐标下层裂强度表现出了明显的率相关特性。我们对比了更高拉伸应变率下的实验数据[37],更高的拉伸应变率下层裂强度同样是随应变率提高而增加,同时这也验证了数值模拟结果的准确性。

图6 对数坐标下层裂强度与拉伸应变率的关系Fig.6 Relationship between spall strength and tensilestrain rate in logarithmic coordinates
前文分析中的层裂强度是根据式(11)进行计算得到的,也是目前研究中广泛采用的声学近似计算方法,但并不是唯一的计算方法。Stepanov[33]指出,对于延性金属,平板撞击过程中冲击应以弹性纵波速度cl传播。而在它前面的入射稀疏塑性波应以体积声速cb传播,当重点考虑弹性波的影响时,有效声速ce为:

据此,可得到层裂强度的一种修正形式:

式中:ρ0为材料密度,∆u为自由面上速度最大值和第一个极小值之间的速度差。除此之外,Kanel[38]指出在层裂强度计算中还应考虑层裂片厚度影响,当计及层裂片厚度影响时:

式中:u˙1为样品自由面速度-时间曲线上Pullback 信号出现前的速度变化率,u˙2为层裂反弹信号的速度变化率,hsp为层裂片厚度。由3种公式计算得到的层裂强度如表7所示,分析发现式(17)与式(11)得到的结果最大相差8%,式(18)与式(17)得到的结果相差不大。表明通过自由面速度曲线来计算层裂强度与选用的计算方法相关,而且不同计算模型之间存在一定差异,在分析时应该得到关注。

表7 不同计算公式得到的层裂强度Table7 Spall strengths obtained by different formulas
3.2 自由面速度曲线特征多尺度分析
从宏观尺度下层裂特性的分析可以看出,自由面速度曲线反映了层裂过程中材料内部损伤演化与宏观响应场的相互作用,全面和准确地认识自由面速度曲线对研究层裂现象具有重要的意义。基于目前的研究手段,对层裂过程中损伤演化的原位观测依然难以实现,无法直观的准确的了解层裂过程中材料的宏观动力学响应与微结构演化之间的关系,进而导致对自由面速度曲线的理解也存在一些争议,例如:Pullback 信号的意义、损伤演化的形式、回跳速率的意义等。针对以上几个方面的问题,通过分子动力学方法给出层裂过程中损伤演化的情况,定性的从微观尺度对自由面速度曲线上的一些典型特征进行解读。
3.2.1 Pullback 信号
Pullback 信号是用来判断层裂是否发生的重要依据,但此时材料是否完全分离尚存争议。Zurek 等[39]认为Pullback 信号出现时材料已经完全分离,但Kanel等[40]等观察到在层裂面损伤很小时,依然有Pullback 信号出现;Bonora 等[2]认为Pullback 信号的出现与微孔洞成核相关,但未给出验证。下文以S-04加载情况为例,对其自由面速度曲线中Pullback 信号意义从微观尺度进行了分析。
图7~8给出了自由面速度下降后的时程曲线与层裂区MD模型内部应力及损伤演化情况,在分析中考虑了自由面速度曲线中Pullback 信号在选取时的误差,将Pullback 信号出现时间扩展为0.05µs时间范围进行分析。从图7中可以看出,在Pullback 出现的时间范围内,层裂区域内的应力达到峰值,在经过Pullback 信号后,层裂区域内的应力迅速下降,出现应力松弛;对比此时层裂区域内的损伤发展可以发现,Pullback 信号出现的时间范围对应的是损伤发展的初始阶段,也就是微孔洞成核阶段。在图8中可以直观的观察到内部损伤演化的情况,可以看出,在Pullback 信号时间内微孔洞开始逐渐产生,此时内部孔洞体积占比非常小,这都表明钽在Pullback 信号出现的时间范围内层裂区域实际上并未完全分离,而且Pullback 信号对应的实际上是内部微孔洞形核的过程,从微观尺度证明了Bonora 等[2]的推测。此外,在通过自由面速度曲线计算层裂强度时,Pullback 对应的速度降低幅值(图1b中Δu)是一个重要的依据,通过前面的分析表明在钽的层裂中自由面速度曲线Pullback 信号对应的是微孔洞形核的过程,这表明Δu实际上反映了了微孔洞形核的条件,那么通过Δu得到的层裂强度更准确地说应该是抵抗损伤起源的强度或微孔洞成核的一种表征。

图7 Pullback 信号及其对应的MD模型应力与空洞演化情况Fig.7 Pullback signal and the stress and void volume evolution in the MD model
层裂区域的损伤演化在宏观尺度的试验下难以直接观测,借助微观尺度的MD模型,可以从微观尺度对钽层裂过程中的损伤演化进程进行分析。在图9~11中我们给出了损伤演化过程中内部孔洞所占体积分数、微孔洞数量与内部孔洞情况。从图9中可以看出层裂区域内微损伤的演化可以分为3 个阶段:孔洞形核(S1)、长大(S2)与聚集(S3)。在内部压力达到峰值附近时,微孔洞开始形核,此时孔洞数量快速增加,但是孔洞体积占比非常小,在S1阶段空洞数量演化情况如图10所示;随后进入孔洞长大阶段,此时应力开始快速下降,而应力松弛意味着出现能量耗散,耗散的能量为孔洞长大提供动力,孔洞的快速增长导致孔洞占比迅速升高,孔洞数量在这个阶段开始降低,这表明在S2阶段中孔洞体积的增加是由于孔洞长大所致,而不是新孔洞出现造成的;在应力下降到稳定状态后,孔洞开始进入聚集阶段,此时孔洞体积占比增长速度降低,并且孔洞数量趋于稳定,这表明在损伤发展后期是层裂区域内大孔洞再聚集最终导致层裂的过程,S2阶段的空洞长大与S3阶段的空洞聚集过程如图11所示。
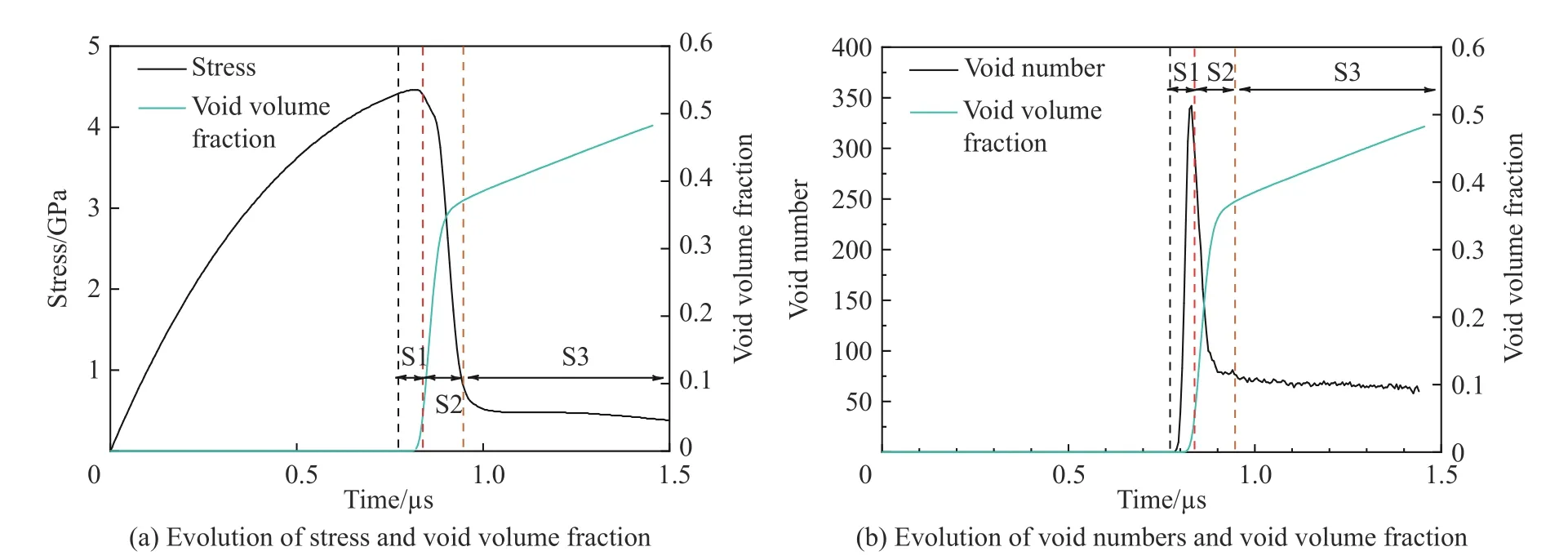
图9 空洞体积演化与应力及空洞数量的关系Fig.9 Relationship of the evolution of void volume with stress and void numbers

图10 阶段1的空洞数量演化情况Fig.10 Void number evolution during stage 1

图11 阶段2与3的空洞长大与聚集情况Fig.11 Void growing and coalescence during stage2 and stage 3
3.2.2回跳速率
在以往的分析中,往往只是关注Pullback 信号及其前段自由面速度曲线,对Pullback 信号出现后的自由面速度回跳曲线少有涉及。以自由面速度曲线中Pullback 信号为起点,分析了自由面速度回跳曲线的变化情况,不同应变率条件下的自由面速度回跳曲线如图12所示。从图中可以看出,自由面速度回跳曲线随加载速度和飞片厚度没有明显的变化趋势,但是随着拉伸应变率的增加,曲线逐渐变得陡峭,斜率逐渐增加。

图12 自由面速度回跳曲线Fig.12 Free surface velocity curve from spall signal
图13给出了层裂强度与回跳速率之间的关系。可以看出,层裂强度与回跳速率之间近似呈线性增长的关系,而层裂强度具有率相关特性,这表明自由面速度回跳曲线也与应变率相关。

图13 层裂强度与回跳速率的关系Fig.13 Relationship between spalling strength and rebound rate
自由面速度回跳与拉伸应变率的关系如图14所示。从图14中可以看出,自由面速度回跳速率随着拉伸应变率的升高而增长,二者近似呈线性变化趋势。因此,可以推断钽在层裂过程中样片内部的损伤演化速率也是随拉伸应变率的增长而增加。
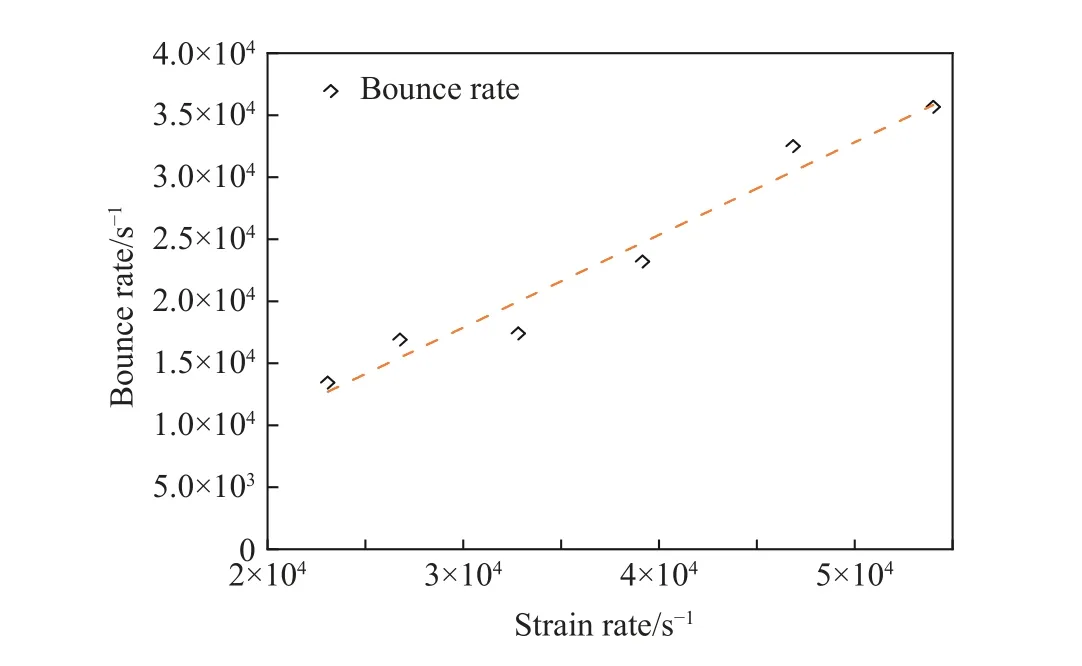
图14 不同拉伸应变率下自由面速度回跳速率Fig.14 Free surface bounce rate under various tensile strain rates
从图9中发现Pullback 信号后自由面速度回跳时间段内层裂区域内损伤快速增长的阶段,微孔洞体积占比迅速增加,这表明自由面速度回跳与损伤演化之间存在对应关系。Kanel 等[40]基于特征线方法分析了回跳速率和损伤演化速率的关系,指出二者之间是正比关系。图15给出了层裂区域内不同应变率下应力演化的情况,不同应变率下损伤演化的情况如图16所示。

图15 不同应变率下应力时程曲线Fig.15 Histories of stress under different strain rates
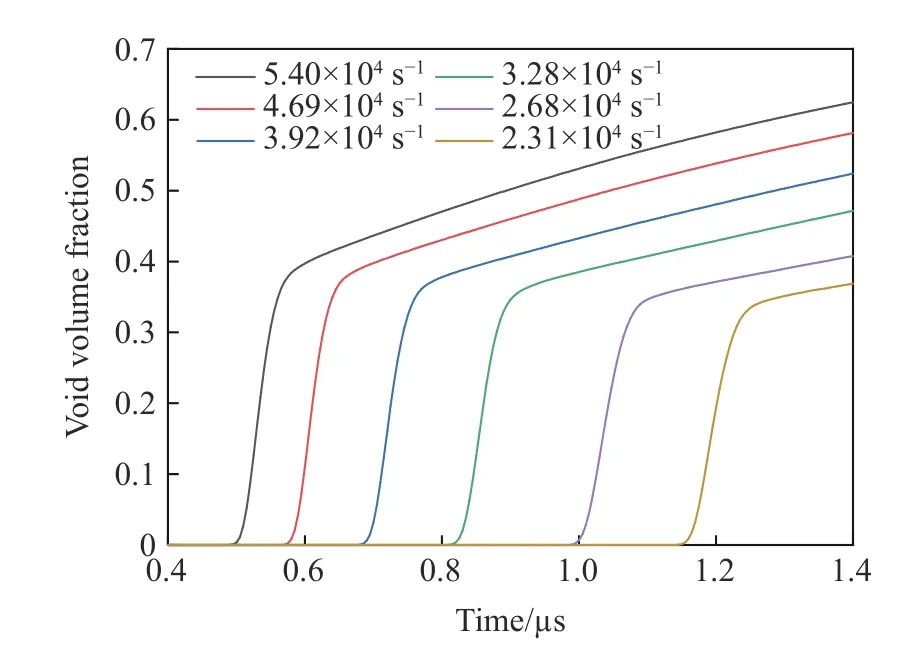
图16 不同应变率下损伤演化情况Fig.16 Damage evolution under different strain rates
从前文的分析中,我们发现回跳速率与拉伸应变率二者近似呈线性变化趋势,拉伸应变率越高,回跳速率越大。不同应变率下应力演化情况如图15所示,从宏观上波系分析可知自由面速度回跳速率与应力松弛速度相关,从层裂区域中的应力变化情况可以发现,应力下降速度随应变率的升高而加快,这表明回跳速率与应力松弛速度是呈正相关的。应力松弛速度越快,代表能量耗散的速度越快,而能量耗散的速度与损伤演化的速度相关。图16给出了不同应变率下损伤演化的情况,可以明显看出随着应变率的增加,微孔洞在长大阶段的速度越来越快。综上所述,自由面速度回跳速率是层裂区域损伤演化速率的宏观表征。
4 结 论
本文以延性金属钽为研究对象,通过改变飞片厚度与加载速度改变加载应变率,对不同加载条件下的自由面速度曲线特性进行了分析。重要的是,结合宏观和微观尺度视角揭示了自由面速度曲线与微损伤演化之间的联系,特别是对自由面速度曲线上的一些典型特征的物理内涵从微观尺度进行了解读,结果表明:
(1)对钽层裂的宏观尺度模拟中,Lagrange方法在模拟钽的弹塑性转变过程有较好的表现,能够观测到明显的Hugoniot 弹性极限信号,SPH 方法得到的结果与实验数据更为符合,能够较为准确地描述层裂全过程中的自由面速度曲线变化情况,证明SPH 方法研究钽的层裂行为是可行的;
(2)在宏观尺度上,钽的层裂强度随加载应变率的升高而增加,二者近似呈指数关系;分析表明,层裂强度与回跳速率之间存在正比关系,表明自由面速度回跳速率也是层裂行为的一种反映,应该得到关注;通过观察发现了回跳速率与拉伸应变率之间近似为线性关系,随拉伸应变率的升高而增长。
(3)微观尺度分析表明,自由面速度曲线是层裂区域内的微孔洞形核、长大、聚集直至完全断裂的微损伤演化过程的宏观反映。Pullback 信号的临界点是微孔洞的形核在宏观上的表征,自由面速度曲线在Pullback 信号前的下降幅值代表了微孔洞形核的条件,而由此计算得到的层裂强度反映了微孔洞形核强度,Pullback 信号后速度回跳速率反映了层裂区域内损伤演化的速率。

