基于传力路径分析的结构承载性能评价与优化*

王朝华 吴凤和② 郭保苏②

(①燕山大学，河北 秦皇岛 066004；②河北省重型智能制造装备工程技术研究中心, 河北 秦皇岛066004)

承载结构的高刚度、高强度、低重量设计是结构工程师长期追求的目标，特别是航天、航空及汽车等领域[1]，结构承载性能的评价与优化成为轻量化设计过程中的一个关键问题。结构优化方法因能在概念设计阶段提供轻质、高效的结构形式，在详细设计阶段提供最佳尺寸参数，受到各行业学者的广泛关注[2-3]，包括拓扑优化、形状优化和尺寸优化，通过建立严密的数学模型，多次迭代搜索得到优化方案，其优化的本质属于黑箱模型优化，是基于数值分析不断迭代搜索得到的结果，无法给出优化结果的原因及力学解释[4]。

传力路径[5]是指力在结构中的传递路线，始于力的作用点，到对应的平衡反力处终止，其作为1种新的设计理念，近年来受到学者们的广泛关注，文献[6]认为力总是沿着结构刚度最大的通道传递，提出了一种基于相对刚度的传力路径可视化法，在汽车等结构的传力性能评价中得到应用[7]，但该方法目前的评价准则主要依赖于理想结构的传力路径与实际传力路径的差值分析，而不同结构的形状轮廓往往与理想传力路径存在较大区别，另外，该方法未给出详细的承载性能优化思路，其适用性有待提升。

本文给出传力路径计算基本思路，提出结构承载性能评价及优化方法，进一步提出将材料沿传力路径布置以最大限度发挥结构承载性能的设计思路，实现承载结构的高刚度设计。

1 传力路径可视化

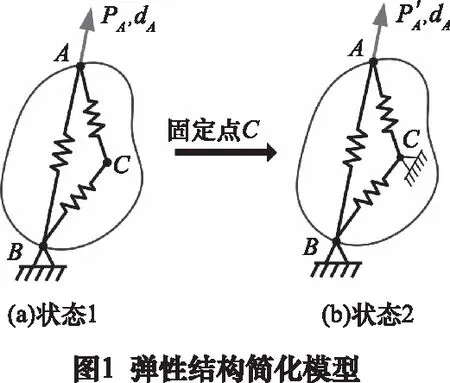
对于任意弹性结构，都可以将其简化为图1a所示模型，包括受力点A、支撑点B和任意点C，三点之间可近似为弹簧连接，用来表示任意两点之间的相对刚度。

根据相对刚度[8]的定义，3点间的力-位移关系如式(1)所示。

(1)

式中：Kij(i,j=A,B,C)表示相对刚度矩阵，pi(i=A,B,C)和di(i=A,B,C)表示载荷向量和位移向量。

其次，在点A处施加力PA，产生位移dA，根据式(1)及应变能公式，计算总应变能U为

(2)

然后，将结构中任意点C固定，如图1b所示，在点A处施加力PA，使受力点A产生相同的位移dA，此时结构的应变能U′为：

(3)

引入应变能系数U*，计算公式为

(4)

可知，U*是KAC的函数表达式，其物理意义是指受力点A和任意点C之间的刚度关系。最后，将具有相同U*值的节点连接形成一簇等值线，从受力点出发，沿等值线的脊线形成一条传递通道，定义为结构的主传力路径，如图2所示。

2 承载性能评价与优化

传力路径是力在结构中传递规律的集中体现，其轨迹主要受结构外形轮廓的影响，通常越靠近传力路径的区域对结构整体刚度的贡献度越大，因此，研究传力路径及结构外形轮廓上应变能系数的变化规律，建立承载性能评价方法，可找到结构的薄弱环节，为优化提供指导。

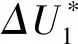
以某异形板为例，如图5a所示，将其左端固定，右端施加力F，计算得到的主传力路径用黑色箭头表示，传力路径上U*变化如图5b，载荷在传递到区域1的M点时U*发生突变，随后在MN段快速下降，经过N点后再次发生突变，开始缓慢下降至支撑点。因此可知，力在区域1传递过程中，U*值衰减较快，该区域属于薄弱区域，需要通过增加材料以提高相对刚度。此外，理论上U*在传力路径方向连续变小，而图6a区域2的U*由大变小再变大，表明该区域存在材料冗余，阻碍了载荷的传递，可以通过减少材料来提高载荷传递的顺畅度。

为了改善结构的整体承载性能，本文提出力流导向的结构设计方法，以传力路径理论为基础，结合承载性能评价结果及优化建议，将材料沿传力路径布置，并增加相应的减重孔及相关特征，实现结构承载性能的优化，具体设计思路如图6所示。

3 算例：控制臂

3.1 控制臂结构介绍

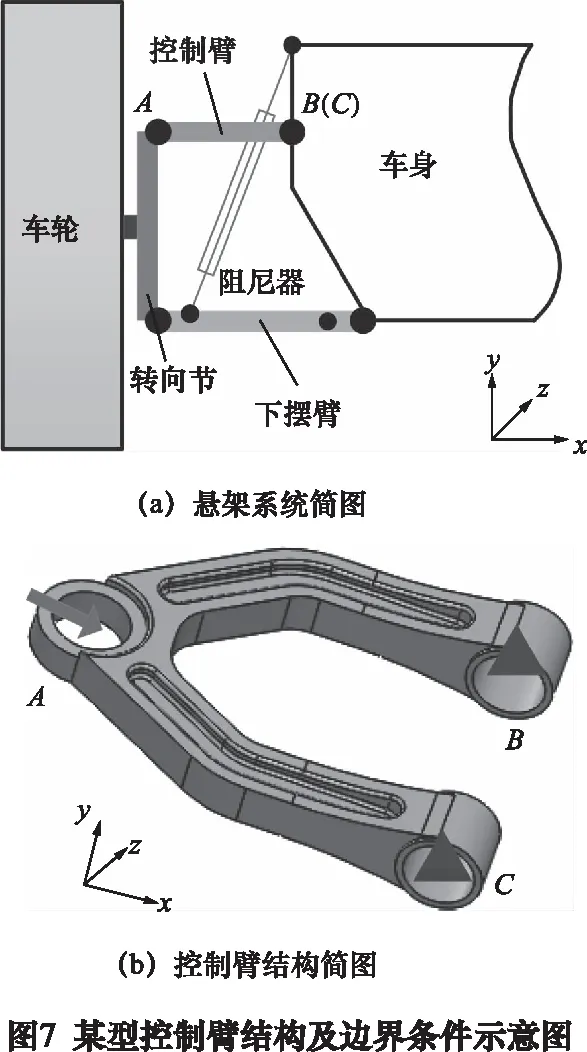
控制臂在汽车的安装位置如图7a所示，具体结构及边界条件如图7b所示，材料为铝合金A356.1，弹性模量为72.4 GPa，泊松比为0.33，密度为2 680 kg/m3，控制臂的右侧两圆柱孔B、C与汽车车架直接相连，在分析时可以等效为固定约束，左侧圆柱孔A与转向节连接，可以等效为销轴载荷。本文以汽车车轮侧撞到马路沿时控制臂的受载情况为例进行传力路径分析，此时圆柱孔A受到沿x方向的载荷3 062.36 N。

3.2 承载性能分析

由于控制臂的载荷传递路径受两支腿形状的影响较大，为了提高计算效率，提取控制臂横截面作为研究对象，计算得到主传力路径如图8所示，可知，载荷从左侧圆柱孔出发，在支腿内侧逐渐传递到支腿外侧，到右侧圆柱孔终止，传递方向变化较大的区域位于支腿拐角处，即区域2。

通常更关注力在结构外轮廓的传递规律，本文进一步分析控制臂支腿内侧(图8路径1)和外侧(图8路径2)的承载性能，得到两条路径的U*变化图如图9所示。

在AO段，路径1上的U*明显大于路径2，而在OB段U*则小于路径2，表明载荷传递到O点之前控制臂内侧承担的刚度大于外侧，而O点之后外侧刚度贡献度更大。在路径1上，U*始终以一定的速率均匀下降，经过K点(对应图8区域2)后，下降速率明显降低，表明区域2左侧材料承担的载荷大于右侧，因此区域2左侧的应力值高于右侧，这主要是由于区域2的拐角阻碍了力流的传递，进而导致力流向控制臂支腿外侧方向传递；而在路径2上，U*先以一定的速率均匀下降，在到达M点后，开始缓慢上升，随后再次下降，表明力流传递到M点时受到了控制臂外侧拐角的影响，导致力流传递速率明显降低，而经过M点后，由于外侧拐角和内侧力流的综合影响，使路径2上的U*逐渐变大，直至N点后开始均匀下降，理想的传力路径认为U*始终均匀下降，因此，MN段U*的上升表明区域3(图8)存在冗余材料，影响了力流的正常传递，在结构设计过程中应该考虑去除。

综上分析可知，控制臂支腿内外侧的力流传递不均匀，主要是由于控制臂支腿拐角处结构设计不合理导致载荷在传递到拐角处时方向发生了突变，建议将支腿外侧材料向内侧偏移，且减小拐角曲线的曲率。

3.3 结构优化设计

为了改善控制臂的承载性能，依据第2节图6思路建立控制臂包络体模型，将控制臂的受载区域和约束区域保留，将其他区域填充为规则的矩形结构，并在圆柱孔B、C之间留出阻尼器的活动空间，得到的包络体模型如图10所示。

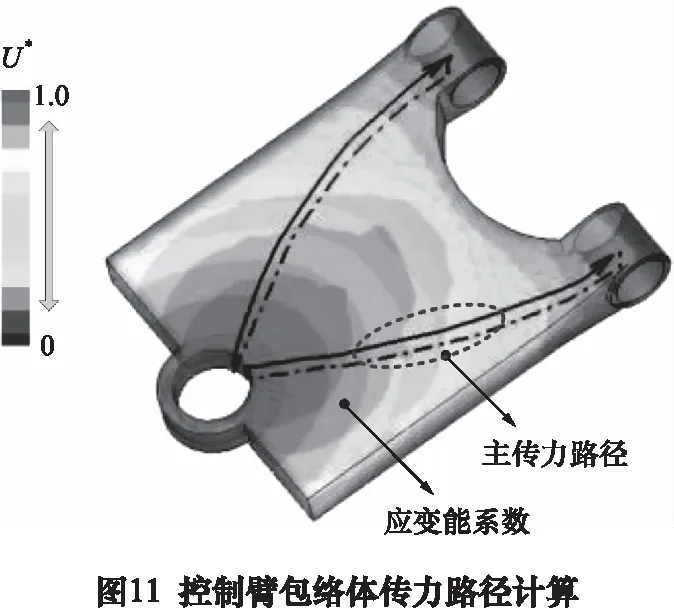
施加与图7相同的载荷和约束，建立包络体有限元模型，计算得到两条主传力路径如图11所示，将材料沿传力路径布置，考虑到加工工艺，将截面设计成矩形，并添加与原结构相同的减重槽，得到新模型如图12所示，其质量由1.01 kg下降到0.92 kg。

3.4 结果对比分析

计算控制臂新模型的U*分布，如图13所示，其主传力路径更靠近支腿内外两侧的中间通道，表明新模型的整体承载性能优于原始模型。

为了说明优化模型的承载性能优势，将优化前后控制臂支腿内侧和外侧承载性能进行综合分析，如图14所示。

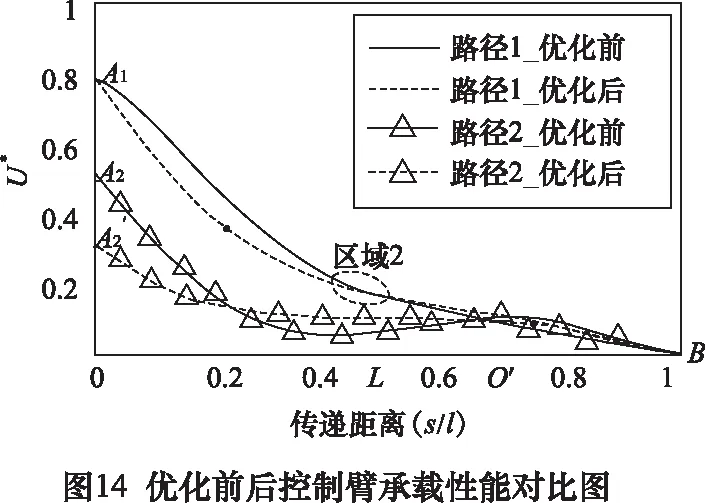
由图可知，优化后控制臂路径1和路径2上的U*变化趋势相似，都是在AO段路径1的U*大于路径2，在OB段小于路径2，不同的是优化后O点的位置更靠近支撑点B，且OB段两条路径上的U*差别很小，表明优化后控制臂支腿的内侧和外侧的承载性能更加均匀，通过优化，刚度贡献度从点A到点B由内侧大于外侧(AO段)逐步转变为两侧(OB段)一致。

从路径1可看出，优化前后初始点的U*一致，但优化后路径前50%(AL段)的U*小于优化前，而后50%大于优化前的路径，说明优化后控制臂支腿内侧的承载性能更加均匀，区域2力流的传递更加顺畅；由路径2可知，优化后初始点的U*远远小于优化前，这主要是优化前控制臂路径2的初始点位于受载圆柱孔与支腿交接处，导致力流传递至此产生了聚集，而优化后力流在该位置的传递相对顺畅，此外，优化后路径上的U*值始终均匀下降，与优化前模型相比，在支腿拐角处不存在冗余材料对力流的阻滞，改善了区域3力流传递的顺畅度。综上分析可知，优化后控制臂的承载性能明显优于优化前。

为了进一步验证优化的合理性，对优化前后控制臂极限工况进行静态特性分析，建立控制臂有限元模型，施加图7所示的载荷和边界条件，得到其最大位移和应力见表1。

表1 优化前后控制臂力学性能对比

由表可知，优化前控制臂的最大位移为0.061 mm，最大应力为17.42 MPa，优化后控制臂的最大位移为0.015 mm，比原模型小了0.046 mm，最大应力为15.92 MPa，比原模型小了1.5 MPa，可知采用传力路径设计的控制臂结构承载性能更优，其刚度、强度分别提高了75.41%、8.61%，质量减轻8.91%。

4 结语

本文基于传力路径理论，提出结构承载性能评价及优化方法，不仅可以给出承载结构局部区域的传力规律，还能评价结构各区域的承载性能，进一步提出将材料沿传力路径布置以最大限度地发挥结构承载性能的设计思路，可实现承载结构的高刚度设计。以某型号控制臂为例进行优化设计，结果表明：优化后控制臂的承载性能得到改善，极限工况下的刚度、强度分别提高了75.41%、8.61%，而质量由1.01 kg减轻到0.92 kg。本文方法同样适用于汽车车身等承载结构的性能评价与优化设计中，其优势在于不需要建立复杂的数学模型进行多次迭代搜索。