某地铁车站开洞梁承载性能试验及数值分析研究

麦家儿 卢晓智 何冠鸿 裴行凯

（广州地铁设计研究院股份有限公司，广州 510010）

0 引言

大多数建筑内部所必需的管线都直接从结构梁下部穿过，为了降低层高和工程造价，工程师多是采用密肋楼盖、宽扁梁、无梁楼盖［1-2］等改变结构形式的方法，但上述方法整体效果并非十分理想。如果在施工时，在建筑顶部梁结构上预留所需的孔洞，使得管线能从中通过，则可在增加建筑物的净空高度的同时，增大使用空间，有助于提升建筑美观效果。然而，梁结构预留的孔洞显然不可避免地会对其结构承载性能及变形特性带来负面影响。孔洞的存在使得梁截面不再保持连续，截面刚度发生变化，可能会导致洞角处的应力集中，致使结构达不到预期承载极限。

《混凝土结构设计规范》［3］（GB 50010—2010）中暂时没有针对腹部开洞的混凝土梁结构的设计有具体规定，但在《混凝土结构构造手册》［4］中，梁腹孔洞周边补强钢筋的计算能找到相关依据。蔡健等［5-8］以孔洞尺寸、弦杆配箍量等为变量对混凝土开孔洞的简支梁进行了系列研究，开展了共计42个矩形孔洞、29个圆形孔洞的混凝土简支梁试件在跨中集中荷载作用下的试验，分析了孔洞的不同属性对开洞梁相关性能的影响规律，为开洞梁的力学性质探究和理论设计方案提供了试验基础。刘荣桂等［9］以孔洞不同的高度位置变换为变量参数，进行了梁腹中部矩形开洞的3个两跨开洞梁和1个实腹梁试件（未开洞）的集中荷载试验，试验结果表明，腹部开洞混凝土连续梁的破坏形态为反弯点处开裂、混凝土的撕裂破坏，构件的终极承载力因上部弦杆的高度增大而相应提高。殷芝霖等［10-11］讨论了开洞梁的承载性能、响应分析和承载能力计算等，这些结论和相关建议为设计提供了重要依据。

当前，梁腹开洞结构在地面建筑中运用较多、在地下工程中运用相对较少，而在地铁车站中，由于需要通过的是环控采用的风管等大型设备，其孔洞尺寸通常要比民用建筑更大，国内外在地铁车站中的应用尚无相关研究。因此，本文对地铁车站顶板大尺寸开洞横梁的承载性能及变形特征展开分析研究，以期为设计及实际工程应用提供必要的依据。

1 试验概况

本文依托的实际工程中，该车站为地下三层岛式车站，车站顶板上覆土为3 m。横梁跨度约为8.65 m，开洞尺寸为2 100 mm×550 mm，此梁腹开洞尺寸需突破现有构造要求。本文对该开洞梁进行突破现有规范的设计，并开展了缩尺模型试验来探究其是否能实现穿孔需求的同时保证结构的安全。

1.1 试件设计

针对某车站结构及所处地层的特点，首先进行正常受载情况下的荷载计算。采用设计荷载组合效应，荷载计算过程共包含满水头及枯水头两种工况。因原型构件尺寸较大，梁高达到1 700 mm，考虑到实验室的反力架限高，本文按1∶2.5的比例制作模型进行试验研究。图1为试件配筋及尺寸详图。

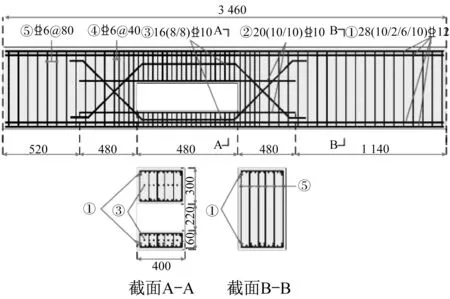
图1 试件配筋及尺寸详图（单位：mm）Fig.1 Reinforcement diagram and sizes of specimen（Unit：mm）

本文采用定理分析法以及量纲分析法求得各相似比，试验模型和原型所用材料相同，几何相似常数Sl=0.4，弹性模量相似常数SE=1，泊松比相似常数Sμ=1，集中力荷载相似常数。

1.2 材料特性

试件采用C40商品混凝土进行浇筑，浇筑同时预备3个边长为150 mm的立方体试块，与试件同条件养护。混凝土28 d立方体实测抗压强度平均值为42.0 MPa，钢筋的力学性能通过单轴拉伸试验测得，结果见表1。

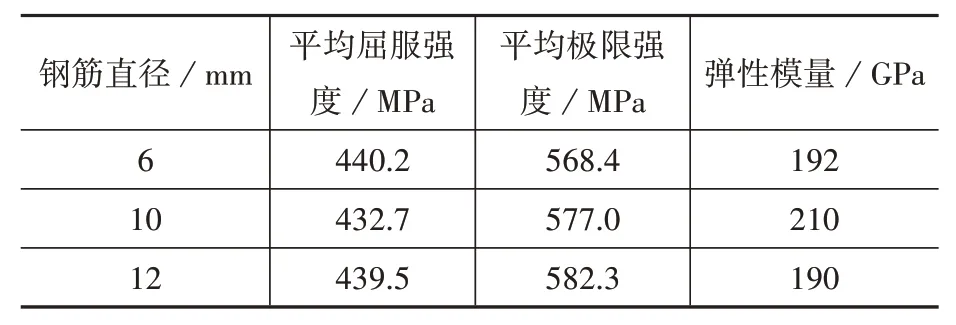
表1 钢筋力学性能Table 1 Mechanical properties of steel bars

1.3 试验加载及测点布置

图2为现场试验装置图，试验在华南理工大学亚热带建筑科学国家重点实验室结构试验中心进行。试件浇捣成型时，在试件梁的两端预留了梁伸臂，用以施加反向弯矩。静力加载中，用于试验的缩尺梁采用液压式千斤顶进行十六分点分级加载，十六分点集中力通过并行控制的最大施加荷载为1 000 kN的8台千斤顶施加，试验梁伸臂端模拟的反向弯矩也是由两台1 000 kN的液压式千斤顶进行加载。

图2 加载现场试验装置图Fig.2 Loading test setup

本次试验采用荷载控制，按正常使用工况下内力所对应的等效荷载转换成千斤顶作用的荷载施加到试验梁上，在达到正常使用工况后保持两端反向弯矩不变，中间千斤顶继续施加荷载，以此探究跨中孔洞处的破坏情况。本文中涉及的荷载，除特殊注明外，均为试验梁顶部中间千斤顶的荷载（单台）。钢筋的应变片布置如图3所示，同一截面至少设置2个应变片（正面为A，反面为B）。每级加载完成后，持荷5 min进行裂缝观察。三个位移计紧贴混凝土梁下端布置，位于在两端支座之间的四等分点上，以上试验数据均通过实验室的数据系统进行集中采集。

图3 钢筋应变测点布置Fig.3 Steel bar strain gauges distribution

2 试验结果及分析

2.1 破坏形态

图4为试件的破坏形态。随着试验的进行，首先在孔洞垂直下方的梁边缘，即上部受拉弦杆的下边缘，开始出现垂直发展的混凝土裂缝。其后，在孔洞的孔角位置处，出现斜裂缝。伸臂梁端顶部出现了斜向发展的受拉裂缝。在试件加载破坏前，试验梁有较大的形变，呈现出了良好的延性。此外，设计人员对构件预留的安全储备较高，试验梁的孔洞没有成为薄弱点而发生脆性破坏。

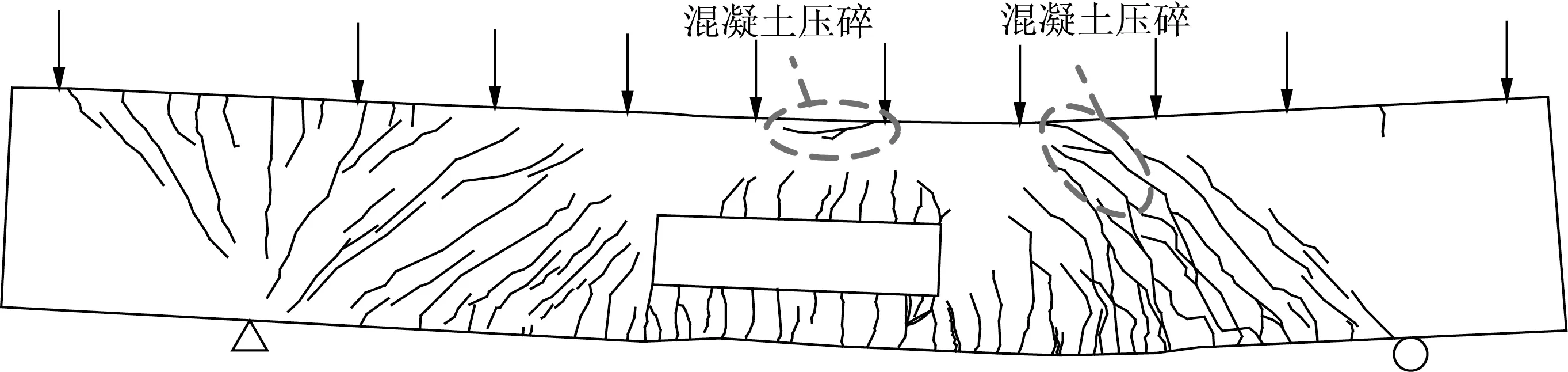
图4 破坏形态Fig.4 Failure pattern

2.2 裂缝宽度

正常使用工况下，孔洞附近裂缝宽度0.08 mm，支座附近裂缝宽度0.04 mm，两者的裂缝开展宽度均处于较低水平。

如图5所示，在8台同步控制的千斤顶荷载作用下，孔洞上方受压弦杆表现出了“小梁”的特性，即受压弦杆上方的纵筋受压，下方纵筋受拉。从图5可知，即使是位于同一截面的应变片，其采集数值也不完全相同。在本次试验中，上部受压弦杆中的确存在反弯点，受压弦杆相当于一道“小梁”，“小梁”顶部和底部钢筋的应变沿着“小梁”纵向有正负的变化，说明存在受拉和受压的转变。

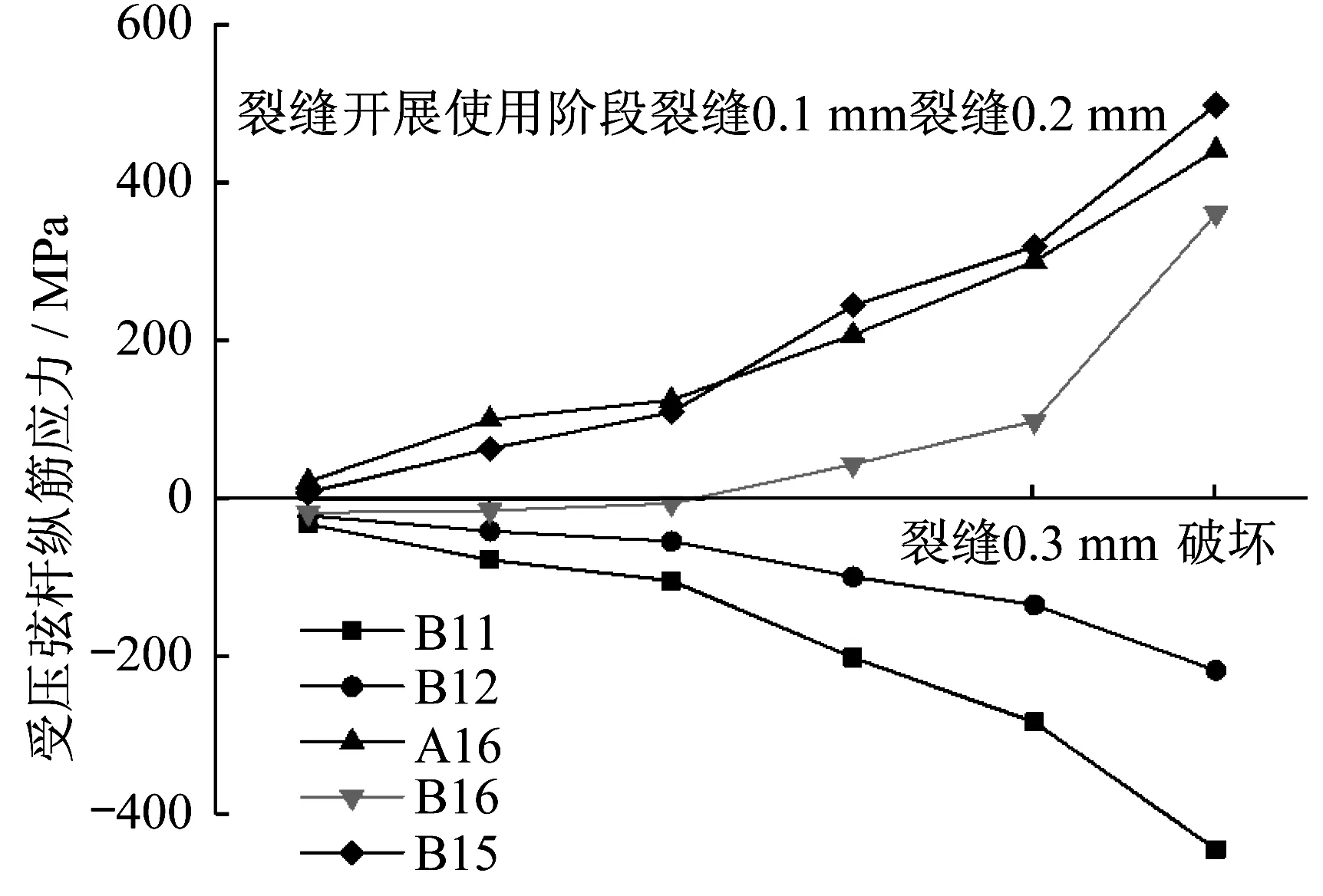
图5 受压弦杆的纵筋应力分布Fig.5 Strain distribution of longitudinal bars in compressed chord

2.3 钢筋应变

图6为试验梁底部纵筋的应力，随着跨中千斤顶施加荷载的增大，梁跨中纵筋应力的增长比较均匀。靠近破坏点位置的纵筋，一开始应力增长较慢。当荷载增长到200 kN时，靠近破坏点附近的纵筋应力迅速增长，此处的挠度也开始迅速增长。

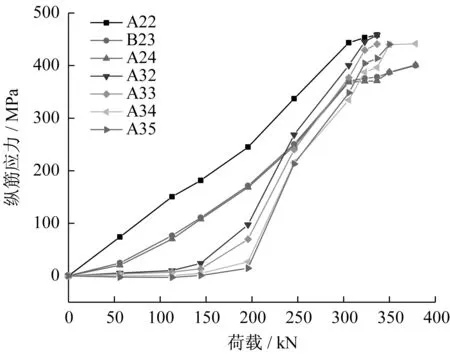
图6 纵筋荷载-应力曲线对比Fig.6 Load-displacement curves of longitudinal bars

图7为试验梁受压弦杆箍筋和破坏位置处箍筋的应力发展曲线图。当跨中千斤顶荷载增加到250 kN时，位于破坏点位置处的箍筋所受应力开始突增，裂缝宽度基本达到0.20～0.30 mm，随即箍筋屈服。相对于破坏位置处附近的箍筋，位于受压弦杆处的箍筋和其直径相同，但是箍筋布置更为密集，拥有较大的抗剪储备。

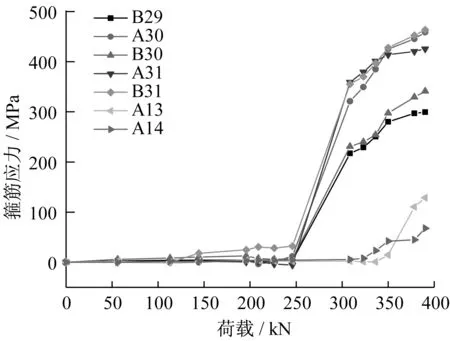
图7 箍筋荷载-应力曲线Fig.7 Load-displacement curves of stirrup

图8为加强斜筋与垂直箍筋的荷载-应力关系。垂直箍筋和加强斜筋同时设置在孔洞两侧时，在相同的荷载作用下，箍筋的应力值均比较低，斜筋的应力值明显要大于箍筋。因此，在实际施工中，尽管绑扎斜筋有一定难度，但还是应当重视孔洞周围加强斜筋的配置。

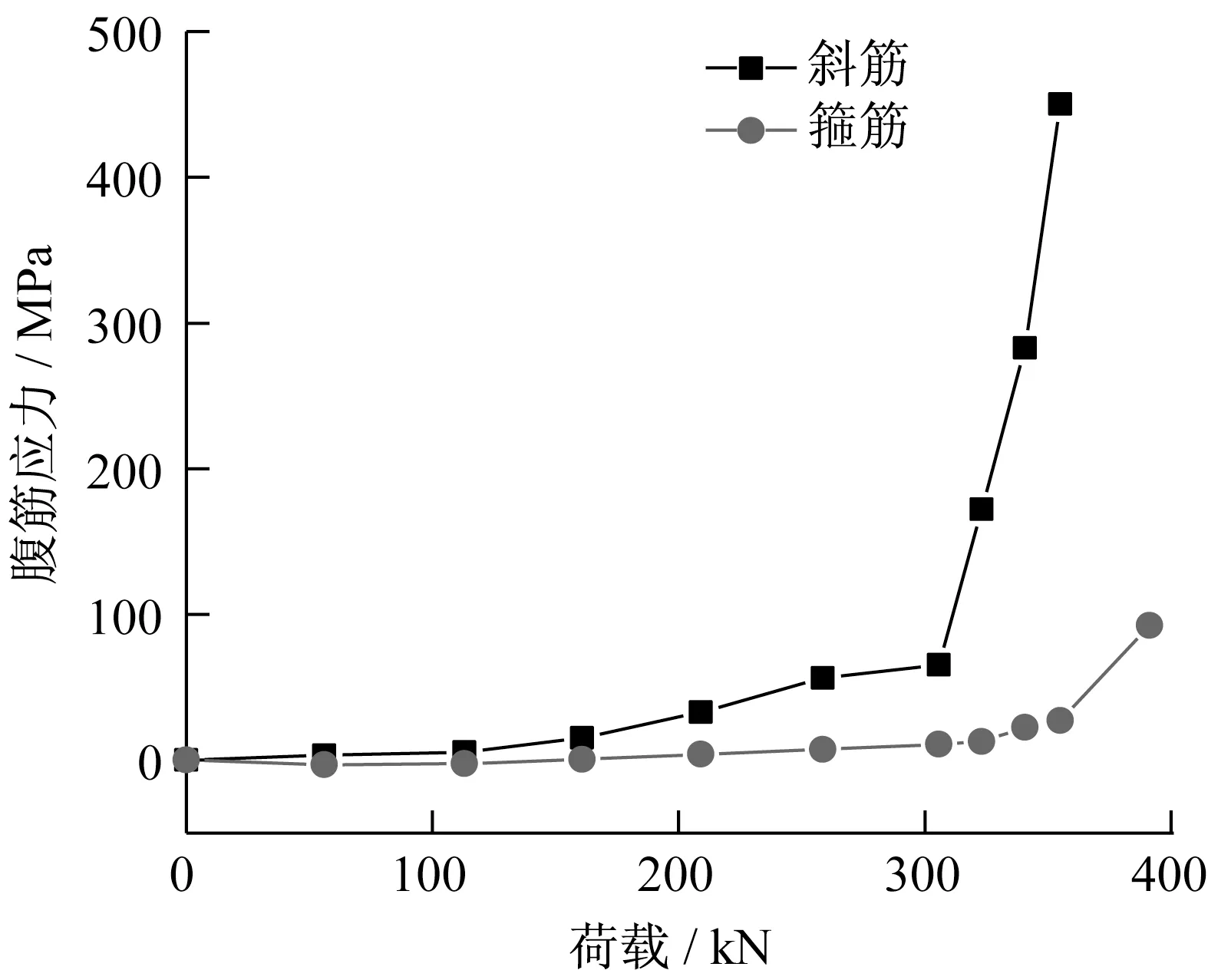
图8 孔侧斜筋与箍筋的荷载-应力曲线Fig.8 Load-displacement curves of tangential and stirrups besides the opening

2.4 变形分析

图9为荷载-跨中挠度曲线。混凝土在尚未出现裂缝之前，荷载-挠度曲线呈现出线性增长的趋势。在荷载增加到320 kN后，此时试验梁屈服，缓慢进入破坏阶段，竖向挠度增加加快；当荷载达到400 kN时，构件无法继续持载，试验梁顶部混凝土压碎，标志着构件破坏。

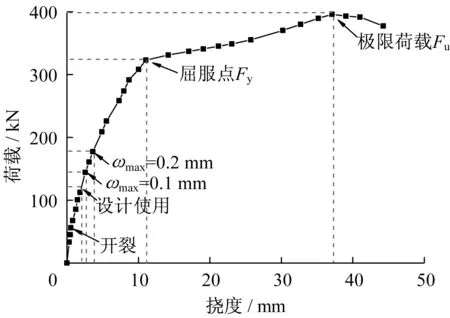
图9 荷载-跨中挠度曲线Fig.9 Load-mid span displacement evolving curve

图10为试件在对应不同荷载水平下的挠度分布图。本次试验，构件的变形曲线与一般受弯构件的变形曲线较为不同。相比对于未开洞的普通梁，孔洞的存在对梁的截面刚度产生了一定影响。因配置了较密的箍筋及腹筋，孔洞附近B点的抗剪能力得到了一定程度的加强。对于C点，由于此处的剪力本身也比较大，且没有对其进行钢筋加固，所以试验的现象表明此处的混凝土压碎现象较为严重，此处也是产生最终贯通斜裂缝的位置。

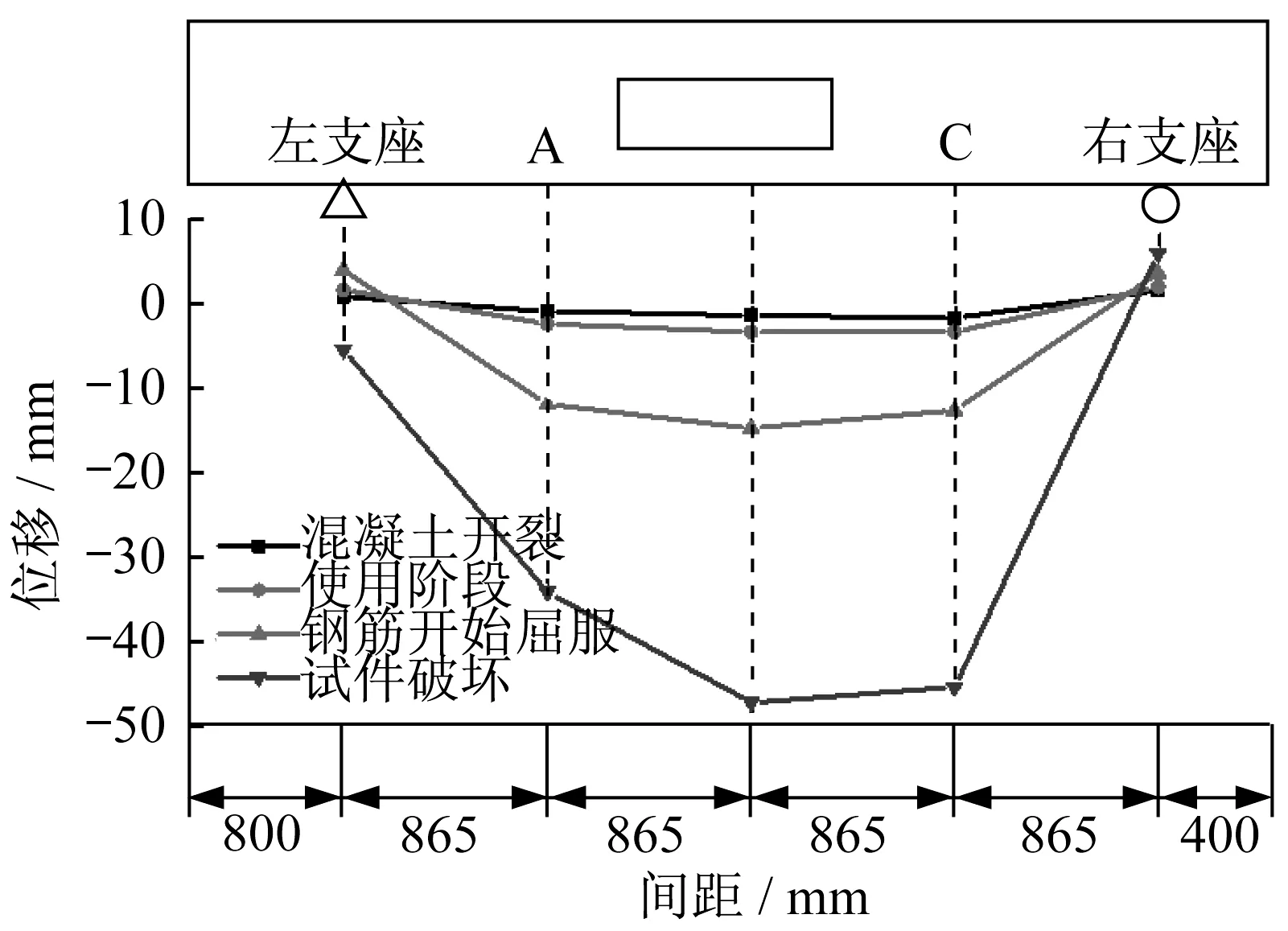
图10 试件沿梁轴线的位移分布Fig.10 Displacement distribution along length

3 数值模拟

3.1 模型建立

采用Abaqus有限元软件，根据缩尺试件的尺寸建立有限元模型进行分析计算，如图11所示。钢筋和混凝土的本构均选用《混凝土结构设计规范》［3］（GB 50010—2010）规定的本构，为反映真实加载情况，边界情况和加载过程均与试验过程统一。

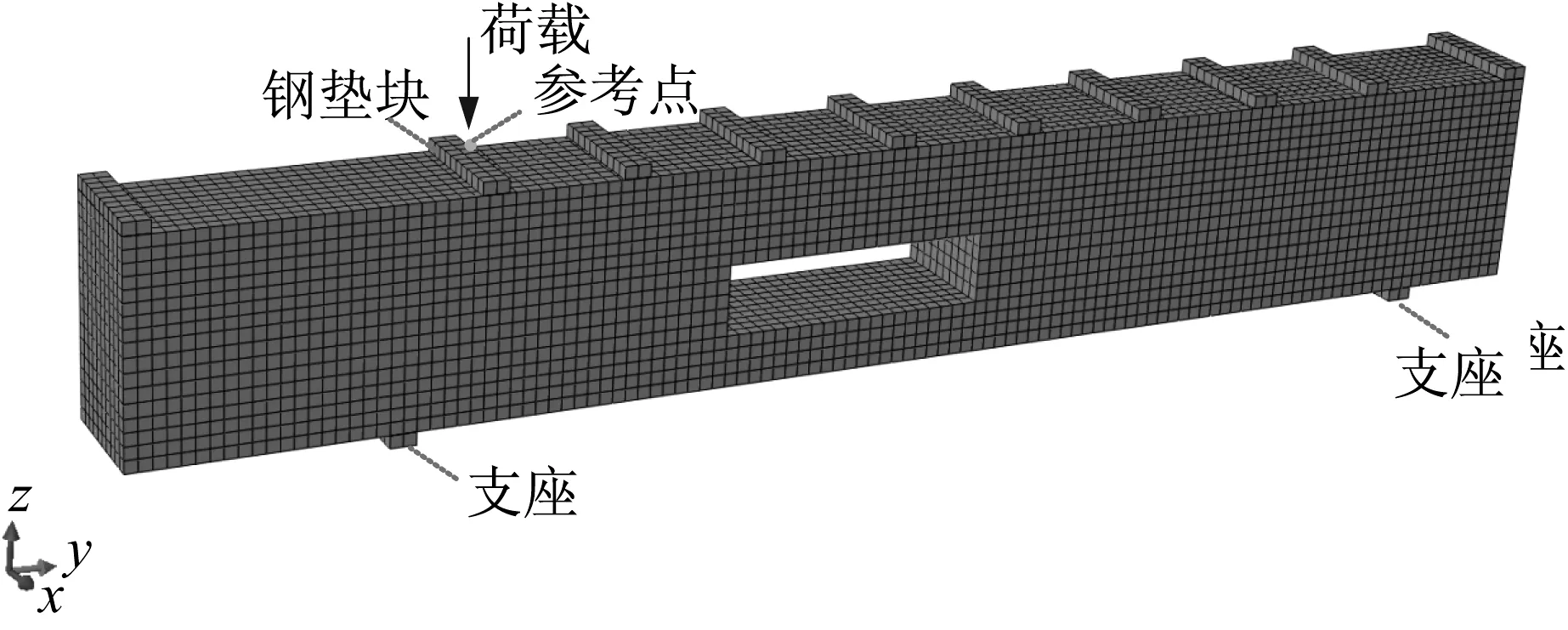
图11 静力加载模型边界Fig.11 Static loading boundary conditions of FEM model

3.2 承载力与破坏形式对比

图12分别为试验与有限元计算的荷载-跨中位移曲线。在初始阶段，试验曲线和数值计算的曲线基本吻合，这时整个构件基本处于弹性阶段。随着试验的不断进行，混凝土开裂，构件的截面刚度下降，塑性开始出现。经分析求得，试验的屈服荷载为320 kN，有限元计算屈服荷载为285 kN，计算所得的屈服荷载略小于试验的屈服荷载。

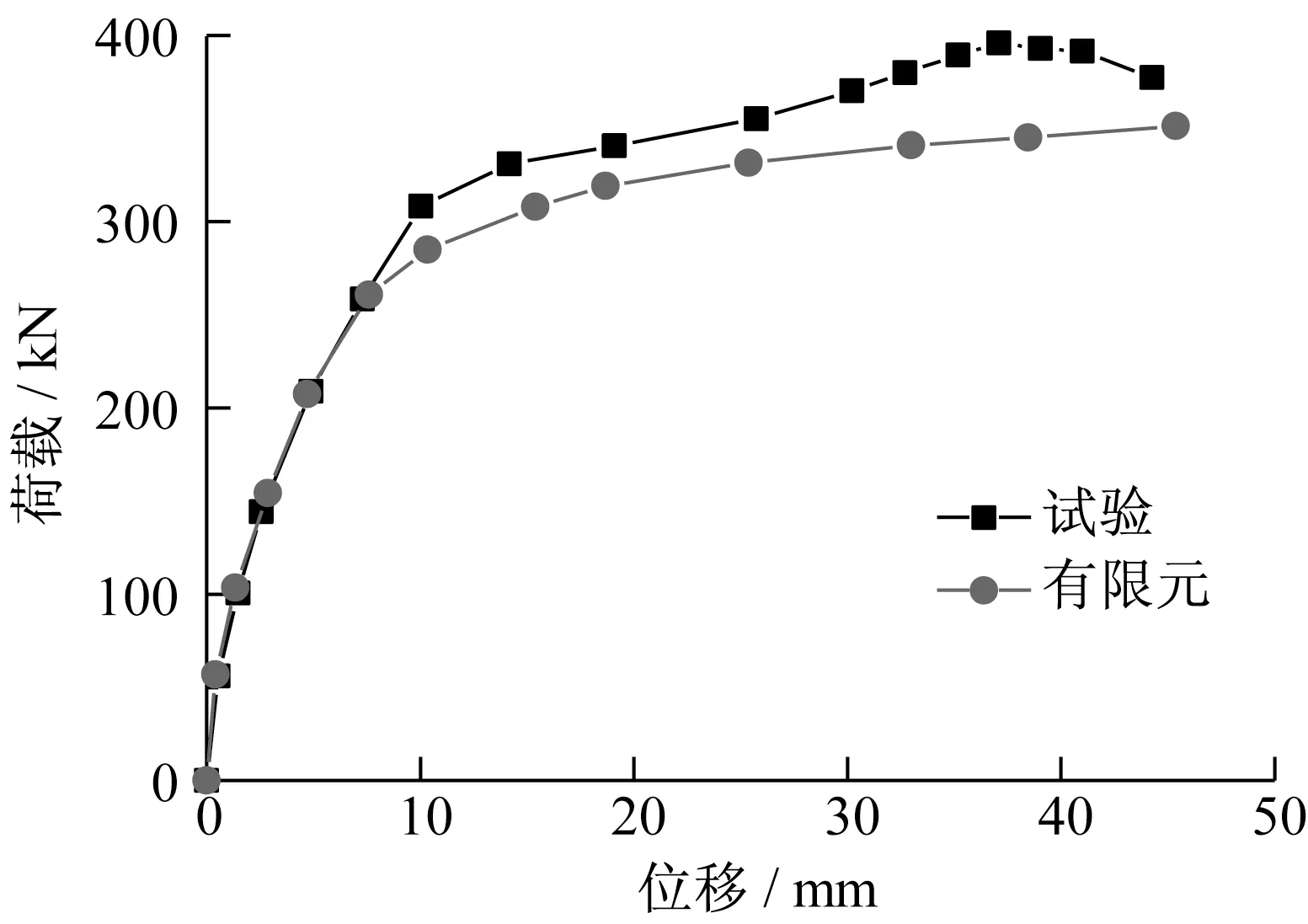
图12 荷载-位移曲线对比Fig.12 Load-displacement curves between test and modeling

计算结果与实测结果在屈服后阶段略有偏差，这是由于在进行加载时，数值模型中所采用的材料本构为规范所规定的本构，实测的材料强度要略大于规范规定的材料强度，且模型计算时，忽略了钢筋和混凝土之间黏结滑移的影响。总体而言，有限元计算的结果和试验结果较为接近，表明采用Abaqus有限元软件对试验过程进行模拟计算的结果较为可信。

3.3 工作机理研究

为研究试验构件的内力分布及应力发展情况，本文选取了几个具有代表性的关键时机节点：正常使用点（144 kN）、构件屈服点（285 kN）和最终破坏点（350 kN），荷载均为中部加载点施加荷载。

3.3.1 正常使用点

图13为构件在正常使用荷载下的应力应变云图。因模拟连续梁所受反向弯矩，伸臂端混凝土受拉，该处顶部混凝土塑性变形较明显。开洞梁的承载力远未达到极限状态，仍可继续承载，但此时混凝土已开裂。

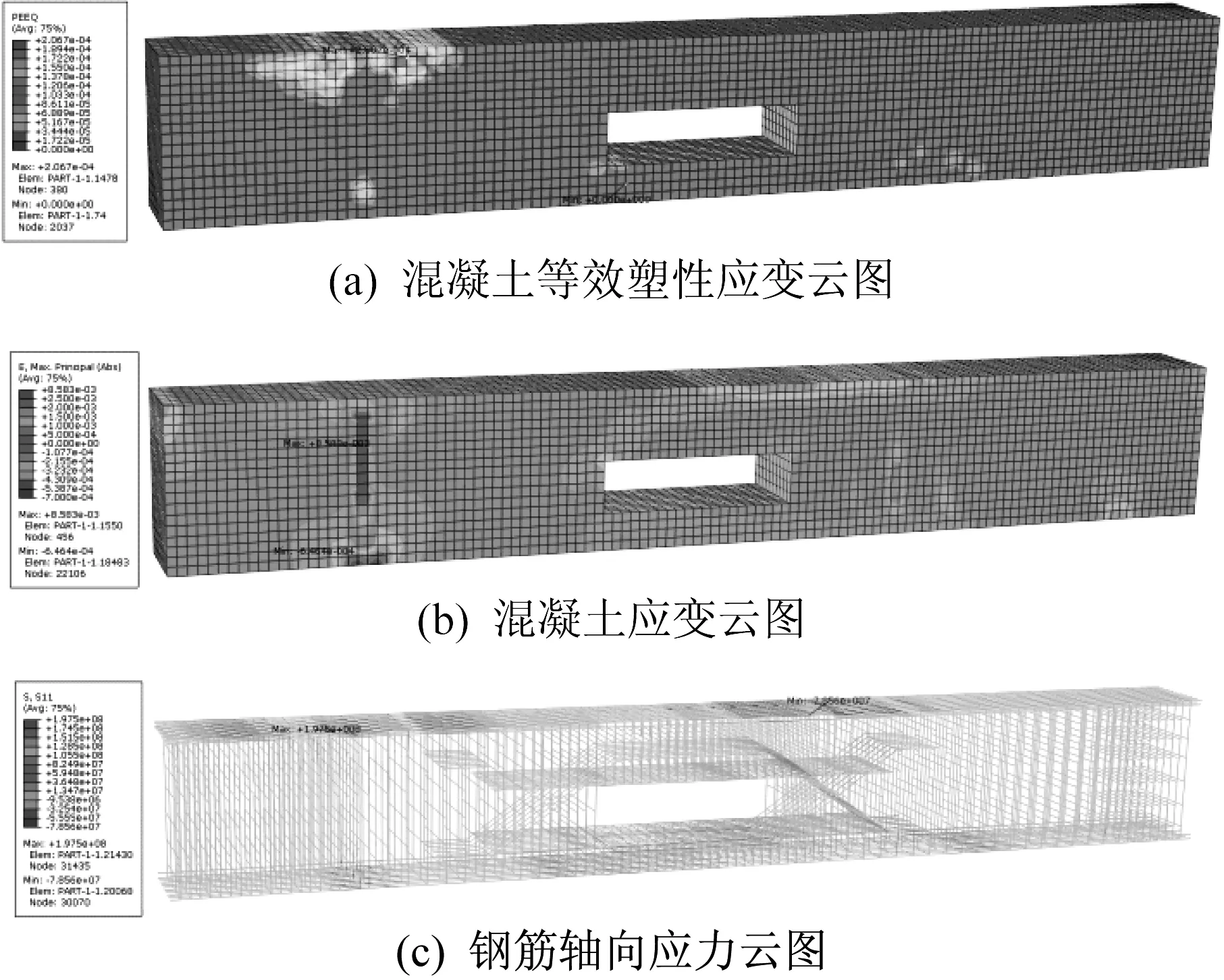
图13 正常使用工况下应力应变云图Fig.13 Stress-strain contours under normal conditions

3.3.2 构件屈服点

图14为构件屈服阶段（285 kN）下应力应变云图。在此阶段，试验梁底部纵筋多数已经屈服，位于受拉弦杆及受压弦杆内的纵筋也有部分位置屈服，混凝土的等效塑性峰值出现在位于孔洞右侧0.6 m处，此处有部分箍筋屈服，部分混凝土开裂严重且接近压碎。

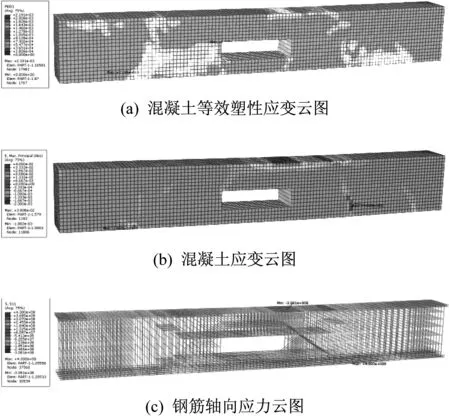
图14 构件屈服工况下应力应变云图Fig.14 Stress-strain contours under yielding conditions

3.3.3 最终破坏点

图15为构件最终破坏工况（350 kN）下应力应变云图。位于开孔洞右侧区域及右上方的混凝土已受较大压应变，此处混凝土受压破坏，这与试验观测到的结果一致。

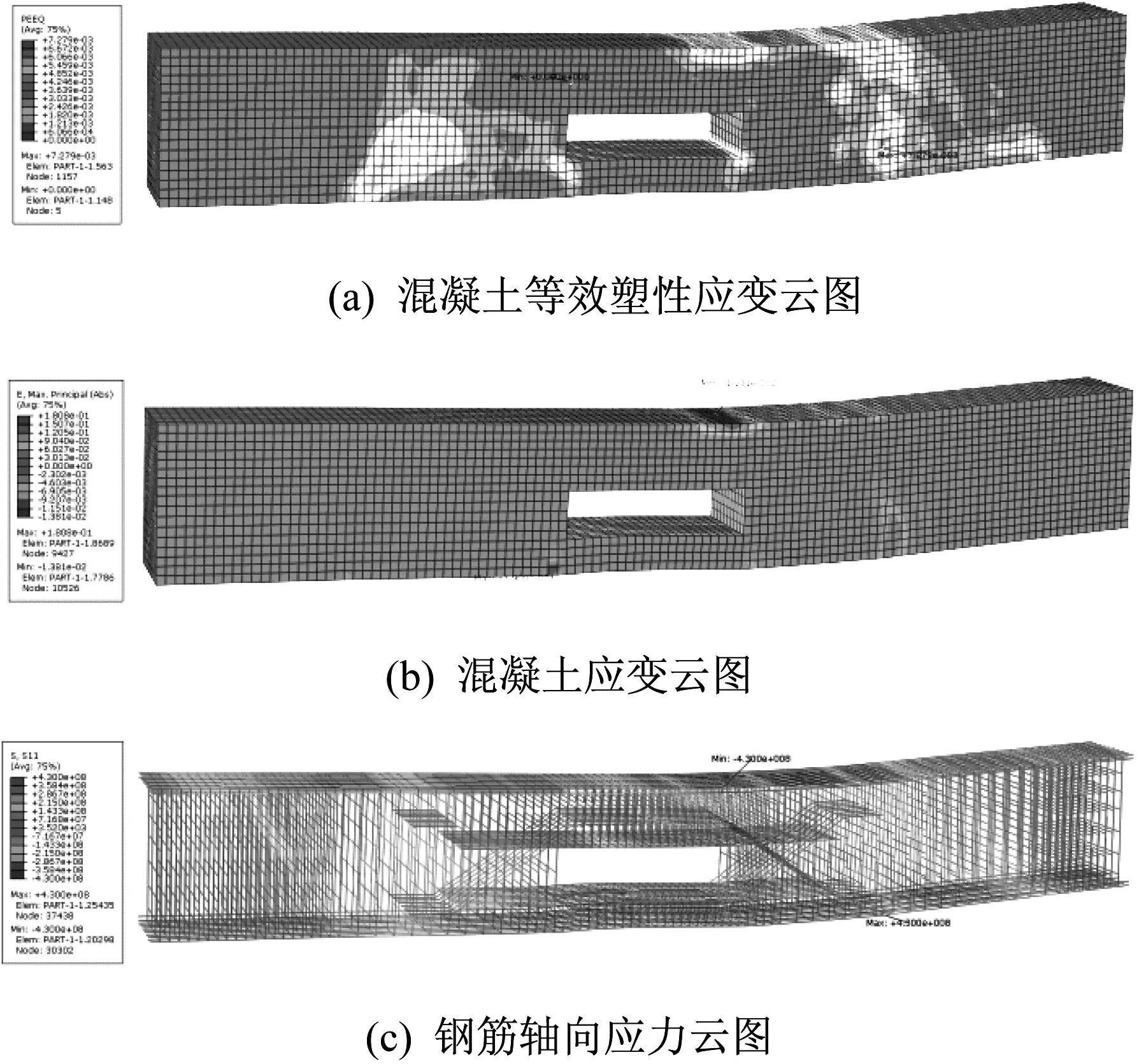
图15 构件最终破坏工况下应力应变云图Fig.15 Stress-strain contours under ultimate conditions

4 结论

（1）开洞梁试验构件破坏前，构件经历了较大形变，破坏征兆较为明显，试验构件表现出了较为理想的延性破坏。破坏时弯剪裂缝向下延伸，裂缝宽度不断加大，出现混凝土掉块，直至钢筋拉断，导致试件丧失承载能力。

（2）在正常使用工况下，试件梁混凝土上出现的裂缝较少，开孔周围布置了加密的箍筋和斜筋，孔洞未产生明显的应力集中现象导致其成为薄弱环节而提前破坏。试验结果表明：试件的承载力极限相较于试件的设计使用荷载有较大富余，足尺构件满足正常使用要求。

（3）通过钢筋应力分析表明，相比较于孔侧垂直箍筋，加强斜筋的抗剪承载更大，能够较好地控制开洞梁斜裂缝开展。因此，在孔洞周围合理地布置斜筋，优化不同种类钢筋布置方式，能够有效加固孔洞这一薄弱环节，大大缓解应力集中现象。