基于Matlab/Simulink的PI调节器建模分析与限幅特性仿真研究
张厚升, 朱胜杰, 邢雪宁, 杜钦君, 赵艳雷
(山东理工大学电气与电子工程学院,山东淄博255000)
0 引 言
对于自动控制系统来说,系统的稳态精度和动态性能指标常常是互相矛盾的[1-2],依据自动控制理论,要解决这个矛盾,必须设计合适的动态校正装置,用来改造系统。动态校正的方法较多,对于一个自动控制系统来说,能够符合要求的校正方案也不是唯一的。在自动控制系统中,对于带电力电子变换器的直流闭环调速系统[3-4],传递函数阶次比较低,一般采用PI调节器[5-8]就能完成系统动态校正的任务。
许多初学习者对于PI调节器的特性理解不够深入,尤其是在采用Simulink进行自动控制系统建模仿真的时候[9-10],调试的过程中出现问题最多的也是PI调节器,甚至得不到正确的仿真波形。通常,利用Matlab/Simulink对PI调节器进行建模有几种不同的形式[11-12],比较常见的一种是基于PI调节器传递函数建立的仿真模型,另一种是带积分限幅的PI调节器仿真模型,对于这些不同的仿真模型,很少有人去关心其特性,只是根据PI调节器建立相应的系统仿真模型并进行仿真,仿真结果有时候会存在一些问题,却找不到原因。本文旨在对采用PI调节器传递函数仿真模型和带积分限幅的PI调节器仿真模型进行特性分析与建模仿真,研究其性能上的差异,以便使用者在进行自动控制系统Simulink仿真建模时选择合适的PI调节器模型及其参数。
1 PI调节器的传递函数与特性分析
依据控制理论的相关知识,比例控制具有控制的快速性,但只能实现系统的有静差调节;积分控制可以实现系统的无静差控制,但系统的快速性却较差,如果要实现系统的稳态精度高,同时又要实现动态响应快,可以把比例和积分两种控制结合起来[1-2],即采用PI调节器,实现系统的无静差快速调节[13]。
PI调节器的输出由比例和积分两个部分叠加而成,其输入-输出的关系可以描述为
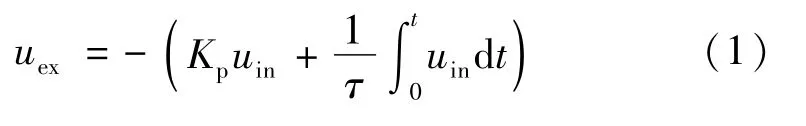
式中:Kp为PI调节器的比例放大系数;τ为PI调节器的积分时间常数。
PI调节器的传递函数可以表示为[1-2]:

如果令Ti=Kpτ,则PI调节器的传递函数也可以表示为
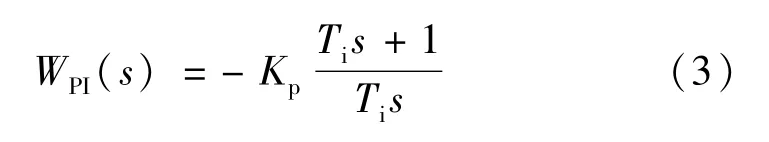
或者
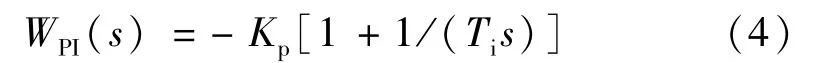
式中,Ti是微分项中的超前时间常数。这里需要注意,Ti和积分时间常数τ的物理意义是不同的。
依据式(3)、(4),可以用Simulink建立两种不同的PI调节器仿真模型,但是这两种仿真模型的效果是不一样的,后文将会展开深入研究。
采用模拟控制时,在自动控制系统中,常用的PI调节器可以用运算放大器来实现,如图1所示(采用数字控制时的基本原理类似,本文以模拟控制为主进行分析)。图中uin和uex分别为PI调节器输入电压和输出电压,在图1中,由于运算放大器的反相作用,uin和uex的极性是相反的(图中所示的极性表明调节器的输入信号和输出信号是反相的)。电阻Rbal为平衡电阻,接在运算放大器的同相输入端,通常其值的大小为运算放大器反相输入端各电阻的并联值。依据运算放大器的输入-输出关系,可以得到
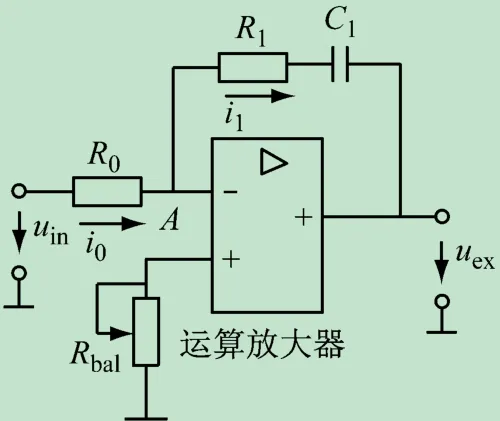
图1 PI调节器电路原理图
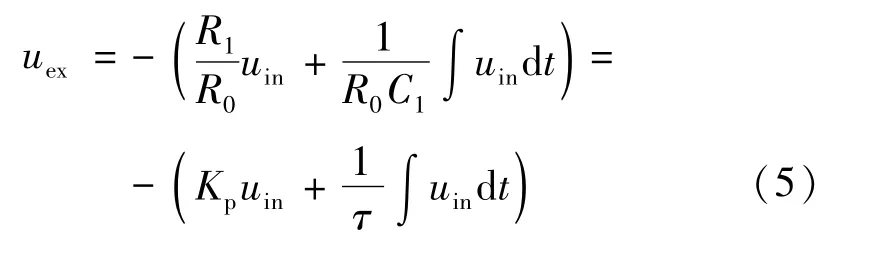
式中:Kp=R1/R0;τ=R0C1。
在零初始状态和方波输入电压uin下,PI调节器的输出电压uex的时间特性如图2所示。当t=0时突加输入电压uin,由于比例部分的作用,输出量uex立即响应,马上跳变为uex(t)=-Kpuin,实现了系统的快速响应;之后uex(t)按照积分规律增长,uex=-[Kpuin+(uin/τ)t],在t=t1时,输入电压uin突变为零,uin=0,uex=(uin/τ)t1,PI调节器的积分调节作用使其后级的电力电子变换器输出稳态电压,足以克服系统的负载电流压降[2-4],实现系统的稳态转速(或者其他变量)无静差调节。
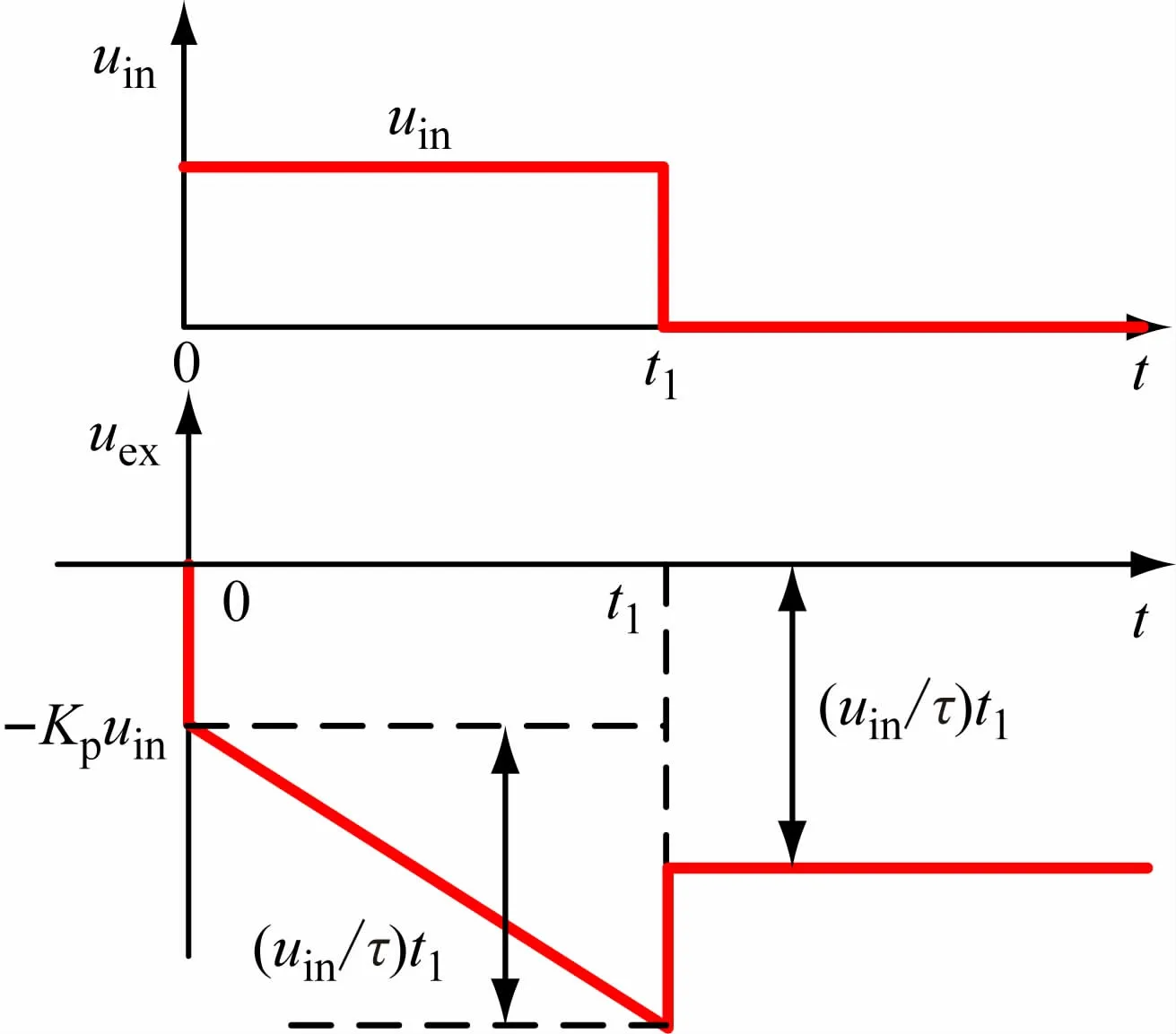
图2 PI调节器的输入-输出特性
结合图1,从图2的特性图上也可以看出PI作用的物理意义。由于系统处于零初始状态,突加输入电压uin时,对于电容C1来说,由于电容两端的电压不能突变,相当于两端瞬时短路,此时PI调节器相当于一个单纯的反相比例放大器,所以输出电压会立即跳变到uex=-Kpuin,保证了系统的快速响应。此后,电容C1被充电,输出电压uex开始积分,其数值线性增长。由图2可见,如果输入电压uin一直存在或者输入电压uin的值比较大(该值决定了积分的斜率),电容C1就不断被充电,不断进行积分,直到输出电压uex达到运算放大器的限幅值-uexm为止,此时就称运算放大器饱和。为保证线性放大作用并保护系统各环节,对具有积分作用的运算放大器设置输出电压限幅是非常必要的。在实际的转速闭环控制系统中,当转速上升到给定值时,PI调节器的输入电压uin=0,此时积分过程也就停止了。对于图2而言,在PI调节器的调节过程中,如果不考虑运算放大的饱和作用,在t=t1时,输入电压uin=0,此时PI调节器失去比例放大作用,因此系统的输出电压会有所降落,系统成为积分器维持电容C1上的电压输出,亦即积分电压值输出uex=-(uin/τ)t1。
如果采用数字控制,可将式(1)或者式(5)的时域方程离散化为差分方程,用数字PI算法实现,但是其物理意义还是一样的,在此就不再赘述。
由此可见,PI调节器综合了比例控制和积分控制两种控制规律的优点,扬长避短,互相补充,可以实现系统的动态快速控制和稳态无静差控制。在闭环调速控制系统中,负载的扰动会引起输入偏差电压Δun的变化,图3给出了PI调节器的输入输出的动态过程,不妨假设闭环调速系统的输入偏差电压Δun的波形如图3所示,采用PI调节器的输出电压uc的波形③由两部分叠加而成,即与输入偏差电压Δun成正比的波形①,输入偏差电压Δun的积分波形②,由此可见,控制电压uc既具有快速响应的性能,又足以消除系统的静差[2],除此之外,PI调节器还是提高系统稳定性的校正装置,因而PI调节器在调速系统[3-4,14]和其他控制系统中得到了极为广泛的应用。
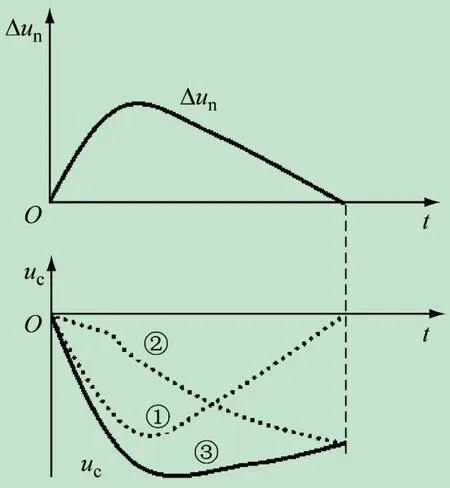
图3 闭环系统中PI调节器的输入和输出动态调节过程
2 PI调节器的Simulink建模与性能研究
在自动控制系统中,PI调节器的传递函数既可以用Matlab语句表达,也可以用Simulink的传递函数模块和比例模块、积分模块表达,使用Simulink模块不仅方便,而且可以反映调节器的输出限幅作用,但按照式(3)用Simulink传递函数模块和按照式(4)用比例积分模块建立的仿真模型的性能和效果是不一样的,下边分别进行研究。
2.1 PI调节器传递函数模型
依据式(3)用Simulink传递函数模块建立的PI调节器的仿真模型如图4所示。
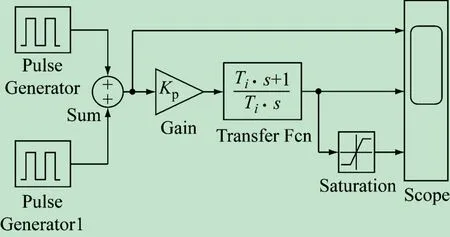
图4 PI调节器传递函数Simulink仿真模型
模型中用放大模块Gain和传递函数模块Transfer Fcn组成PI调节器的传递函数形式[11-12]。放大模块Gain的放大倍数为Kp,利用传递函数模块Transfer Fcn来设置PI调节器的积分时间常数,两个脉冲模块Pulse Generator和Pulse Generator1经过信号求和模块Sum产生脉冲宽度可以调整的输入信号,作为PI调节器的输入源,以此观察PI调节器在偏差输入信号下的动态响应。Saturation模块用来设置限制PI调节器的输出电压幅值,用示波器Scope观察PI调节器在有、无限幅作用情况下的输出电压的波形,并分别与PI调节器的输入信号进行比较。
系统的仿真参数见表1,选择ode45算法,仿真时间设为2个周期(6 s),仿真结果如图5所示。

表1 PI调节器传递函数模型的仿真参数
图5(a)为PI调节器的输入信号波形,图5(b)为PI调节器无限幅的输出波形,图5(c)为PI调节器经过限幅后的输出波形,由图5(a)、(b)可见,在输入信号脉冲值为“-1 V”的时间段内(t=0~0.6 s),由于比例放大系数Kp=2,因此PI调节器的输出在t=0时从2 V开始在积分作用下线性增长;在输入信号脉冲值为“0 V”的时间段内(t=0.6~1.5 s),PI调节器的输出维持t=0.6 s的输出值20 V不变;在输入信号脉冲值为“1 V”的时间段内(t=1.5~2.1 s),由于输入信号变负,积分器开始反相积分,PI调节器的输出值开始降低。在t=2.1 s时,输入信号再次变为0,此时PI调节器输出维持不变。由图5(a)、(c)可见,如果PI调节器的输出增加了限幅环节,那么PI调节器的输出幅值就会被限制在设定值±10 V之间。
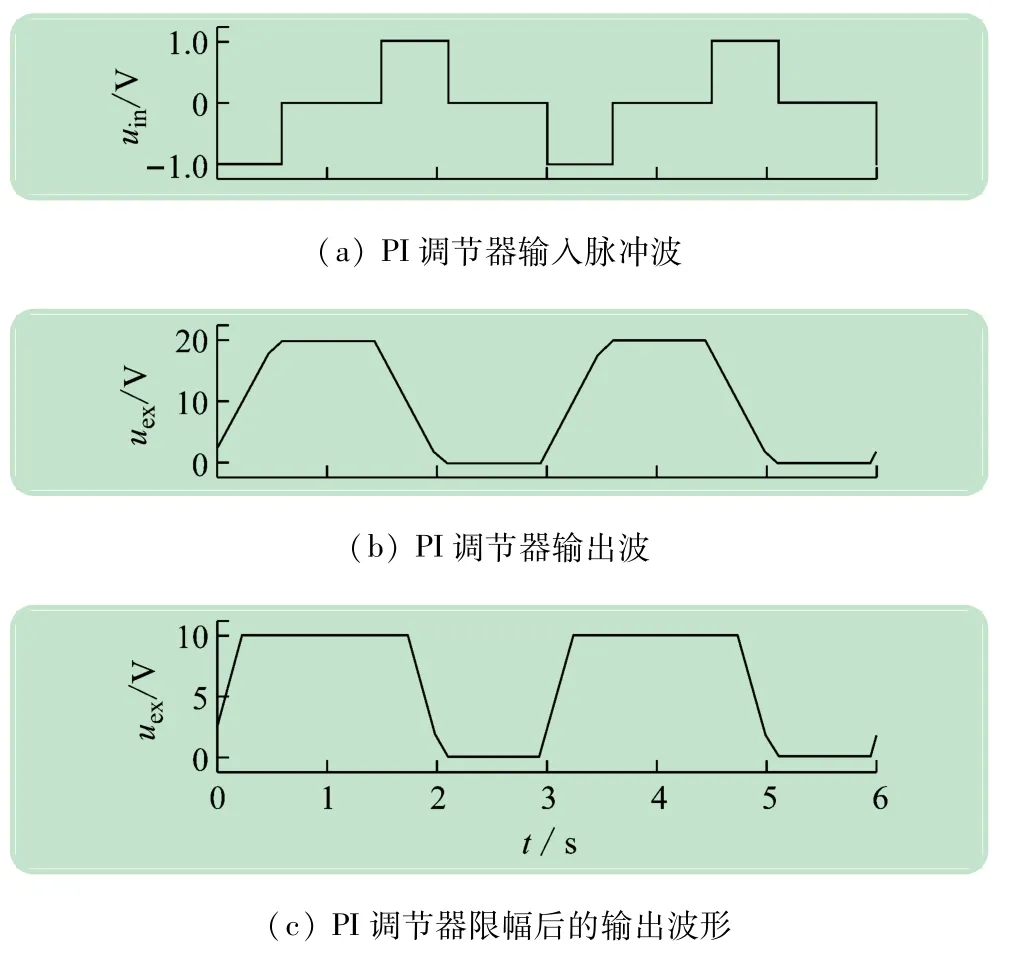
图5 PI调节器传递函数模型的仿真波形
由图5可知,PI调节器在正或者负的输入信号作用下,其输出信号也随之增加或者减少;当输入信号变为0 V时,PI调节器能维持前一时刻输入变为0 V时的输出值,该输出电压值与积分的时间(脉冲宽度)密切相关。一般情况下,自动控制系统都是采用PI调节器来消除系统的误差,在系统输出产生误差时,PI调节器能立即产生可消除误差的控制信号。从图5所示的输出波形上也可以看出,在系统存在误差时,也就是PI调节器存在输入电压信号时,PI调节器能够迅速按照积分规律产生输出控制信号,在这里,PI调节器的积分时间常数Ti影响输出控制信号上升或者下降的斜率(积分曲线的斜率),而且能够在误差为0(输入电压为0)时,保持之前PI调节器的输出状态,PI调节器的比例系数Kp抬高了PI调节器的输出信号值,起着迅速加快调节的作用。
对于图4所示的Simulink仿真模型而言,PI调节器的输出信号是随着积分时间而增长的,积分时间越长,PI调节器的输出值也就越高,这与实际的PI调节器的工作情况是不相符的。这也是许多研究者建模时所容易忽略的一个问题,导致在采用该模型进行建模仿真时,得不出正确的结果。对于实际的PI调节器而言,不论是模拟的PI调节器,还是数字式的PI调节器,都会对积分环节加上幅值限制环节[8-10],使其输出不能随时间无限制的增长。从图5的仿真波形中可以看出,模型中的限幅模块限制了调节器的输出,但是在输出限幅时,调节器的积分作用还在继续起作用,从而使得系统在出现负偏差信号的时候,限幅输出信号的下降时间要滞后于负偏差信号。从图5(b)、(c)可以看出,在t=1.5 s时,无限幅PI调节器的输出信号值从20 V开始下降,但是有限幅环节的PI调节器输出信号却是在t=1.75 s时开始从10 V下降,这也是容易造成自动控制系统超调的原因[15-16]。
2.2 带积分限幅的PI调节器模型
带积分限幅的实用PI调节器仿真模型按照式(4)在Simulink中搭建,式中的积分环节使用Integrator模块来实现[6],该Integrator模块可以限制积分输出的最大值,用Integrator模块搭建的PI调节器的模型如图6所示。图中,可由增益模块Gain1设置PI调节器的比例放大系数Kp,增益模块Gain3用来设置PI调节器的积分时间系数Ki(Ki=1/Ti),积分器Integrator模块的限幅值可以设置成运算放大器的饱和输出值,在仿真模型中设置成了±15 V,对于其他环节的参数,和前面图4的参数基本相同,对该模型进行仿真,所得到的带积分限幅的PI调节器的仿真波形如图7所示。图7(a)是PI调节器的输入电压仿真波形,图7(b)是经过比例放大2倍后的运算放大器输出波形,图7(c)是积分器Integrator模块饱和限幅之后的仿真波形,图7(d)是限幅之后的PI调节器的输出仿真波形。由图7(c)、(d)中可见,由于积分器设置了±15 V限幅值,PI调节器设置了±10 V限幅值,PI调节器的输出限幅值小于积分器的输出限幅值,因此,输入电压信号在1.5 s由0 V变成负值之时,积分调节器的输出值立即开始从正的限幅值+15 V下降,但对于PI调节器来说,其输出值却是在1.6 s的时候开始从正的限幅值+10 V下降,这两个仿真波形之间存在着0.1 s的时间延时,这相当于由运算放大器组成的带输出限幅环节的PI调节器的退饱和延时。如果将积分调节器的限幅值和PI调节器的输出限幅值都设置成+10 V,那么图7(c)、(d)的仿真波形将会完全一致,不会存在时间延迟。所以,在数字PI调节器中,为了减小闭环调节系统的退饱和超调量,通常取积分器的限幅值和PI调节器的输出限幅值相同。
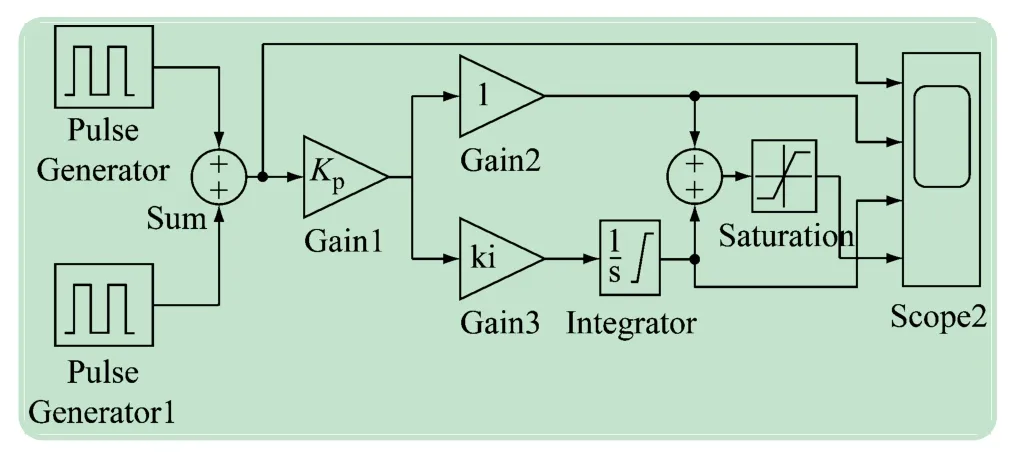
图6 带积分限幅的实用PI调节器仿真模型
比较图5和图7可知,在输入脉冲信号完全相同的情况下,对于带积分限幅的PI调节器模型和无积分限幅作用的PI调节器传递函数模型来说,其输出是不同的,对系统的影响也是不一样的。尤其是对于自动控制系统来说,在进行系统建模的时候,PI调节器采用带积分限幅的PI调节器模型是非常重要的。为了使用上的方便,可以将该模型封装为一个PI控制器子系统,使用的时候直接作为一个分支模块使用就行了,只需要修改其相应的Kp、Ki、积分限幅值、PI调节器限幅值等几个参数即可。这样在将其应用到规模较大的复杂系统时会使得模型变得更加简洁。
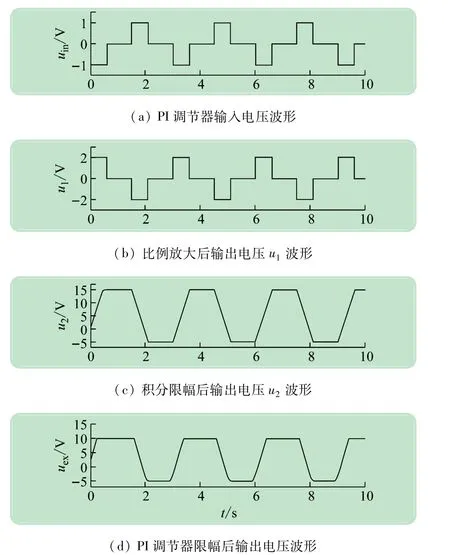
图7 实用PI调节器模型的仿真波形
3 PI调节器输入输出特性的验证
采用带积分限幅的PI调节器模型也可以对PI调节器的输入-输出特性进行验证,调整两个Pulse脉冲,可以将PI调节器的输入脉冲信号调整为正的方波电压信号,如图8(a)所示,在整个动态调节过程中,设置PI调节器一直处于不饱和状态,由图8(c)可见,在0~4 s时间段内,积分器从0开始反相线性积分,到4 s时,输入脉冲信号变为0,积分器停止积分,并维持在-3.2 V。从图8(d)可以看出,t=0 s时,PI调节器的输出就变为4 V,也就是说此时只有比例部分起快速调节作用,随后PI调节器的输出反相线性上升,直至t=4 s时,输出电压信号达到-7.08 V。t=4 s时,PI调节器的输入电压信号变为0 V,对于比例放大部分,已经失去了放大作用,此时PI调节器靠积分器的输出来维持系统需要的稳态输出信号,因此,在t=4 s时,PI调节器的输出信号由-7.08 V升至-3.2 V。从而也验证了PI调节器在方波输入电压信号下的输入-输出特性。
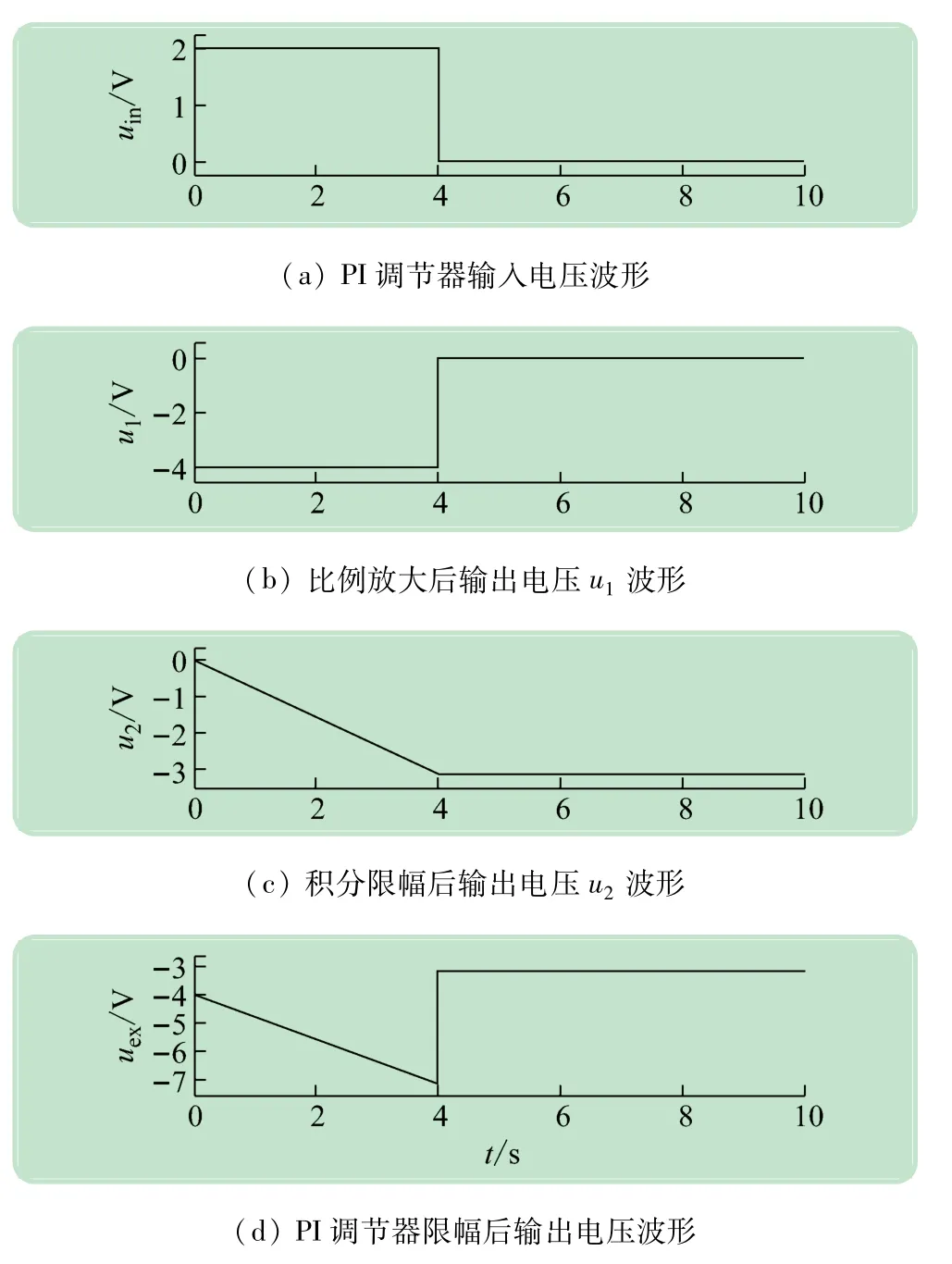
图8 方波电压输入信号下PI调节器的输入输出特性仿真
4 结 语
PI调节器是自动控制系统设计时的一个重要环节,尤其是在建模仿真分析的时候,PI调节器仿真模型构建的好坏将会直接影响自动控制系统的性能,因此建立合理的PI调节的仿真模型至关重要。本文在分析PI调节器的组成及输入输出特性的基础上,研究了其Simulink仿真模型,得出以下结论。
(1)PI调节器可以用式(3)、(4)两种不同的传递函数表示,可以依据这两个公式分别建立PI调节器的仿真模型。
(2)依据式(3),利用Simulink的传递函数模块建立的PI调节器仿真模型,无积分限幅作用,只能对整个PI调节器的输出进行限幅,使得系统在出现负偏差信号的时候,限幅输出信号的下降时间要滞后于负偏差信号,容易导致自动控制系统超调,与实际PI调节器的工作状态存在一定的差异。因此不建议在构建自动控制系统仿真模型时采用该PI调节器仿真模型。
(3)按照式(4),利用Simulink的比例和积分模块建立的带积分限幅的PI调节器仿真模型,与实际PI调节器性能相符,可以灵活的设置积分器和PI调节器的限幅值,能够有效减小闭环调节系统的退饱和超调量。为了使用上的方便,可以将其封装为一个子系统进行使用。
(4)利用带积分限幅的PI调节器仿真模型可以有效的验证PI调节器在方波输入信号作用下的输入输出特性。

