基于卷积神经网络的调制信号识别算法

邵敏兰， 周鸿渐， 张浩然

（南京信息工程大学a.总务处；b.教务处；c.电子与信息工程学院，南京210044）

0 引 言

自动调制识别（Automatic Modulation Recognition，AMR）是解调前的一项重要的技术，主要应用于军事中的电子战［1］和民用领域中的非法监管。AMR技术还可提高认知无线电［2］和软件无线电［3］中的频谱使用效率［4］。研究高效可靠的调制识别技术具有重要学术价值和工程实践意义。

AMR算法分为两类：一是基于决策理论的最大似然假设检验识别算法，包括广义似然比、平均似然比和混合似然识别算法［5］；二是基于特征提取的模式识别算法［6］。由于后者的计算量小，所需先验信息少，所以基于特征提取的模式识别算法被广泛研究，主要步骤有：数据预处理，特征提取和分类识别。常用的信号特征包括高阶累积量［7］、小波特征［8］和信号瞬时特征［9］等。分类识别算法有：支持向量机（Support Vector Machine，SVM）［10］，K最邻近（K Nearest Neighbor，KNN）［11］和朴素贝叶斯等［12］，这些算法需要进行提取专家特征的过程，且识别准确率较低。因深度学习算法在图像识别领域中表现出优势［13］，众多研究者将其引入各种模式识别的应用场景。深度学习算法中的卷积神经网络可以高效记忆和学习样本特征，并且对数据没有附加的特征提取要求，因此适合应用在调制信号的分类识别中。

利用卷积神经网络进行自动调制信号识别，主要的工作如下：为符合实际的信号传输环境，采用国际标准的调制信号数据集RaidoML2016.10a。将数据集中的信号IQ分量直接作为神经网络的输入，避免传统特征提取的计算步骤；设计两层卷积层的CNN，增加样本特征学习的多样性，减小由网络深度增加带来的特征退化。实验结果表明，本文设计的CNN的识别准确率优于对比的调制信号识别算法。

1 信号模型和累积量特征

1.1 调制信号模型

图1所示为典型的无线通信系统，其包括发射器、信道和接收器。接收器处的连续时间信号为

图1 无线通信系统组成

式中：x（t）为按照时间t发送的信号；f（t）为调制类型；符号“⊗”为卷积操作；h（t）为信道效应；n（t）为加性噪声。给定接收信号y（t），调制识别旨在预测f（t）的调制类型。

1.2 调制信号的累积量特征

对于一、二阶统计量，通常不能用于处理非线性、非高斯性或非最小相位系统相关的信号处理问题。而高阶统计量通常被用于解决这些类型的信号处理问题，对比的特征提取算法使用高阶累积量作为样本特征。

令y（n）表示在时间n处的离散时间接收信号，复数值接收信号y（n）的二阶统计量可以表示为：C20＝E［y2（n）］和C21＝E［｜y（n）｜n］，其中E（·）是期望函数。本文使用的特征为y（n）的四阶统计量。复数值信号y（n）的四阶统计量为

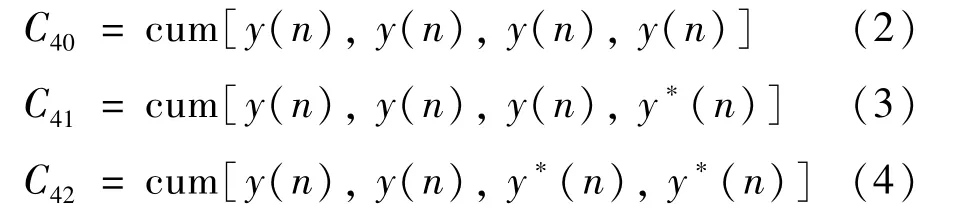
式中，C40、C41和C42为四阶统计量。具体而言，四阶统计量的联合累积量函数表示为

2 基于卷积神经网络的调制信号识别

2.1 基于CNN的调制信号识别

在使用CNN模型［14-17］进行调制识别时，由于CNN具有空间特征学习能力，可直接对调制信号的IQ分量进行处理，本节将信号的原始样本作为网络的输入。信号样本采用国际标准数据集RML2016.10a＿dict［19］。样本χ由信号的同相和正交分量组成。由于样本维度较小，本文设计的CNN不采用池化层来进行特征的降维，具体的网络结构和部分参数如图2所示。

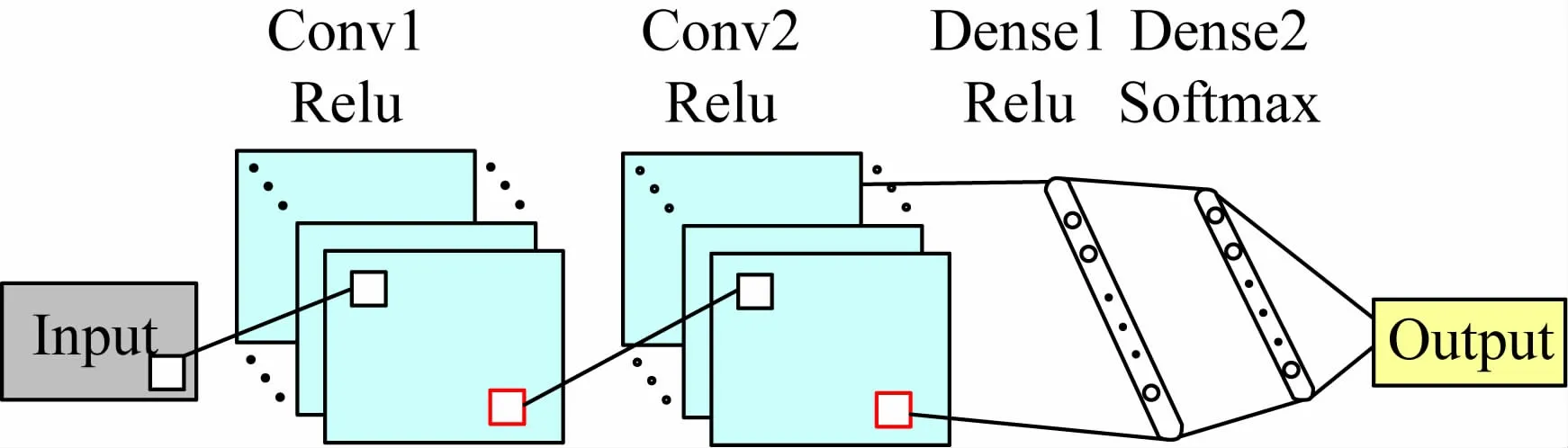
图2 基于CNN的调制识别模型

输入层Input，输入的样本大小为2×128。输入样本采取补零操作，即在样本两侧补上零矩阵，以保证样本的边缘特征能够被学习到。网络第2层为Conv1，卷积核个数为256，对应输出特征图通道数也为256。此外，本层卷积核尺寸为1×3，滑动步长为1。激活函数设置为Relu，为更好满足非线性需求，同时防止训练陷入局部最小。本层的输出x1计算式为

式中：xiq为补零后的IQ分量样本；σ（·）为Relu函数；W1、b1分别为第1层卷积层里的权重和偏置。

网络的第3层为Conv2，该层卷积核个数为128，卷积核尺寸为2×3，其余设置同卷积层1。这里增大了卷积核的尺寸，是为了学习二维信号特征的关联性，减少冗余特征，本层输出的特征图尺寸较上一层卷积层的1输出会有所减小。本层的输出为

网络的最后两层为全连接层，第1层全连接层的神经元个数为256，它接收上层输出的特征。在此之前，需对Conv2输出的特征图进行压平操作得到x′2，即将二维的特征压平为一维。本全连接层的激活函数也为Relu，输出的特征尺寸大小为1×256。其输出的计算过程为

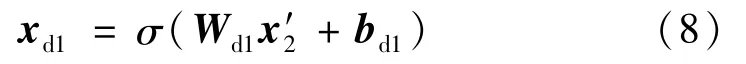
式中：x′2为x2被拉平后的一维特征；Wd1和bd1分别为第1层全连接层里的权重和偏置。

网络最后的全连接层也为输出层，激活函数为Softmax，以满足多分类的目的，神经元个数与分类的类别数相同，这里为信号的类别数11。此处的输出预测标签为

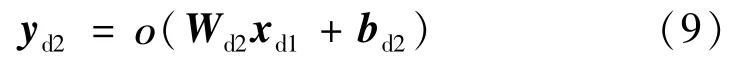
式中，ο（·）为Softmax函数。此外，设置网络中前3层特征提取层的dropout系数为0.5，即同一时刻，只有一半神经元处在激活状态，防止网络训练时发生过拟合现象。

2.2 CNN中激活函数的选择

Relu函数是当前人工神经网络中常用的激活函数，它在一定程度上缓解了梯度问题，计算速度非常快。Relu被使用在卷积层和全连接层，可加快模型的收敛速度，提高神经网络的训练性能。

网络输出层的激活函数为Softmax，也称为归一化指数函数。它是深度学习中非常普遍且重要的一种函数。Softmax常用于多分类过程，将多个神经元的输出映射到（0，1）间隔中，并将其理解为计算多分类的概率。其工作原理可解释为某种类型的特征加权，将这些特征转换为确定这种类型的可能性。涉及信号分类识别问题，在CNN中，最后一层全连接层使用Softmax激活函数进行分类识别，最终输出的是每个信号的概率。

2.3 识别准确率评价指标

准确率计算公式为

式中：n为样本数；＾yi为第i个样本的预测标签；yi为第i个样本的真实标签。

3 实验与分析

3.1 数据集

实验中，使用了RadioML2016.10a数据集作为输入数据，该数据集是目前调制识别研究中常被使用的数据样本，有关生成此数据集的详细信息可以在文献［19］中找到。该数据集包含11种调制信号类型，为8种数字调制和3种模拟调制，它们为BPSK、QPSK、8PSK、16QAM、64QAM、BFSK、CPFSK和4PAM数字调制信号，以及WBFM、AM-DSB和AM-SSB 3种模拟调制信号。该数据集是利用开源软件无线电平台GNU Radio生成，在产生过程中除了采用了大量真实语音信号，采用了GNU Radio中动态信道模型模拟信道效应，包括频率偏、相位偏、高斯白噪声和频率选择性衰落等。具体数据集的参数见表1。

表1 RaidoML2016.10a数据集的相关参数

3.2 CNN的识别准确率

实验中，将数据集220 000个样本划分为训练集和测试集，各占样本总量的80%和20%。实验使用tensorflow作为后端，使用keras库搭建神经网络训练，并基于Nvidia GEFORCE GTX1050Ti图形处理器进行神经网络的计算。使用的优化算法为Adam［20］，Adam优化算法是改进的随机梯度下降算法，是Momentum算法和RMSprop算法的结合体。网络的损失函数设置为交叉熵损失函数，它刻画的是网络输出概率与实际输出概率的距离，即交叉熵越小，两者概率分布越接近。在实验环境配置完毕后，将样本输入设置好参数的两种网络中，先后进行训练与测试，分别得到识别结果。CNN的识别准确率随信噪比的变化，如图3所示。

可见，CNN算法的识别准确率均随着信噪比的增加而逐渐增高。在信噪比为－20～－14 dB时，算法的识别准确率在10%左右。当信噪比高于－4 dB时，CNN的准确率开始高于60%。当信噪比为－2 dB时，CNN的识别准确率约为70%。当信噪比在6～18 dB时，CNN的识别准确率都趋于平缓。当信噪比为18 dB时，CNN的识别准确率为78.5%。

3.3 不同算法的对比

将CNN与两种特征提取的调制识别算法进行对比。特征提取的调制识别算法使用的信号专家特征为1.2节中提到的四阶累积量特征。对比的是SVM和KNN两种算法，准确率对比如图3所示。

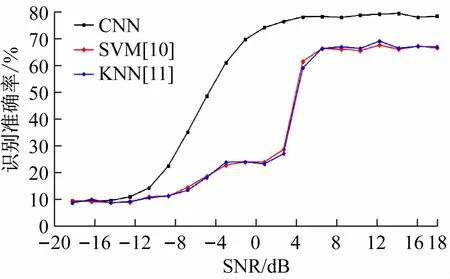
图3 CNN与SVM、KNN的识别准确率对比

可见，在信噪比为－20～－16 dB时，CNN、SVM以及KNN算法的识别准确率均在10%左右。随着信噪比的增加，3种算法的识别准确率均呈现增高的趋势。其中，CNN的识别准确率增长最快。在信噪比为0 dB时，CNN的识别率值则最高，为75%，而SVM和KNN的识别准确率低于25%。在信噪比为2 dB时，SVM和KNN的识别准确率呈现陡然上升趋势。当信噪比增加至4 dB之后，3种算法的识别准确率均趋于平缓状态，CNN比SVM的准确率高出约17%，比KNN的准确率高出约20%。在信噪比为18 dB时，CNN的识别率为78.5%，SVM为66.6%，KNN为67.0%。可见，特征提取的调制识别算法几乎在所有信噪比下识别准确率都低于卷积神经网络。说明，卷积神经网络的调制识别算法不仅可以避免特征提取的计算步骤，还取得优异的识别性能。

3.4 CNN识别结果的混淆矩阵

针对RML2016.10a数据集中多种调制类型，进一步研究CNN的识别性能，利用混淆矩阵来观察每个类型的识别情况。混淆矩阵的横坐标为样本的网络预测信号类型（预测标签），纵坐标为这些样本的实际信号类型（真实标签）。图4为CNN在信噪比为－18 dB时的识别结果混淆矩阵。

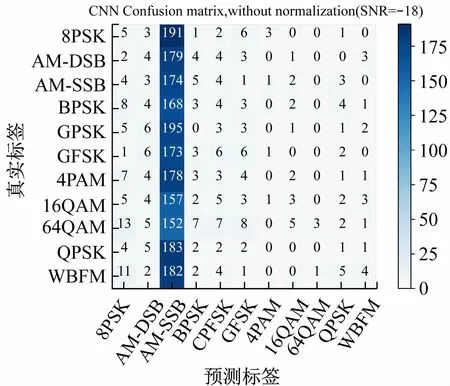
图4 在信噪比为－18 dB时CNN的混淆矩阵

在混淆矩阵的网格中，每格中的数字表示样本数量。以图4为例，对于纵坐标为8PSK的这一行数据，对应到横坐标可见：网络将8PSK正确预测为8PSK的样本数量只有5个，而将8PSK预测为AM-SSB的样本数量为191个，出现了严重的混淆。说明由于低信噪比的影响，CNN的识别准确率较差，对任意种类的信号都难以识别。

图5为CNN在信噪比为0 dB时的识别结果混淆矩阵。图5表明，CNN对大部分信号类型都能进行准确识别，而对于AM-DSB和WBFM，16QAM和64QAM的识别效果较差。因为生成数据集时，观测窗口小，信息率低，信息之间关联性小，所以难以区分AM-DSB和WBFM。而对于16QAM和64QAM，这两种信号的IQ信息相似，也难以进行分类识别。另外，在0dB情况，QPSK和8PSK两种信号也有较少的混淆。

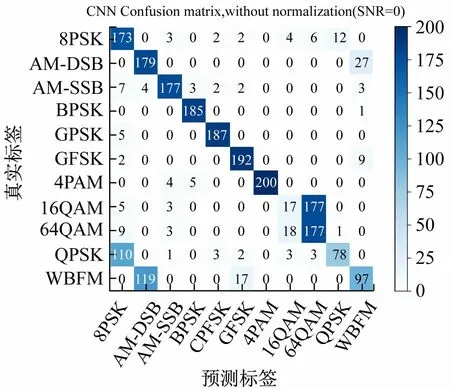
图5 在信噪比为0 dB时CNN的混淆矩阵

图6为CNN在信噪比为18 dB时的识别结果混淆矩阵。图6表明，在信噪比为18 dB时，CNN对BPSK信号的识别准确率较0 dB时有少许的提高，对于AM-DSB和WBFM，16QAM和64QAM的识别，CNN表现的效果仍然较差，而对于其他类型信号，CNN取得了较好的识别性能。

图6 在信噪比为18 dB时CNN的混淆矩阵

4 结 语

针对基于特征提取的调制信号识别算法准确率不高的问题，本文采用卷积神经网络（CNN）用于调制信号的识别。卷积神经网络可以直接对二维样本进行特征学习，避免专家特征计算过程，直接将调制信号的IQ分量作为网络输入。利用卷积层提取空间特征，还能学习到样本的时序特征。本文采用国际标准数据集，其中的信号受多种信道效应影响，接近真实通信环境。仿真结果表明，在信噪比大于－16 dB情况下，CNN的调制信号识别准确率远远高于SVM和KNN，说明基于卷积神经网络的调制识别算法不仅可以避免人工提取专家特征，而且在性能上也有很大的优势。