一种模拟介质交界面处达西流速的分区多尺度有限单元法

谢一凡，吴吉春，叶 逾，谢春红，鲁春辉，5

（1.河海大学 水文水资源与水利工程科学国家重点实验室，江苏 南京 210098；2.河海大学 水利水电学院，江苏 南京 210098；3.南京大学 地球科学与工程学院，江苏 南京 210023；4.南京大学 数学系，江苏 南京 210093；5.河海大学 长江保护与绿色发展研究院，江苏 南京 210098）

1 研究背景

天然地下水系统常由多种不同的含水介质组成，伴随着裂隙、透镜体等地质特征。在含水介质交界面处，根据折射定律，交界面法向达西流速和水头具有连续性，切向达西流速则具有不连续性且需按折射定律呈比例［1-3］。然而，有限元等传统方法难以保证达西流速的连续性，更不能保证交界面处的达西流速符合折射定律。另一方面，地下水问题具有时空大尺度特性、非均质性等特征。有限元法在模拟地下水问题时常需要精细剖分的网格以保证精度，而精细剖分的网格中含有大量的节点，需要大量的计算消耗和计算时间进行模拟，导致有限元等传统方法在模拟地下水问题时的计算效率较低［4-5］。本文提出的分区多尺度有限元法（MSFEM-D）能够有效解决上述问题，不仅能够令交界面处的达西流速满足折射定律，并且具有极高的计算效率。

连续达西流速算法能够保证节点达西流速值唯一，即流入流出某截面的流量守恒，具有重要意义。然而，有限元等传统算法无法保证节点水力梯度连续性，也无法获得连续的节点达西流速。现有连续达西流速算法具有比传统有限元等方法更高的精度，主要有两种模拟方式。第一种是将水流方程和达西方程进行耦合，将水头和达西流速同时作为未知项，迭代求解达西流速。这种方式具有较高的计算精度，但需要较大的计算消耗来进行迭代，代表方法为混合有限元法［6-7］。第二种则是将水头和达西流速先后分别通过水流方程和达西方程进行模拟。这种方式的算法简单直接，也具有较高的计算精度，应用比较广泛，代表方法有Yeh的伽辽金有限元模型［8］、张志辉等的三次样条法［9］、Batu的双重网格法［10］等。其中，Yeh的伽辽金有限元模型应用最广泛，还可保证全局质量守恒［11］。

虽然Yeh在传统有限元基础上改进了模型［8］，能保证节点达西流速的连续性，却无法保证折射定律对切向达西流速部分的要求，即无法保证交界面两侧的切向达西流速按照折射定律呈比例［12］。科学工作者为此提出了间断有限元法［13］、改进的Yeh的S1有限元模型［3］等交界面处理技术。其中，Zhou等改进Yeh的模型提出的S1有限元模型具有较高的精度，并且原理十分简单，适用于多种形态的交界面［3］。该模型通过折射定律构造了一种Jump函数，并运用其改进了Yeh的模型中交界面节点部分的方程，从而通过迭代修正达西流速至交界面某一侧的真实达西流速，再通过折射定律得到交界面另一侧的达西流速；但因其运用Jump函数时需要迭代，需要比Yeh的模型更大的计算消耗［3］。

另一方面，上述多种达西流速算法均受到有限元算法框架的限制，在模拟大尺度、非均质地下水问题时效率较低。对此，侯一钊等提出多尺度有限元法（MSFEM）［14］是一种有效对策，它能够通过构造满足局部水流方程的多尺度基函数来描述细尺度信息，从而将细尺度问题转化为粗尺度问题来大幅降低计算消耗，具有比有限元等传统方法更高的计算效率［4，14-15］。近年来，该方法不断被国内外科学工作者改进，提出了多种新型地下水多尺度算法［16-19］，并成功应用于地面沉降等实际问题［20］，显示该方法在地下水数值模拟领域的应用前景。作者也将多尺度有限元法与上述第二种方式算法中的三次样条法、双重网格法结合，提出了多种高效达西流速算法［21-23］，取得了较好的模拟结果。

本文提出的MSFEM-D属于第二种方式的达西流速算法，可以有效解决上述问题。MSFEM-D不仅能够令交界面处的达西流速满足物理规律，且具有下面两方面优势：（1）该方法不仅能够通过Yeh的伽辽金有限元模型［8］保证达西流速的连续性，而且能够通过区域分解技术将研究区用交界面分区，避免不同介质在模拟时的相互影响并提升计算效率，同时结合Jump函数［3］保证交界面达西流速符合折射定律，且无需任何迭代过程。（2）该方法通过多尺度有限元框架［14］替代有限元框架，能够提升水头和达西流速的问题尺度，将大量细尺度节点替换为少量的粗尺度节点，从而降低解水头和达西流速计算消耗，具有极高的计算效率。

2 原理和算法

2.1 MSFEM-D的算法流程 MSFEM-D算法适用于地下水二维问题，算法流程图如图1。MSFEMD算法分为两个部分，即水流问题模拟部分（图1左上虚线框部分）和达西流速模拟部分（图1右侧）。

图1 MSFEM-D算法流程

MSFEM-D 的地下水流问题模拟部分采用现有的MSFEM 算法［14］模拟水头，通过构造多尺度网格和多尺度基函数可以显著提升计算效率并保证精度。MSFEM-D的达西流速模拟部分为本文的主要创新部分，该部分综合了区域分解算法、MSFEM［14］、Yeh的伽辽金有限元模型［8］和Zhou根据折射定律构造的Jump函数［3］的优点。首先，MSFEM-D运用交界面将研究区剖分为子区域，并运用区域分解算法将研究区上的模拟问题划分为若干子区域上的子问题。其次，MSFEM-D 将MSFEM 和Yeh 的伽辽金有限元模型进行了组合，即，运用MSFEM的多尺度基函数替换Yeh的伽辽金有限元模型中的有限元基函数。再次，运用MSFEM和Yeh的伽辽金有限元模型的组合方法求解子区域上的子问题；在获得首个子问题上交界面处的达西流速值后，通过折射定律构造的Jump函数获得其相邻子区域交界面上的达西流速，并作为下一个子问题的边界条件。最后，循环这个过程，直到求解完毕。需要指出的是，在实际工作中，需要根据实际地下水问题的条件进行建立概念模型、选择数学模型，再应用本算法，并进行模型校正等后续步骤以完成地下水问题的模拟工作。

2.2 MSFEM-D的网格构造 设水平方向为x方向，垂直方向为y方向。图2为MSFEM-D对含一条水平交界面的示例研究区Ω的剖分，具体分为水头模拟网格和达西流速模拟网格两部分。

2.2.1 MSFEM-D 的水头模拟网格 在模拟水头时，MSFEM-D 运用多尺度网格进行剖分［14］，先将研究区剖分为粗网格，再将粗网格剖分为细网格。本方法的粗、细网格的数量可以根据数值模拟具体需要进行设置。图2为本文的数值模拟实验所用的剖分，MSFEM-D先将Ω直接剖分为1800（30×30×2）个三角形粗网格单元，此时交界面AB不作为分区界限。然后，MSFEM-D 再将每个粗网格单元剖分为9（3×3）个细网格单元，图2右侧小三角形Δijk为一示例粗网格单元及其细网格单元。

2.2.2 MSFEM-D的达西流速模拟网格 在模拟达西流速时，MSFEM-D先运用交界面将研究区剖分为若干个仅含单一介质子区域，再进行粗、细网格剖分，具体粗、细网格的数量可根据数值模拟的需要进行设置。如图2中，MSFEM-D运用AB将研究区剖分为Zone 1和Zone 2两个子区域，然后延用水头的模拟网格分别将两个子区域剖分为900（30×15×2）个粗网格单元，再将每个粗网格单元剖分为9个细网格单元。

图2 MSFEM-D对示例研究区的剖分

2.3 折射定律与Jump函数 在含水介质交界面处，地下水水头和达西流速需符合折射定律［1-2］：

式中：V为达西流速向量；n为交界面的法向单位向量；H为水头；+、-号分别代表交界面的两侧。

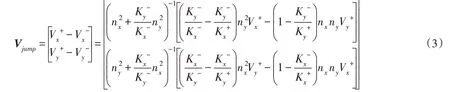
2.4 构造多尺度基函数 设示例粗网格单元为Δijk，其顶点i、j、k的多尺度基函数分别为Ψi、Ψj、Ψk，Δijk具有p个内点，Mτ，τ=1，2，…，p。以多尺度基函数Ψi的构造过程为例，考虑在粗网格单元Δijk上的简化的椭圆方程：

在设定多尺度基函数的边界条件后［14］，式（4）适定。

在粗网格单元Δijk中的任意细网格单元Δabc内，Ψi可被线性表示为［14］：

式中：Na、Nb、Nc为有限元线性基函数；Ψi(a)、Ψi(b)、Ψi(c)为Δabc顶点处的Ψi的值。对式（4）进行伽辽金变换，再将式（5）代入，可以得到关于Ψi的方程组，求解可得Ψi在Δijk中所有节点的值。其他多尺度基函数的构造过程与Ψi类似，这里不再赘述。

2.5 运用MSFEM-D模拟二维地下水问题

2.5.1 运用MSFEM-D模拟地下水水头 以地下水二维非稳定流问题为例，考虑如下方程：

式中：W为源汇项；Ω为研究区；S为贮水系数。在地下水模拟问题的定解条件确定后，式（6）适定。

在水头模拟时，无需运用交界面进行分区，可以直接剖分研究区。在式（6）两边乘以多尺度基函数Ψi，进行伽辽金变换，再离散到每一粗网格单元Δijk上，可得：

根据文献［14］，在粗网格单元Δijk上，Ψi可被线性表示为：

式中Hi、Hj、Hk分别为水头H在粗网格单元Δijk顶点i、j、k处的值。

将式（7）离散到细网格上，并代入式（5）、式（8）可得式（7）的具体表达式。再运用Ψj、Ψk乘以式（6）两端，并重复上述过程，可得粗网格Δijk上关于水头H的单元刚度矩阵。联立所有粗网格上的单元刚度矩阵，结合源汇项W、初始条件、边界条件即可得到右端项，从而得到研究区上的总方程组，结合Cholesky分解法等矩阵求解方法即可获得研究区上的水头在研究区粗尺度节点上的值。

2.5.2 运用MSFEM-D模拟达西流速 在获得研究区的水头分布后，MSFEM-D可以运用这些已知的水头值，结合区域分解技术、MSFEM［14］、Yeh的伽辽金有限元法［8］以及Zhou的Jump函数［3］进行达西流速的求解。其中，水头值可以提供研究区的全局信息，区域分解技术可以分离介质避免互相影响、MSFEM基函数可以提高模拟效率、Yeh的伽辽金法可以保证达西流速的连续性。以Vx的求解过程为例，在图2所示的研究区Ω上考虑达西方程：

如2.2.2 节所述，MSFEM-D 已经将研究区Ω划分为Zone 1、Zone 2 两个子区域。MSFEM-D 运用区域分解技术将研究区上的达西流速求解问题划分为Zone 1、Zone 2这两个子区域的子问题。设先求解Zone 1上的子问题，则需在Zone 1上考虑式（9）。设子区域Zone 1上的粗尺度网格数目为γ1，粗尺度节点数目为Nu1，运用ΨI，I=1，2，…，Nu1乘以达西方程的两端，并在Zone1 上积分，并将Zone 1离散为γ1个粗网格Δijk，可得：

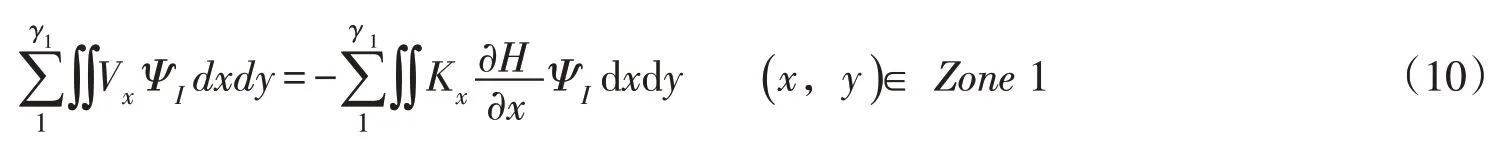
在任意粗网格Δijk上，根据现有文献中的理论［8，14］，Vx可以被多尺度基函数线性表示为：

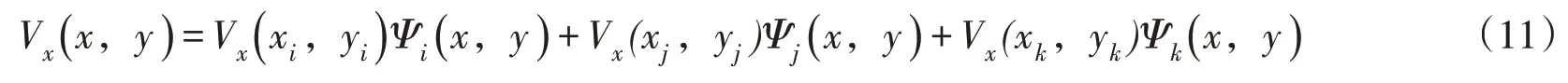
式中Vx(xi，yi)、Vx(xj，yj)、Vx(xk，yk)为达西流速Vx在粗网格Δijk顶点i、j、k上的值。

将式（11）代入式（10）左端，将式（8）代入式（10）右端，可得：

将式（12）、式（13）结合式（5），可得Zone 1上关于达西流速Vx的方程组的具体形式，求解可以获得Zone 1 区域上的Vx值，其中包括了在Zone 1 的边界上，即在Zone 1 一侧的介质交界面AB上的Vx值。结合Jump函数式（3），即可获Zone 2一侧的介质交界面AB上的Vx值，这将作为Zone 2上的子问题的第一类边界条件。在Zone 2上，运用类似上述达西流速的模拟过程，即可获得Zone 2区域的粗尺度Vx值。在所有子问题求解完毕后，可以得到Ω上的Vx值。在Ω进行类似上述Vx的达西流速的模拟过程，即可以得到Ω上的粗尺度Vy值。

上述过程中，MSFEM-D运用了多尺度基函数模拟地下水流和达西流速，得到了水头和达西流速的粗尺度网格上的解。因而，MSFEM-D的水头和达西流速的总方程组的阶数均远低于精细剖分的传统方法，具其有极高的计算效率。

3 数值模拟实验

采用如下缩写方式：Vx表示x方向上的达西流速；Vy表示y方向上的达西流速；FEM-F表示精细剖分的有限元法；Model-Yeh-F 表示精细剖分的Yeh的伽辽金有限元模型；Model-Zhou-F 表示精细剖分的Zhou等的S1有限元模型；MSFEM-D表示多尺度有限元与区域分解法的组合方法。

本节模拟了含水平介质交界面的渗透系数非均质各向异性的地下水二维稳定流问题以及含水平与倾斜两个介质交界面的地下水稳定流问题的水头和达西流速，并将MSFEM-D 所模拟的水头与FEM-F比较，MSFEM-D所模拟的达西流速与Model-Yeh-F［8］以及Model-Zhou-F［3］两种现有达西流速算法进行比较。为了比较计算消耗与精度，FEM-F、Model-Yeh-F、Model-Zhou-F 的网格数目均等于MSFEM-D的细网格数目，且所有数值方法均采用了线性基函数的边界条件。同时，所有数值方法均采用C++编写，均采用Cholesky 分解法求解总方程的矩阵，没有应用并行计算技术。在测量CPU时间时，各方法均在同一计算机上独立运行。

3.1 含水平交界面的渗透系数非均质各向异性的二维地下水稳定流问题 本例基于Cainelli等在2012年工作［4］中的数值算例所设置，具有解析解。本例的地下水水流和达西流速的控制方程分别为，二维地下水稳定流方程和达西方程（式（9））。研究区域Ω为［0，1］×［0，1］。研究区内含有两种不同的各向同性含水介质（图2），分别位于Zone 1和Zone 2两个区域，它们的交界面为AB（y=0.5）。渗透系数呈非均质各向异性变化，Zone 1、Zone 2的渗透系数分别为：K1x=（1+x）（1+y），K1y=10（1+x）（1+y）和K2x=10（1+x）（1+y），K2y=100（1+x）（1+y）。本例中，地下水水流方程中的源汇项W和研究区的边界的第一类边界条件由如下水头H的解析解给出：

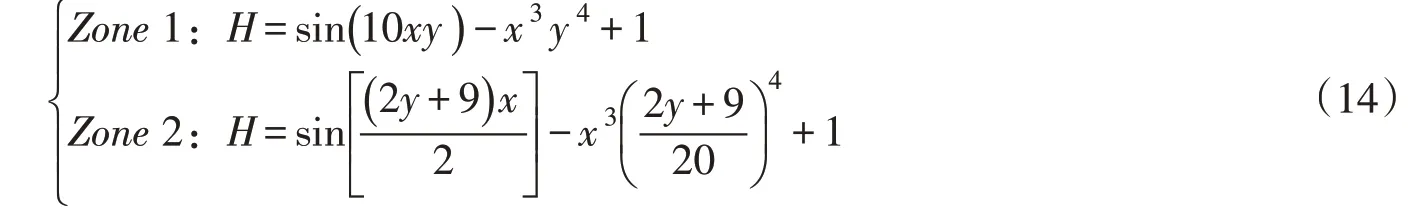
此外，x方向上的达西流速Vx的解析解为：

y方向上的达西流速Vy的解析解为：

本例中，MSFEM-D先将研究区剖分为1800（30×30×2）个三角形粗网格单元，再将每个粗网格剖分为9（3×3）个三角形细网格单元，即总计16 200个细网格单元；Model-Zhou-F、Model-Yeh-F 直接将研究区剖分16 200（90×90×2）个网格单元。

如前所述，MSFEM-D 应用MSFEM 直接在研究区内计算全局水头，而Model-Zhou-F、Model-Yeh-F 均使用FEM-F 进行全局水头模拟，FEM-F 的网格剖分与Model-Zhou-F、Model-Yeh-F 一致。MSFEM-D和FEM-F在本例都能获得很高的水头计算精度，全局平均误差分别为0.079%和0.024%。

图3展示了解析解Vx以及各方法的数值解Vx在交界面AB（图3（a））以及截面x=0.5 m处（图3（b））的值。从图3（a）中可以看出，MSFEM-D与Model-Zhou-F所获的数值解以及解析解在AB两侧均具有两个不同的值。这是由于水流在交界面产了折射，引起AB的切向达西流速Vx在交界面上不连续。MS⁃FEM-D、Model-Zhou-F 的曲线与解析解重合，显示这两个方法均具有较高的精度并符合折射定律，并且多尺度网格和精细剖分的网格都可以较有效的处理非均质渗透系数。另一方面，Model-Yeh-F在交界面两侧的值相等，且位于解析解两侧值中间的位置，具有较大的误差。这是由于Model-Yeh-F在求解达西方程时，没有对交界面进行处理，因而其得到的解为交界面两侧达西流速的平均值，不符合折射定律。因此，Model-Yeh-F与其他方法在交界面处的误差值具有较大的差异，以Zone 2侧的达西流速结果为例：MSFEM-D、Model-Zhou-F 的相对误差值分别为0.52%和0.15%；Model-Yeh-F对于Zone 2侧的解析解的误差为45%。此外，由于Zone 1侧的解析解绝对值较小，Model-Yeh-F的对于Zone 1的解析解的相对误差甚至达到了100%。从图3（b）中可以看出，在交界面附近节点上Model-Yeh-F 的解出现了振荡，这是由于Model-Yeh-F 在交界面附近节点上的解需要“补偿”其在点（0.5，0.5）的解的误差。由于MSFEM-D、Model-Zhou-F对交界面进行了处理，它们的解在交界面附近依然保持了高精度，和解析解重合。在远离交界面AB的位置，Model-Yeh-F 可以表现的很好，精度与MSFEM-D、Model-Zhou-F相近，故图中三个方法均与解析解重合。事实上，Model-Yeh-F在远离交界面处的值与Model-Zhou-F完全一致，这是因为Model-Zhou-F仅对交界面处的达西流速的相关方程进行了修正。

图3 达西流速Vx的解析解和MSFEM-D、Model-Zhou-F和Model-Yeh-F所获的数值解

图4展示了解析解Vy以及各方法所模拟的数值解Vy在研究区Ω上的分布。由于Vy在交界面AB上连续，MSFEM-D 可以直接运用水头网格在研究区Ω上求解，Model-Zhou-F 无需运用Jump函数进行修正，因而Model-Zhou-F和Model-Yeh-F所获的Vy场完全相同。如图4所示，虽然y方向的渗透系数在Zone 1、2 内不同，但解析解和各方法的数值解Vy在交界面AB处均连续，这符合折射定律。同时，MSFEM-D 和Model-Zhou-F 所获的数值解与解析解很接近，两种方法的全局平均相对误差均分别为1.1%和0.2%。这是由于Model-Zhou-F是直接在细尺度上求解方程的，能够获得比MSFEM类方法略高的计算精度，但这也产生了大量的计算消耗，降低了其的计算效率。

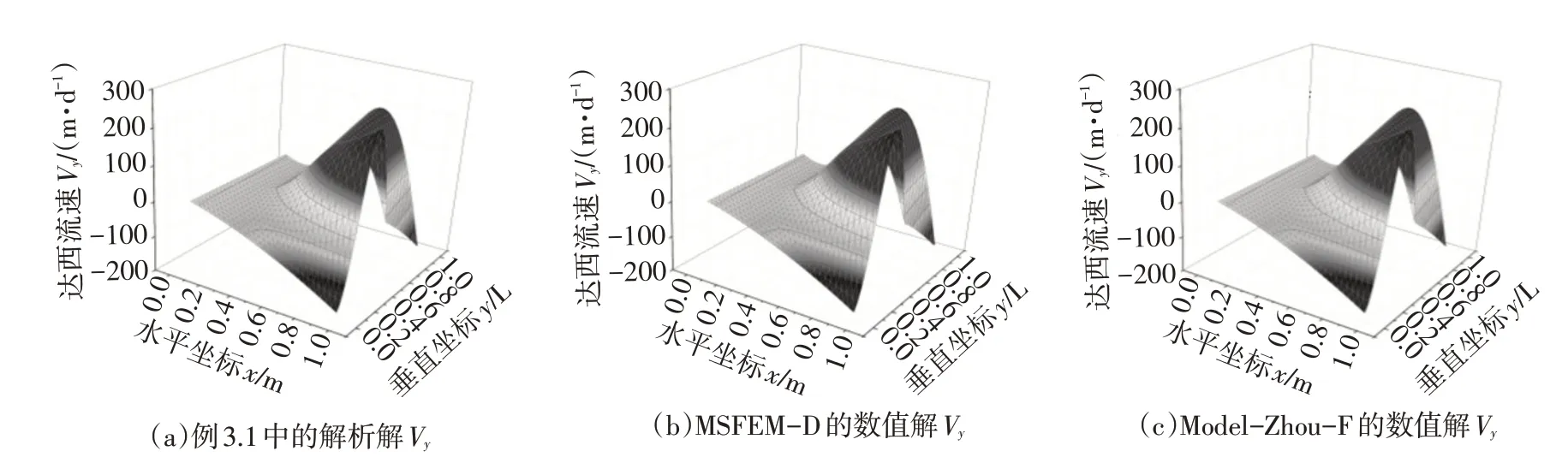
图4 达西流速Vy的解析解以及MSFEM-D和Model-Zhou-F所获的数值解

本例中各方法的计算消耗对比如表1 所示。其中，Model-Zhou-F 所消耗的4236 s 的CPU 时间中，204 s为运用FEM-F模拟水头的时间；3789 s为模拟Vx场的时间，因处理交界面而迭代了15次；243 s为模拟Vy场的时间，因Vy在交界面连续而无需迭代。Model-Yeh-F则使用了204 s模拟水头，并分别运用两个243 s模拟Vx场和Vy场。和其他方法不同，MSFEM-D 所构造的模拟水头、达西流速的方程组的阶数都很低，故MSFEM-D仅使用不到1 s即可完成本例的模拟，且能获得与Model-Zhou-F几乎相同的效果，具有最高的计算效率。

表1 例3.1中各方法的计算消耗对比

3.2 含水平与倾斜两个介质交界面的二维地下水稳定流问题 本例是基于Zhou等在2001年工作中的数值算例［3］。本例的地下水水流和达西流速的控制方程与上例相同。研究区域Ω为［0，120 m］×［0，120 m］。如图5所示，研究区所含的两条交界面为水平交界面AB（y=20 m）和倾斜交界面CD（x+y=160 m）。这两条交界面将研究区分为Zone 1、Zone 2、Zone 3 三个区域，相应的渗透系数分别为Kx=Ky=100 m/d、K2x=K2y=10 m/d 和K3x=K3y=100 m/d。研究区上下边界为隔水边界，左右边界为定水头边界，左右水头值分别为0 m和1 m。

本例采用MSFEM-D、Model-Zhou-F 和Model-Yeh-F 进行模拟。MSFEM-D 将研究区剖分为1152（24×24×2）个粗网格单元，再将每个粗网格单元剖分为4个细网格单元（图5右侧）；MSFEM-D在模拟达西流速时，在每个子区域中延用了水头网格；Model-Zhou-F、Model-Yeh-F 直接将研究区剖分4608（48×48×2）个网格单元。本例没有解析解，故将运用Model-Zhou-F 将研究区剖分为18 432（96×96×2）个单元获得的解作为“参照解”。

图5 例3.2中的研究区Ω示意图

各方法所获的水头值如图6所示。可以看出，研究区的水头场是按照图6所示的区域进行分布的，能够较明显的看到研究区内所包含的交界面。MSFEM-D运用MSFEM所获的水头场以及Model-Zhou-F和Model-Yeh-F运用FEM-F所获的水头场的精度都很高，水头平均相对误差分别为0.58%和0.15%。

图6 水头参照解以及MSFEM-D和FEM-F所获的数值解水头

图7 展示了参照解以及各方法的数值解Vx在交界面AB（图7（a））以及截面x=80 m 处（图7（b））的值。从图7（a）中可以看出，MSFEM-D 和Model-Zhou-F 能够满足折射定律，并与参照解重合，它们在交界面AB的Zone 1侧的平均相对误差分别为0.016%和0.007%。Model-Yeh-F在交界面处依然无法满足折射定律，具有较大的误差，其对Zone 1 侧解析解的误差为45%。从图7（b）中可以看出，MS⁃FEM-D和Model-Zhou-F在交界面附近依然可以取得精确的解，而Model-Yeh-F在AB、CD两个交界面附近均出现了“补偿”现象，具有较大的误差。在远离交界面处，三种方法均和参照解重合，具有较高精度。

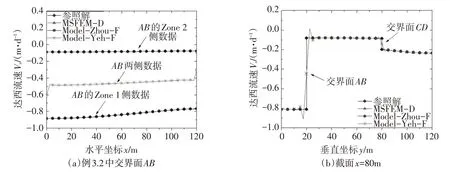
图7 达西流速Vx的参照解以及MSFEM-D和Model-Zhou-F所获的数值解

图8展示了交界面CD处达西流速Vx（图8（a））和Vy（图8（b））的参照解和MSFEM-D、Model-Zhou-F和Model-Yeh-F所获的数值解。如图8所示，CD为倾斜交界面，不平行于任何坐标轴，故达西流速Vx和Vy均在CD上不连续，具有两个不同的值。本图中，MSFEM-D、Model-Zhou-F 能够满足折射定律，且均能接近参照解，它们在Zone 2侧的Vx的平均相对误差分别为7.3%和1.6%（图8（a））。和上例相比，两种方法在交界面处的误差均有增长，这是由于Vx在边界处变化较快而引起的，可以通过加密网格提高精度。由于Model-Zhou-F是直接在全局细尺度网格（48×48×2）上进行达西流速求解，而MS⁃FEM-D则是在（24×24×2）的粗尺度网格上进行达西流速求解；Model-Zhou-F能够获得高于MSFEM-D的精度，但所需消耗也远大于MSFEM-D，为其的200倍以上。Model-Yeh-F 无法满足折射定律，在交界面CD处具有较大的误差，其对Zone 2侧Vx参照解的平均相对误差为28.3%（图8（a））。

图8 达西流速Vx和Vy的参照解以及MSFEM-D、Model-Zhou-F和Model-Yeh-F所获的数值解

在本例中，MSFEM-D 仅消耗不到1 s 的CPU 时间即可完成粗、细尺度的水头和达西流速的模拟，且精度接近Model-Zhou-F；而Model-Zhou-F 则需要迭代14次，共需要207 s才能完成相同的工作；Model-Yeh-F虽然仅需要18 s CPU时间，但其无法保证达西流速在交界面上符合折射定律。这一结果显示，MSFEM-D具有较高的计算效率，并能适用于倾斜交界面和多条交界面的情况。

4 结论与展望

本文提出分区多尺度有限元法（MSFEM-D）用于模拟交界面处的地下水达西流速。在构造水流和达西流速方程时，该方法以MSFEM的框架为基础，进行了尺度提升，提高了计算效率。在模拟交界面达西流速时，该方法运用区域分解技术分离不同介质避免互相影响，并运用Yeh 的伽辽金模型保证达西流速的连续性，结合Jump函数，从而令交界面处的达西流速符合折射定律。

多种情形下含交界面的地下水数值模拟实验结果表明：（1）MSFEM-D 不仅能够在含单条、多条、水平、倾斜交界面的地下水问题中保证交界面处达西流速满足折射定律，还可以处理渗透系数为非均质各向异性的情况。（2）MSFEM-D 的全局水头精度与FEM-F 相近，全局达西流速的精度与Model-Zhou-F接近，其在交界面处的达西流速比Model-Yeh-F更加精确。（3）MSFEM-D无需任何迭代过程，其计算消耗低于Model-Yeh-F，更是远低于需要迭代的Model-Zhou-F，能够节约大量的计算成本。

在今后的工作中，将继续改进MSFEM-D，研究含交界面的三维地下水问题的模拟方法；结合钻孔和地质图等实际信息，提出交界面的描述方法，研究实际案例的模拟方法；开发MSFEM-D软件，并与现有的FEFLOW常用有限元软件进行对比。