适用于明渠流及冰盖流的统一泥沙颗粒起动流速公式

马子普，张宝森，邓 宇，李春江

（1.黄河水利委员会 黄河水利科学研究院，河南 郑州 450003；2.水利部堤防安全与病害防治工程技术研究中心，河南 郑州 450003；3.中国水利水电科学研究院 泥沙研究所，北京 100048；4.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024）

1 研究背景

高纬度地区河流在冬季常形成冰盖或冰塞，冰盖或冰塞的出现显著改变了水流的水力条件、热力条件及几何边界条件［1-2］，过水断面湿周和阻力明显增加，断面平均流速大幅减小［3］，产生了明显异于明渠流的特有泥沙输移现象［4］。冰盖流条件下，泥沙浓度及输移强度与明渠流相比很小［5-6］。

泥沙输移强度小，并不意味着泥沙颗粒在冰盖流条件下很难。以2014年冰期黄河头道拐断面套绘图（图1）为例［7］，该断面在1月4日至2月28日之间，发生强烈的冲淤变化。1月4日深泓点在540 m附近高程约983.68 m，1月19日深泓点则到了460 m 附近高程降低到982.44 m，1月22日则到了440 m附近高程降低到982.1 m，而560 m附近则大幅淤高2 m左右，1月28日深泓点仍在440 m附近，但高程继续降低到了981.65 m。该情形说明即使冰盖存在，但只要水动力较强，泥沙颗粒也可以起动，引起床面发生冲刷。

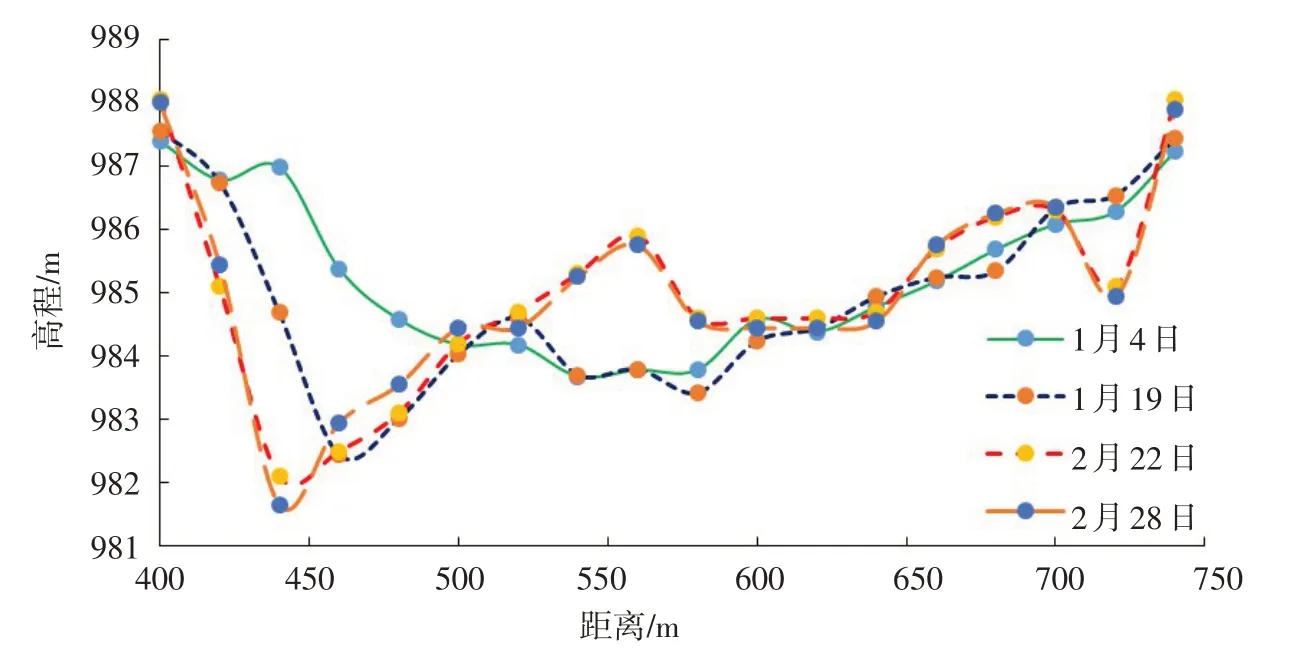
图1 头道拐水文断面2014年冰期不同时段河床断面套汇图

明渠流条件下的泥沙起动流速公式已有很多研究［8-11］，冰期泥沙颗粒的起动研究相对较少。王军和孙连进［3］通过水槽试验，研究了了冰盖流条件下的河床泥沙起动流速，认为冰盖下泥沙起动流速与冰盖及槽底糙率的相对比值有关。WANG［12］、SUI等［13］、WU等［14］建立了冰盖下散粒体泥沙颗粒起动的希尔兹曲线，并通过水槽实测资料进行了检验。本文将在探讨冰下泥沙颗粒起动的物理机制基础上，从Einstein假定出发，采用指数形式的流速分布公式，推导明渠流及冰盖流的非黏性泥沙颗粒起动流速公式，并将公式计算结果与已有实测资料进行对比以检验公式的合理性，应用所得公式对明渠流、冰盖流、冰塞条件下的起动流速及最大可起动粒径进行分析，进而从泥沙起动的角度分析了2014年黄河头道拐断面冰期强烈冲淤变化的原因。

2 冰下泥沙颗粒起动的物理机制

冰期河道床面上的泥沙颗粒同样也会发生大规模的运动。床面上泥沙颗粒的起动，主要取决于其综合受力情况，无论是明渠流还是冰盖流，床面上泥沙颗粒所受力的种类并无差别，对于非黏性的泥沙颗粒来说，主要受到水下有效重力、拖曳力及上举力作用［15-17］。水下有效重力属于泥沙颗粒本身的物理属性，拖曳力及上举力均与作用于泥沙颗粒上的流速即底部作用流速的平方成正比。无论是明渠流还是冰盖流，床面上同一粒径的泥沙颗粒要发生起动，需要达到的底部作用流速值是相同的。冰盖的存在，并不能改变泥沙颗粒起动所需的临界底部作用流速值的大小，若底部作用流速达不到，则泥沙颗粒就无法起动。

冰盖的存在，改变了整个垂线上的流速分布［18-21］，当以通常的垂线平均流速来表示起动流速时，同样的底部作用流速必然会对应不同的起动流速，基于此分析，对冰下床面泥沙颗粒的起动公式进行推导。

3 统一的泥沙颗粒起动流速公式推导

冰盖流条件下的垂线流速分布公式有对数、指数、双幂律、抛物线等多种形式［22-24］，这里采用如下的冰盖流指数流速分布公式进行推导：

式中：y为垂线上的点到床面的距离；u1(y)、u2(y)分别为冰盖区和床面区内垂线上点y处的水流流速；u1max、u2max为冰盖区和床面区的垂线最大流速；ℎ1、ℎ2分别为冰盖区、床面区的水深，ℎ 为冰盖流总的水深；m1、m2为冰盖区和床面区的垂线流速分布指数。

明渠流、冰盖流及冰塞示意图（图2）如下：

图2 明渠流、冰盖流、冰塞示意图

采用Einstein假定，将整个过流断面划分成上部冰盖区和下部床面区，以最大流速所在面作为上下两区的分界面，垂线流速分布满足三个条件［25］：（1）冰盖区的水流平均流速等于床面区的水流平均流速，即U1=U2=U；（2）河床水流与冰盖水流交界面的流速相等，等于垂线最大流速u1max=u2max=umax；（3）床面区水流与冰盖区水流的能坡相等J1=J2=J，且ℎ=ℎ1+ℎ2。

由式（1）可得：

而U1=U2=U，u1max=u2max=umax，则m1=m2。

式中：U1、U2分别为冰盖区及床面区的水流平均流速；U为冰盖流的水流平均流速；umax为垂线上最大流速；J1、J2分别为为冰盖区及床面区水流的能坡；J为冰盖下水流的能坡。

由此式（1）可化为：

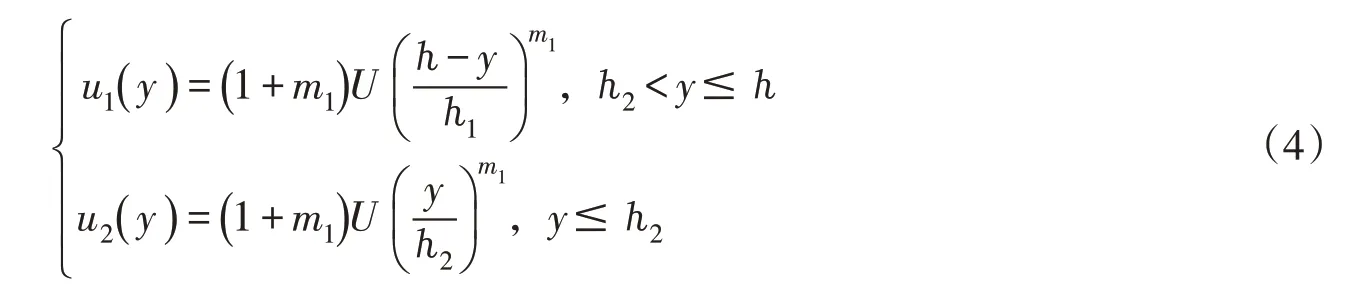
认为冰盖的厚度相对整个水深来说很小，ℎ ≈ ℎ0，则以指数流速分布形式表示的明渠流垂线流速分布公式：

式中：u(y)为明渠流垂线上点y处的水流流速；ℎ0为明渠流的水深；u0max为明渠流的水面流速；m为明渠流的垂线流速分布指数。

式（5）可化为：

式中U0为明渠流的垂线平均流速。

假定作用点位置为αD，当底部作用流速为ubc时，泥沙颗粒开始起动，那么：

对于冰盖流，

对于明渠流，

令式（7）与式（8）相等，可得：

式中：α为表征水流流速作用于泥沙颗粒位置的系数；D为泥沙粒径；下标c表示临界起动状态；ubc为泥沙颗粒处于临界起动状态时的底部作用流速；Uc、U0c分别为冰盖流及明渠流条件下的泥沙颗粒起动流速。

m的取值范围，约为1/5～1/10，通常取1/6［26］。关于m1的取值目前尚缺乏相关研究，应用伯拉修斯公式所得的冰下水流流速分布指数公式中，指数为1/7［22，27］，通过文献［22，28-29］中的59对试验数据应用公式对m1反推，其均值约为1/8，两个m1值均在m的取值范围之内。简化起见，不妨令m1≈m，则：

对于非宽浅的冰盖流，由曼宁公式可得：

式中：n1、n2分别为冰盖及河床的糙率；R1、R2分别为冰盖区、床面区的水力半径。

根据假定，U1=U2=U，令式（11）与式（12）相等，可得：

不妨令非宽浅河道断面形式为矩形，则：

式中B为河道宽度。

联立式（13）-式（16），可得：

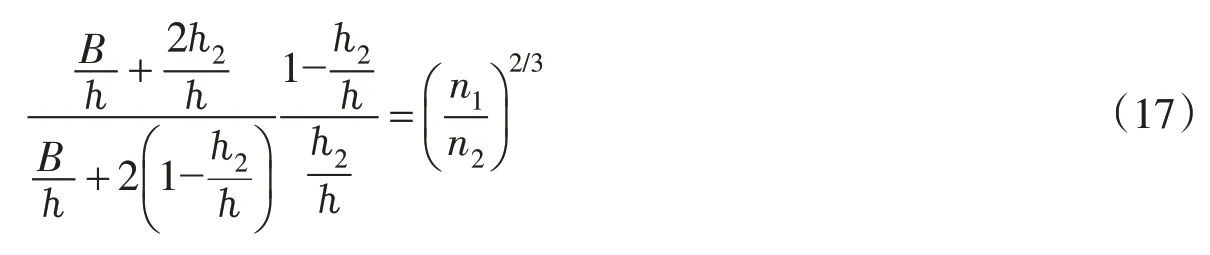
变换后可得：

联立式（10）与式（18），可得：

明渠流中非黏性泥沙颗粒的起动流速采用沙莫夫公式形式：

式中k为起动流速系数。

联立式（19）与式（20），可得：

取m=1/6，k=4.6，则：

该式即为同时适用于非宽浅明渠流及冰盖流的统一泥沙颗粒起动流速公式，当n1=0 时，即为非宽浅河道明渠流的泥沙起动流速公式。这里的泥沙为床面层内可忽略其黏性的散粒体泥沙颗粒，粒径大于0.15～0.20 mm，且不考虑冰期低温对水流黏滞性的影响。

对于宽浅河道，R1≈ ℎ1，R2≈ ℎ2，则可得：

联立式（20）与式（24），可得：

该式即为同时适用于宽浅明渠流及冰盖流的统一泥沙颗粒起动流速公式，当n1=0 时，该式即为宽浅河道明渠流的泥沙起动流速公式。

4 起动流速公式合理性的检验

王军和孙连进在试验水槽中进行了天然无黏性沙的起动试验，光滑冰盖用轻质泡沫模拟，通过在泡沫板中插入竹签的办法来改变其糙率，冰盖糙率有0.0212、0.0322、0.0347三种类型，通过在槽底铺设不同值粒径的天然无黏性沙来实现床面糙率的改变，不同泥沙颗粒的中值粒径分别为0.32、0.85、1.32 mm，对应河床糙率依次为0.0109、0.0128、0.0138［3］。采用所得试验资料，分别对式（22）及式（25）的合理性进行检验。

单个误差率采用如下公式计算：

单个误差率=（计算值—实测值）/实测值×100%

平均绝对误差率采用如下公式计算：

平均绝对误差率=单个误差率绝对值之和/实测数据个数

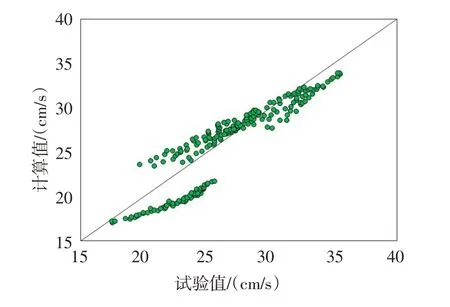
图3 起动流速实测值与式（22）计算值的比较

图4 式（22）起动流速计算值的误差率

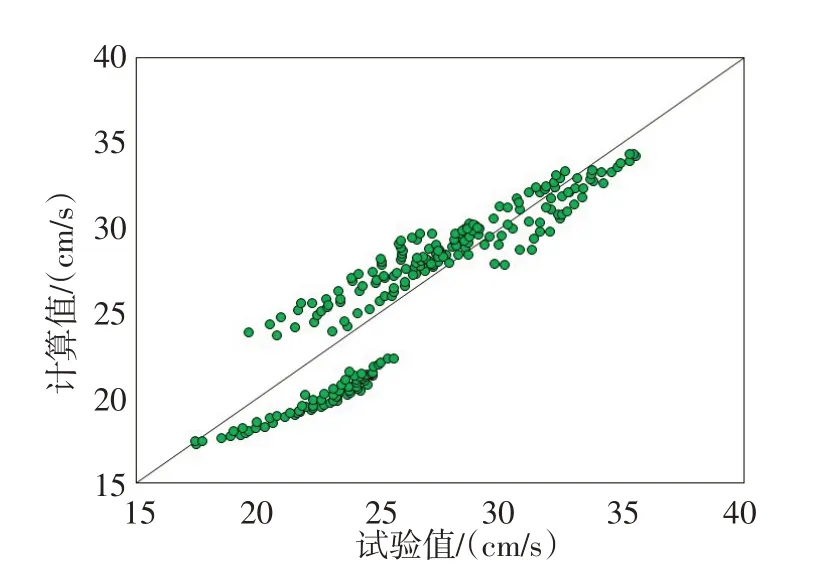
图5 起动流速实测值与式（25）计算值的比较

图6 式（25）起动流速计算值的误差率

图3及图5显示，无论采用采用式（22）还是式（25）来计算冰盖流作用下的非黏性泥沙颗粒起动流速，计算值与实测值整体上符合良好。图4及图6显示，两种计算方法下的误差率均在-16%～21%之间，且大多数在-15%～10%，误差率较小。采用式（22）时平均绝对误差率为7.186%，采用式（25）时平均绝对误差率为7.245%，相差不大，表明边壁效应对冰盖流条件下的泥沙起动流速影响不大。整体上来说，采用式（22）或式（25）来计算冰盖流作用下的非黏性泥沙颗粒起动流速均是合适的。

图4及图6反映出，当床面泥沙粒径为D=0.32 mm时，计算值均比实测值小；当床面泥沙粒径为D=0.85 mm时，计算值均比实测值大；D=1.32 mm时的误差率均分布在0的两侧，误差率比另外两种粒径时低。这说明所得泥沙起动公式对于较粗的泥沙颗粒有更高的精度，更适用于粗颗粒泥沙。另外，王军和孙连进的试验中，冰盖糙率n1均大于河床糙率n2，相当于所得泥沙起动公式仅检验了n1>n2的情形。对于n1≤n2的情形，公式的适用性如何，由于缺乏公开的试验数据，有待进一步检验。

5 明渠流、冰盖流、冰塞条件下的起动流速及可起动最大粒径

当河道沿程同时具有明渠流、冰盖流、冰塞三种条件时，从理论上对三种条件下的起动流速及最大可起动粒径进行分析。

冰塞条件下的泥沙颗粒起动，与冰盖流作用下的泥沙颗粒起动类似，由式（25）可得到类似形式的冰塞条件下的泥沙颗粒起动流速为：

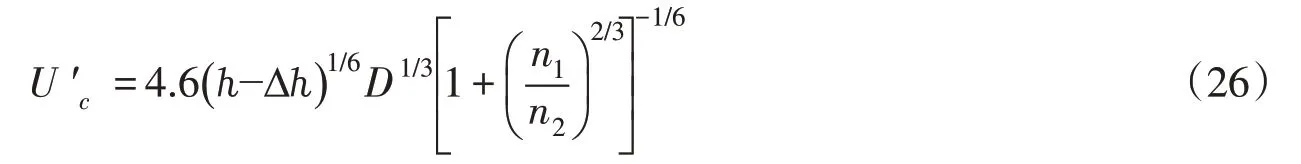
式中：U′c为冰塞条件下的泥沙颗粒起动流速；∆ℎ 为冰塞厚度。

根据式（26），当发生冰塞时，水深ℎ 减小了冰塞厚度∆ℎ，糙率n1增大，这两个因素的改变均会导致起动流速降低，说明发生冰塞条件下床面泥沙颗粒更易起动。由此冰塞时的U′c<冰盖流时的Uc<明渠流时的U0c，即泥沙颗粒在普通冰盖时比明渠流时更易起动，形成冰塞时比普通冰盖流时更易起动。

忽略形成冰盖后的水深变化，那么结冰后在冰盖流条件下垂线平均流速为：

形成冰塞时垂线平均流速U'满足：

联立式（27）、式（28），可得

式中U′为形成冰塞时的垂线平均流速。

根据式（28），形成冰塞后，冰塞部位垂线平均流速大于形成普通冰盖时的垂线平均流速。平均流速增大，而起动流速减小，则显然可以起动的泥沙颗粒粒径将变大。

令明渠流条件下可起动的最大泥沙粒径为Dmax，小于粒径Dmax的沙粒占床面沙粒的ε1，则：

冰盖流条件下，

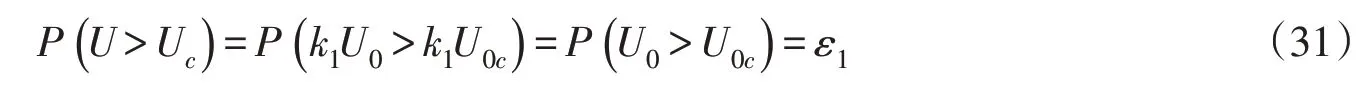
冰塞条件下，

式中：Dmax为明渠流条件下可起动泥沙颗粒的最大粒径；ε1为床面上小于粒径Dmax的沙粒占床面沙粒的比例；P为发生某一事件的概率。

式（30）-式（32）表明，冰盖流与明渠流条件下的可起动最大泥沙粒径相同，但形成冰塞后的可起动最大泥沙粒径将增大，冰塞所在断面将产生冲刷。

6 头道拐河道断面冰期强烈冲淤变化分析

以2014年黄河头道拐断面的冰期实测资料为例，对断面的冲淤机理进行分析。

2014年头道拐断面不同时段冰盖下冰花厚度分布如图7所示。

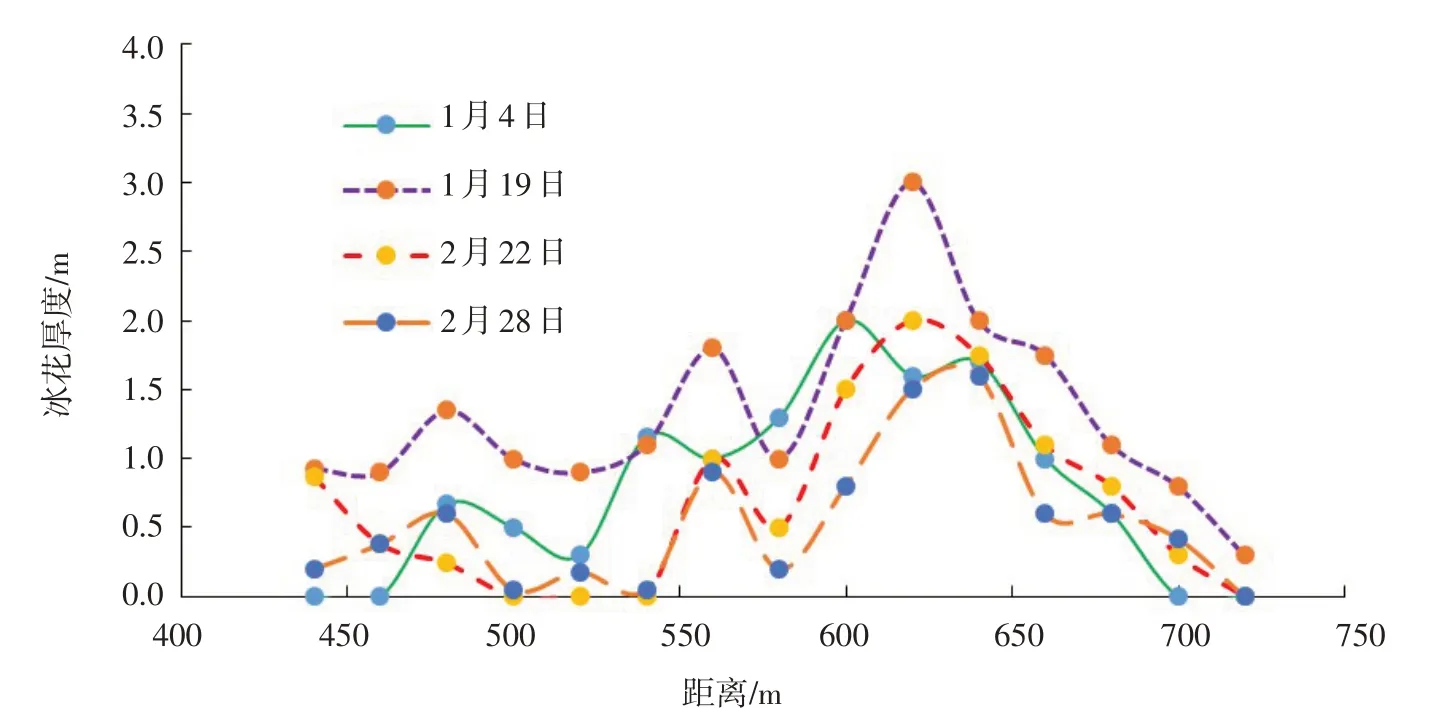
图7 2014年冰期头道拐断面不同时段冰花厚度分布

由图7可知，封河期内右岸附近冰花厚度明显大于左岸，大量冰花集聚在右岸600～700 m范围内，相当于在右岸附近形成了局部冰塞。对比图1和图7可知，由于冰塞的阻水作用，水流被挤压到了左岸附近，左岸附近流速增大导致可起动最大泥沙粒径增大，进而引起左岸附近冲刷。右岸附近冰花厚度在1月19日达到最大约3 m，而后逐渐减小；左岸冲刷深度从1月4日到2月28日均逐渐增大，但2月22日到2月28日间增大速度已趋慢，断面形态已趋于稳定。说明整个时间段内，右岸附近冰花都存在阻水作用，只是随着冰花厚度减小阻水作用减小，左岸冲刷速度变慢了。统计各日期的流量、冰花面积、冰花平均厚度及断面面积等情况，见表1。

表1 2014年冰期头道拐断面不同时刻流量、冰花面积等物理量变化情况

从表1可知，冰期内冰花面积及平均厚度从1月4日到1月19日增大，而后到2月28日减小；断面面积从1月4日到2月22日增大，而后到2月28日减小。二者增减的时间并不完全一致，说明断面面积的增减与冰花面积及厚度的增减并非是同步的，断面面积的增减相对冰花厚度的增减有一个响应和滞后的过程。冰花厚度的增减与冰下断面面积的增减存在正相关关系，冰花厚度的增加引起断面发生冲刷面积增大，冰花厚度的减小引起断面发生淤积面积减小。这与前文的分析，形成冰塞后可起动最大泥沙粒径将增大，冰塞所在断面将产生冲刷是一致的。Zabilansky认为在冰盖作用下水流受到压缩，床面切应力增大从而加剧了床面的冲刷［30］，本质上是相同的。

从表1同时可知，冰期内断面平均流速变化幅度很小，这是由于流量及净过水面积几乎也在同步增减。从1月4日到2月28日，断面面积及净过水面积均逐渐增大，冰花面积从1月4日到1月19日逐渐增大而后逐渐减小（见图8）。1月4日到1月19日，净过水面积增加了46.9 m2，冰花面积增加了149.7 m2。冰花面积的增加会使净过水面积减小，但实际上净过水面积却增加了，净过水断面面积的变化是由冰花面积及河床冲淤面积的变化共同引起的，则河床应冲刷了196.6 m2，河床冲刷对净过水面积的增加为正贡献，冰花面积增加为负贡献。1月19日到2月28日冰花面积减小了226.7 m2，净过水面积则增加了344.5 m2，净过水断面的增加面积大于冰花的减小面积，差值117.8 m2应由河床冲刷所贡献，冰花面积的减小对净过水断面的增加的贡献率约为2/3，河床冲刷对净过水断面的增加的贡献率约为1/3。总体来说，流量及净过水面积几乎同步增减导致断面平均流速变化不大，冰花面积先增后减，净过水面积不断增加，使河道断面整体上始终处于冲刷状态。

图8 2014年冰期头道拐断面不同时段断面面积、净过水面积、冰花面积变化

冰塞在右岸附近形成，冲刷在左岸附近形成，二者形成的位置在断面上的分布刚好是相反的。由于是天然河道断面，流速及冰花厚度在横向上分布不均，导致可起动最大泥沙粒径在横向上分布不均，从而断面各处的冲淤变形有很大差异。形成冰塞后冰下断面整体上以冲刷为主，可能发生局部小范围淤积。

7 结论

探讨了冰盖流条件下床面上非黏性泥沙颗粒起动的力学机制，冰盖的存在并不改变泥沙颗粒起动所需的底部流速的大小，只是改变了床面附近以及整个垂线上的流速分布。基于Einstein假定，推导得到了同时适用于明渠流及冰盖流的统一的非黏性泥沙颗粒起动流速公式，所得公式与已有试验数据符合良好。当冰盖糙率为0时，冰盖流泥沙颗粒起动流速公式即退化为明渠流泥沙颗粒起动流速公式。边壁对公式计算值有一定影响，但对平均误差率影响不大。对于起动流速的大小，明渠流>冰盖流>冰塞，对于可起动最大泥沙粒径，明渠流=冰盖流<冰塞。冰期河道断面同样可能存在强烈的冲淤变化，这是冰花集聚形成冰塞引起可起动最大泥沙粒径增大所致。