动态循环荷载下大坝混凝土拉压转换损伤本构模型构建及影响研究

涂 劲，李德玉，郭胜山，李春雷，王海波

（中国水利水电科学研究院工程抗震研究中心，北京 100048）

1 研究背景

高混凝土坝强震响应分析属于多介质耦合的强非线性动力问题，其中大坝混凝土损伤开裂发生发展的演化过程是研究重点之一［1-2］。构建大坝混凝土动态损伤演化数值模型是以计算分析手段研究地震作用下混凝土坝地震损伤演化、评价大坝抗震安全的基本前提。在一些混凝土结构的动态损伤分析中，常使用弹性损伤本构模型［3-5］和弹塑性损伤本构模型［6-7］，国内学者也将其用于大岗山拱坝等实际大坝工程的非线性动力分析中［8-10］。但是弹性损伤本构模型不能考虑材料损伤后发生的残余变形，而弹塑性损伤模型虽考虑了残余变形，但其基于塑形理论的残余变形计算较适用于描述由晶体滑移错位形成塑性流动的金属材料，而不适于由微裂缝拓展导致损伤的混凝土材料，因此一些学者从试验入手，探究新的方法。文献［11-12］提出了基于材料试验成果建立、计入残余变形影响的大坝混凝土动态损伤演化模型，考虑混凝土动态受拉损伤，可根据在单轴受拉循环荷载作用下的试验资料，直接求得损伤过程中残余变形的增长以及卸载与再加载过程中考虑残余应变影响的非线性损伤弹性模量，从而避免套用并不适用于混凝土的塑性理论，并使损伤演化规律更符合试验结果，计算也大为简化。但是在受拉损伤后，从受拉状态转为受压状态时，该模型参考ABAQUS程序考虑“单边效应”，认为受压时弹性模量会立即恢复至初始值，在受压状态中始终保持受拉残余变形。

混凝土受拉损伤后进入受压状态时弹性模量立即恢复的数值模型与实际情况不符，实际材料试验的拉压转换应力-应变曲线显示混凝土进入受压状态后受压模量并非立即恢复为初始弹性模量，而是由损伤后弹性模量连续渐进恢复至初始弹性模量，其间原有的受拉残余应变在压应力作用下迅速减小到较小数值，而这一过程将对大坝在地震往复荷载作用下的力学性能有重要影响。本文提出受拉损伤后拉压转换时受压应力应变关系采用双折线模型，给出拉压转换时应力-应变关系表达式，构建更接近混凝土拉压转换时真实状况的数值模型，并通过实际工程的计算分析，认为原有的受压弹性模量直接恢复的数值模型过高估计了坝体刚度，可能带来偏于不安全的动力分析结果。

2 基于材料试验构建大坝混凝土损伤演化模型

混凝土的单轴拉、压试验数据表明，其损伤后卸载和再加载的过程中，不可恢复的残余变形随损伤程度而增长，其影响不容忽视。混凝土作为非均质准脆性材料的损伤，是由于其中的微裂缝在荷载作用下继续萌生和拓展，形成宏观裂缝并不断发展最终导致结构失效破坏。混凝土中的微裂缝是随机分布的，且裂缝尖端并不存在均匀的应力场，难以采用断裂力学的方法解决，其损伤过程也不同于金属材料基于晶体滑移或错位的塑性微观现象，因而把混凝土损伤变形中的残余应变部分作为符合塑性理论的塑性变形缺乏依据和试验验证。文献［3］提出，可根据在单轴拉、压循环荷载作用下的试验资料，直接求得损伤过程中残余变形的增长，以及卸载与再加载过程中考虑残余应变影响的非线性损伤弹性模量，从而避免套用并不适用于混凝土的塑性理论，不仅计算过程得以简化，而且使损伤演化规律更符合试验结果。

图1为基于混凝土单轴拉伸试验的σ-ε曲线建立的动态受拉损伤本构数值模型。残余应变εp为：

图1 大坝混凝土动态受拉损伤本构数值模型

式中：E0为初始弹性模量；ε为发生损伤后的总应变；εe为对应初始弹性模量的弹性应变；dt为损伤因子。

产生受拉损伤后，当卸载和再加载的应力未超过初始卸载应力时，其应力σ为：

由此得实际的视弹性模量：

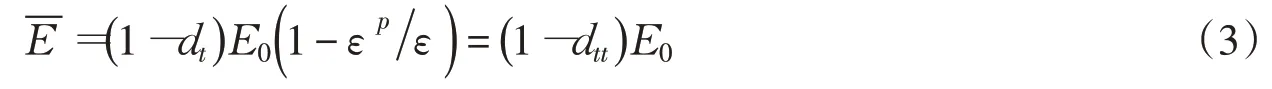
视损伤因子dtt则为：

式中dc、dt分别为受压损伤因子和受拉损伤因子。

相应的等效损伤弹性模量为：

混凝土坝在其抗震设计中是作为二维或三维体系考虑的，故以有效应力表征的多维体系复杂应力状态下的三维空间屈服面可作为判断其损伤的损伤面，通常采用Lubliner等［13］和Lee等［6］所建议的函数：

式中：I1为第一应力张量不变量；J2为第二应力偏量不变量；α=（fbo-fco）/（2fbo-fco），fbo为双轴抗压强度，fco为单轴抗压强度，一般取fbo/fco=1.16，故α=0.12；，Cc、Ct分别为有效抗压强度和有效抗拉强度。

为把单轴试验的损伤演化规律应用于多维体系的应力状态中，目前大多采取以多维体系中的最大和最小主应变εmax和εmin替代单轴受拉和受压试验中的εt和εc，但由于混凝土的拉压损伤演化规律的差异，引入了一个考虑复杂应力状态时的拉、压应力间相互影响的加权因子：

由于混凝土抗压强度远高于抗拉强度，在暂不考虑受压损伤时，最终在多维体系中采用的等效弹性模量为：

当卸载至拉应力趋于零时，εmax接近εp，在多维体系中用等效弹性模量求得的应变张量εij即为初始卸载应力相应的残余应变张量，其相应的变形张量为。εmax小于εp时，多维体系转向受压为主的情况，按等效初始弹性模量对自变量u-up求解。考虑残余应变的混凝土损伤模型完全不涉及塑性理论，概念清晰合理，计算也更为简便。

本文在1500吨MTS大型材料动态性能试验机上进行某大坝全级配混凝土轴拉全过程试验，试验采用“加卸载非等速率”的控制方式［14］获得动态的轴拉加卸载循环应力应变全过程曲线如图2，其中引伸计数据给出的位移-荷载曲线图形更为稳定完整，故采用引伸计数据转换作为测定的应力应变全过程曲线试验数据，经统计回归整理得到典型应力－应变全过程曲线，包括应力-应变关系包络线和卸载、再加载的往复循环曲线的数学表达式。

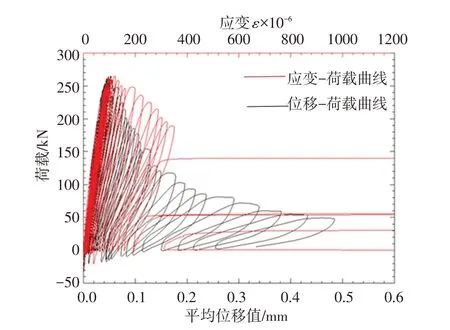
图2 全级配混凝土试件轴拉加卸载循环应力应变全过程曲线

超过峰值应力之后，应力-应变关系包络线采用下式表达：

式中：σp为峰值应力；k、λ为系数，可根据试验得到的试件到达峰值强度后的断裂能确定，数值越大下降段断裂能越小，对多个试件给出的全过程曲线拟合应力应变包络线的各项参数，最终确定的整组试件应力应变全过程包络线的k值为1.78，λ取1.22。

设卸载点为（σun，εun），卸载到零应力点的残余应变为εp，通过同组多个试件的残余应变与卸载应变的试验数据统计回归，可得到残余应变εp与卸载应变εun关系如下式：

根据轴拉试验资料给出的到达峰值应力后的应力应变包络曲线（式（10））和该曲线上某点开始卸载时卸载应变与卸载至零应力的残余应变的关系曲线（式（11）），结合混凝土的动态抗拉强度及动态弹性模量，得到以卸载应力-开裂（损伤）位移关系（σ-wcr）和损伤因子-开裂（损伤）位移关系（d-wcr）来表征的动态损伤演化规律曲线（如图3）。

图3 大坝混凝土动态损伤演化规律曲线

3 大坝混凝土受拉损伤后拉压转换本构数值模型

3.1 拉压转换处理 在单轴循环加载条件下，刚度退化机制比较复杂，它涉及到预先存在裂纹的开闭问题和裂纹间的相互作用问题。试验观察发现，当循环加载的应力符号变号，即反向加载的刚度有所恢复，这种刚度恢复也称之为“单边效应”，它是混凝土循环加载的一个显著特点。特别是当应力由拉变为压时，效应较明显，这时压应力使得受拉形成的裂纹闭合从而使受压刚度得到恢复。目前的数值模型（包括ABAQUS程序中弹塑性损伤模型）均采用引入权系数wc控制应力反向即由拉转压时的刚度恢复能力［15-18］，以单轴状态为例，拉压转换时的损伤因子为：

wc=1，那么d=0，材料恢复到受压无损状态E=E0；若wc=0时，d=dt，材料没有刚度恢复；当wc在0～1之间取值时，表示刚度部分恢复。对于受拉损伤后进入受压状态，目前常用的取值为wc=1，即一旦进入压应力区则受压刚度完全恢复。无论何种取值，在受压加载阶段的刚度均保持不变。

既然混凝土受压刚度恢复的所谓“单边效应”是由于受拉形成的裂纹闭合产生，裂纹的闭合是个渐进的过程，而进入压应力状态刚度立即恢复的模型显然无法反映这一过程，而wc在0～1之间取值时又无法反映在进入稳定受压阶段后混凝土弹性模量基本完全恢复这一现象，故需研究提出反映大坝混凝土受拉损伤后受压刚度恢复过程的本构数值模型。

3.2 拉压转换本构模型 图4 为全级配混凝土试件轴向拉压循环试验获得的的应力-应变全过程曲线。由图4可见，在发生受拉损伤后，即拉应力峰值过后进行卸载并到达压应力区时，受压弹性模量并非立即恢复，也不是保持某一数值不变，而是以渐进的形式，随着压应力的增加，逐渐由受拉损伤后的弹性模量恢复至初始弹性模量。显然，受压弹性模量固定不变的假定与试验给出的实际情况不符，尤其是认为受压弹性模量立即完全恢复的简化方式，有可能过高估计混凝土材料进入受压区后的刚度，而偏于不安全。

图4 全级配混凝土试件轴向拉压循环的应力-应变全过程曲线

为建立拉压转换本构关系的数值模型，既需考虑混凝土材料受拉损伤后进入受压状态时弹性模量逐渐恢复的过程，又需考虑计算分析中数值模型的简易可行，因为考虑材料动态损伤后的本构关系数值模拟已相当复杂，再采用过于繁琐的拉压转换模拟会给计算分析带来较大困难及计算耗时的过度增加。因此，如图5所示，本文对试验给出的全级配混凝土试件轴向拉压循环的应力-应变全过程曲线在受压阶段的应力-应变关系采用折线形式进行简化，即在初始进入受压状态时受压弹性模量为损伤弹性模量，应力应变为线性关系，在压应力增加受压弹性模量恢复至初始弹性模量后，做斜率为初始弹性模量数值的直线与零应力点引出的损伤弹性模量直线相交点为应力应变关系转折点，从而得到双折线形式的拉压转换应力应变本构模型，该转折点对应的拉应变数值εq即为受压刚度恢复应变。

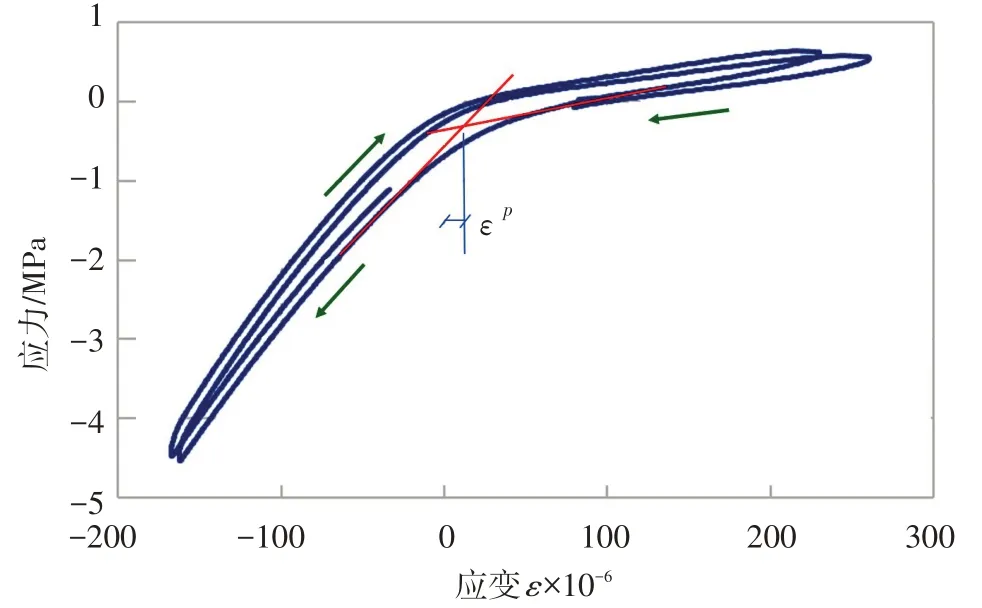
图5 拉压转换应力-应变关系的简化

受拉损伤后，当卸载至拉应力趋于零值时，εt接近εp（对应多维体系时，εmaxt接近εp，此时多维体系中的应变矢量ε即为该初始卸载时对应的残余应变矢量εp）。当εt小于εp时，从受拉转向受压，依据试验结果，刚度未立即恢复，基本保持受拉损伤后的刚度，直至εt达到较小值其刚度才逐渐恢复，随着压应力的逐渐加大，受压刚度渐渐恢复到初始刚度。

为考虑受压刚度逐渐恢复的过程，同时尽可能便于计算分析，在压应力区以图6 折线形式的应力-应变关系近似反映受拉损伤后拉压转换时的本构模型。由试验数据直接给出不同残余应变时相应的双折线拐点对应的拉应变数值εq（受压刚度恢复应变），则单轴条件下，进入压应力区后的应力-应变关系可描述为：

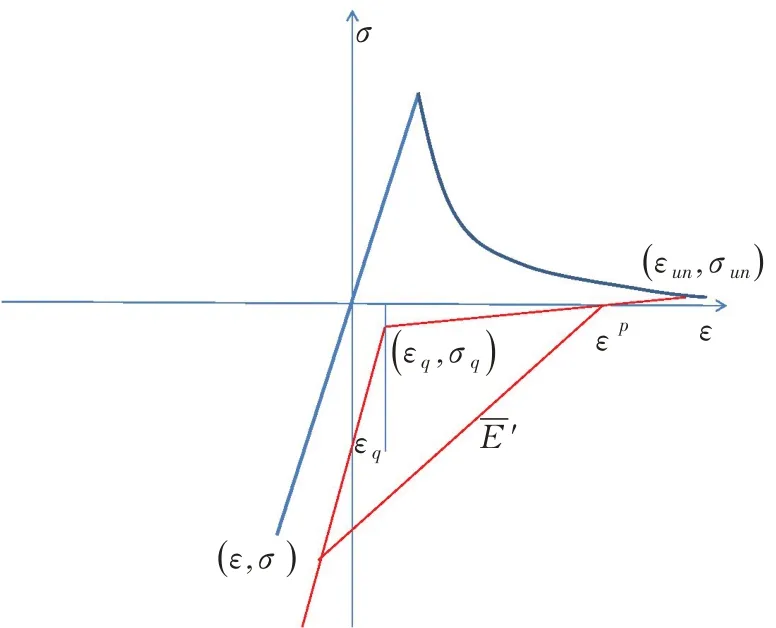
图6 拉压转换中的应力-应变关系

当ε >εq时，

当ε≤εq时，

由此计算从（εp，0）点起始的视弹性模量为：

当ε >εq时，

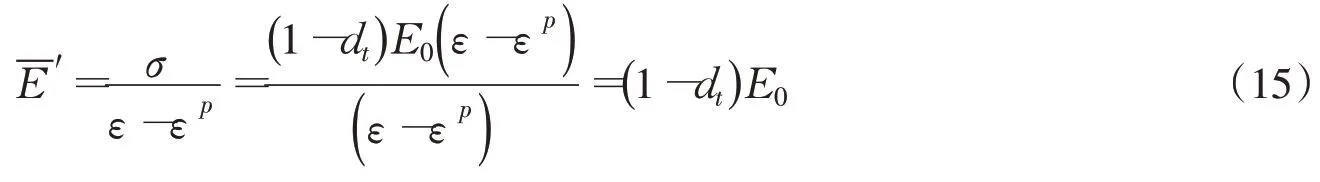
当ε≤εq时，

设此时相应的视损伤因子为dtc，则有：

即拉压转换时的视损伤因子dtc为：

在ε >εq时，

在ε≤εq时，

本构方程为：

对应多维体系，当εmaxt小于εp时，材料进入受压状态，设等效损伤因子为d，本构方程为：

式中：1-d=（1-r）（1-dtc），r为多轴到单轴转换的受拉权重因子，此时r=0；D为对应多维体系的弹性矩阵。

由以上推导可见，对不同的卸载拉应力，仅需确定其相应的受压刚度恢复应变εq，配合受拉损伤本构关系中给出的残余应变εp，则可建立受拉损伤后进入受压状态时的本构关系数值模型。

本文对于图4给出的拉压全过程曲线进行拟合分析，建立以如图3应力-开裂（损伤）位移变化关系（σ～wcr）和损伤因子-开裂（损伤）位移变化关系（d～wcr）来表征的混凝土的动态受拉损伤演化规律曲线及如图7的受压刚度恢复应变-残余应变关系（εq～εp）表征的受压刚度恢复特性曲线。计算中根据不同的卸载应力、应变数值，插值得出其相应的残余应变εp及受压刚度恢复应变εq，代入式（15）—（17），即可求得相应的视弹性模量和视损伤因子，进而完成位移、应力等的求解。

4 实际工程应用及比较

为检验由本研究建立的拉压转换本构模型对实际大坝强震中损伤发展状况数值模拟结果的影响，进行了某重力坝在设计地震作用下的损伤分析。坝体混凝土材料采用上文所列由试验获取的本构参数，分别采用上节建立的双折线形拉压转换本构模型及原来的受压刚度完全恢复的本构关系数值模型，并将二者结果进行比较。

某混凝土重力坝挡水坝段坝高185.0 m，坝顶宽度为16.0 m，坝底宽度为165.5 m。地基模拟范围沿深度方向和上下游方向均取2 倍坝高。坝体单元尺寸在2 m左右。计算模型以黏弹性人工边界模拟无限地基辐射阻尼作用。

建基面高程为1970 m，坝顶高程为2155 m，上游正常蓄水位2150.0 m，下游水位2019.25 m，淤沙高程为2023.7 m，淤沙浮容重为8 kN/m3，淤砂内摩擦角12°，混凝土容重取24 kN/m3，水的容重取9.8 kN/m3，岩石的密度为2777 kg/m3。图8为该重力坝挡水坝段剖面图。计算中受拉损伤本构均采用试验给出的数值关系，在拉压转换的模拟中方案1为受压后弹性模量立即恢复为初始弹性模量，方案2为按照图7给出的受压刚度恢复应变εq作为刚度恢复的拐点，求取受压阶段的视损伤因子和视弹性模量，分别进行分析。计算采用的地震动输入为由场地相关设定地震反应谱拟合生成的人工地震波，并在工程相应设计地震峰值加速度水平的基础上，放大不同的超载倍数至大坝坝体损伤出现上下游贯通。

图8 某重力坝挡水坝段（单位：m）

计算中方案1在设计地震1.3倍超载工况时发生头部损伤上下游贯通如图9，而在与此相同地震荷载作用下，方案2的坝体损伤分布则如图10所示。由图中可见，采用本文建立的拉压转换本构模型较通常采用的受压刚度完全恢复的模型计算所得坝头折坡部位损伤区有明显扩大，其原因应为受拉损伤的区域进入受压状态时刚度的降低将使受拉侧的混凝土受力增加，损伤范围可能加大，而同时由于地震的往复作用，最终坝头折坡处的混凝土损伤区域明显增大。由此表明：（1）受压刚度立即完全恢复的本构模型过高估计了坝体刚度，不符合坝体混凝土受拉损伤后的实际情况；（2）在地震往复荷载作用下，结合试验结果建立的受压刚度恢复模型计算结果表明，大坝损伤区更为集中，容易形成坝体上下游贯通的大范围损伤；（3）大坝抗震安全分析中建议考虑这一因素，否则计算结果可能偏于不安全。

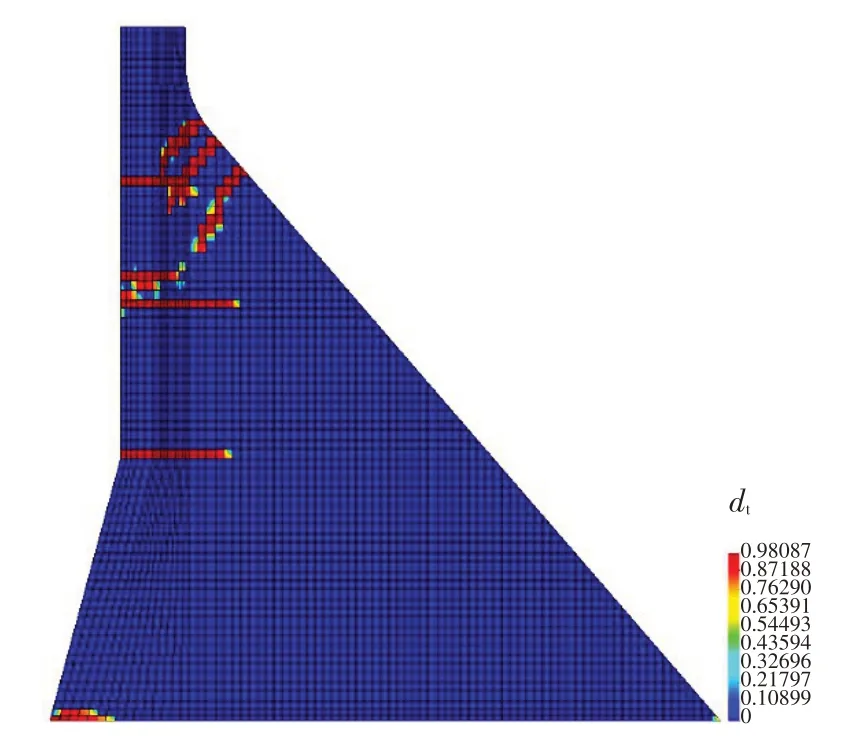
图9 坝体震后损伤分布（方案1）

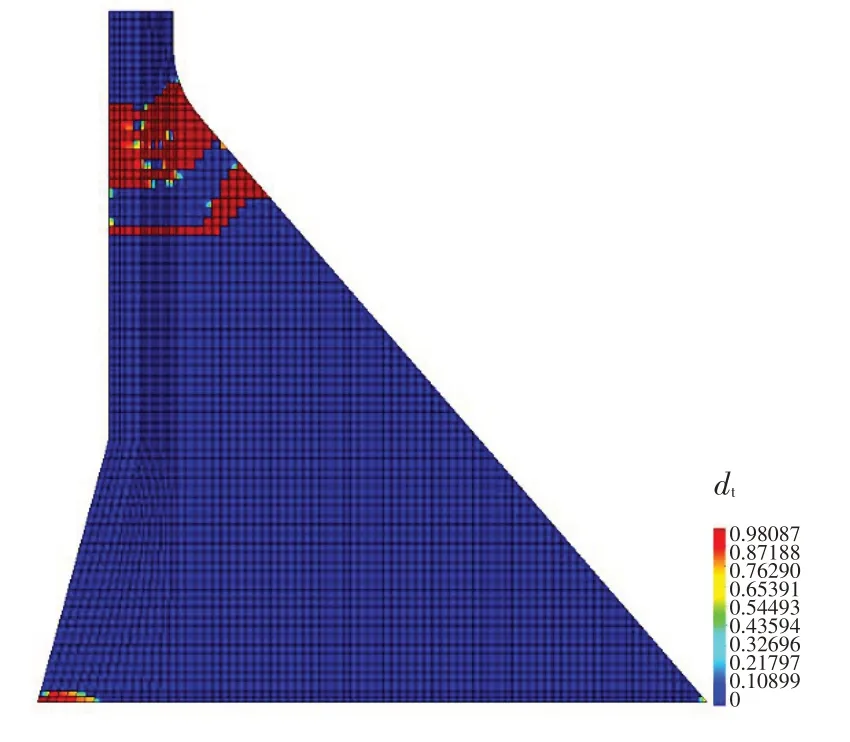
图10 坝体震后损伤分布（方案2）

4 结论

材料拉压转换全过程试验结果的分析表明，混凝土受拉损伤后进入受压状态时弹性模量立即恢复的数值模型与实际情况不符，实际材料试验的拉压转换应力-应变曲线显示混凝土进入受压状态后受压模量并非立即恢复为初始弹性模量，而是由损伤后弹性模量连续渐进恢复至初始弹性模量，期间原有的受拉残余应变在压应力作用下迅速减小到较小数值，而这一过程将对大坝在地震往复荷载作用下的力学性能产生重要影响。故本研究根据试验曲线提出了受拉损伤后拉压转换时受压弹性模量采用双折线模型的思路，给出拉压转换时应力-应变关系，构建了更接近混凝土拉压转换时真实状况的应力-应变关系数值模型，并通过实际工程的计算分析，指出原有的受压弹性模量直接恢复的数值模型过高估计了坝体刚度，可能带来偏于不安全的动力分析结果，故建议应改进混凝土大坝-地基系统中混凝土动态损伤模拟中拉压转换本构关系数值模型，以更真实地反映受拉损伤后的大坝地震响应工作性态。