矿用不确定性电液系统的预测控制

张志忠

（大运华盛老窑沟煤业有限公司，山西 宁武 036700）

引言

电液系统以其响应速度快、功率重量比大以及能够提供大的源动力[1-2]等优点被广泛应用于工业生产和工业制造，包括重型机械和航空航天飞行控制执行器。然而，电液系统中各性能参数存在许多非线性问题，如伺服阀流量与压力之间的非线性关系、负载与导轨之间的非线性摩擦等。这些非线性问题给高性能控制器的设计带来了较大困难。电液系统还具有参数不确定性，例如液压油的有效体积模量会因油温和夹带空气的波动而变化，而参数的变化会对跟踪精度产生很大的扰动[3]。就电液系统的这种不确定性，已有很多研究，例如：采用反步自适应模糊滑模控制器来消除电液系统中的抖振和减小参数不确定性[4]；将摩擦和负载视为电液系统中的外部干扰，提出了一种滑模变结构控制方法，使采矿机械臂精确跟踪所需位置；自适应积分控制器的提出将未建模非线性摩擦和负载变化等外部干扰作为建模参数，以便惯性负载由一套液压旋转执行机构可以跟踪运动轨迹[5]；利用Nussbaum 函数计算伺服阀的控制电压，为具有参数不确定性和负载扰动的电液执行器设计饱和自适应控制器跟踪位置[6]。本文的目标是设计一种低成本、尽可能接近目标轨迹的电液控制系统。

1 PDV 调节电液系统模型

单杆电液系统原理图如图1 所示。由电动机驱动泵将油从油箱中抽出之后，油通过止回阀流入PDV。通过调节施加在PDV 电磁阀上的控制电压，可以改变油的流量和方向。油流过PDV 进入气缸，活塞就可以驱动负载移动。

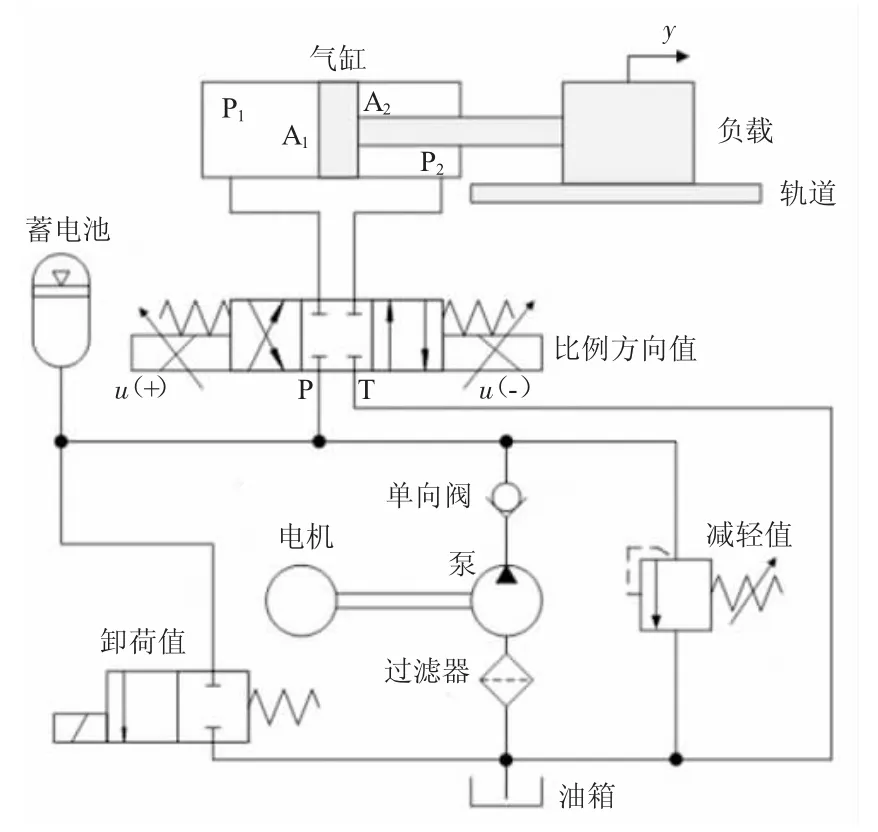
图1 电液系统原理图

根据牛顿第二定律，负载的动力学可以表示为：

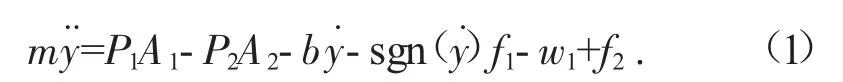
式中：m 为荷载质量；y 为荷载位移；P1为帽侧腔内压力；P2为杆侧腔内压力；A1为帽侧冲压面积；A2为杆侧冲压面积；b 为活塞与气缸之间的模型阻尼系数；sgn 是符号函数；f1为载荷和轨道之间的滑动摩擦力，f1=μmg，μ 为滑动摩擦系数，g 为重力加速度；w1是电液系统整体受到的外部空间干扰因素，此处为大气压力；f2是负载于轨道之间的非线性摩擦力。

2 控制器的设计

2.1 特征模型

从电液系统的数学模型可以看出，由于比例换向阀存在较大的死区，使得对负载跟踪所需轨迹的控制设计比较困难。此外，电液系统在工作过程中，许多参数也会发生变化，例如，液压油的有效体积模量会因温度变化和夹带空气而发生变化。特征模型是描述参数随时间变化的非线性系统的慢时变差分方程，因此通过自适应调节参数来逼近原电液系统。

本文采用二阶差分方程作为特征模型来描述电液系统的输入与输出关系，其特征模型如下：

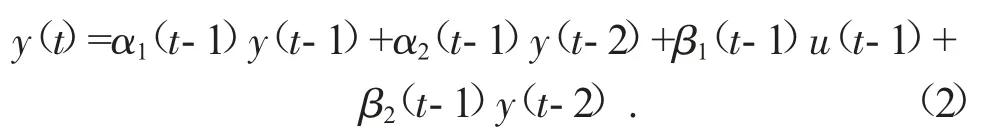
式中：y 为荷载位置；u 为施加在比例换向阀上的控制电压；α1、α2、β1、β2均为时变系数。

2.2 系数识别

根据电液系统的输入和输出能够确定CM模型的参数，同时也可以根据CM特征模型的参数来推测电液真实系统的输入值和输出值。

广义预测控制（GPC）方法是由Clarke 等人提出的。该方法已被广泛应用于工业和学术界。在广义预测算法中，自回归积分移动平均（CARIMA）模型被应用于许多不稳定扰动的工业应用中。由于我们已经得到了电液系统的特征模型，因此可以将特征模型转化为CARIMA 模型，从而使用GPC 方法计算控制电压u（t）。图2 给出了基于特征模型的广义预测控制电液位置控制系统。

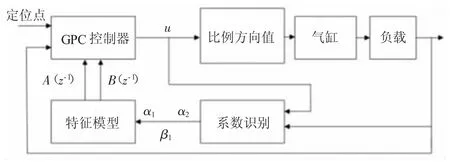
图2 基于特征模型的广义预测控制电液位置控制系统框图

3 实验部分

3.1 死区补偿

比例换向阀存在死区。为了比较死区补偿的能力，采用了比例积分导数（PID）控制器和基于特征模型的GPC（CM-GPC）控制器来计算PDV 电磁阀的控制电压。PID 控制器参数为kp=150、ki=90、kd=2。CM-GPC 控制器参数为α=10-4。图3 描述了使用PID 控制器和CM-GPC 控制器时负载的位置。PID控制器和CM-GPC 控制器的跟踪误差如图4 所示。

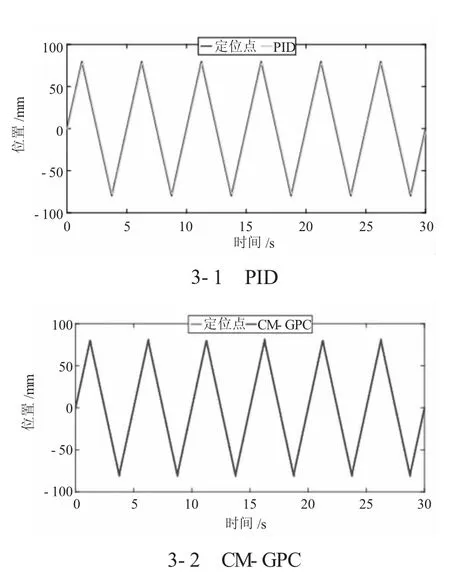
图3 使用PID 和CM-GPC 控制器时负载的位置

从图4 可以看出，CM-GPC 控制器的跟踪误差小于PID 控制器的跟踪误差。

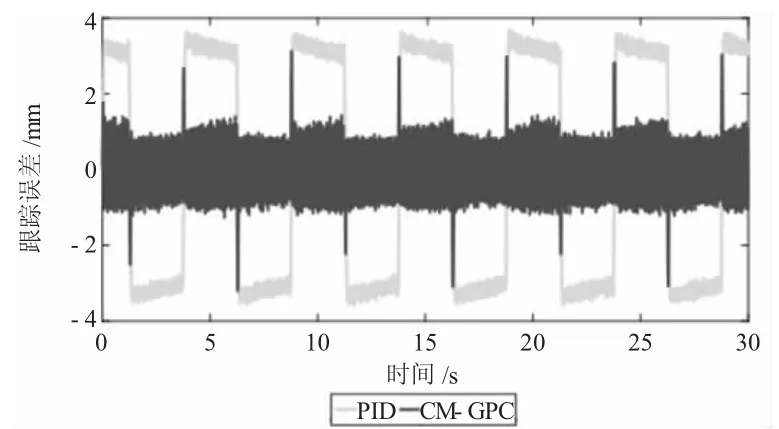
图4 PID 控制器和CM-GPC 控制器的跟踪误差

3.2 有效体积模量波动的抗扰性

液压油的有效体积模量随油温和夹带空气的变化而变化，可以将有效体积模量的波动看作扰动。通过仿真比较了PID 控制器和CM-GPC 控制器的抗干扰性能。在仿真中，期望轨迹为80sin（5πt）描述的正弦曲线，PID 控制器参数为kp=160、ki=50、kd=1.8，CM-GPC 控制器的参数为α=10-6、λ=10-15、λ1=0.01。

图5 为分别使用PID 控制器和CM-GPC 控制器时油液体积模量波动的负载位置，说明了有效体积模量变化时PID 控制器和CM-GPC 控制器的跟踪误差及性能。

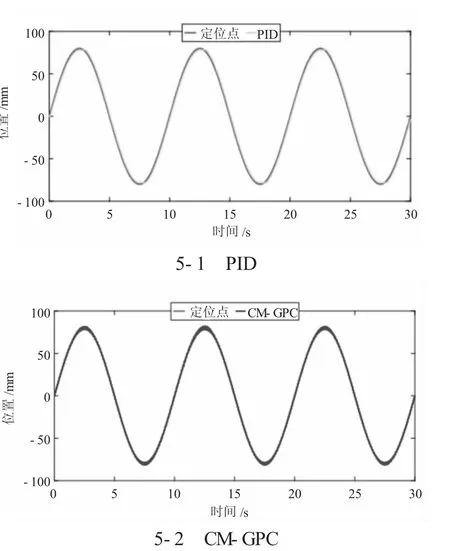
图5 使用PID 控制器和CM-GPC 控制器时负载的位置

当期望轨迹为正弦波且有效体积模量变化时，采用CM-GPC 控制器的电液系统能够比基于PID的电液系统更准确地跟踪期望轨迹。

如下页图6 所示为当期望轨迹为方波、有效体积模量随时间变化时，PID 控制器和CM-GPC 控制器分别控制电液系统的加载位置。可以看出，CM-GPC 控制器控制的电液系统比PID 控制器控制的电液系统更快、更准确地跟踪方波。

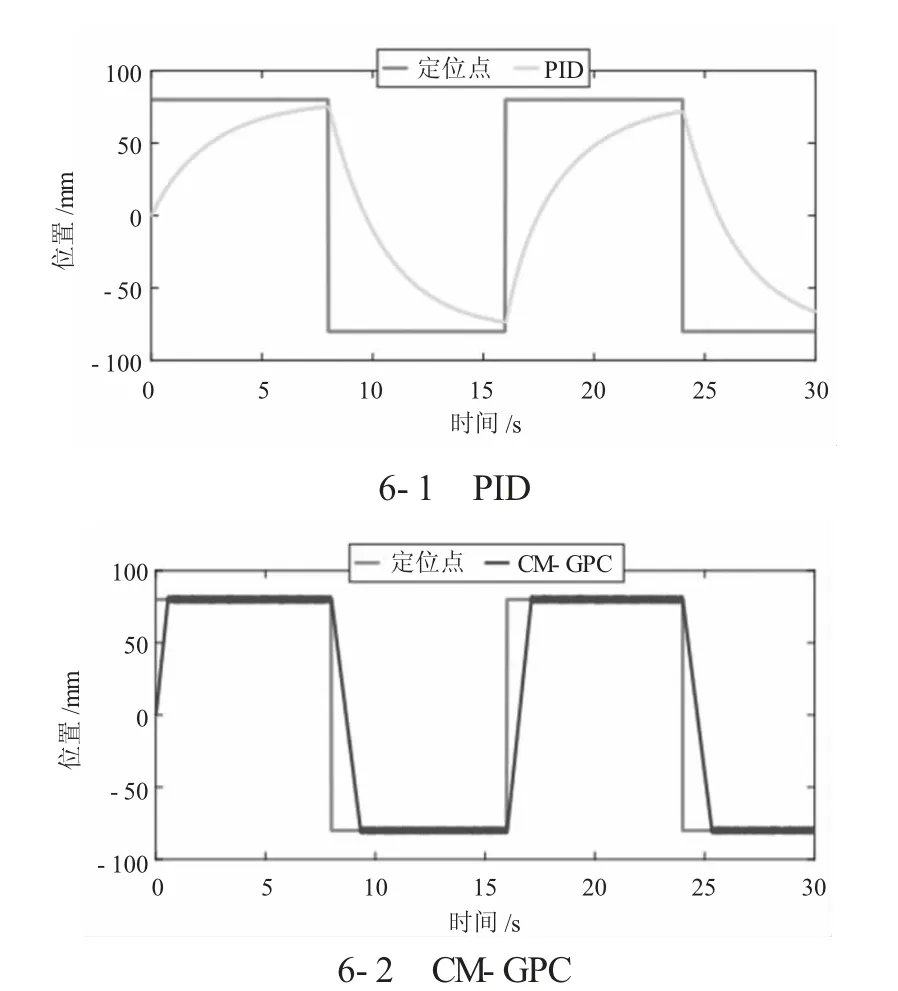
图6 当期望轨迹为方波时由PID 控制器和CM-GPC 控制器控制EHS的负载位置

4 结论

为了补偿电动汽车调节电液系统过程中的死区和参数不确定性，采用基于特征模型的GPC 控制器计算电动汽车电磁阀的控制电压。仿真结果表明：

1）基于特征模型的GPC 控制器具有较强的死区补偿能力；

2）当系统参数发生变化时，与PID 控制器相比，基于特征模型的GPC 控制器能够更精确地跟踪目标轨迹。