外贴CFRP加固RC连续梁的抗弯性能及弯矩重分布分析
张智梅 程 雯
(上海大学土木工程系,上海200444)
0 引 言
碳纤维(CFRP)具有高强、耐腐蚀、轻质等突出优点,被广泛运用于各类钢筋混凝土受弯构件的加固中[1-5]。对外贴CFRP加固RC梁的探讨主要在简支梁方面[6-7],然而,在实际工程中需要加固的受弯构件大多为RC连续梁。在结构工程中,RC连续梁的受损破坏在一定程度上会引起整个结构的倾覆。因此近年来国内外学者开始重视对外贴CFRP加固连续梁的研究[8-12]。
分析现有的研究成果可以发现,首先,对外贴CFRP加固连续梁的研究集中在试验上[10-12],而关于有限元模拟及理论分析的研究较少;其次,外贴CFRP加固RC连续梁呈现显著的弯矩重分布,但仅有少量学者讨论连续梁的内力重分布[13];最后,《混凝土结构加固设计规范》(GB 50367—2013)[14]并没有对外贴CFRP加固RC连续梁的弯矩调幅系数给出明确的数值。若明确外贴CFRP加固RC连续梁的弯矩重分布,便可将按弹性方法计算的弯矩通过弯矩调幅系数进行调整,从而合理地评估结构的承载力,实现设计的优化。
为此,本文首先利用ABAQUS模拟CFRP加固RC连续梁;其次在分析模型上进行影响参数分析,研究各参数对CFRP加固RC连续梁抗弯性能的影响;最后提出连续梁极限破坏时跨中弯矩调幅系数及中支座弯矩调幅系数随CFRP粘贴长度变化的公式,并利用已有的试验数据进行验证,为实际工程设计提供理论依据。
1 非线性有限元数值模拟
1.1 试验概况
本文选用文献[15]中的4根连续梁E1至E4建立有限元模型,试验中E1为未加固梁,E2为负弯矩区加固梁,E3为正弯矩区加固梁,E4为正、负弯矩区同时加固梁。梁的尺寸、加固位置、截面配筋如图1所示,图中P代表竖向外加荷载,L1和L2分别表示负、正弯矩区CFRP黏结长度,其中L1和L2长度分别为2 500 mm及3 500 mm,CFRP板厚度为1.2 mm。材料的具体数据如表1所示。
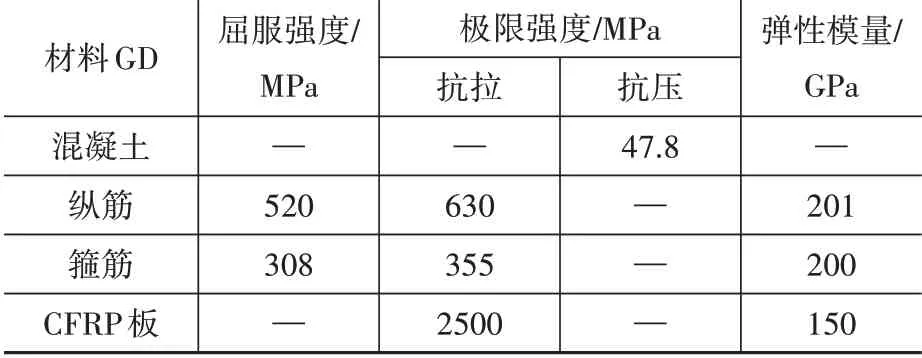
表1 材料的力学性能Table 1 Mechanical properties of materials
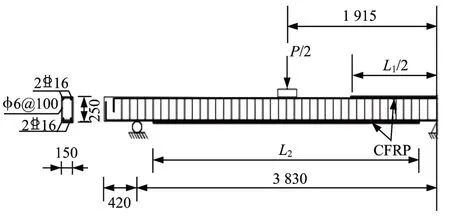
图1 加固梁简图Fig.1 Test piece and reinforcement diagram
1.2 有限元模型的建立
本文应用ABAQUS软件模拟了连续梁E1至E4。建模时,混凝土的本构用ABAQUS中的塑性损伤模型,其受拉和受压应力-应变本构分别选取混凝土结构设计规范[16](以下简称规范)中相应的混凝土单轴受拉和受压本构,并用C3D8R三维实体单元来模拟;钢筋的本构用规范中有加强段的双线性弹塑性模型,用T3D2桁架单元来模拟;CFRP板按线弹性材料设置本构,并用C3D8R单元模拟;为了避免产生应力集中现象,在支座处和跨中加载点处分别设置线弹性刚垫块,其单元类型为C3D8R。
本模型假设钢筋-混凝土界面和CFRP-混凝土界面之间均不发生黏结滑移,故建模时钢筋与混凝土采用内置(Embedded)约束;CFRP与混凝土采用绑定(Tie)约束;垫块与梁的接触采用绑定(Tie)约束;垫块与加载点采用耦合(Coupling)约束。根据连续梁实际约束情况,将中支座设置为固结,限定三个方向的位移及转角,取UR1=U R2=UR3=U1=U2=U3=0;将两个边支座设置为铰结,限定Y轴、Z轴的位移及X轴、Z轴的转角,取U2=U3=UR1=U R3=0,同时采用位移加载模式进行有限元分析。连续梁E2的模型如图2所示。

图2 E2有限元模型Fig.2 Finite element model of E2
1.3 有限元模拟分析与验证
图3 为提取模型中的数据得到的荷载-跨中位移曲线与文献[15]中的相应曲线的对比。表2进一步给出了各试验梁的关键荷载及位移。文献[15]中未给出试验屈服荷载及屈服位移,故表2也未给出具体数据。
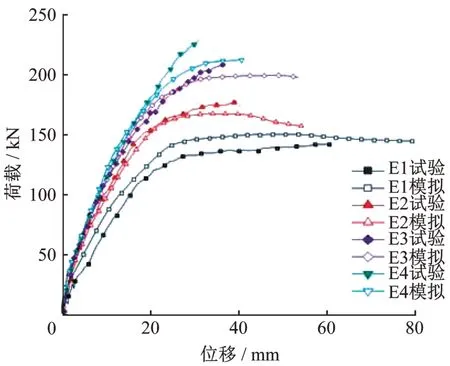
图3 荷载-跨中位移曲线对比Fig.3 Comparison of load-deflection
由表2可见,CFRP加固连续梁E2、E3、E4与参考连续梁E1相比,位移延性系数减小,模拟的屈服荷载及极限荷载均有提高;模拟的极限荷载值与试验较接近。
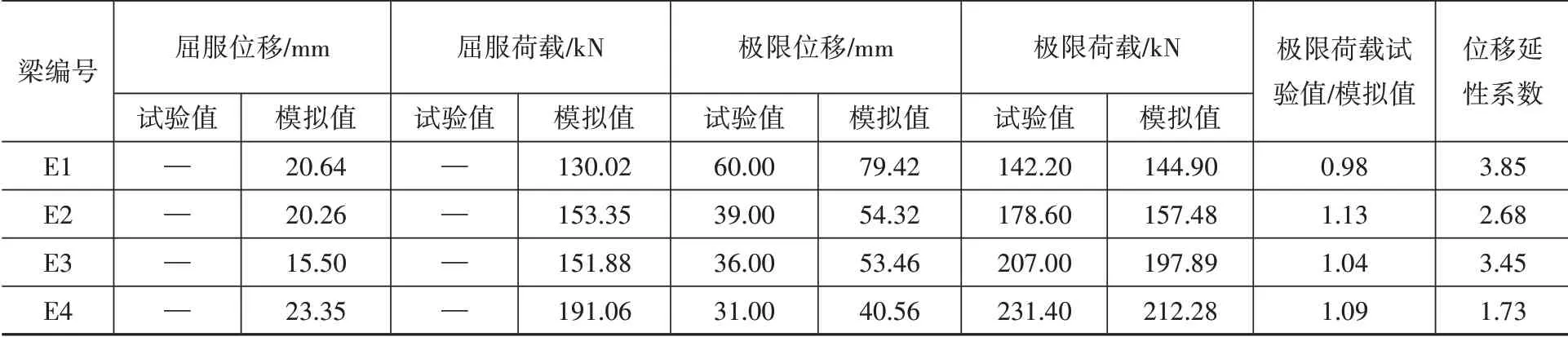
表2 连续梁主要模拟值与试验结果对比Table 2 Comparison between test results and finite element results
结合图3及表2可见,梁E1-E4的荷载-跨中位移曲线在钢筋屈服前与试验基本吻合,在屈服至极限阶段存在一定差异。这些差异出现的原因如下:有限元模拟中的支座约束与真实支座约束存在偏差;模型中混凝土等材料的本构与实际材料的本构有一定差异。综上,若能确保模拟支座约束与实际一致,材料本构保持一致,则应用ABAQUS软件对CFRP加固双跨连续梁进行模拟是切实可行的。
由图表进一步分析可知,用CFRP加固连续梁能有效地增加梁的抗弯承载力,同时加固连续梁的延性均有一定程度的下降。连续梁的弯矩重分布程度越大则表明塑性铰转动能力越强。塑性铰转动能力越强表明梁延性越好。若明确CFRP加固钢筋混凝土连续梁的弯矩重分布,并将其应用于设计中,就可以较为真实地判断结构的承载能力。因此,在试验研究有限的情况下,有必要通过已验证的有限元模型进一步研究CFRP加固钢筋混凝土连续梁抗弯性能及弯矩重分布特征。
2 加固连续梁抗弯性能的影响参数分析
影响外贴CFRP加固钢筋混凝土连续梁抗弯性能的主要因素有CFRP加固量、加固位置、黏结长度及CFRP力学性能等。现有研究[5]主要分析了CFRP加固量及其力学性能对加固梁性能的影响,本文拟从改变FRP黏结长度及加固位置的角度,研究其对FRP加固RC连续梁的抗弯性能的影响。
2.1 CFRP黏结长度对负弯矩区加固连续梁的影响
本文以有限元模型E2梁为基础,保持其他建模参数不变,仅改变CFRP黏结长度,建立了多根负弯矩区加固梁的有限元模型,并定义CFRP黏结长度与梁跨度之比为α1。
表3为不同α1下负弯矩区加固连续梁的主要计算结果及位移延性系数。由表3可得,加固连续梁的屈服荷载随着α1的增加非线性增加;α1≤0.4时,极限荷载随着α1的增加而增加,α1>0.4时,极限荷载基本不变。相比于未加固梁E1,各梁屈服荷载的增幅在9.54%~18.60%之间,极限荷载增幅在6.96%~11.42%之间。同时梁的位移延性系数基本上随着α1的增大而减小。综上,当α1=0.4时,负弯矩区加固梁既能获得较强的承载能力也兼顾了良好的延性。
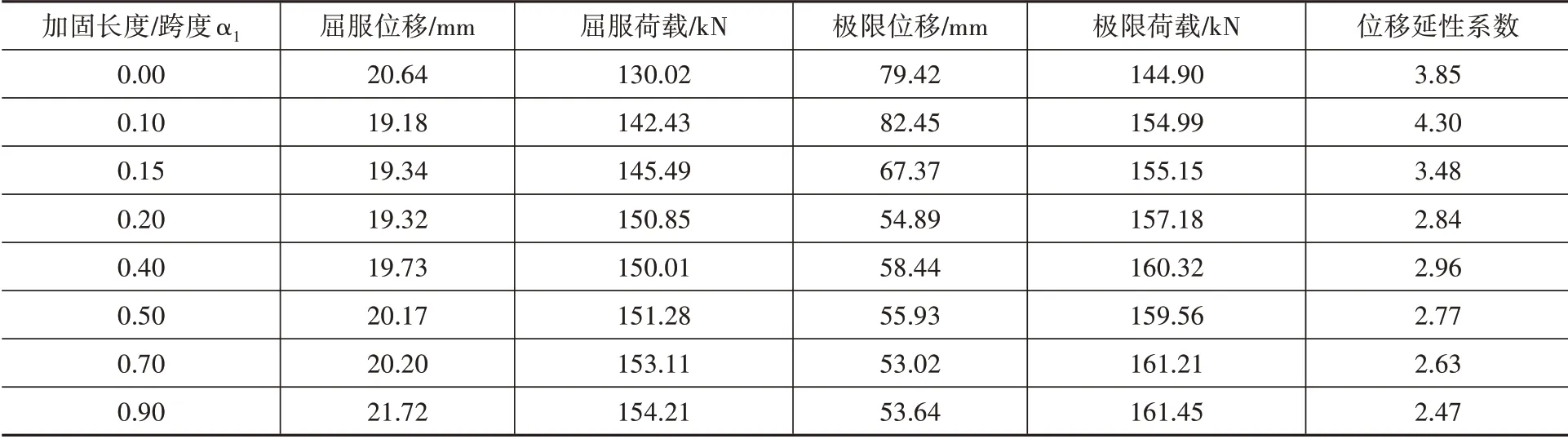
表3 负弯矩区加固主要计算结果Table 3 Main calculation results of beams strengthened in negative moment
2.2 CFRP黏结长度对正弯矩区加固连续梁的影响
本文以有限元模型E3梁为基础,保持其他建模参数不变,仅改变CFRP黏结长度,建立了多根正弯矩区加固梁的有限元模型,并定义CFRP黏结长度与梁跨度之比为α2,研究α2对加固梁抗弯性能的影响。表4为不同α2下加固连续梁的主要结果及位移延性系数。

表4 正弯矩区加固主要计算结果Table 4 Main calculation results of beams strengthened in positive moment
由表4可知,从承载力来看,正弯矩区加固连续梁的屈服荷载随着α2的增加而增加;在α2≤0.6时极限荷载随着α2的增加而增加,当α2>0.6后极限荷载较为稳定。与未加固梁E1相比,屈服荷载增幅在3.80%~17.94%之间,极限荷载增幅在16.05%~36.79%之间。从变形性能角度上来看,随着α2的增加,梁达到极限状态时的位移延性系数一直减小。故可知,正弯矩区加固连续梁的CFRP粘贴长度与梁跨度的最优比值α2为0.6。
3 弯矩重分布研究
连续梁的内力重分布大致分成两段,第一段是混凝土截面开裂至形成塑性铰;第二段是塑性铰形成后到结构处于极限状态。在这两个阶段中,连续梁的内力重分布集中在第二段。基于以上的理论,本文主要探讨第二段的内力重分布。
世界各国研究人员提出许多探究连续梁内力重分布的方法,如塑性铰法、全过程分析法、变刚度法及弯矩调幅法等。塑性铰法及变刚度法假定过多;全过程分析法计算过程过于复杂;弯矩调幅法因其思路清晰、计算简洁而被各国采纳。弯矩调幅法是以弹性方法得到的弯矩值按弯矩重分布能力进行适当调整,弯矩重分布能力大小用弯矩调幅系数β来表示,β按下式确定:

式中:MT为有限元分析得到的弯矩值;Me为弹性方法计算的弯矩值。其中梁的实测弯矩由模型提取,弹性弯矩值由力法计算。
表5为在不同α1下负弯矩区加固梁达到极限状态时的弯矩调幅系数。由表5可知,随着α1的增加,负弯矩区加固梁的跨中弯矩调幅系数β1及中支座弯矩调幅系数β2均逐渐减小,其中β1降幅在-0.04~-0.17之间,β2降幅在0.07~0.29之间。在α1达到最优值0.4后,β1与β2基本保持不变。
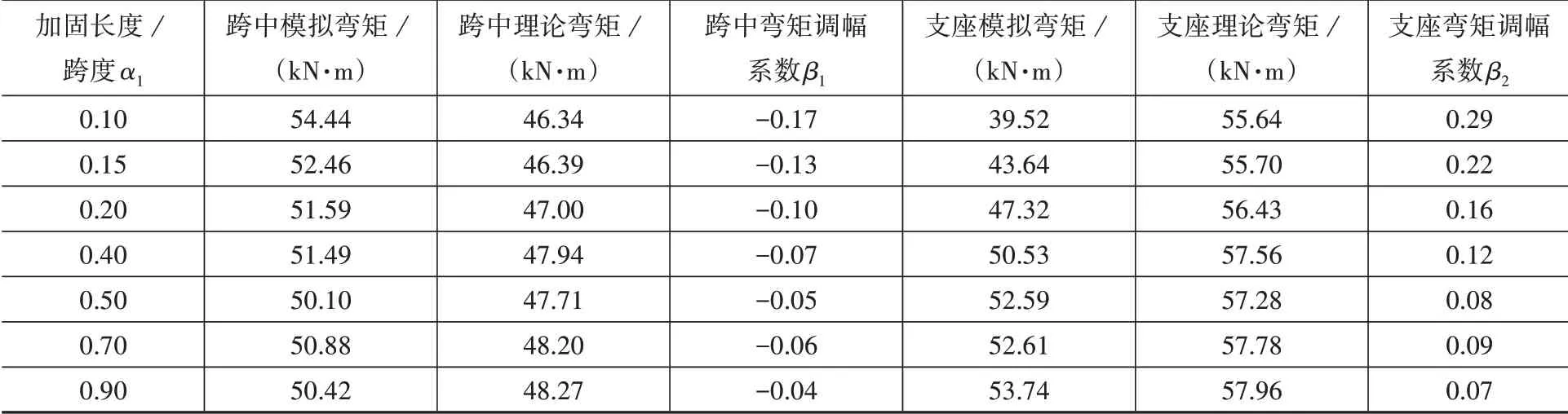
表5 不同α1时极限状态下关键弯矩值Table 5 key bending moment values in limit state under differentα1
基于以上分析,将负弯矩区加固梁的α1~β1及α1~β2的试验点分成两段,第一段α1≤0.5,第二段α1>0.5。以α1为横坐标,以β1,β2为纵坐标,可以得到负弯矩区加固梁的第一段试验点分布,如图4所示。
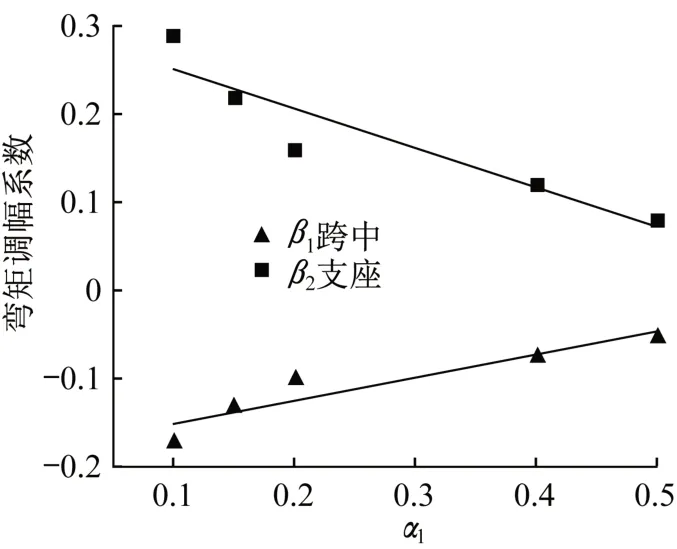
图4 α1~β1及α1~β2拟合曲线Fig.4 Fitting curve ofα1~β1 andα1~β2
经拟合之后得到以α1为自变量的负弯矩区加固梁达到极限状态下的β1的公式:
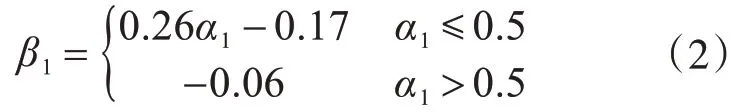
上述拟合公式中相关系数R2为0.88。
以α1为自变量的负弯矩区加固梁达到极限状态下的β2的公式:
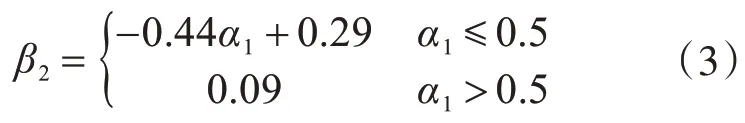
上述拟合公式中相关系数R2为0.86。
由表5可见,负弯矩区加固梁的第二段弯矩调幅系数β1或β2均随着CFRP黏结长度的增加基本不变,即为恒定值。
表6为正弯矩区加固梁在不同α2下达到极限状态时的弯矩调幅系数。由表6可知,随着α2的增加,正弯矩区加固梁的跨中弯矩调幅系数β3及中支座弯矩调幅系数β4基本逐渐增大,其中β3增幅在-0.08~-0.17之间,β4增幅在0.13~0.28之间。在α2达到最优比值0.6后,β3与β4基本保持不变。
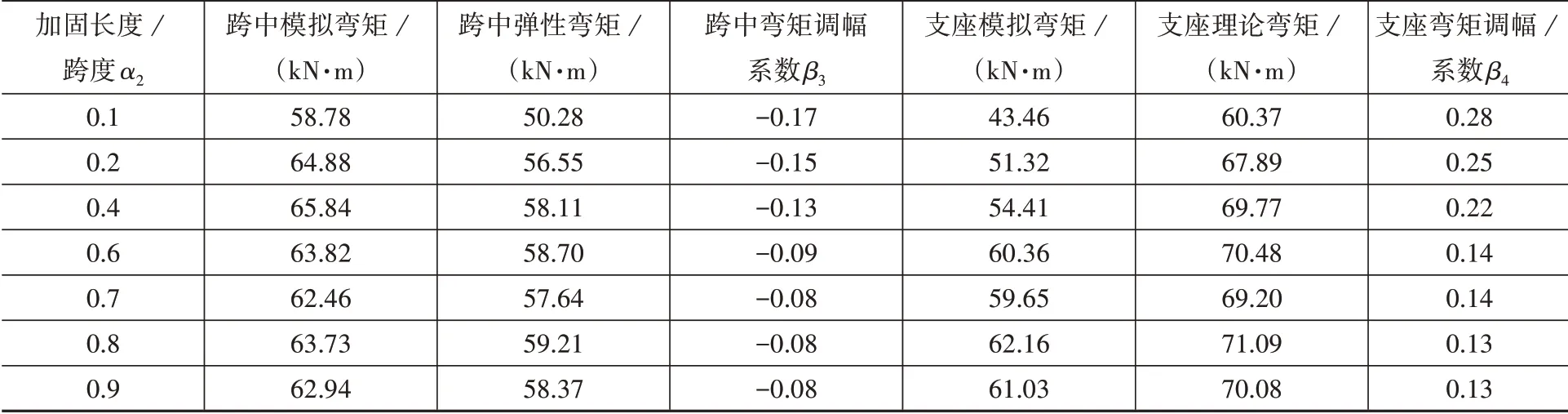
表6 不同α2时极限状态下模拟弯矩值和理论弯矩值Table 6 Key bending moment values in limit state under differentα2
将正弯矩区加固梁的α2~β3及α2~β4的试验点分成两段,第一段α2≤0.7,第二段α2>0.7。图5为以α2为横坐标,以β3,β4为纵坐标,得到的第一段正弯矩区加固梁α2~β3及α2~β4的试验点分布。
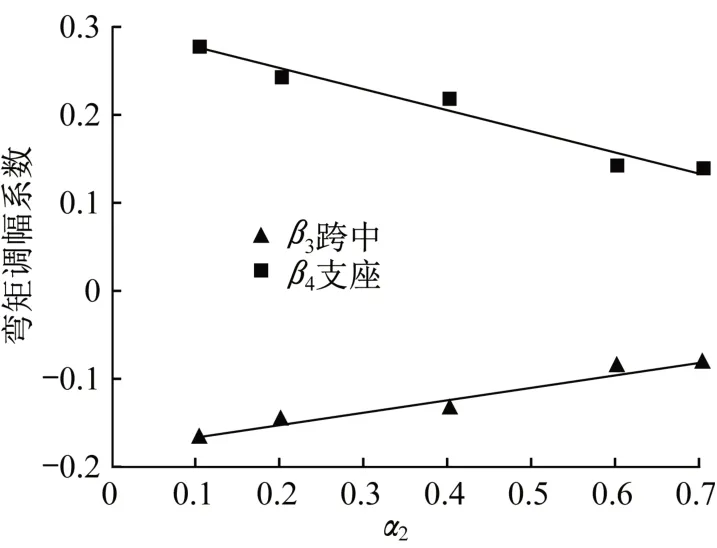
图5 α2~β3及α2~β4拟合曲线Fig.5 Fitting curves ofα2~β3 andα2~β4
经拟合之后得到以α2为自变量的正弯矩区加固梁达到极限状态下的β3的公式:
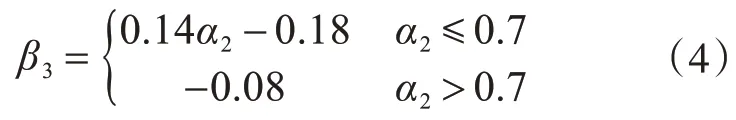
上述拟合公式中相关系数R2=0.96。
以α2为自变量的正弯矩区加固梁达到极限状态下的β4的公式:
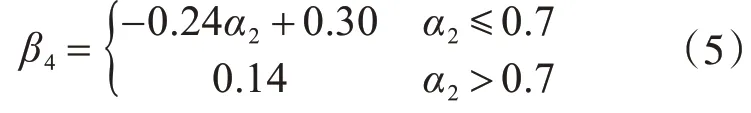
上述拟合公式中相关系数R2为0.96。
由表6可见,负弯矩区加固梁的第二段弯矩调幅系数β3或β4均随着CFRP黏结长度的增加基本不变,即为恒定值。
综上,负弯矩区加固梁的最优比值α1为0.4,建议极限状态下跨中弯矩调幅系数β1按式(2)取值,中支座弯矩调幅系数β2按式(3)取值;正弯矩区加固梁的最优比值α2为0.6,建议极限状态下跨中弯矩调幅系数β3按式(4)取值,中支座弯矩调幅系数β4按式(5)取值。
4 公式的应用及正确性验证
为了进一步说明公式的应用及正确性,本文对公式进行了应用说明,并收集了国内外外贴CFRP加固RC连续梁的试验数据,将试验弯矩与调幅后的弯矩进行对比,以验证公式的正确性。
表7、表8分别为负弯矩区及正弯矩区加固RC连续梁的关键数据,其中ME1为调幅后的跨中弯矩,MT1为跨中试验弯矩;ME2为调幅后的中支座弯矩,MT2为中支座试验弯矩。限于篇幅,表7、表8仅利用文献[10]、[17]的试验数据进行验证分析。
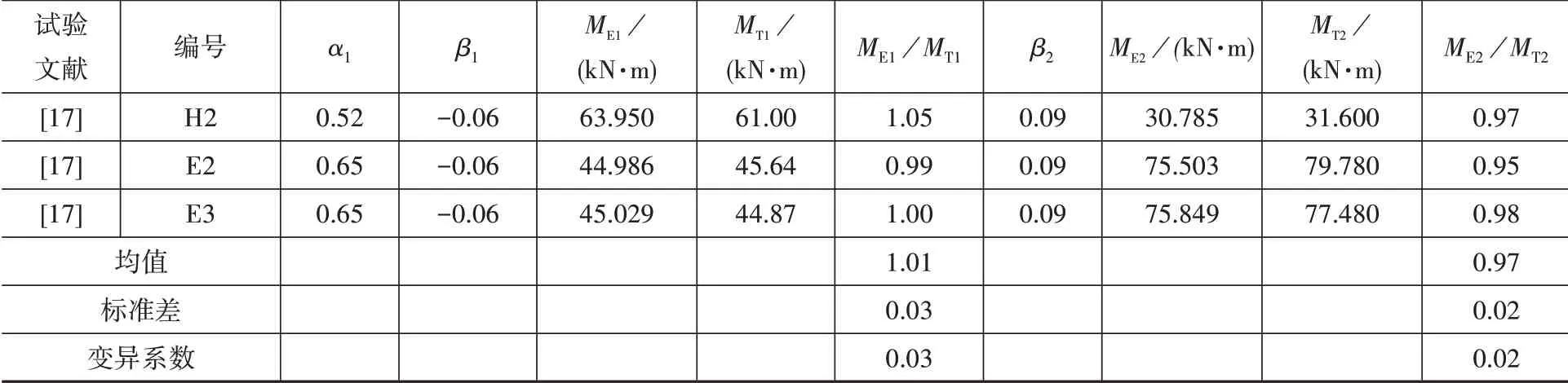
表7 负弯矩区加固梁弯矩计算值与试验值对比Table 7 Comparison between calculated moment and test moment of negative strengthened beam
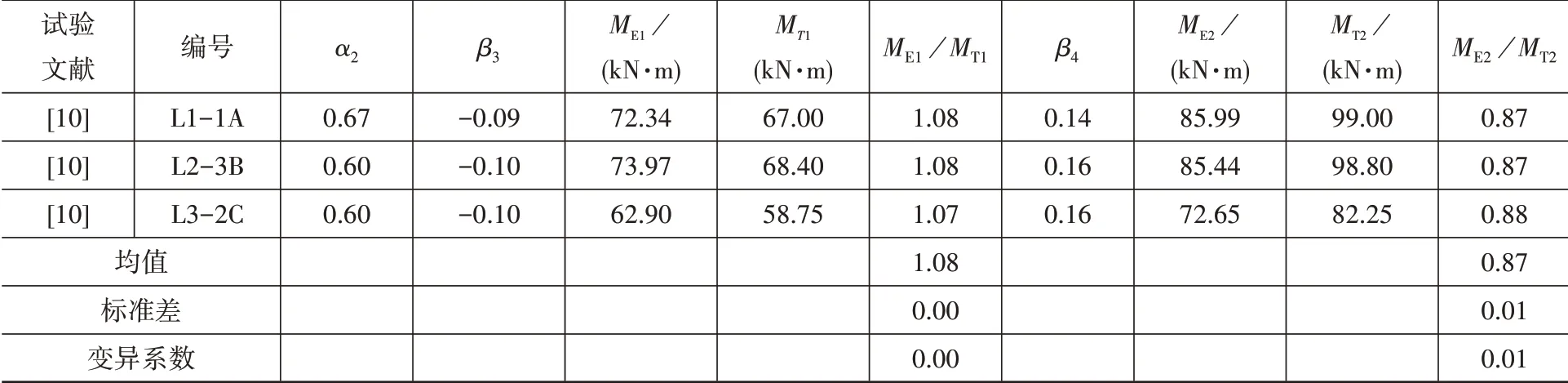
表8 正弯矩区加固梁弯矩计算值与试验值对比Table 8 Comparison between calculated moment and test moment of positive strengthened beam
ME1的计算过程如下:首先由规范算出跨中理论弯矩Me1;其次根据试验梁的实际情况算出黏结长度与跨度的比值;再根据比值套用本文拟合的公式,得出弯矩调幅系数;最后由弯矩调幅系数及跨中理论弯矩Me1得出ME1。经调幅后的中支座弯矩同理。
表7中的ME1及ME2由以上方法计算而来;Me1、Me2、MT1、MT2取自文献[17];表8中的Me1、Me2由力学方法计算而来,ME1及ME2根据以上方法计算,MT1、MT2由文献[10]中的支座反力与相应跨度相乘而来。
从表7及表8可见,虽经调幅后的弯矩与试验弯矩相比有一定误差,但最大误差不超过13%,仍在可接受范围之内。故可得经调幅后的弯矩与试验弯矩较吻合,即本文所拟合的公式具有一定的参考价值。
5 结 论
本文完成了外贴CFRP加固RC连续梁抗弯性能参数影响分析,提出了连续梁极限状态时跨中及中支座弯矩调幅系数随CFRP黏结长度与梁跨度比值变化的公式并进行验证,得到主要结论如下:
(1)建立了外贴CFRP加固RC连续梁的有限元模型;数值分析结果表明:连续梁的屈服荷载随着CFRP黏结长度的增加而增加,极限荷载随着CFRP长度的增加先增加后基本不变,位移延性系数随着CFRP长度的增加而减小。
(2)在简化的基础上,本文建议负弯矩区加固梁中CFRP黏结长度与梁跨度最优比值α1为0.4,正弯矩区加固梁中CFRP黏结长度与梁跨度最优比值α2为0.6;
(3)本文分别提出了负弯矩区加固连续梁中CFRP黏结长度与梁跨度之比α1和弯矩调幅系数β1、β2的关系公式及正弯矩区加固连续梁中CFRP黏结长度与梁跨度之比α2和弯矩调幅系数β3、β4的关系公式。通过试验数据验证分析,表明本文拟合的公式具有一定的参考价值。

