Kalman滤波组合预测模型研究及其在高铁路基沉降中的应用

焦雄风 张献州 蒋英豪 陈 铮 谭社会

(1.西南交通大学地球科学与环境工程学院,成都 611756; 2.高速铁路运营安全空间信息技术国家地方联合工程实验室,成都 611756; 3.中国铁路上海局集团有限公司,上海 200071)

1 概述

影响高速铁路路基沉降的因素较多,建立各影响因素与形变过程之间精确的函数模型十分关键。已有许多学者开展相关研究,毛文飞等研究了改进的MEEMD-ARMA残差修正组合预测模型[1];岳春芳等将RBF神经网络组合模型应用于GPS高程拟合中[2];杨帆等研究自回归预测模型变权组合定阶方法[3]。上述研究表明,组合预测模型不论是从信息丰度还是预测效果方面都优于单类预测模型。然而,在每一次预测计算时,需要根据往期先验信息重新调权,会造成大量计算冗余。近年来,自适应Kalman滤波理论趋于成熟,冯磊等研究自适应Kalman滤波在高铁沉降观测数据处理中的应用[4];Christopher等将自适应Kalman滤波应用于INS/GPS的组合导航中[5];Akbar等基于协方差采样提出一种自适应卡尔曼滤波模型,并验证了该方法的有效性[6]。基于前人的研究,采用基于极大似然估计的自适应Kalman滤波算法与组合预测模型进行结合,与目前较为实用的预测模型进行比较,从拟合情况、精度评判指标等方面,探究上述自适应kalman滤波组合预测模型的可靠性。

2 单类因素预测模型构建

2.1 单类因素预测模型容量选择

研究表明,并不是囊括越多单类因素预测模型,其组合预测模型的精度就越好[7]。相反,如果构建的单类预测模型精度不高,甚至与其他单类预测模型发生信息冲突,还会降低组合预测模型的精度。为了解决上述问题,尝试采用包容性检验原理[8]来处理组合预测模型的容量选择问题,步骤如下。

假设w1、w2为两种不同的单类预测模型,两者第t期的预测值为δ1,t、δ2,t,当期实际变化量为γt时,可表示为

Φ1、Φ2分别表示回归系数,且两者之和为1,ut为方程随机噪声。

上式同时减去δ1,t,有

设εi,t=γt-δi,t(i=1,2),则有

由此,组合预测模型的容量选择问题可看作对式(3)的线性假设的显著性检验, 给出假设

(3)当Φ1=0,Φ2=1时,则表示w2包容w1,即w2包含w1的信息,w1对组合预测模型没有影响,可裁去w1;当Φ2=0,Φ1=1时,则表示w1包容w2,即w1包含w2的信息,w2对组合预测模型没有影响,可裁去w2。

当单类预测模型推广到n个时[9],可将其看作第i类单类预测模型和n-i个单类预测模型的集合,首先对单类预测模型进行预测精度评价,然后对其预测效果进行排序,基于上述两种单类预测模型包容性检验的思想,对单类预测模型逐个检验,最后得到1组效果最优的组合预测模型。

2.2 单类因素预模型定权

建立组合预测模型正确与否取决于两大核心问题:①单类模型的正确选择;②单类预测模型的权重。针对第二点,采用熵值法进行权重赋予。

利用熵值法对单类预测模型赋权,λit为单类预测模型相对误差,有

αit表示t期第i类预测模型的预测相对误差值,其取值如下

3 改进Kalman滤波

3.1 基于极大似然估计的自适应Kalman滤波

标准Kalman滤波函数模型为:

其中,xk为(n×1)初值参数矩阵;zk为(m×1)监测参数矩阵;wk为(n×1)动态噪声;vk为(m×1)监测噪声;Φk/k-1为(n×n)状态转移矩阵;Hk为(m×n)观测矩阵;Bk/k-1为(n×r)控制参数的增益矩阵;uk-1为(r×1)控制参数矩阵;下标k为第k时刻在某一时刻的估值,可按如下公式递推演算得到。

状态值及估计协方差矩阵一步预测为

测量误差、测量误差协方差及最优卡尔曼增益一步更新为

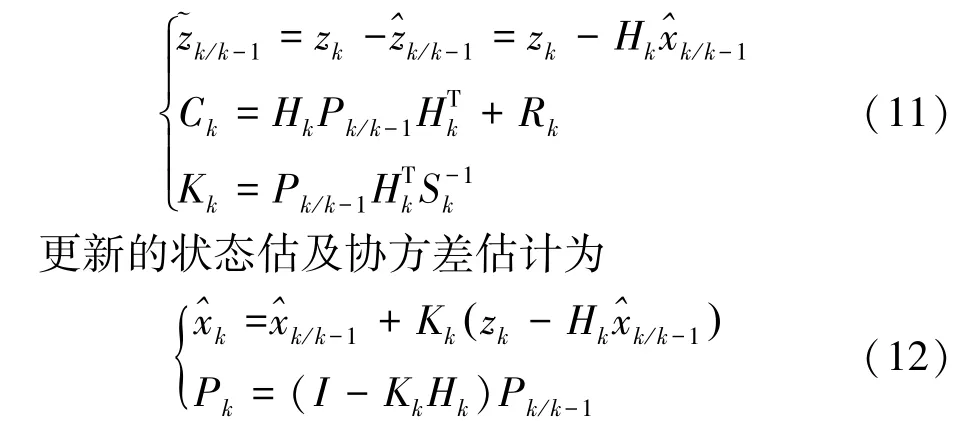
通过上述公式递推流程,若给定初值状态参数以及在k时刻下的观测值Zk,就能得到在k时刻下目标状态的一步预报值

上述标准Kalman滤波中的Q和R都为固定参数,无法随着预测误差的变化动态调整,有学者提出一种基于极大似然估计理论的自适应Kalman滤波[10],从系统测量出现概率最大的方面来预测,不但可以追踪预测误差变化,还可以捕捉预测误差的协方阵变化[11]。其自适应性体现在系统噪声协方差阵Q和观测噪声协方差阵R的实时修正[12],主要通过基于预测

式中,tr表示对矩阵求逆。由此,对Q、R的修正问题转变为对参数α求导的问题。

根据标准Kalman滤波基本方程,有

假设滤波处于稳态时,状态误差的方差阵Pk-1理论上无限接近某常量,有

通过上述公式,可以求得α的实时估计,进而可以对Q、R进行实时修正。

3.2 噪声协方差矩阵的几种修正方式

(1)测量噪声协方差矩R修正

假设系统噪声协方差阵Q已知,式(20)可以简化为

(3)噪声协方差阵Q、R同步修正

通过上述修正方式可以看到,当对其中1个噪声协方差阵进行调整时,必须假设另1个为已知量,即两者必须有1个作为已知量。同步调整2个噪声协方差阵时,若不考虑已知信息,则可能导致式(21)、式(24)不成立[15],继而导致滤波稳态丧失,达不到所要求的自适应性。故应慎重考虑同时对Q、R的同步修正。

4 基于极大似然估计的自适应Kalman滤波组合预测模型

4.1 组合预测模型建立

一般情况下,对同一观测值,假设用m种单类预测模型预测,其组合预测模型为

例如某种变形量与温度、时间因子的组合预测模型[16],有

式(29)、式(30)建立后,即可用基于极大似然估计的自适应Kalman滤波算法进行推算。

4.2 模型预测精度评价指标

引入Pearson相关系数、相关指数R2、均方根误差RMSE[17]、平均绝对误差MAE来进行相关性分析及模型预测精度评价,pearson能衡量两变量之间是否存在线性相关关系,其值越接近1,表示两者相关性越强;R2能衡量模型回归效果,其值越接近1,表示回归效果越显著;RMSE能反映估值与监测值之间的偏差,其值越小表明其模型预测精度越好;MAE能反映估值误差的实际情况,其值越小,表明模型拟合程度越高,公式为

式中,m为观测期数;表示模型估计值表示观测量平均值;yi、xi表示实际观测量。

5 实例分析

5.1 高速铁路路基沉降监测数据分析

(1)工程概况

某高速铁路路基区段,长1.916km,共26个观测断面,每个观测断面在上下行各设1个路基观测桩进行监测,路基填筑完成时间为2018年12月31日,利用高精度水准仪及精密水准尺进行若干次的周期性重复测量,监测内外业精度均符合相关规定。

(2) 数据分析

现对该路基的小里程段、中里程段、大里段各挑选1个观测断面,选取2016年6月至2019年12月对应的上行路基观测桩 0085880L1、0086686L1、0087492L1监测数据(共180期)进行分析,数据如图1所示。

由图1可知,3个断面路基观测桩的监测数据都表现为逐渐沉降且趋于稳定。

图1 累计沉降监测数据

路基沉降主要受外力荷载的影响,堆载预压都会使路基随时间发生一定程度的沉降。另外,还需要考虑荷载作用次数及地质类型等,这类参数因子难以量化,而通过路基填筑平均高度及时间的变化来建立路基沉降预测模型,可定量分析具体沉降趋势。

5.2 单类预测模型建立

路基沉降拟合预测常用方法有双曲线法、三点法、泊松曲线法等,这些方法均考虑以时间因子为自变量,累计沉降量为因变量,即沉降随时间发生变化。因此,根据上述3个监测桩的沉降趋势,提出6种以时间因子为自变量的预测模型,有

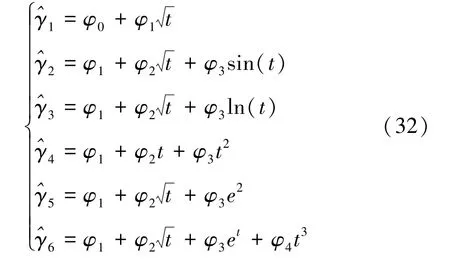
式中,分别表示基于时间因子的模型预测值;t为以天为单位数值化的时间因子;φi表示模型回归参数。

为筛选出最优预测模型,以前120期的监测数据为建模样本,预测后一期的累计沉降量,有关精度分析情况如图2、表1所示。

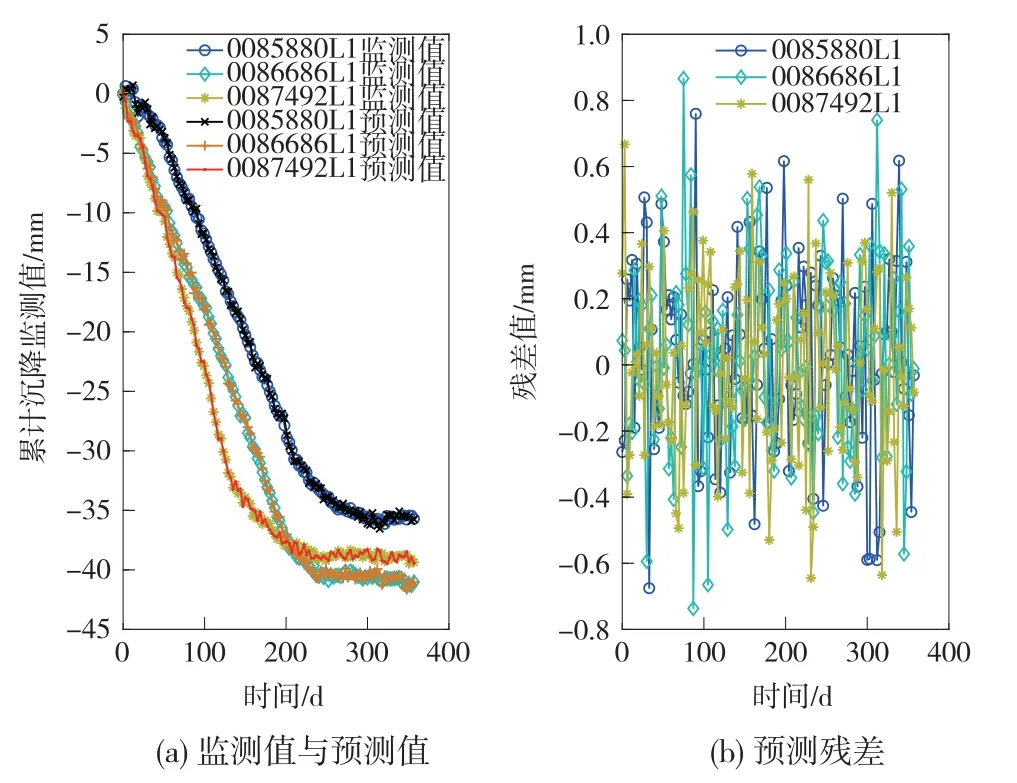
图2 基于时间因子的单类模型预测结果及残差

表1 精度评价指标

为判断路基填筑平均高度与路基桩沉降是否具有强相关性,取监测当日、前15d、前30d和前45d的路基填筑平均高度与当日路基观测桩沉降量的pearson相关系数,如表2所示。

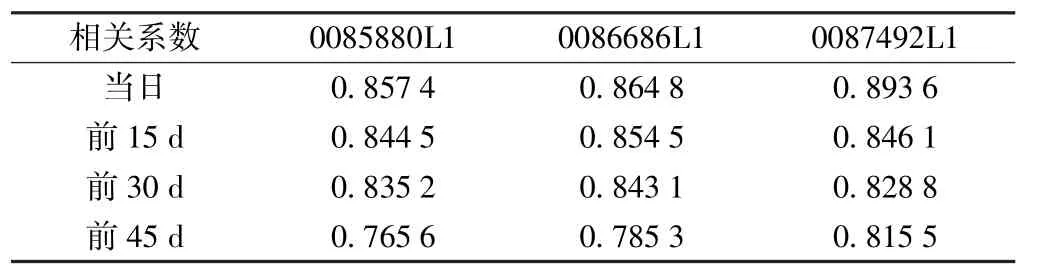
表2 pearson相关系数

由表2可知,该段路基填筑平均高度变化与路基桩沉降量存在强线性相关。取监测当日、前15d、前30d、前45d的路基填筑平均高度作为自变量,预先构建线性模型,有

式中,分别表示基于路基填筑平均高度的模型预测值,μi表示回归参数。θi表示监测当日的前i天的路基填筑平均高度。

选择与基于时间因子预测模型同样的数据进行计算,结果如图3、表3所示。

表3 精度评价指标

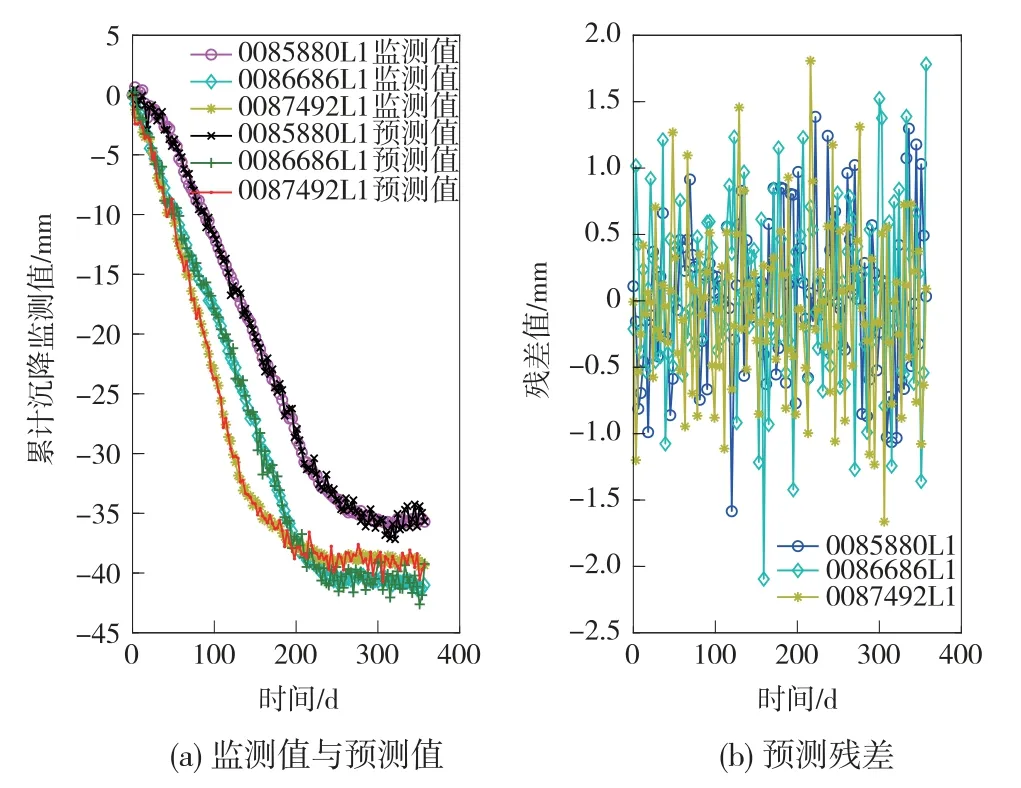
图3 基于路基填筑平均高度的单类模型预测结果及残差

确定上述单类预测模型具体参数后,利用2.1节的包容性检验原理对两个单类预测模型之间的信息包含程度进行分析,取显著性水平α=0.025,经计算,3个点0085880L1、0086686L1、0087492L1的t统计量分别为4.054、4.5823、4.2359,由此可见,t0.0025(58)=2.0017,原假设不成立,即单类预测模型可组合。

组合预测中的单类预测模型容量确定后,再利用熵值法对两单类预测模型进行定权,取第前119期的两单类预测数据作为计算数据,求得120期数据的各单类模型权值,结果如表4所示。

表4 单类模型权值分配情况

5.3 模型预测分析

当上述组合预测模型确定后,即可利用基于极大似然估计的自适应Kalman滤波进行滤波推估,取组合预测模型第120期的预测模型参数为状态参数初值,取初始估计协方差矩阵P0为I(单位矩阵),考虑组合预测系统的估计误差,采用2.3节的第二种方差调整方式进行自适应调整,系统噪声协方差矩阵Q=1、观测噪声协方差矩阵取R=0.01,为对所提出组合预测方法性能进行客观评价,增加基于非等间隔灰色系统的最优权组合预测模型进行对比实验,计算结果及精度评价如图4、表5所示。

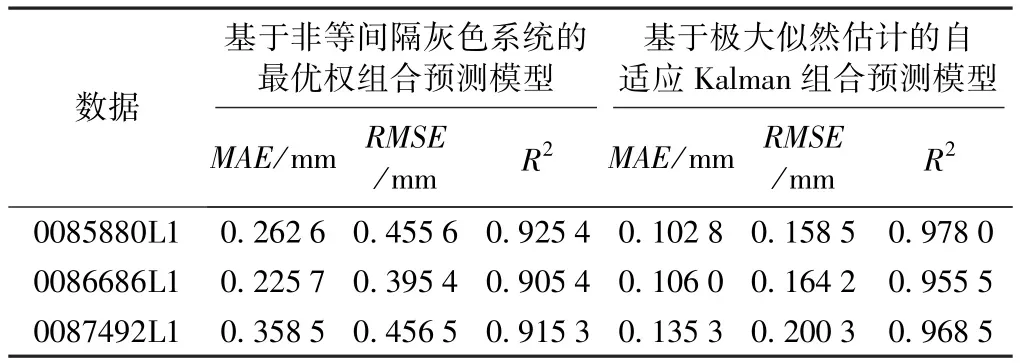
表5 精度评价指标

由图4、表5可知,基于非等间隔灰色系统的最优权组合预测模型的平均绝对误差、均方根误差、相关指数最优精度分别为0.2257mm、0.3954mm、0.9254;基于极大似然估计的自适应Kalman组合预测模型的平均绝对误差、均方根误差、相关指数最优精度分别为0.1028mm、0.1585mm、0.9780。实验表明,基于极大似然估计的自适应Kalman组合预测模型各项精度指标皆优于基于非等间隔灰色系统的最优权组合预测模型。由此可见,在对单类预测模型加权组合后,其预测精度得到了提高,而结合自适应Kalman滤波,可进一步增强组合预测模型的自适应性。

图4 两种预测模型预测残差

6 结语

建立组合预测模型来分析高速铁路路基沉降监测数据十分必要,上述研究表明,组合预测手段能在一定程度上改善预测精度,结合基于极大似然估计的自适应Kalman滤波算法,利用其只需一定的初始参数,就能自动更新迭代,且在更新的过程中不断对噪声方差进行修正的自适应特性,可解决组合预测模型中冗余计算等问题,有效减少组合预测模型误差的积累,提高组合预测模型的自适应能力。但上述模型只考虑2种单类预测模型的组合问题,而现实中其他环境因素的并没有考虑,需要进行深入研究。