涵道式垂直起降固定翼无人机纵向稳定性研究

王春阳, 周洲, 王睿, 王科雷

(西北工业大学 航空学院, 陕西 西安 710072)

涵道式垂直起降固定翼无人机是一种复合型无人机，它既有直升机的垂直起降、空中悬停、低空低速飞行性能，又有固定翼飞机的高度巡航性能，它兼具了直升机和固定翼飞机的优点，是无人机发展的一个方向。它优异的性能和良好的经济性在军事领域和民用领域都有重要作用，具有广阔的发展前景[1]。

涵道式垂直起降无人机有3种飞行状态：起降悬停状态、水平飞行状态和过渡飞行状态。为了满足垂直起降和水平飞行，又能在两者之间进行过渡飞行的要求，其自身过渡的稳定性问题就必须解决。由于过渡过程中飞行器构型不断变化，为实现平稳过渡，各种动力单元共同参与，此时必须考虑过渡转换过程中合理的动力分配、合理的速度范围，保证无人机升力满足飞行需求，以及过渡过程中动力单元和飞行姿态是连续变化的，因此过渡飞行状态是垂直起降无人机最复杂的飞行状态。为保证过渡飞行安全就必须确定飞机的过渡飞行走廊和飞行稳定性，使得飞行器在过渡走廊内安全过渡飞行。此外，建立这种涵道式飞行器动力部件的数学模型和整机的动力学模型时，如何准确地描述其过渡飞行运动，也是该类飞行器研究的重点。

涵道式飞行器有着特殊的构型，由于设计方案普遍动力配置充足，在过渡稳定性方面有较少的研究。在垂直起降方面，诸多学者进行了研究，包括气动特性计算、动力学建模、飞行性能等方面。Leishman和Ananthan对共轴双旋翼升力风扇进行了理论计算模型研究，运用叶素动量理论建立了共轴对转双旋翼的气动力计算模型，通过理论模型研究了共轴对转风扇的上下转子的最佳叶片匹配[2]。郑志成等参考涵道风扇动量理论模型, 建立了针对垂直起降飞机总体设计中关于升力风扇的估算模型，并通过具体算例对其进行验证[3]。Yuksek等建立了升力风扇式垂直起降无人机六自由度非线性方程，并根据建立的数学模型进行了仿真计算模拟[4]。史小明以倾转旋翼飞行器为研究对象，对其进行了纵向的飞行器建模，建立了飞行器气动部件的气动模型，并根据建立的纵向模型进行了配平和过渡阶段稳定性分析[5]。曹芸芸以倾转旋翼飞行器为对象，研究了倾转走廊包线的确定方法，建立了动力学模型，根据模型对案例进行了分析计算，并根据飞行器特点研究了倾转旋翼的操纵策略以满足悬停和小速度飞行和过渡飞行模式[6]。万华芳建立了倾转旋翼飞行器的动力学理论模型，对过渡走廊进行了仿真研究[7]。高阳等对垂直/短距起降飞机进行了非线性动力学模型的建模[8]。符大伟等对升力风扇系统进行了较为详细的实时数学模型建模[9]。此类研究注重倾转旋翼类飞行器和升力风扇类飞行器的动力学建模和过渡走廊研究，本文将针对涵道式垂直起降无人机进行动力部件基于实验数据的动力建模和全机动力学建模以及纵向稳定性研究。

1 涵道式垂直起降固定翼无人机

此类垂直起降无人机动力系统由共轴对转升力风扇和推力涵道组成，升力风扇位于机体重心之前，推力涵道位于机翼后缘。垂直起降无人机主要气动部件包括对转升力风扇、左右增升涵道、左右控制 翼面和主机翼。文中整机的气动力建模采用机体轴系OXbYbZb,如图1所示,该轴系的原点位于飞行器的重心,x轴沿机体构造对称面指向前,y轴垂直于x轴向右,z轴由右手法则确定向下,x轴与z轴构成了机体的对称面[10]。气动部件建模以气动部件体轴系为基准。

图1 涵道式无人机坐标系

方案无人机从起飞悬停到过渡飞行过程如图2所示,其中垂直起降时通过涵道偏转提供向上的推力与前方的升力风扇一同产生推力使得无人机能够垂直起降;过渡过程中通过偏转涵道倾角来获得前飞的推力,在一定的控制策略下能过完成从垂直起飞到水平飞行的过渡;在水平飞行时,涵道偏转至水平,通过控制舵面的偏转来控制飞行姿态。

图2 不同飞行状态的涵道偏转

2 气动部件建模

涵道螺旋桨与孤立螺旋桨相比,在相同功率下,相同桨盘直径时，可产生较大的拉力,即在相同功率下,产生相同拉力所需直径更小。涵道螺旋桨产生这种差异的机理是:

1) 涵道的存在改变了螺旋桨下游的滑流状态,增大了滑流面积,减小了滑流速度和滑流动能损失,从而较多地将螺旋桨桨盘后的动能转化为压力能。

2) 涵道壁面改善了螺旋桨桨尖区域的扰流特性,减少了扰流损失。

3) 涵道的入口前缘形成较大的负压区,产生附加拉力。

共轴对转升力风扇是由一对螺旋桨组成,上下分布,绕同一根轴转动,但是旋转方向相反。共轴对转桨有以下优点:

1) 共轴对转,使得发动机传给飞机的反作用力矩减小到零。

2) 在最大飞行速度Vmax状态下,共轴螺旋桨的总效率要比其总叶数目相等、飞行条件(来流速度V0,螺距H,转数n,桨叶数N和桨半径D)相同的非共轴螺旋桨效率高。

3) 高速飞行时,共轴螺旋桨的效率比具有相同任务的2个孤立螺旋桨效率高。

4) 共轴螺旋桨的起飞性能(在原地的拉力)要比单独螺旋桨要好[11]。

目前尚无带涵道的共轴双旋翼空气动力理论可供参考,本文基于共轴双旋翼数学模型的计算数据和实验数据,通过引入涵道唇口拉力修正系数η的方式,给出共轴双旋翼涵道风扇的动力学模型。

2.1 升力风扇气动力模型

本文采用叶素动量理论(blade-element moment theory,BEMT)[12]计算共轴双旋翼的升力、功率以及力矩,由于文中飞行稳定性侧重于升力和力矩,而对转桨升力风扇力矩基本可以相互抵消,所以气动力部件建模重点为升力的建模。计算公式采用NASA提出的无量纲形式[11]:

T=ρA(ΩR)2CT

(1)

共轴对转双旋翼系统的流动模型如图3所示。基本假设是下旋翼部分桨盘面积工作在上旋翼的尾流区域,并且上旋翼尾流在进入下旋翼桨盘之前滑流速度在颈缩截面处有一个大的改变。尾流的收缩基于理想流体流动假设,或者通过特定的实验数据支持。

图3 共轴对转旋翼叶素动量理论分析模型

BEMT模型假设是上旋翼的滑流(流出)影响了下旋翼的滑流(流入),而下旋翼不会对上旋翼产生诱导影响。叶素动量理论可以用轴向自由来流速度进行一般性地推广,自由来流速度一般记为V∞。

首先考虑共轴对转系统的上旋翼,动量理论可以较好地解释通过旋翼环状面积的质量流量和诱导速度导致的推力增加。通过旋翼环状面积的质量流量速度表示为[13]

(2)

式中,dA=2πydy,那么环状面积上增加的推力为

dTu=2ρ(V∞+vu)vudA=4πρ(V∞+vu)vuydy

(3)

将推力转化为编撰的无量纲形式,上述方程可写为

(4)

式中,λ=v/ΩR,λu=vu/ΩR,λ∞=V∞/ΩR,r=y/R代表无量纲的径向位置。因此环状面积的拉力系数可以写为

dCTu=4λλurdr=4λ(λ-λ∞)rdr

(5)

BEMT中的桨尖损失可以通过普朗特桨尖损失方程进行计算,桨尖损失修正因子F的表达式如下

F=(2/π)cos-1(exp(-f))

(6)

式中,f通过叶片数目Nb和叶片单元的径向位置r给出,表达式如下

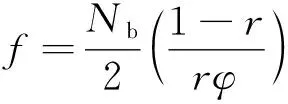
(7)

式中,φ=λ(r)/r是小角度假设下的入流角。那么普朗特桨尖损失方程修正的环状面积拉力系数表示为

dCT=4Fλλurdr

(8)

运用经典叶素理论,桨盘上相同环状面积的所产生的拉力表示为

(9)

式中:θu是指上旋翼的叶片扭转角,可能包含了叶片截面的零升力迎角;σu为桨盘实度。将经典叶素理论与叶素动量理论所获得的拉力系数进行联立求λ的方程,可得

(10)

式中,λu=λ-λ∞。上式在桨盘一系列离散单元上可以得到数值解。

同样的数学原理可以应用于下旋翼的分析。根据前面的假设,下旋翼一部分工作在上旋翼的滑流区域,在理想状态下,根据流管收缩可以求得颈缩面积Ac=πa2R2,其中a=0.707,Ac/A=0.5。可求得下旋翼上方的颈缩截面流速为V∞+vu/a2。

与上旋翼的计算方法类似,受上旋翼滑流影响区域(r≤a)的下旋翼流速可求得

(11)

式中:θl是指下旋翼的叶片扭转角,λl=λ-λ∞。

对于没有受到上旋翼滑流影响的区域(r>a),流速计算如下

(12)

方程(10)～(12)给出了上下旋翼各个离散径向位置在任何叶片桨距、叶片扭转以及翼型截面情况下的流速近似计算方法。

根据上述拉力系数计算公式以及流速计算公式,旋翼的拉力、功率和扭矩就可以对每个桨盘进行数值积分来获得。上旋翼、下旋翼和总拉力系数表达式如下

本文在上文中BEMT理论建立的共轴双旋翼气动力模型基础上，提出了基于CFD数据与实验数据的共轴双旋翼涵道升力风扇空气动力学模型。涵道和唇口的存在,一定程度上影响了上旋翼的诱导速度,而对下旋翼的气动力几乎没有影响,因此对上旋翼的诱导速度λ通过CFD数据和实验数据进行了修正,修正系数为η。气动部件的气动力是通过BEMT进行积分计算得到的,在数值计算方面有较好的应用,但是对于升力风扇气动力的解析式是相当复杂的,因此文中提出了运用特征截面的气动数据来表达整体气动数据的方法。同样根据CFD数据和实验数据进行了数据修正,以螺旋桨r/R=0.6处的截面参数为升力风扇计算的特征截面参数。

图4 升力风扇

升力风扇在飞行器运动过程中其远场速度与飞行器的飞行参数密切相关,具体可表达为

V∞=-Vz+qLfanG

式中：Vz为飞行器z向速度；q为俯仰角速率；LfanG为升力风扇中心到飞行器重心的水平距离。由公式(10)结合实验数据加以修正得出上旋翼的无量纲诱导速度

(16)

其中特定涵道唇口的修正系数为η=f(V∞)。特征截面处的上旋翼拉力系数为

(17)

对于下旋翼无桨尖修正的无量纲诱导速度,由于涵道壁的影响,下旋翼基本不存在颈缩现象,即公式(11)颈缩系数a=1,由此计算下旋翼无量纲诱导速度

(18)

特征截面处的下旋翼拉力系数为

(19)

2.2 推力涵道气动力模型

与升力风扇类似,运用BEMT理论,建立推力涵道的气动力模型,其中推力涵道属于多叶片高转速涵道,其叶片弦长从根部到尖部基本保持不变,其叶片桨尖损失较小,这一点与升力风扇建模有所区别。并且,涵道存在转子叶片和定子叶片,即下叶片不转动,模型的等效拉力由上旋翼转子产生,同样运用CFD数据和实验数据进行模型修正,其计算方法如下。

图5 推力涵道

推力涵道上旋翼转子诱导速度计算为(20)式,式中计算方法是在公式(16)的基础上去掉了桨尖修正系数F得来,其推力涵道对应的远场速度可表示为V∞=-(Vz+qLductG)sinθd+Vxcosθd。

(20)

特征截面处的上旋翼拉力系数计算为

城市旅游效率时空格局会受到资源、经济市场结构以及政策等各种因素的影响，这些因素会推动空间格局不断变化、演化。不同区域的作用机制就是时空格局发展的内在驱动力。根据研究以及理论分析，综合分析变量的代表性以及数据的可获取性，其主要的影响因素主要有旅游资源禀赋(RES)、旅游接待设施规模(TF)、城市基础设施条件(PTlJ)、产业结构(STR)、外贸依存度(TRA)、政府规模(GOV)等几点因素。

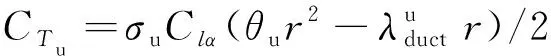
(21)

3 飞行动力学建模

对于存在涵道偏转的刚性无人机,六自由度方程可以较好地描述其飞行运动,其动力学模型满足方程(22)～(23)。合外力F由飞行器各部件的空气动力和重力组成,用Fx,Fy,Fz表示空气动力在机体轴系下的三分量,∑M为外力对机体坐标系原点的力矩之和。将机体轴系下的全量方程在基础运动的条件下进行线化处理,可以得到飞行器线化运动方程[14]

(22)

(23)

(22)～(23)式中等号右边为扰动引起的空气动力和力矩的变化,除了前面提到的运动参数扰动外,操纵人员的操纵也是引起无人机空气动力和力矩变化的扰动因素,但文中重点研究无人机的自身稳定性,认为飞行器在研究范围内无操纵稳定飞行,那么空气动力和力矩的小扰动表达式为

式中,∂Fx/∂u,…,∂Fx/∂r为气动导数,其值按照基准飞行状态的飞行参数来确定,与扰动运动中的参数变化无关,同样∑ΔFx,…,∑ΔMz的小扰动表达式与之类似。

根据机体轴系形成过程可以求得机体旋转角速度在机体轴系上的投影,进而可以求解出姿态角与角速度之间的运动学关系方程,最终按小扰动条件进行线化处理,可以得到飞行器的小扰动线化运动学方程组[15]

(24)

(25)

(26)

4 案例无人机纵向稳定性分析

4.1 平衡方程及求解

4.1.1 悬停平衡

垂直起降无人机在悬停阶段,作用在其上的力和力矩如图6所示。在悬停过程中,只有升力风扇和增升涵道作为动力,机翼不提供气动力,在机体轴系下建立无人机力和力矩纵向平衡方程。

图6 无人机悬停受力分析

(27)

式中：m为全机质量；l为作用力臂长度；θ为俯仰姿态角。

在一定俯仰姿态角θ下求解方程组(27)可得在悬停平衡状态下的升力风扇推力Tfan,推力涵道推力Tduct和推力涵道偏转角θduct。

图7 悬停配平结果

4.1.2 过渡平衡

在过渡平衡状态下,力学方程较悬停平衡状态多了自由来流在机体上产生的气动力和力矩,悬停受力示意如图8所示。

图8 无人机过渡受力分析

(28)

式中：L为升力；D为阻力；M为力矩。

方程组(28)在一定过渡姿态俯仰角下,求得不同速度下的过渡平衡的升力风扇推力Tfan,推力涵道推力Tduct和推力涵道偏转角θduct,如图9所示。

图9 过渡配平结果

4.2 纵向稳定性

通过本文升力风扇计算模型和推力涵道计算模型,可以在不同转速下、不同来流速度的推力。模型计算与CFD计算和实验数据比较接近,误差在5%以内,将3种数据集中在图10中,能直观地看出数据吻合度,证明了文中建立模型的准确性。

图10 升力风扇数据对比

由悬停特征根分布图11可以看出,只有在俯仰姿态角为0°的时候,其纵向稳定性表现出2个零根和2个不同的负实根,其纵向稳定性表现为中立稳定模态和单调收敛模态;当无人机悬停姿态角小于零时,其存在一对实部为正的共轭复根,振荡发散,同时存在一正实根和一负实根,致使系统处于发散状态;同样当悬停俯仰角大于零的时候,存在一对实部为负的共轭复根和2个正实根,存在振荡收敛长周期模态和单调发散运动。在整个悬停姿态角范围内,根据四次特征方程的Routh-Huewitz稳定性准则判定,其在悬停过程中纵向表现为不稳定。

图11 悬停根轨迹变化 图12 速度1～4 m/s纵向根轨迹图13 速度5～20 m/s纵向根轨迹

过渡过程中总的气动力比悬停过程中多了机身气动部件产生的气动力,其气动导数可以通过CFD计算软件求得,在固定姿态角的过渡过程中,随着过渡速度的增大其纵向特征根变化如图12～13所示。图12为过渡速度从1～4 m/s时的纵向特征根变化趋势,根据特征根表现和劳斯判据可知在这个过渡速度期间,其纵向稳定性为不稳定状态。当速度大于5 m/s时,其特征根表现为图13,其特征根表现为2个实部为负的复根和2个负实根,表现为长周期模态和过阻尼模态特征,根据Routh-Huewitz判据可以知道在此过渡速度下其纵向稳定性为稳定状态。

在悬停状态下,根据飞行器吊挂试验,在悬停状态下,无控制参与的情况下,保持飞行器悬停,并给予初始纵向扰动,通过飞行控制器记录反馈数据,如图14所示,可以验证俯仰扰动下的振荡模态与本节悬停稳定性计算结果吻合。根据本节悬停特征根可计算得悬停状态下其纵向振荡收敛模态特征周期为100～101量级,在吊挂实验飞行控制器采集数据端能够较好地观测其振荡周期数据如图15所示。在俯仰扰动中俯仰姿态角曲线振荡周期可以计算得出,其收敛平均振荡周期为7 s,与文中纵向稳定性计算结果中的振荡模态特征结果基本保持一致,从而验证文中稳定性计算方法在表述此飞行器纵向运动时的准确性。

图14 悬停吊挂实验 图15 悬停吊挂实验曲线

5 结 论

本文通过叶素动量理论、实验数据参数辨识方法、带质量偏转的六自由度方程和模态特征分析方法对涵道式垂直起降固定翼无人机进行了研究,可以得出以下结论:

1) 文中基于BEMT理论改善了带唇口的共轴双旋翼涵道的气动力模型和推力涵道模型,基于特征截面计算的模型,解析式修正参数根据实验数据辨识而来,此模型能够较准确地描述升力风扇的动力,误差在5%以内。

2) 以刚体六自由度方程为基础建立了带涵道质量偏转的飞行动力学模型,推力涵道质量偏转直接影响无人机的惯量,此模型能够较完整地描述此类无人机纵向运动状态。

3) 运用文中建模方法,基于模态特征,对案例无人机进行了纵向稳定性分析。在悬停状态下,只有0°俯仰姿态角时,无人机存在中立稳定和单调收敛模态,其他姿态角悬停纵向扰动运动均为不稳定状态。在过渡飞行时,在一定俯仰角下过渡,初始小速度1～4 m/s阶段,由其纵向根轨迹和劳斯判据可知其为不稳定状态;当速度大于5 m/s时,根轨迹表现为长周期模态和过阻尼模态,根据劳斯判据可知,在此状态下无人机纵向扰动运动是稳定的。

文中围绕此类涵道式固定翼无人机纵向稳定性进行了研究,下一步将在横航向稳定性和全机操纵性方面展开研究。