精心设计学习过程,促进深度学习的发生
武维民 张秋爽
【摘 要】深度学习,就是在教师的引领下,学生围绕着具有挑战性的学习主题,全身心积极参与、体验成功、获得发展的有意义的学习过程。因此数学学习要让学生经历缓慢的知识内化过程,让过程蕴含结果,让结果顺其自然生成。
【关键词】挑战性 问题链 深度学习 必备品格 关键能力
“好吃又有营养”的儿童数学教育是吴正宪老师鲜明的数学教育主张,多年来吴正宪老师带领其团队一直致力于儿童数学教育的研究。吴老师指出,儿童数学教育要关注两个重要的维度,一是关注儿童视角,要把握儿童的认知特点和学习规律,关注儿童的需求;二是把握数学本质,研究数学规律,让儿童拥有数学视角与数学思维。在坚守儿童立场和把握数学本质的同时使儿童数学从浅表学习走向深度学习,培养他们的迁移和创新能力,促进儿童的核心素养的发展。
一、勇于创设富有挑战性的学习过程,开启儿童的深度学习
如何更有利于儿童的学习?学生重复练习和教师反复讲解是学生最好的学习方式吗?小马过河的故事告诉我们,只有自己勇于去尝试,才能知道自己面临的问题是什么、解决问题的路径是什么。自主体验是最好的学习方法之一,学习应该是一个自主探索的过程,虽然在这样的过程中会遇到困难,有时甚至不知从何下手,但这正是学习的起点。突破一个又一个困难,体验一个又一个成功,积累一个又一个经验,正是学生解决新问题、提升思维能力的关键。
例如,在教学“平行四边形面积”的时候,教师一般第一步会复习长方形面积的计算方法;第二步出示标有数据的平行四边形,让学生猜测平行四边形的面积怎么计算;第三步提供方格纸让学生进行验证;第四步总结方法进行练习。整个学习的过程也体现了猜想、验证、归纳、总结的过程。
但仔细回想,这样的学习从一开始教师就按照自己的教学逻辑设计展开,是在已知的基础上寻找未知,是以获得结论为目的的。学生顺着教师精心搭设的脚手架,一步步开始了“顺利”的学习之旅。这种学习缺少了独立思考和挑战,也就少了思考的力量,学生头脑中也就不会主动把知识和能力建立关联。
史宁中教授曾说:“在小学阶段,我们至少要有一次让学生自己得出结论的过程。”吴正宪老师在教学“平行四边形的面积”时,一上课就在黑板上出示了一大一小两个平行四边形,问:“平行四边形的大小怎么求呢?每个小组都有一个平行四边形纸片,每个小组的纸片形状各异。老师这还有很多工具,你需要什么可以来取;做的过程中,有什么新想法,就可以找我这个大朋友商量。”学生面对真实的问题,稍做思考后纷纷来拿工具,有的要剪刀,有的要大长方形,有的要方格纸,还有的要胶带……
在日常教学中,大都是教师提前给学生准备学具,他们按照教师预设的轨迹进行学习;而吴老师的课堂,让学生自己设计方案、选择需要的学具,支持他们的个性化思考,同时也为展示多样化的解决问题策略提供可能。
挑战需要勇气,可能成功,也可能失败。面对困难不气馁,反思失败的原因,重新审视思考问题的角度……这些远远超出了一个正确结论本身。我们要给学生掉进陷阱又能自己爬出来的机会。挑战需要思考,要在已有的经验中寻找解决新问题的方法,在这样的过程中建立新旧知识和经验的关联,这正是学生自主将知识结构化的过程,也是他们学会学习的过程。在一个个的挑战学习中学生的创新意识、实践能力得以培养和发展。
二、精心设计问题链的展开过程,推进儿童的深度学习
问题是培养学生理性思考的重要手段,是数学学习的重要功能之一。在教学中,教师在学习目标的指导下,制定适切的核心问题,然后根据学生的学习进程,将其分解成子问题,形成问题链,把学习转化成解决问题的过程,提升学生解决问题的能力。
例如,吴正宪老师在教学“小数除法”时,出示了这样的“情境”:4个大学生共进晚餐,约定以“AA制”方式付费。一共花了97元。每人应付多少元?
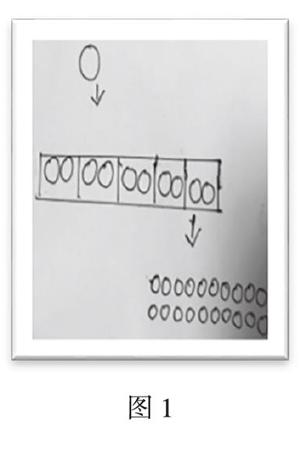
学生借助已有经验进行解答,结果困难出来了:余下的1怎么办呢?学生的自主探索出现了困难,而核心问题也随之出现了,他们自主解决的问题就呼之欲出了。吴老师就顺势给足了学生自主学习的时间和空间,于是出现了各种解决问题的方法。其中一些同学是这样解决的(如图1),吴老师引导学生把这样的方法与竖式的写法相结合,最后解决了问题。在解决的过程中,把核心问题分解成了以下问题:(1)1元分给4个人,每人多少元呢?(2)与竖式计算怎么结合呢?(3)计算结果是2425还是24.25呢?(4)如果没有元、角、分的帮助怎么思考呢?
在这样的问题展开中,学生渐渐理解小数除法的本质和整数除法是一样的,也是细分单位,只是余下个位的1转化了10个 1 /10,余下的十分位的2转化为了20个1 /100。核心问题引发深度的思考,深度学习也就发生了。这样的学习不只是学习一节课,更是学习一类课,小数除法勾连整个除法,也勾连整个运算。
通过对吴正宪老师课堂教学的分析,我们发现深度学习不仅强调学习者对知识和技能的深度理解,还强调在深度理解的基础上,将知识和技能迁移应用到实际问题的解决中,促进学生的深度思考和思维的结构化。
三、注重勾连知识的结构化过程,完善儿童的深度学习
深度学习打通了从“知识”到“素养”的通道,是瞄准学生核心素养、聚焦学科本质、关注学科关键问题、重视单元主题实施的学习。在以课时为单位的教学中,我们一般以知识学习为目的,学习到的是零散的、孤立的知识。以单元为基本单位进行学习,是用少量主题实现对知识的深度覆盖,立足学生素养的达成,关注学生迁移和创新能力的培养,这就是深度学习的特点。
吴正宪老师的课堂教学正是体现了深度学习的特点。我们再来看吴正宪老师在教学“归一问题”时的教学场景。
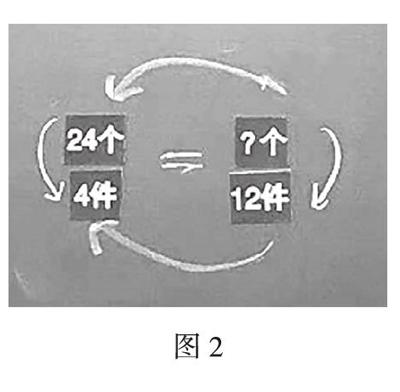
吴老师上课后出示问题情境:艺术节要到了,学校舞蹈队的孩子们需要表演,老师们决定在孩子们的衣服上钉上漂亮的珠子。4件衣服钉了24个珠子,12件衣服需要多少个珠子?在学生自主解决、全班同学进行交流、问题得到解决后,吴老师在黑板上摆放了四张数字卡片(如图2),然后请学生回顾解决问题的过程,并让学生思考这四个数之间的关系。学生很快发现24个和4件与“?”个和12件的关系是相等的。吴老师追问能否换个角度再找找还有没有其他的关系。在吴老师的追问下,个别学生发现12和4有3倍的关系,所以“?”和24也应该是3倍的关系。通过这样的观察,学生发现不仅竖着看有关系,横着看也有关系。不同的观察角度发现不同的关系,而解决问题就是要研究數量和数量之间的关系,“回顾与反思”不仅仅是对数据的检查,更重要的是对数量关系的再回顾,在此基础上,学生的思维在教师的引导下不断地扩展。
吴老师并没有止步于此。这节课吴老师带领学生解决了三个问题,12件衣服需要多少个珠子?买8个碗需要多少元?6小时行多少米?吴老师在引导学生整体回顾时,让学生感受到虽然解决的问题不同,但都是“老一”和“老多”的关系,在引领学生找到这一组题相同的结构后,吴老师继续引导学生用今天学习的“一”和“多”与以前学习的每份数、总数和份数建立联系,使新旧知识建立联系,打通一类知识。相信当学生遇到知多求一的问题时,会立刻启动头脑中的关联,解决新问题。同时吴老师又把速度、时间、路程,单价、数量、总价和今天学习的内容建立联系。通过一节课的学习,使学生感受到在“份”的基础上生长出的一串知识,这正是吴老师的结构化把握引发学生的结构化学习的结果。
吴老师的课堂总是让学生掌握学科的核心知识,理解学习的过程,把握学科的本质及思想方法,形成积极的情感体验。这样的学习不是在重复的训练中掌握知识,而是把学习内容作为素材,让学生在自主探索中将知识进行结构化,使学生具有解决一类问题的能力,培养学生的迁移创新能力。

