基于改进BESO方法的多工况船体开孔孔形优化
刘 昆,郭德松,王仁华,张延昌
(江苏科技大学 a.船舶与海洋工程学院;b.土木工程与建筑学院,江苏 镇江 212003)
0 引 言
在船体结构设计和建造过程中需要开设人孔、减轻孔、工艺孔等,开孔的存在会导致孔边应力增加,甚至产生应力集中。此外,随着结构轻量化要求的提高及船舶大型化发展趋势,传统开孔设计已无法完全满足当今船体结构的设计要求。同时,船舶典型设计工况较多,需考虑船体结构开孔在多工况下的综合优化设计,提高船体结构材料利用率,有效降低船舶结构重量。
拓扑优化设计是结构优化的一种,根据给定的负载情况、约束条件和性能指标,在给定的区域内对材料分布进行优化,从而设计出经济、安全的结构模型。双向渐进结构优化(Bidirectional Evolutionary Structural Optimization,BESO)算法已经成为非常成熟的连续体拓扑优化方法,其算法通用性好、优化效率高,可应用于船体开孔拓扑优化。
在BESO算法理论研究方面成果显著。XIE等[1]提出渐进结构优化(Evolutionary Structural Optimization,ESO)方法,QUERIN等[2-4]和YOUNG等[5]提出BESO方法,该方法解决了ESO方法只能单向删除单元的缺点,还可在高应力区增加单元。荣见华等[6]提出一种基于应力及其灵敏度的BESO方法,解决了优化过程中的震荡状态。
拓扑优化已被广泛应用于船舶结构设计领域。刘宏亮等[7]将单元生长进化算法结合变密度(Solid Isotropic Microstructures/Material with Penalization,SIMP)材料理论模型和有限元方程对大型油船(Very Large Crude Carrier,VLCC)中剖面横撑结构进行优化设计,得到一种VLCC轻量化的设计方案。王兴[8]提出一种改进的适用于开孔板的BESO算法,在ANSYS有限元软件中基于APDL语言编写优化程序,并对不同孔形的开孔薄板进行优化计算,结果显示拓扑优化可进行孔形优化计算。邱伟强等[9]对单纵舱壁型VLCC进行拓扑优化,建立油船舱段拓扑优化基结构,分别根据SIMP法和BESO法,以船体结构质量最轻为优化目标,结合CSR-H规范载荷条件和边界条件,得到油船舱段主要支撑结构下拓扑优化的清晰构型。尽管结构拓扑优化技术在船舶设计领域的应用已逐渐引起关注,但在船体板材开孔的拓扑优化方面还鲜有研究,因此,借助拓扑优化方法对船体板进行开孔优化。以船体梁腹板开孔为研究对象,引进含满意度权重因子的折中规划法,对传统BESO方法进行改进,提出一种适用于多工况船体结构孔形优化的BESO方法。
1 传统BESO方法
BESO方法是QUERIN借鉴满应力思想将ESO与AESO(Additive Evolutionary Structural Optimization)两种优化方法的优点相结合得到的,不仅能删除低效和无效的单元,而且能在高应力区增加单元,从而寻求结构最优解[4]。BESO方法解决了ESO方法只能单向删除单元的缺点,可在较少的优化区域内快速地优化出最佳构型。
基于应力的BESO方法的实现原理是在低应力区有层次地删除低应力单元,对于高应力区可在其周围添加单元以降低单元应力。通过引入单元添加率RI、单元删除率RR、稳态数NSS和振荡数NON确定每次迭代计算时单元的删除或添加情况[10]。
BESO方法优化得到的材料结构可更均匀地承担载荷,使材料结构中所有的单元应力更均衡。最大von Mises应力(第四强度理论)是常用的优化准则之一。
二维平面结构的von Mises应力为
(1)
三维立体结构的von Mises应力为
(2)
式中:σx、σy、σz分别为x、y、z方向的正应力;τxy、τyz、τzx分别为不同方向的剪应力。
对结构单元应力σe,vm和整体结构最大应力σmax,vm进行商运算:若两者比值小于当前的单元删除率RR,则表明这类单元属于低应力单元,需要进行删除;若其比值大于当前的单元添加率RI,则表明这类单元属于高应力单元,其周围需要添加单元;若其比值处于RR与RI之间,则这类单元需要保留[10-11]。
2 改进BESO方法
传统的BESO方法在全局范围内寻求最优布局,无法只对开孔进行优化,需要进行改进以应用于船体结构孔形优化设计。将体积减轻比作为优化目标、孔边应力作为约束,基于含满意度权重因子的折中规划法,对传统的BESO方法进行一定的改进,以实现多工况船体开孔的孔形优化。
2.1 含满意度因子的折中规划法
2.1.1 折中规划法
解决多目标优化问题较常用的方法是线性加权法,这种方法在实际操作中较易实现,但在求解非凸优化问题时无法得到所有最精确的解。在构建多目标函数的方法中,折中规划法应用范围较广,可将多目标优化问题转换为单个数值的目标函数,然后把多目标优化问题的解转化为与每个目标函数的理想解距离最小的矢量,即把多目标优化问题转化为单目标优化问题[12]。
基于应力优化准则对折中规划法进行改进,基本原理为将多个工况的子目标函数转换为单目标函数,对每个工况下的单元应力进行归一化处理,使单元应力在0~1变化,然后对各工况下的单元应力进行合并,得到所有工况耦合后的单元应力。此方法可使优化后的结构明显减轻载荷的“病态”现象[13]。改进的数学模型为
(3)

2.1.2 满意度理论
折中规划法的不足在于设计者需要根据经验确定各目标所占比例的权重因子,此权重因子为静态值,不能精确地表示优化迭代的动态过程。将满意度理论与折中规划法相结合以控制权重因子wi,应用到BESO优化算法中使权重因子根据满意度的变化进行动态调整。
定义满意度因子q来衡量对优化过程的满意程度。q=1表示优化结果满意度最高;q=0表示优化结果满意度最低;当q为0~1的实数时,表示优化结果的满意度处于两者之间。满意度因子qk为
(4)
式中:Ck为目标函数值;Ck,n为第k个优化目标的最差值;Ck,m为第k个优化目标的最理想值。
满意度权重因子wk的表达式为
(5)
控制满意度权重因子能够改善权重对优化迭代过程的影响,从而使各优化目标达到相对平衡。
同理,基于应力优化准则,将孔边单元约束应力设置为式(4)中的最理想值,第k个工况下孔边单元最小应力设置为最差值,第k个工况下的单元应力设置为优化迭代值,则改进后的满意度因子为
(6)
式中:F为第k个工况下单元应力;FE,min为第k个工况下最小孔边应力;FY为第k个工况下孔边约束应力。
BESO方法不仅可删除单元,而且在应力大的单元周围需要添加单元,因此为更好地判断单元应力大小,改进后的满意度权重因子wk与满意度qk呈正相关关系。当迭代应力接近约束应力时,满意度qk相应增大,表明此单元应力大,可能属于高应力,需要在单元周围添加单元,单元满意度权重因子wk则相应增大;反之,当迭代应力接近孔边最小应力时,满意度qk相应减小,表明此单元应力小,可能属于低应力,需要删除单元,单元满意度权重因子wk则相应减小。改进后的wk为
(7)
2.2 传统BESO方法的改进措施
(1)将体积减轻比作为优化目标,孔边应力作为约束。体积减轻比V公式为
(8)
式中:Vf为每次优化迭代结束时的设计域体积;Vi为初始设计域体积。
(2)改进单元删除和添加的公式,两者为删除添加单元的判据。
(9)
式中:Fi为由式(3)得到的应力;Ft为应力阀值,其取值由实际优化要求决定。单元删除率RR和单元添加率RI计算式为
他目前最憧憬的事,就是到了50岁,还能有充足的热血开着越野吉普上路,彼时儿子19岁,可以拿到驾照陪他走这兄弟般的长途了,他将带着他,到那些镜头里的故事的发生地去,追溯父辈的青春。
RR=r0+r1NSS+aRRNON
(10)
RI=i0-i1NSS+aRINON
(11)
式中:r0、r1、i0、i1为常数,根据实际优化要求决定取值;aRR和aRI为振荡常数,同样根据实际的优化要求决定取值;NSS为稳态数;NON为振荡数。
2.3 改进BESO方法的实现步骤
根据第2.2节,首先设置模型结构参数特别是设计域的网格尺寸,对模型结构进行计算分析,然后根据含有满意度因子的折中规划法,得到优化过程中的动态权重系数及式(3)中的应力,最后对孔边单元进行分析,判断单元是否删除或者添加。改进后的BESO方法的流程图如图1所示。

图1 改进BESO优化算法的流程图
3 算例验证与分析
通过ANSYS二次开发语言APDL进行编程,选取某船体梁腹板开孔结构,运用子模型技术得到优化域,通过改进BESO方法对开孔进行孔形优化,以检验改进后BESO方法的可靠性。
3.1 分析对象及有限元模型
如图2所示,船体梁结构梁长为4 680 mm,腹板高为380 mm,上翼缘宽为780 mm,下翼缘宽为160 mm。腹板的椭圆开孔长为760 mm,宽为190 mm,两端圆弧直径为190 mm。结构的有限元模型如图3所示,模型网格尺寸如下:非开孔区为80 mm,过渡区为40 mm,开孔区为10 mm,板厚为20 mm。材料为船用高强度钢,密度为7 850 kg/m3,弹性模量为206 GPa,泊松比为0.3。

单位:mm图2 开孔梁几何模型

图3 开孔梁有限元模型
3.2 约束载荷
船体梁结构的约束以及载荷如下:梁两端为固定约束,载荷工况1为均布面载荷1 N/mm2作用于开孔梁的上翼缘面板,工况2为均布面载荷1 N/mm2作用于开孔梁的下翼缘面板。
3.3 子模型方法
子模型方法又称切割边界位移法或特定边界位移法。切割边界就是将子模型从整个较粗糙模型分割开的边界。整体模型切割边界的计算位移即为子模型的边界条件。子模型基于圣维南原理,即如果实际分布载荷被等效载荷代替后,应力和应变只在载荷施加位置附近有改变。这说明只有在载荷集中位置才有应力集中效应,若子模型的位置远离应力集中位置,则在子模型内就可得到较精确的结果[14]。
在此船体梁结构中,开孔区域上下边界存在面板,左右边界有肘板,因此只需考虑腹板开孔周围区域。通过子模型技术,将船体梁结构进行切割,得到所需的子模型。图4为工况1下局部放大模型开孔附近区域的应力分布与子模型技术分析得到的开孔附近区域的应力分布,将两者进行对比,子模型中应力分布与局部放大模型的应力状态完全吻合。因此,开孔子模型技术可代替整体模型分析,准确地模拟孔边应力分布情况。
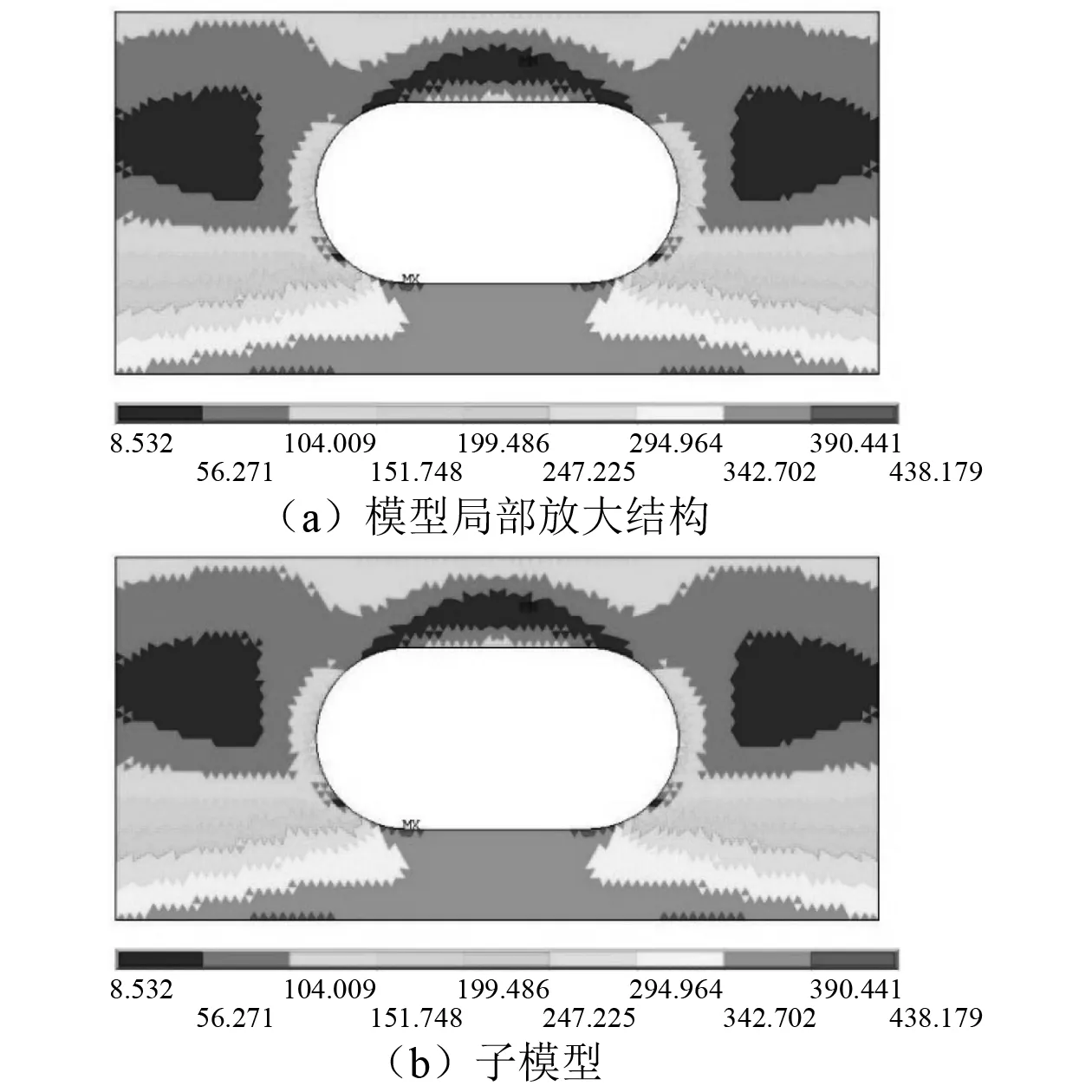
图4 局部放大结构与子模型对比(工况1)
3.4 结果比较
3.4.1 优化过程及结果分析
图5为子模型结构的优化迭代进程。由图5可知,随着优化迭代的进行,开孔面积不断增大,孔形从腰圆孔变成了近似倒扣碗形,在37次优化迭代后,优化目标体积减轻比达30.01%,并且单元最大应力没有超过应力约束(550 MPa),说明开孔结构达到所设定的优化条件的最佳构型。同时在优化过程中没有出现棋盘格现象,这就表明改进的单元删除、添加公式可靠。

图5 优化过程中的拓扑变化
根据优化结果,对优化前后的结构孔形进行对比,由图6可知,优化后的孔形体积明显增大,在优化历程中腰圆底部边界单元不断被激活以弥补较弱的下翼缘,使得开孔下边界成为一条水平边界,而上部边界及两侧单元由于应力较低被逐渐删除,开孔形状由原来的腰圆形变成了近似倒扣碗形。
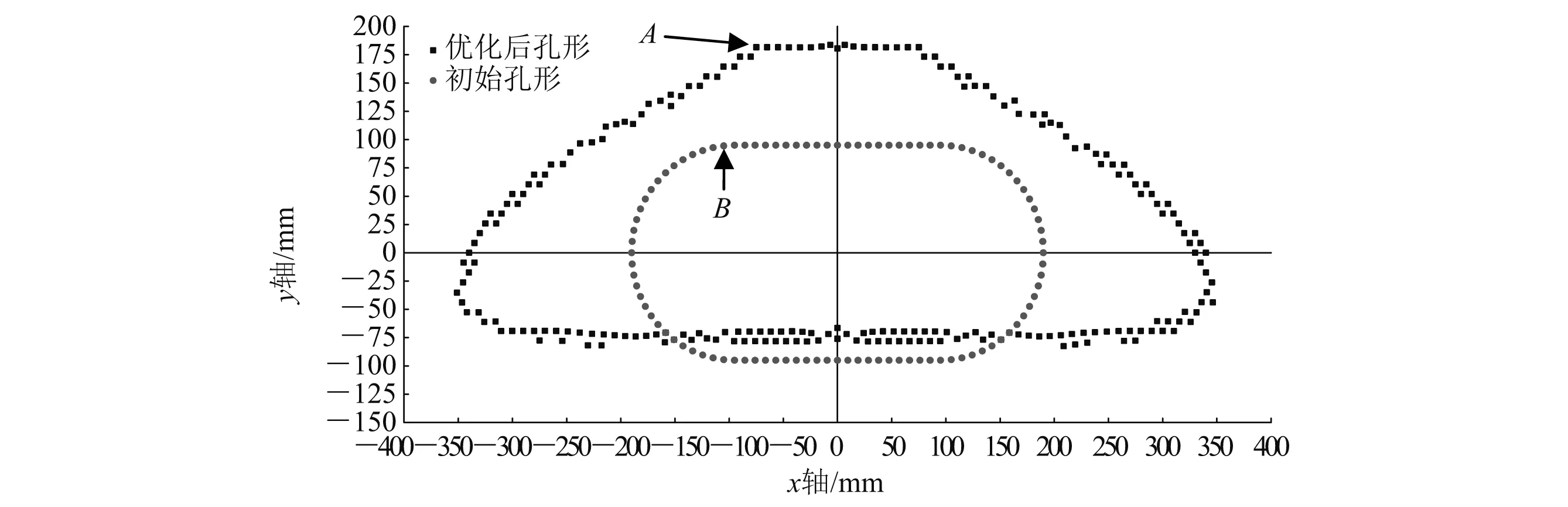
图6 优化前后孔形对比
图7为优化前后设计域单元应力云图:在孔形优化前,最大应力集中在开孔的下边界至设计域的下翼缘,这一区域的应力接近应力云图的最大值,表明开孔的存在导致应力集中现象产生;在孔形优化后,开孔的边界单元没有出现大片区域的应力接近应力云图的最大值,只有个别单元的应力接近最大值,说明优化后的孔形并不存在应力集中现象,而且单元应力分布更均匀、合理。

图7 优化前后设计域单元应力云图
表1为优化前后两工况孔边应力对比:在工况1载荷下,孔边最大应力由438.18 MPa降至407.73 MPa,最小应力由18.82 MPa升至34.01 MPa,孔边最大应力降低且最大与最小应力间的差值减小;在工况2载荷下,最大应力由90.01 MPa升至143.42 MPa,2个工况最大应力之间的差值缩小,使应力分布更均匀,最小应力的变化可忽略不计。
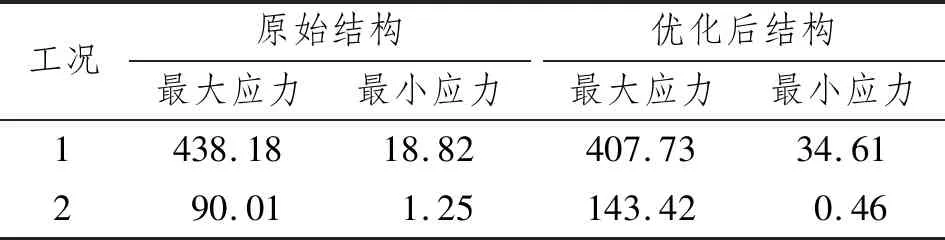
表1 优化前后两工况孔边单元应力对比 MPa
3.4.2 孔边应力及体积分析
图8为2个工况下孔边最大应力变化图与体积减轻比变化图。由图8可知,在优化过程中:工况1的孔边最大应力不断变化,呈现波动趋势,但是最终的孔边最大应力小于初始结构的最大应力,并且没有超出应力约束;工况2的孔边最大应力呈现上升的趋势,与初始相比更接近约束应力;体积减轻比随迭代次数的增加不断上升,表明优化减重效果明显。

图8 孔边最大应力与体积减轻比变化曲线
图9为优化前后2个工况的孔边应力变化对比图:优化后孔边单元应力曲线横轴为以图6中A点为起始点,顺时针绕孔边一周的单元所对应的角度;初始孔边单元应力曲线横轴为以图6中B点为起始点,顺时针绕孔边一周的单元所对应的角度。工况1,优化后孔边单元被删除,开孔边界不光顺,导致优化后的孔边应力波动较大,与优化前相比孔边应力变化趋势不明显,但是优化后的孔边大多数单元应力处于100~300 MPa,少数超出300 MPa,优化后的孔边最大应力变小,最小应力变大,说明在此工况下,优化后的孔边应力相互靠近,单元应力差值减小,应力集中现象得到了缓解。工况2,由于初始应力值小,最大应力仅为90 MPa,与应力约束值(550 MPa)差距较大,因此在优化过程中低应力区的单元被删除较多,优化后整体应力较初始应力有所提高,优化后孔边应力处于0~150 MPa,不存在应力集中现象,表明结构材料利用率提升。

图9 优化前后孔边应力对比
由此,在船体梁腹板结构减轻30.01%重量的情况下,改进后的BESO方法可有效地缓解孔边应力集中现象,提升船体结构材料利用率,并且提高结构性能,达到轻量化的目标。
4 结 论
在传统的BESO方法基础上提出一种适用于多工况船体开孔孔形优化的改进BESO方法。以船体梁腹板开孔结构为研究对象进行优化,得到新式孔形,达到了轻量化的目的,并得出如下结论:
(1)建立含有满意度因子的折中规划法的多工况结构数学模型,通过算例证明该模型可为多工况优化问题提供动态权重系数,将多工况单元应力进行耦合,有效解决多工况船体结构优化问题。
(2)船体梁腹板开孔经过拓扑优化得到的新式孔形,在结构体积减小的前提下,缓解应力集中现象,提高船体结构材料利用率,体现了改进的BESO方法在孔形优化方面的有效性。
(3)改进后的BESO方法,改进了单元删除率与添加率公式,以体积减轻比作为优化目标,将孔边应力作为约束,可以在结构体积减小的情况下提高力学性能,达到轻量化的目的。
(4)采用改进BESO优化方法可得到在设定条件下的船体梁结构腹板开孔的最佳孔形,为船舶建造设计工程实际提供理论和技术支撑。

