带时变高阶矩的已实现GAS 模型及其实证研究

吴鑫育,王海运

（安徽财经大学 金融学院，安徽 蚌埠 233030）

0 引言

波动率在衍生产品定价、资产配置以及风险管理等众多金融应用中发挥着重要的作用.因此，波动率建模和预测一直是金融计量经济学研究的焦点和热点.传统上，学者们最常使用GARCH 模型[1]和随机波动率模型[2]对资产收益率的动态性建模.由于波动率具有不可观测性，通常将波动率看作是时变参数引入到模型中，因此，GARCH 模型和随机波动率模型又被看作是时变参数模型.Creal 等[3]将时变参数模型分为观测驱动（obervation-driven）模型和参数驱动（pa‐rameter-driven）模型.参数驱动模型参数的时变性通过一阶自回归过程描述，参数估计时通常需要借助模拟方法进行计算，模型的估计较为复杂，随机波动率模型属于参数驱动模型.观测驱动模型参数的时变性基于过去的信息驱动，简化了似然估计，模型可以直接使用极大似然方法估计.因此，观测驱动模型在对波动率的动态性进行建模与应用时受到学者的青睐，GARCH 模型即属于观测驱动模型.

Creal 等[3]和Harvey[4]将观测驱动模型与时变参数的得分函数相结合，构建了广义自回归得分（gener‐alized autoregressive score，GAS）模 型.GAS 模 型 将 条 件密度函数得分作为时变参数的主要驱动，能够充分利用观测变量条件分布的信息，与此同时，具备其他观 测 驱 动 模 型 优 点.Creal 等[5]、Lucas 等[6]和Harvey[4]和Luati[7]验证了GAS 模型在金融市场中应用的有效性.后续一些学者对GAS 模型进行扩展并运用到金融实践中[8-10].

一些学者基于GAS 模型框架，构建了时变波动率模型，例如Creal 等[11]、Blasques[12]以及Nystrup[13].国内学者对GAS 波动率模型的相关研究还较为少见，例如姚萍等人[14]的研究.传统GAS 模型与GARCH 模型相同，利用日度收盘价数据对波动率模型进行建模，忽略了日内价格变动的信息，从而影响波动率估计的准确性.随着计算机技术与信息储存技术的发展，利用日内高频数据对波动率建模受到了学者们的广泛关注.例如Hansen 等[15]提出了已实现GARCH 模型，Koopman 和Scharth[16]提出已实现随机波动率模型，Hansen 和Huang[16]提出了已实现EGARCH（REGARCH）模型，但是这些模型都未能充分利用观测变量条件分布的信息.基于此，一些学者基于GAS 模型引入日内高频数据.Opschoor 等[18]将已实现测度引入HEAVY GAS 模型，提出了一个新的多元波动率模型；Hansen等[19]基于得分驱动框架构建了已实现Wishart-GARCH模型.在国内，王天一和黄卓[20]将GAS 模型框架引入厚尾已实现GARCH 模型，提出了已实现GAS-GARCH（RGAS-GARCH）模型，沈根祥和邹欣悦[21]提出了RGAS-HEAVY 模型；上述研究表明引入已实现测度的GAS 模型相对于传统已实现波动率模型具有更好的实证效果.

然而，上述研究还没有将高阶矩特征纳入波动率模型中，Amaya 等[22]、Do 等[23]和Shen[24]的研究表明，考虑高阶矩特征有助于提升资产收益率预测的精确性.最近，朱鹏飞[25]提出了集成EEMD-SJC Copula-GARCHSK 套期保值比率估计模型，研究表明引入高阶矩后的套期保值模型具有更好的参数估计效果.上述研究中高阶矩被当作常数纳入模型中，越来越多的研究表明高阶矩具有时变性.León[26]、王鹏[27]以及吕永健和王鹏[28]的研究表明考虑高阶矩的时变性能更好地测度金融市场风险.同时考虑已实现测度以及高阶矩时变性的研究较为少见，Wu[29]提出了REGARCH-SK 模型.上述研究表明，对于资产收益率序列表现出尖峰厚尾特征的金融市场，考虑时变高阶矩能够更有效地预测风险值.但是，这些研究未能充分利用观测变量条件分布的信息，且对极端值的预测不够稳健.

鉴于此，本文结合GAS 模型框架，对资产收益率以及已实现测度联合建模，假设金融资产收益率服从时变学生t分布，构建能够捕获时变高阶矩特征的TVPRGAS 波动率模型.模型同时引入已实现测度，能够更好地利用价格变动包含的日内信息.TVP-RGAS 波动率模型通过对时变参数得分函数的设定，能够充分利用观测变量条件分布信息，且对极端值的预测较为稳健.由于该模型属于观测驱动模型，可用极大似然方法直接估计参数，模型具有易于实现的优点.本文采用上证综合指数，对TVP-RGAS 波动率模型进行实证研究，与其他已实现波动率模型在条件方差预测以及VaR 预测上进行实证比较分析.

1 模型构建

TVP-RGAS 波动率模型对资产收益率rt和对数已实现测度xt联合建模：

其中，μ表示资产收益率的条件均值，σt表示资产收益率的条件波动率，zt表示与度量误差ut相互独立标准化的信息.Zhu 和Galbraith[30]、杨兴林和王鹏[31]研究发现学生t分布能够很好地捕获资产收益率序列的尖峰厚尾特征.因此，本文假设rt服从学生t分布.对于已实现测度，本文使用Hansen等[32]在已实现GARCH 中使用的方法，假定对数已实现测度xt服从正态分布，可以得到rt和xt的条件概率密度函数为：

已有大量研究表明，波动率以及高阶矩具有时变性[32,33].此 外，Gómez[34]以 及Lacus 等[35]验 证 了 学 生t分布的自由度υ（υ＞2）是时变的.因此，除了假设波动率是时变的，本文还假设自由度参数υt也是时变的.

为了刻画时变波动率以及时变自由度参数的动态性，本文采用Creal 等[3]提出的GAS 得分框架.具体地，令ft=(f1，t，f2，t)'，其中f1，t=λt，υt=2+exp(f2，t).在此设定下可以确保时变参数υt＞2，因此学生t分布的方差总是存在，时变参数ft基于GAS 模型框架下的动态性为：

其中，参数A表示时变参数对得分新息的反应，参数B表示时变参数的持续性，st是条件分布的得分，St是标度矩阵.本文使用Russell 和Engle[36]在得分驱动模型中设定标度矩阵的方法，假设St=I，I是一个单位矩阵.lt是rt和xt的对数联合条件概率密度函数，Ft-1是t-1 时刻可观测的信息集，θ是非时变参数向量.可以看到，GAS 框架对时变参数动态性的设定充分利用了条件分布的信息，保证了模型设定的合理性.

由此，可以得到时变参数f1，t以 及f2，t的动态过程为：

据此可以得到时变参数f1，t以 及f2，t的得分s1，t以及s2，t为：

其中，γ(υ)=lnΓ(υ).

方程（1）-（6）即构成TVP-RGAS 波动率模型.TVPRGAS 波动率模型对资产收益率和已实现测度联合建模，引入已实现测度充分利用资产收益率日内变动信息，同时可以捕获时变高阶矩信息，是一个较为灵活的模型.通过约束A2=B2=0，此时时变参数υ变为常数，TVP-RGAS 波动率模型退化成带常数高阶矩的RGAS 波动率模型，进一步令ω2=0 得到不包含高阶矩信息的RGAS 波动率模型.

由于TVP-RGAS 波动率模型属于观测驱动模型，具有易于实现的特点，可用极大似然方法直接估计参数.其对数似然函数的形式如下：

其中，Θ是模型的参数向量，通过最大化似然函数可得到TVP-RGAS 波动率模型参数的极大似然估计

2 实证分析

2.1 数 据

本文选取上证综合指数（SSE）从2005 年1 月4 日至2020 年9 月30 日共3642 个交易日的5 分钟高频交易价格数据和日收盘价数据进行实证分析.所有数据均来源于wind 资讯.

定义第t个交易日的指数收益率为rt=pt-pt-1，其中pt是第t交易日的指数对数收盘价格.本文选取已实现方差作为已实现测度，其优势是可以充分利用高频数据所包含的日内信息，使模型可以更好地拟合数据.然而，实际中由于受到非交易时间和微观结构噪声的影响，RV 往往是真实日度波动率的有偏估计，需要进行偏差修正.

表1 给出了上证综合指数的日度指数资产收益率rt以及对数已实现测度log(RVt)的描述性统计量.从表1的结果来看，上证综合指数的日度指数资产收益率rt的均值大于0，偏度小于0，峰度大于3，呈现出左偏以及尖峰厚尾特征.Jarque-Bera 统计量显著，拒绝其为正态性的假定.上证综合指数的对数已实现方差log(RVt)的偏度接近于0，峰度接近于3，Jarque-Bera统计值接近于正态分布.

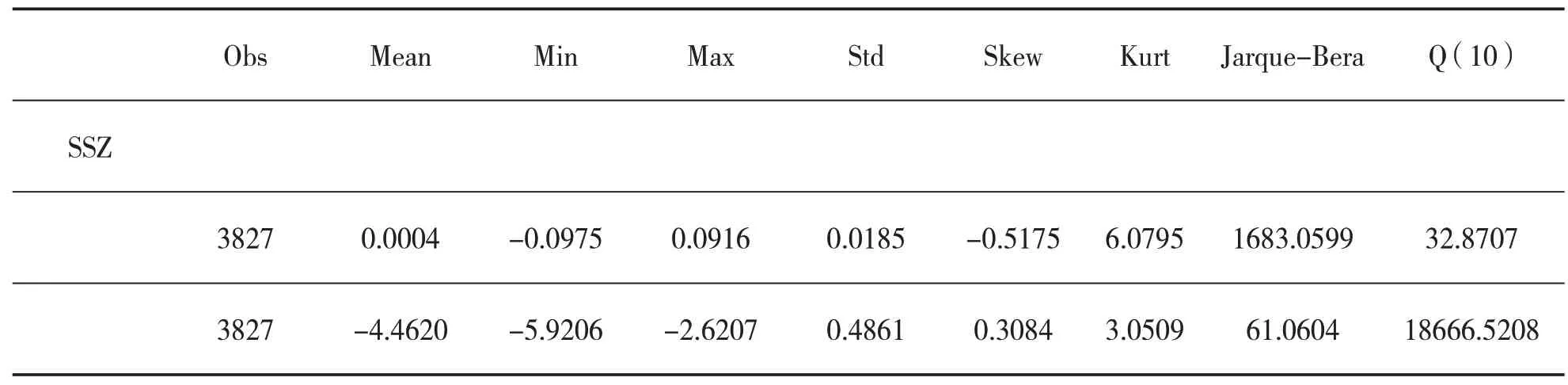
表1 指数日度资产收益率以及对数已实现测度描述性统计量

图1 给出了上证综合指数的日度指数资产收益率rt的QQ 图.从上证综合指数的日度指数资产收益率rt的QQ 图可以看出，上证综合指数的日度指数资产收益率rt不服从正态分布.这和Jarque-Bera 统计量得出的结论一致.

图1 上证综合指数的日度指数资产收益率rtQQ 图

2.2 参数估计结果

运用极大似然方法得到TVP-RGAS 波动率模型以及RGAS 波动率模型的参数估计结果以及标准误差、对数似然（Log-lik）和赤池信息准则（AIC）如表2所示.

由表2的结果可以看出，上证综合指数中RGAS 波动率模型与TVP-RGAS 波动率模型中的杠杆系数τ1和τ2十分显著，且τ1的估计值小于0，τ2的估计值大于0.说明国内股市存在明显的杠杆效应（波动率的非对称性）.上证综合指数中参数A1，A2的值接近于1，说明波动率和自由度参数的持续性较强.上证综合指数已实现方差的偏差调整系数ξ的估计值明显小于零，表明上证综合指数代表的股市已实现方差RV 是真实日度波动率的下偏估计，市场非交易时间效应强于微观结构噪声效应.从RGAS 估计出的υ的结果来看，上证综合指数具有明显的尖峰厚尾特征.因此，在对我国金融市场进行风险管理与控制时，需要充分考虑到收益率分布尖峰厚尾特征，从而更加有效度量市场风险.

表2 基于RGAS 波动率模型以及TVP-RGAS波动率模型参数的估计结果

比较RGAS 波动率模型的Log-lik 值和TVP-RGAS 波动率模型的AIC 值，可以判断模型对数据的拟合效果，其中对数似然值越大、赤池信息准则值越小说明模型对数据的拟合效果越好；TVP-RGAS 波动率模型相较于RGAS 波动率模型拥有更大的对数似然值以及更小AIC值，说明TVP-RGAS 波动率模型对数据的拟合效果要优于RGAS 波动率模型.

图2 给出了上证综合指数的收益率序列图、TVPRGAS 波动率模型对上证综合指数的已实现方差RV 样本内拟合图以及自由度参数υ序列图.由图2 可以看出，上证综合指数的收益率序列图呈现出尖峰厚尾特征，上证综合指数在抽样阶段内展现出明显的波动率时变性和波动率聚集性特征.TVP-RGAS 波动率模型对上证综合指数所代表的股票市场抽样区间内的已实现方差RV拟合效果较好.

图2 上证综合指数日度收益率rt 序列图、TVP-RGAS波动率模型对已实现方差RV的拟合图以及自由度参数υ 序列图

2.3 条件方差预测结果

为了考察TVP-RGAS 波动率模型的条件方差预测，本文采用RGARCH 模型、RGAS 波动率模型作为基准模型，比较TVP-RGAS 波动率模型和RGARCH 模型、RGAS波动率模型对条件方差预测精确性.为了能更好地比较TVP-RGAS 波动率模型以及RGARCH 模型对模型波动率预测精确性，选取均方根误差（RMSE）、平均绝对误差（MAE）以及均方误差（MSE）以三个损失函数作为评价指标：

其中，RV是观测的已实现方差，FV(m)是模型预测的波动率，m是波动率模型RGAS、TVP-RGAS 或RGARCH 模型.

表3 给出各模型波动率预测精确性评价结果，由表3可以看出相较于RGARCH 模型与RGAS 波动率模型，TVP-RGAS 波动率模型在三个损失函数评价指标下，均拥有最小的预测误差，因此TVP-RGAS 波动率模型对数据的条件方差预测要强于RGARCH 模型以及RGAS 模型.在多数情况下RGAS 波动率模型的预测效果要优于RGARCH 模型，说明结合GAS 模型框架能够在一定程度上提升模型对数据的预测效果.利用样本内数据估计模型，基于估计结果可以获得条件方差的预测值.在TVP-RGAS 波动率模型下，图3 给出上证综合指数基于TVP-RGAS 波动率模型得到的条件方差的预测结果.

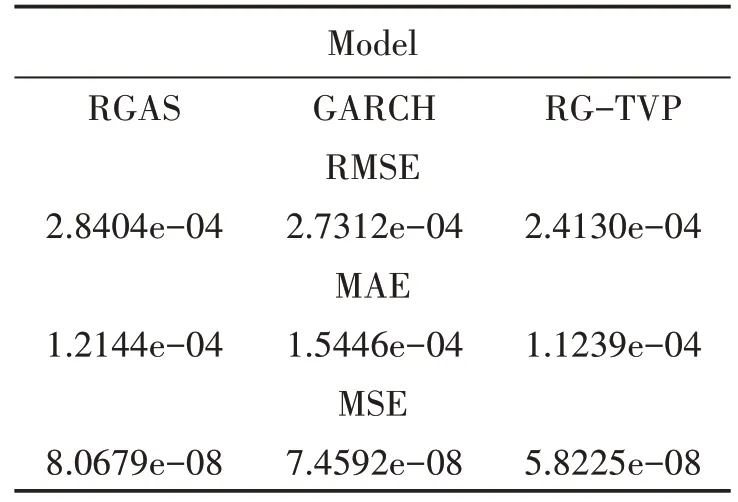
表3 上证综合指数的波动率预测结果

图3 上证综合指数指数条件方差预测结果

2.4 VaR 预测及后验分析

准确测量金融市场风险对于金融机构的生存和发展乃至整个金融系统的稳定至关重要.VaR 是市场风险管理中最广泛使用的工具，它因其概念简单、直观和易于计算等优点，成为许多风险管理者和金融机构计算市场风险的首选工具.下面基于TVP-RGAS 波动率模型的VaR 预测，讨论后验分析检验模型风险预测准确性.

VaR 是指在一定的置信度水平之下，某一金融资产或资产组合在未来特定时期的最大损失.t+1 时刻给定置信度水平1-α下的VaR定义为：

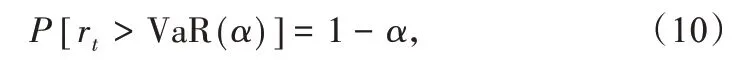
其中，P为概率，定义VaR 为负值，负号表示损失，rt≤VaR(α)定义为“失败事件”.由上式可得TVP-RGAS 波动率模型的VaR的计算公式为：

其中，zα是资产收益率新息分布的α左尾分位数.实际上在TVP-RGAS波动率模型的假定下，zα是标准化t分布的分位数.

为了检验VaR 预测的准确性，我们采用了文献中常用的后验分析方法，即失败率检验、Kupiec[37]引入的非条件覆盖的似然比检验和Christoffersen[38]引入的条件覆盖的似然比检验.非条件覆盖的似然比检验的具体形式为：

其中，T表示VaR 预测的总次数，T1表示“失败事件”发生的次数，记为“失败次数”，失败率π=T1/T.非条件覆盖的似然比检验LRuc不能保证“失败事件”不受到前一次“失败事件”的影响，因此Christoffersen[38]构建了独立检验.该检验假设“失败事件”发生与其上一次“失败事件”发生是独立的，假设成立时，似然函数比值LRind的形式为：

其中，π01=T01/(T00+T01)，π11=T11/(T10+T11)，π2=T01+T11/(T00+T01+T10+T11)，Tij表示两次事件的发生，若i，j=0表示本次测度成功，即rt＞VaR(α)，i，j=1则表示本次测度失败.Christoffersen[38]将非条件覆盖的似然比检验与独立检验相结合，建立了条件覆盖的似然比检验LRcc，其形式如下：

2.5 VaR预测及后验分析结果

利用样本内数据估计模型，基于估计结果可获得条件方差的预测值.利用（10）式以及条件方差的预测值，可以得到上证综合指数的VaR 结果.本文选取置信度水平为97.5%和95%（或显著性概率水平2.5%和5%），得到TVPRGAS波动率模型下VaR预测结果如图4所示.

图4 上证综合指数VaR 预测结果

表4 给出了RGARCH 模型、RGAS 波动率模型与TVP-RGAS 波动率模型下的后验分析结果，包括失败率（FR）以及非条件覆盖似然比统计量LRuc和条件覆盖测试的似然比统计量LRcc.从表4 可以看出，TVP-RGAS 波动率模型的预测效果要优于RGAS 以及RGARCH 模型的VaR 预测效果.TVP-RGAS 波动率模型在α=0.025 和α=0.05 时通过了显著性为5%的所有非条件覆盖（LRuc）和条件覆盖（LRcc）的似然比测试，而RGAS 波动率模型在α=0.025 时没能通过非条件覆盖（LRuc）和条件覆盖（LRcc）的似然比测试，RGARCH 模型在α=0.05 时没能通过非条件覆盖（LRuc）和条件覆盖（LRcc）的似然比测试.此外，TVP-RGAS 波动率模型总是拥有最接近显著性概率水平的FR 值.由此可以看出，与RGAS 波动率模型相比，引入了高阶矩特征的TVP-RGAS 波动率模型拥有更好的VaR 预测效果；与RGARCH 模型相比，可以描述厚尾分布的TVP-RGAS 波动率模型的VaR 预测更充分地利用了市场信息，更加合理地刻画了资产收益率的尾部分布及波动性，从而改进了VaR 预测精确性.

表4 上证综合指数的VaR 预测的后验分析

3 结语

本文基于传统的GAS 模型框架，引入包含日内信息的已实现测度，假设资产收益率服从能够捕获尖峰厚尾特征的学生t分布，构建能够捕获时变高阶矩信息的TVP-RGAS 波动率模型.采用上证综合指数的5 分钟高频数据进行实证研究，得到以下研究结论：

（1）上证综合指数日度指数收益率rt序列的偏度小于0，峰度大于3，呈现出左偏以及尖峰厚尾特征.同时Jarque-Bera 统计量显著，说明日度指数收益率rt序列不服从正态分布.

（2）沪市已实现波动率的偏差修正参数ξ的估计值明显小于0,表明已实现波动率是真实日度波动率的有偏估计,存在明显下偏，沪市非交易时间效应强于微观结构噪声效应.

（3）根据极大似然值以及AIC 对模型进行比较分析，TVP-RGAS 波动率模型比RGAS 波动率模型拥有更好的数据拟合效果.

（4）根据三个损失函数得到的各模型波动率预测精确性评价结果，相较于RGAS 波动率模型以及RGARCH模型，TVP-RGAS 波动率模型总是拥有最小的计算误差，即拥有更好的波动率预测效果.

（5）基于VaR的估计结果表明，相较于RGAS 波动率模型和RGARCH 模型，TVP-RGAS 波动率模型能够更好地测量金融市场风险.

本文的研究工作为时变高阶矩视角下对波动率建模提供了一种原理简单且效果较好的方法，同时丰富了市场风险测量的实证结果.值得注意的是，本文的工作还有待进一步的扩展与完善，例如将能够包含多种情况的偏斜广义t分布（SGT）引入到TVP-RGAS 波动率模型中，在多个市场进行实证分析.当然，将模型运用在资产组合管理与衍生产品定价等问题中，也是切实可行的研究方向.