辩证思维美学在高考数学试题中的渗透分析

广东省广州市源雅中学(510540)吴新华

广东省中山市桂山中学(528463)余铁青

高中数学教育教学的目的是培养提升学生的素养,提升学生通过数学学习,利用数学思维,数学知识认识世界和解决问题的能力.在高考这种具有极强选拔功能的考试中,在强调基础知识掌握的基础上,试题中明显将辩证唯物思想进行了有效渗透.高考数学真题中的辩证思维的渗透考查也是对学生能力考查的一个体现.

1 辩证思维的内涵与高考数学试题的关系

辩证思维是反映和符合客观事物辩证发展过程及其规律性的思维.对客观辩证法和认识过程辩证法的一定程度的认识和运用.辩证思维的特点是从对象的内在矛盾的运动变化中,从其各个方面的相互联系中进行考察,以便从整体上、本质上完整地认识对象.辩证思维运用逻辑范畴及其体系来把握具体真理.辩证思维既不同于那种将对象看做静止的、孤立的形而上学思维,也不同于那种把思维形式看作是既成的、确定的形式逻辑思维.它是辩证逻辑研究的对象.人类的辩证思维的历史发展经历了一个从自发到自觉的过程.

高考数学考的不仅仅是数学知识,考查的应该是更深层次的马克思主义的认识论问题.如果说数学知识本身的积累有助于学习者通过运用知识来解决实际问题,给决策提供有力支持.那么辩证思维的力量则是方向的把控问题,是思考问题方式的问题.从高度上看,数学高考试题的命制在考查知识的同时更应注重辩证思维的渗透,思维方式的引领,这实质是一种辩证的唯物主义美学潜移默化的影响.

2 高考真题辩证思维实例赏析

2.1 “变与不变”的辩证思维

评注辩证唯物主义认为,事物的运动发展是变与不变的统一.变与不变两者相互区别、相互对立.本来函数的自变量是x,后通过等价变形得到关于x的等价方程.虽然形式上发生了变化,但本质上还是在讨论曲线与直线的交点问题.通过有效的转变,把右边的直线进行了简化,变成了一条平行于x轴的直线,降低了解题难度.学生能够充分利用所学对勾函数进行绘制草图,极大的减少了直接求导计算到来的烦杂运算,本题的设计还有一个极具美学意义的处理之处就是g(x)的分段形式,整个图像两端都可以配方构造对勾函数,将这种图像的美学之感展现的淋漓尽致!

2.2 “整体与局部”的辩证思维

评注任何事物都有它的整体和局部.整体和局部二者既相互区别又相互联系,整体处于统率的决定地位;局部也制约着整体,甚至在一定条件下关键部分的性能对整体起决定作用.该题在解答过程中将这种思想进行了很好的渗透,在利用函数奇偶性排除选项时,利用了奇偶性是函数整体性质的特点,而函数在特定点周边的变化趋势则是局部特点,两者有效结合,给解题带来便捷.同时也深层次的引导青年学生在思考问题时要有全局的大方向把握,也要有细致到点的缜密分析,方能做出正确的决策.

2.3 “动与静”的辩证思维

例3(2020 全国一卷理20)已知A,B分别为椭圆y2=1(a ＞1)的左、右顶点,G为E的上顶点,P为直线x=6 上的动点,PA与E的另一交点为C,PB与E的另一交点为D.

(1)求E的方程;

(2)证明:直线CD过定点.

评注按照马克思主义物质观:运动作为物质的存在形式、固有属性和根本属性,是指宇宙间所发生的一切变化和过程;静止是指相对某一参照系,事物没有发生特定的变化或者事物的根本性质不变.该题在命制过程中,第一问问的是椭圆的标准方程,这是固定的,唯一的,可以理解为静;第二问问的是直线恒过定点问题,但是直线CD上的两个点C,D是会运动的,然而却又经过的定点,此时依托于第一问将动与静的结合推向了高潮,将动与静的美感提升了一个层次,在考查学生圆锥曲线知识的同时,引领学生对哲学的动静的思考,感受试题中的哲学辩证美学意义.

2.4 “联系与发展”的辩证思维

例4(2020年全国1 卷理3)埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( )

评注马克思主义辩证法认为:联系和发展是紧密相连、不可分割的辩证统一关系.本题以国外著名建筑金字塔为命题背景,结合立体几何的相关知识点对学生进行考察,题目难度不大.其命题意图是想让考生在做题过程中不知不觉的感受国外的古代数学的灿烂与辉煌,让考生在取得数学知识的同时,开阔眼界,具有很好的人文价值,另一方面学生容易联想到国内的“万里长城”、“乐山大佛”、“北京故宫”等中国古代建筑奇迹,渗透培养学生的爱国主义情操.

2.5 “对立与统一”的哲学思维

例5(2013 陕西理17)设{an}是公比为q的等比数列.(1)推导{an}的前n项和公式;(2)设q /=1,证明数列{an+1}不是等比数列.

解(1)当q=1 时,Sn=a1+a1+...+a1=na1;当q /=1 时,

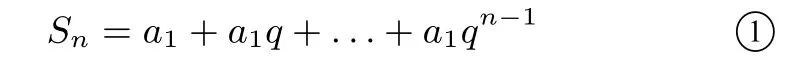
评注对立统一规律揭示了客观存在具有的特点,任何事物内部都是矛盾的统一体,矛盾是事物发展变化的源泉、动力.本题基于考查等比数列得原始概念,强调运用定义处理问题,正面直接证明数列{an+1}不为1 的公比相对比较有难度,我们转而利用找出对立面,结合前面所提及的公比去发现矛盾,进而逆向证明该命题的正确性,也引导我们在处理很多问题时候,可以从对立面入手,很多时候会有意想不到的收获.

2.6 “量变与质变”的辩证思维

3 教学启示

在高中数学教学中应用发展与联系的眼光看待知识,寻找各部分知识的内在联系.在教会学生数学知识的同时应加大思想层次的拔高,仔细品读各高考纲领性文件,例如《课标2020 修订版》《中国高考评价体系》等等,无一不是首先强调思想上的引领.所以我们的教学也要符合哲学思想,不能微观地只关心学生的成绩,而要宏观地全面地看到学生的整体情况,切实做到传授科学知识时候体现科学价值也要体现人文价值,感受辩证美学,做到所授内容对其未来发展有所帮助.