一种改进蚁群算法的移动机器人路径规划算法

沈葭栎，李燕，2，季建楠，佘宇

（1.南京信息工程大学，自动化学院，南京210044；2.南京信息工程大学滨江学院，物联网学院，无锡214105）

0 引言

移动机器人的路径规划在机器人技术中尤为重要。移动机器人可通过人类的设计规划，替代人类进行危险复杂的工作。移动机器人路径规划常用的算法有Dijkstra算法［1］、A*算法［2］、人工势场法［3］等。在较多障碍物的情况下，仿生智能算法能够帮助移动机器人寻找到较优路径。近年来一些学者通过粒子群算法［4］、遗传算法［5］、DNA计算［6］、蚁群算法等来解决机器人路径规划问题。

Marco Dorigo于1992年在他的博士论文中提出蚁群算法，是一种启发式全局优化算法。蚁群算法具有正反馈、并行性，易与其他算法相结合的优点［7］。但传统蚁群算法存在收敛速度慢，易陷入局部最优等问题。近年来一些学者提出了一些改进的蚁群算法。2014年杜鹏桢等人提出一种面向对象的多角色蚁群算法，对蚁群结构进行优化分为分工不同地三种蚁群，仅各蚁群最优个体进行信息素更新，对于大规模TSP问题有较好的结果［8］。2020年杜玉红等人提出了一种粒子群参数优化的改进蚁群算法，实验结果表明改进算法可提高移动机器人到达目标点的速度并降低机器人运动过程中的损耗［9］。2020年官娟等人提出一种基于MIMIC算法和RPCA的混合蚁群算法，通过实验对比表明在连续域上寻优能力和收敛性方面都有明显的提高［10］。

研究机器人路径规划问题可分为两部分。第一部分是机器人运动环境的搭建，将机器人的运动空间解析成机器人能识别的数学模型，在机器人全局路径规划问题中，栅格法是最常用的环境建模方法。第二部分是路径规划方法的选择。为解决蚁群算法收敛慢，易陷入局部最优解的问题。本文提出一种对蚁群算法中信息素的更新进行改进的方法，引入了惩罚系数的概念，使当前最优路径上的信息素浓度下降，从而达到跳出局部最优的目的。将信息素浓度设置为分级动态变化，随迭代次数增加而逐渐衰减，当迭代到一定次数后，不再衰减，达到加速收敛的目的。

1 环境建模

栅格法是将机器人的工作环境建立在二维直角坐标系上，根据机器人运动空间的实际情况，将地图分割成固定大小的栅格。栅格环境为X行Y列，每个栅格边长都为1。栅格地图内的可分为三种栅格：第一种是障碍栅格，第二种是可移动栅格，第三种是起始点栅格。

起点坐标为（0，0），终点坐标为（19，19）。在本文中蚂蚁只能朝上、下、左、右、左上、右上、左下、右下八个方向运动。栅格地图如图1所示，其中黑色为障碍物。

图1 栅格地图

2 传统蚁群算法（AS）

以旅行商（TSP）问题为例，将m只蚂蚁放入有n个城市的环境中，当t时刻，随机选取一个城市i，让第k只蚂蚁从该城市出发，以公式（1）计算得到的概率采取蒙特卡洛算法来选择这只蚂蚁下一个到达的城市。

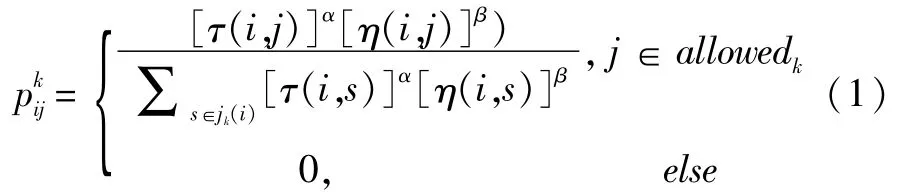
每个蚂蚁在搜素的过程中，会在已走过的路径上留下一定浓度的信息素，加大整个系统的正反馈，使算法加速收敛。AS的信息素更新有三种模型：①蚁周模型；②蚁量模型；③蚁密模型。蚁周模型是使用比较多的一种，信息素更新方式见公式（2）。

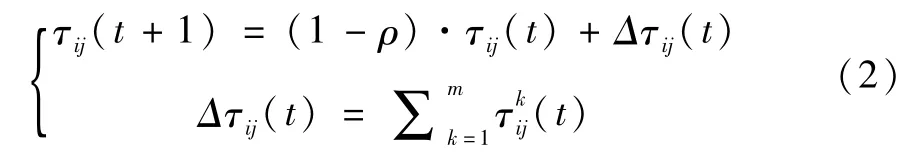
公式（2）中：ρ是信息素挥发因子，表示信息素的持久度，该系数增大会使之前蚂蚁在路径上留下的信息素挥发变快，导致算法随机性加强，收敛速度也降低了；反之，该系数的减小会使之前遗留在路径上的信息素挥发减慢，能够加速算法的收敛，也会导致算法陷入局部最优的情况。Δτij是蚂蚁搜索完成后，在路径上留下的信息素增量，要与之前地图中的信息素进行叠加。在达到设定的迭代次数，或得到期望的解时，结束整个过程，输出最优解。

3 改进蚁群算法

3.1 优化路径搜索策略

（1）后退策略。蚂蚁在路径搜索的过程中将蚂蚁已经走过的路径节点存入禁忌表，禁忌表中已有节点在选择下一个节点时不会被选取，当蚂蚁进入U型障碍会使蚂蚁找不到可选择的下一节点，如图2所示。

图2 U型障碍

针对U型障碍会使蚂蚁找不到可选择的下一节点，或其他找不到可选择的下一节点的问题，引入后退策略。蚂蚁沿着原路径返回，每后退一个节点，判断是否有未走过的节点，如果找到了就走新的节点，更新禁忌表中已走过节点，继续算法的进行。

（2）修正策略。除了上述无法找到可选择的下一节点的问题。在搜索过程中，因为路径信息素浓度的影响，蚂蚁在路径选择大概率选择信息素浓度高的节点从而出现了绕路，会存在两种路径缺陷，如图3和图4所示。

图3 路径缺陷1

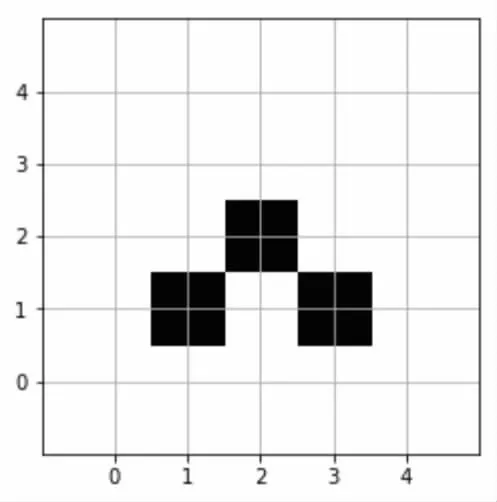
图4 路径缺陷2

在每次迭代结束后，对迭代的最优路径进行分析，判断是否存在路径缺陷问题，并通过修正策略进行修正，修正后的路径就是此次迭代的最优路径。路径修正如图5和图6所示。

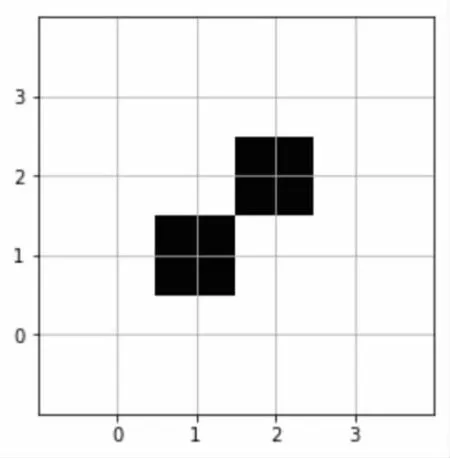
图5 修正后路径缺陷1

图6 修正后路径缺陷2

3.2 动态分级信息素浓度

在传统蚁群算法中，如果使用的是蚁周模型，信息素的更新都取决于上一次迭代中的结果最好的一次，影响信息素的更新，其中求解质量较差的路径就会影响算法后续迭代的解的质量，导致算法收敛速度变慢。为降低质量较差的迭代结果对算法的负优化，提高质量较高的迭代结果对算法的影响，引入了信息素浓度的分级策略。根据栅格地图大小，设定每个级别的路径长度界限，将每次迭代的结果分为：优质路径，信息素浓度为Q1；较优路径，信息素浓度Q2；较差路径，信息素浓度Q3；低质路径，信息素浓度为Q4。

在传统蚁群算法中，信息素浓度Q和挥发系数ρ的值对于整个算法的收敛速度是起决定作用的。Q的值偏大，而挥发系数ρ的值偏小时，算法容易陷入局部最优。而Q的值偏小，挥发系数ρ的值偏大时，算法整体的全局搜索能力变得极低。针对这一问题，提出一种动态变化信息素浓度Q的方式，随着迭代次数的增加，逐渐降低各级信息素浓度，达到设定好的迭代次数时，停止信息素浓度的衰减，此时Q的值固定为常量，后续的迭代Q的值不再发生变化。动态衰减信息素浓度的策略，可以使算法在初期获得较快收敛速度，逐渐降低的信息素浓度可以保证算法不陷入局部最优问题。

结合以上两点改进的动态分级信息素浓度Q的设置如下，见公式（3）。

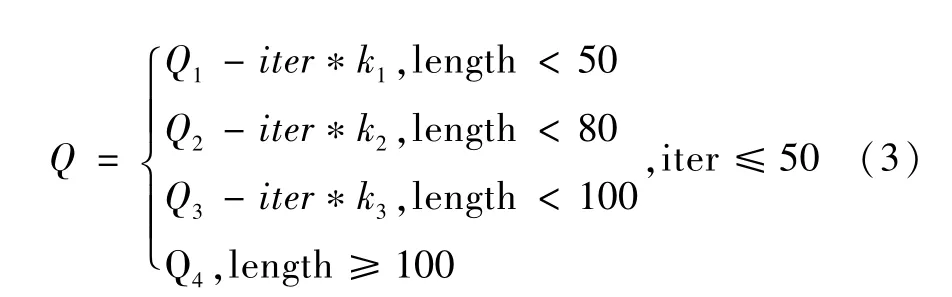
公式（3）中：Q1、Q2、Q3、Q4分别是各级信息素浓度的初始值；length是每代的最短路径；iter是迭代的次数；k1、k2、k3是每次迭代后各级信息素浓度的衰减系数。当迭代次数超过50次后，信息素浓度Q就为固定值。

这种方式，达到了加快收敛速度的目的，也能避免因为信息素浓度突然增加，导致算法容易陷入局部最优的情况。

3.3 引入惩罚系数

当算法迭代多次以后，相对优秀的路径上的信息素浓度会远高于其他较差的路径上的浓度，使算法随机性大大降低，不利于寻找更优的路径。为解决这一问题，引入了惩罚系数ε，当算法迭代到K代以后，判断当前最优路径L代未发生变化，下一次更新信息素时，将当前最优路径上的信息素浓度衰减。信息素衰减公式，如公式（4）所示。

3.4 蚁群算法相关参数

蚁群算法中，参数的选取影响收敛速度和寻优结果，主要涉及的参数有蚂蚁数量、信息素挥发系数ρ、信息素启发因子α与期望启发因子β、迭代次数。具体分析如下：

（1）蚁群大小。蚁群大小直接影响搜索效率，蚁群数量过小，无法遍历全地图获取全局最优路径。

（2）挥发系数。信息素是蚂蚁在走过的路径上留下的信息量之和，影响后面蚂蚁的路径选择。随着算法的迭代，路径上的信息素会挥发。信息素挥发系数对收敛速度和寻优能力起主要影响。挥发系数变大，算法的收敛速度加快，搜索能力降低；挥发系数减小，算法收敛速度减慢，搜索能力提高。

（3）信息素启发因子α与期望启发因子β。信息素启发因子表示信息素浓度对选择路径的影响大小；期望启发因子表示路径长度对路径选择的影响。α影响蚁群选择之前走过路径的概率，β影响算法的搜索效率。

（4）迭代次数。迭代次数过小，会导致算法提前结束，求解结果不理想。迭代次数过大会使算法效率降低，影响求解速度。

4 实验仿真与分析

基于以上分析，在20×20的栅格地图中进行实验仿真分析。对于本文算法公式中出现的参数进行赋值：每一次迭代蚂蚁的数量M为50只；最大迭代次数为100次；信息素启发因子α为1，期望启发因子β为7；信息素挥发系数ρ为0.3；动态分级信息素浓度Q中，Q1、Q2、Q3、Q4分别为2.5、2、1.5、1；启用惩罚系数的迭代次数K为30，最优路径连续未改变的次数L为5次，惩罚系数ε为2。仿真结果如图7所示。

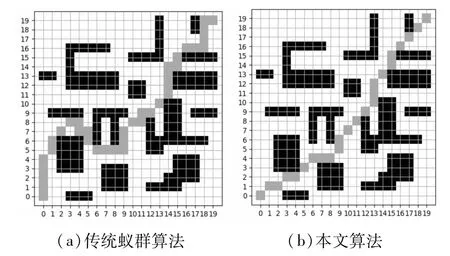
图7 两种蚁群算法仿真结果

表1记录了传统蚁群算法和本文算法最优路径长度，以及第一次出现最优路径的迭代次数，来进行比较。

表1 算法对比

从仿真结果来看，两种蚁群算法都能对路径进行规划，但与传统蚁群算法相比，本文算法具有更强的路径规划能力，在路径长度上有较强的优化效果。

从图8两种蚁群算法的收敛曲线来看，与传统蚁群算法相比，本文算法具有更快的收敛速度，对于迭代次数也有很好的优化能力。

图8 两种蚁群算法收敛曲线

5 结语

本文针对移动机器人路径规划问题，提出了一种改进的蚁群算法。将传统蚁群算法中固定的信息素浓度，改进为动态分级的信息素浓度，达到了加速收敛的目的。引入了后退策略来避免蚂蚁陷入死锁导致的算法失效。通过修正策略，对蚂蚁搜索路径过程中存在的一些路径行为进行修正，缩短了路径距离。通过设置惩罚函数，来提高提高算法运行到中后期的随机性避免陷入局部最优，影响算法的搜索结果。仿真数据显示：本文所提出的改进的蚁群算法，在路径长度的优化以及迭代次数的优化方面都具有不错的效果，具有良好的全局搜索效果。