感潮河段上游洪水与河口潮位遭遇研究

彭慧 刘璐 姜钧耀 孟含威 王翊人 李光吉

摘 要：采用定性分析和定量计算相结合的方法研究洪水与潮位遭遇，首先采用定性分析法确定洪水与潮位遭遇可行方案集，再利用洪水与潮位遭遇的组合风险概率模型定量计算各种可行方案集的风险率，统筹考虑防洪安全及工程投资，最终确定洪水与潮位遭遇最优方案。以小清河为例的研究表明：洪潮遭遇可行方案集为50 a一遇洪水遭遇5～50 a一遇潮位，最优组合为50 a一遇洪水遭遇20 a一遇潮位;潮洪遭遇可行方案集为50 a一遇潮位遭遇3～140 a一遇洪水，最优组合为50 a一遇潮位遭遇20 a一遇洪水;超标准洪水遭遇高潮潮位的发生风险较低，高潮位遭遇中小洪水的发生风险较高。

关键词：洪水与潮位遭遇;定性分析;Copula 函数;组合风险率模型;小清河

中图分类号：P333 文献标志码：A

doi：10.3969/j.issn.1000-1379.2021.08.008

引用格式：彭慧，刘璐，姜钧耀，等.感潮河段上游洪水与河口潮位遭遇研究[J].人民黄河，2021，43（8）：44-47.

Abstract： The qualitative analysis and quantitative calculation were put forward to obtain the reasonableencounter scheme between floods and tides. First the qualitative analysis was used to obtain the feasible schemes. Then the probabilistic models were built based on Copula function. Finally the optimal scheme was adopted by balancing the safety and investment. The application of Xiaoqinghe River illustrates that the optimal schemes are 50-year floods encountering 20-year tides and 50-year tides encountering 20-year floods. Using the two schemes to analyze water level respectively， the maximum levels are used to river regulation design. Moreover， the typical year analysis results show that the risk of excess criteria floods encountering tides is infrequent and the risk of excess tides encountering criteria floods is frequent.

Key words： encounter between floods and tides; qualitative analysis; Copula function; probabilistic models; Xiaoqinghe River

1 引 言

感潮河段水位受上游洪水和下游潮位顶托双重影响，在防洪除涝工程设计中，合理确定洪水与潮位遭遇是首先需要解决的问题[1]。目前洪水与潮位遭遇的研究主要集中在风险分析领域。刘曾美等[2-3]提出组合风险率模型来定量研究洪潮遭遇风险率;曾强等[4]针对感潮河段实测流量资料缺乏问题，采用降水资料代替流量资料，提出治涝风险、同现风险和组合风险并进行洪水与潮位遭遇分析。

洪水与潮位相关性较弱[2]，二者遭遇通常有多种情况，已有研究大多凭经验设定遭遇方案。然而，近年来极端天气呈现增多增强趋势，超标准洪水与高潮位遭遇频率增大。山东省小清河流域2019年受利奇马台风暴雨影响，遭受了140 a一遇洪水与50 a一遇高潮潮位组合，受潮汐顶托影响，洪水排泄不畅，发生了严重洪涝灾害。因此，进行遭遇分析时考虑极端洪水与潮位组合，将更有利于防洪安全。本文以确定小清河感潮河段洪潮遭遇（洪水为主，潮位相应）、潮洪遭遇（潮位为主，洪水相应）为研究目的，首先利用历年洪水与潮位同步观测资料，分别绘制实测洪潮遭遇散点图和实测潮洪遭遇散点图，以接近设计降水量年份发生的各种潮位作为洪潮遭遇可行方案集，以接近设计潮位年份发生的各种降水量作为潮洪遭遇可行性方案集，其次利用组合风险率模型定量分析各可行方案集的风险率，再统筹考虑防洪安全及工程投资，最终确定最优洪水与潮位遭遇组合，以期为感潮河道规划设计提供决策依据。

2 洪水与潮位遭遇的风险分析模型构建及求解

2.1 联合分布函数

实测大暴雨洪水统计资料分析表明，通常最大1 d降水量对洪峰起主要作用，故利用最大1 d降水量代替洪峰流量进行洪水与潮位遭遇分析。令年最大1 d 降水量为q，z为年汛期最高高潮位，F（z）、F（q）为边缘分布函数，C（q，z）为洪潮联合分布函数，C（z，q）为潮洪聯合分布函数，根据Sklar定理[5]，一定会存在唯一的二维Copula 函数θ1、θ2，使得

2.2 风险分析模型构建

工程设计更关注洪水与潮位两个随机变量中至少一个变量超设计值的情形[2，6]。令P（z>zd，q≤qd）表示河道发生不超过设计标准洪水qd而河口发生超过设计标准潮位zd的概率。此概率表明即使洪水不超标准但仍可能受灾的风险，洪潮组合风险率用R（q，z）表示。

风险率愈小愈安全，但会造成工程设计标准偏高，不经济，因此需要在防洪安全与工程投资之间寻求平衡点，选定适当的风险率，从而确定洪水与潮位遭遇组合。

2.3 风险分析模型求解

Copula函数总体上可分为三类：椭圆型、Archimedean型和二次型。水文上常用的Gumbel-Hougard （GH） Copula、Clayton Copula及Ali-Mikhail-Haq （AMH） Copula均属于Archimedean Copula[5]。Kendall秩相关系数τ常被用于描述水文变量间的相关性。三种Copula函数的适用范围、τ与θ之间的关系如下。

（1）GH Copula函数：适用于具有正相关关系的随机变量。

（2）Clayton Copula函数：适用于具有正相关关系的随机变量。

（3）AMH Copula函数：适用于相关性较弱，具有正、负相关关系的随机变量。

式中：C（u，v） 为联合分布函数;u和v为边缘分布函数的参数;θ为Copula函数的参数。

通常可采用离差平方和最小准则来择优选取Copula函数，其公式为

3 实例研究

3.1 研究区概况

小清河位于山东省鲁北平原南部，全长229 km，流域面积10 433 km2，流向大致与黄河平行，自西向东流入渤海莱州湾。入海口位于渤海莱州湾南岸，沿海天文潮汐属“一日两潮”的不规则半日潮海区，下游建有王道闸拦潮水（见图1）。王道闸至入海口河段长29.5 km，流域面积3 358 km2。干流入海口建有羊角沟潮位站，有1951—2019年实测潮位观测资料，汛期最高高潮位均值2.03 m，最大值3.54 m，最小值1.53 m。全流域雨量站有1951—2019年实测暴雨资料，雨量站分布见图2。

3.2 資料选样

根据历年降水与潮位的同步观测资料，进行年最大1 d 降水量q和相应年汛期最高潮位z资料选样时，很多年份二者并不是刚好发生在同一时间。本文在年最大1 d降水量发生日前后滑动1 d，然后在该时段选取潮位最大值作为相应潮位。同理，在年汛期最高高潮位发生日前后滑动1 d，然后在该时段选取1 d降水量最大值作为相应最大1 d降水量。

3.3 洪水与潮位遭遇可行方案集

小清河防洪除涝工程设计标准为50 a一遇。

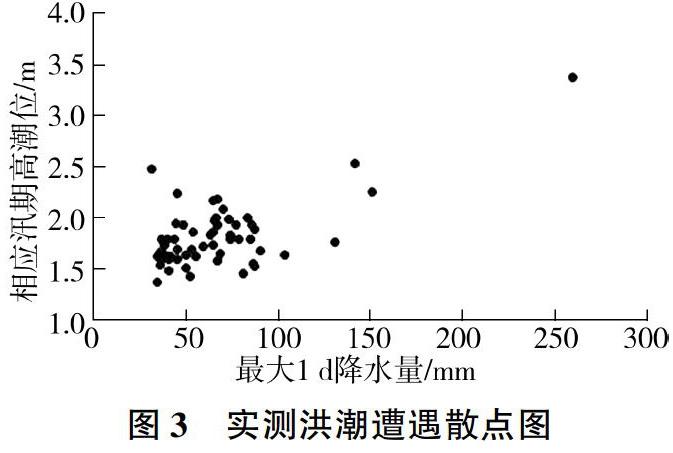
（1）洪潮遭遇分析。50 a一遇最大1 d降水量为158.3 mm，利用实测洪潮遭遇散点图（见图3），汛期最高高潮位可能为2.53、2.25、1.76 m，重现期为5～10 a。考虑防洪安全，本次确定洪潮遭遇方案集为50 a一遇洪水遭遇5～50 a一遇潮位。

（2）潮洪遭遇分析。50 a一遇汛期最高高潮位为3.38 m，利用实测潮洪遭遇散点图（见图4），最大1 d降水量可能为68.9、259.8 mm，重现期为3～140 a。由此确定潮洪遭遇方案集为50 a一遇潮位遭遇3～140 a一遇洪水。

3.4 洪水与潮位遭遇风险率

3.4.1 边缘分布参数

对历年实测最大1 d降水量、汛期最高潮位进行频率分析，频率曲线采用P-Ⅲ型曲线，曲线参数采用矩法估计初值，再采用目适法以理论频率分布曲线与经验点据拟合较好为原则来优选参数，各水文变量边缘分布的参数估计成果见表1。

3.4.2 洪潮遭遇风险率计算及结果分析

（1）联合分布函数。经计算洪潮遭遇的Kendall秩相关系数τ1=0.24。GH Copula、Clayton Copula、AMH Copula 三种函数的θ及OLS见表2。根据OLS最小准则，选取Clayton Copula为洪潮联合分布函数。

（2）洪潮遭遇风险率。由表3可知50 a一遇洪水遭遇10、5 a一遇潮位风险率接近或超过10%，相对不安全;遭遇50、20 a一遇潮位风险率分别为1.90%、4.77%。感潮段防洪工程按50 a一遇洪水遭遇50 a一遇潮位设计，投资为35.9亿元;按50 a一遇洪水遭遇20 a一遇潮位设计，投资为21.3亿元。综合考虑防洪安全与工程投资，推荐洪潮组合为50 a一遇洪水遭遇20 a一遇潮位。

（3）典型台风暴雨洪潮遭遇风险率。2019年“利奇马”台风暴雨重现期为140 a，汛期最高高潮位重现期为50 a，利奇马台风暴雨洪潮遭遇风险率为1.97%，说明小清河流域超标准洪水遭遇高潮潮位发生概率较低。

3.4.3 潮洪遭遇风险率计算及结果分析

（1）联合分布函数。潮洪遭遇Kendall秩相关系数τ2=0.062。根据OLS最小准则，选取AMH Copula为潮洪联合分布函数。

（2）潮洪遭遇风险率。由表4可知50 a一遇潮位遭遇3.3 a一遇潮洪水风险率超过10%，相对不安全;遭遇140、50、20 a一遇洪水风险率分别为0.70%、1.99%、4.98%。综合考虑防洪安全与工程投资，推荐潮洪组合为50 a一遇潮位遭遇20 a一遇洪水。

（3）典型台风暴雨潮洪遭遇风险率。1992年台风暴雨汛期最高高潮位3.54 m，为羊角沟站实测潮位最大值，重现期63 a，遭遇暴雨重现期3.4 a，潮洪遭遇风险率为29.27%，说明小清河流域高潮位遭遇中小洪水概率是较高的。

4 结 论

（1）利用洪水与潮位同步观测资料所确定的洪潮遭遇、潮洪遭遇可行性方案集，符合流域洪水与潮位遭遇特性。

（2）利用Copula函数构建洪潮遭遇和潮洪遭遇的组合风险率模型，可定量计算洪水与潮位两个随机变量中至少一个变量超设计值的情形，切合工程规划设计实际。

（3）对小清河而言，分别采用50 a一遇洪水遭遇20 a一遇潮位、50 a一遇潮位遭遇20 a一遇洪水两种洪水与潮位组合方案推求水面线，两方案外包线作为感潮段50 a一遇设计水面线。同时，根据实测超标准洪水及高潮潮位资料分析，超标准洪水遭遇高潮潮位的风险较低，高潮位遭遇中小洪水的风险较高。

参考文献：

[1] 童汉毅，赵明登，槐文信，等.洪潮遭遇情况的水动力学计算[J].武汉水利电力大学学报，2000，33（5）：11-15.

[2] 刘曾美，陈子燊，李粤安.感潮河段洪潮遭遇组合风险研究[J].中山大学学报（自然科学版），2010，49（2）：113-118.

[3] 刘曾美，覃光华，陈子燊，等.感潮河段水位与上游洪水和河口潮位的关联性研究[J].水利学报，2013，44（11）： 1278-1285.

[4] 曾强，董晓华，刘冀，等.基于Copula函数的感潮河段洪潮遭遇组合风险分析研究[J].水文，2019，39（2）：1-6.

[5] 郭生练，闫宝伟，肖义，等.Copula函数在多变量水文分析计算中的应用及研究进展[J].水文，2008，28（3）：1-7.

[6] 李世举，周建伟，白领群.感潮河段潮洪组合设计水位计算方法研究[J].人民黄河，2006，28（10）：33-34.

【责任编辑 许立新】